小升初复习精讲精练专题三《数与方程》--人教版(复习课件)(共25张PPT)
文档属性
| 名称 | 小升初复习精讲精练专题三《数与方程》--人教版(复习课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
专题三:数与方程
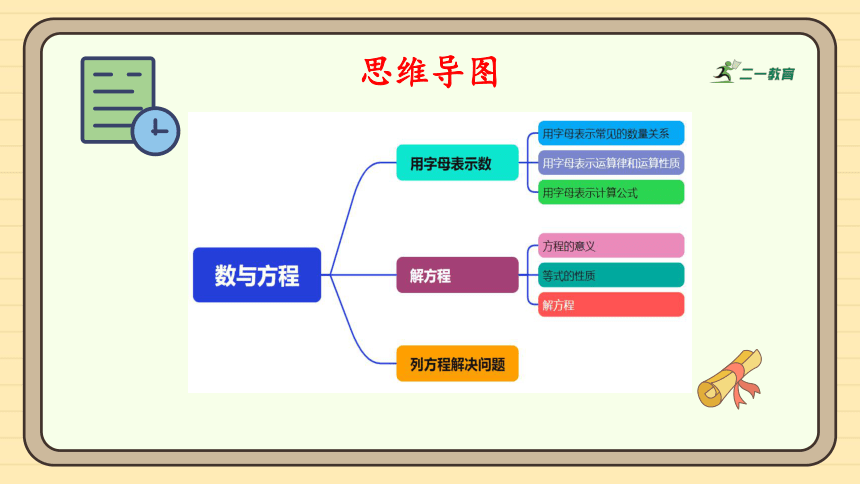
思维导图
01
用字母表示数
知识清单
1、用字母表示常见的数量关系
①路程(s)、速度(v)、时间(t)三者之间的关系:s=vt
②总价(a)、单价(b)、数量(c)三者之间的关系:a=bc b=a÷c c=a÷b
2、用字母表示运算律和运算性质
(1)运算律
加法交换律:a+b=b+a 加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:a×(b+c)=a×b+a×c
(2)运算性质
减法性质:a-(b+c)=a-b-c a+(b-c)=a+b-c a-(b-c)=a-b+c
除法性质:a÷(b×c)=a÷b÷c
01
用字母表示数
知识清单
3、用字母表示计算公式
(1)周长
长方形:C=2(a+b)
正方形:C=4a
圆:C=2πr=πd
(3)表面积
长方体:S=2(ab+ah+bh)
正方体:S=6a
圆柱:S=2πrh+2πr
(2)面积
长方形:S=ab
正方形:S=a
平行四边形:S=ah
三角形:S=ah÷2
梯形:S=(a+b)h÷2
圆:S=πr
(4)体积
长方体:V=abh
正方体:V=a
圆柱:V=Sh
圆锥:
02
解方程
知识清单
1、方程的意义:根据等量关系列出的含有未知数的等式叫作方程。
2、等式的性质
①等式两边同时加上或减去相同的数,所得结果仍然是等式
②等式两边同时乘或除以一个相同的数(0除外),所得结果仍然是等式
02
解方程
知识清单
3、解方程
①方程的解:使方程左右两边相等的未知数的值叫作方程的解。
举例:x=3是方程8x=24的解
②解方程:求方程中未知数的值的过程叫作解方程。
03
列方程解决问题
知识清单
1.列方程解应用题步骤
①根据题意,确定未知数,并用x (或其他字母)表示
②找数量间的相等关系(画图、根据公式、根据关键句、根据常见的数量关系)
③列方程
④解方程
⑤检验并写出答案
04
题型训练
例题精讲
01 用字母表示数
1.用小棒摆五边形,如图:按这个规律,摆n个五边形,需要( )根小棒;照这样摆,用97根小棒能摆( )个五边形。
【答案】4n+1 24
【解答】5+4×(n-1)
=5+4n-4
=(4n+1)根
(97-1)÷4
=96÷4
=24(个)
用小棒摆五边形,如图:按这个规律,摆n个五边形,需要(4n+1)根小棒;照这样摆,用97根小棒能摆24个五边形。
04
题型训练
例题精讲
01 用字母表示数
2.每张课桌的价钱是m元,椅子比课桌便宜30元,那么m-30表示的是( ),m+(m―30)表示( ),如果2张桌子和4把椅子的价格相等,将这一关系用含有字母的等式表示出来是( )。
【答案】一把椅子的价钱 一把椅子和一张桌子的总价钱 2m=4(m-30)
【解答】每张椅子比课桌便宜30元,即每张椅子=每张课桌的价钱-30=m-30。
m+(m―30),其中m表示每张课桌的价钱,(m-30)表示每张椅子的价钱,因此m+(m―30)表示一张椅子和一张桌子的总价钱。
2张桌子的价钱表示为2m,4把椅子的价钱表示为4(m-30),2张桌子和4把椅子的价格相等,即2m=4(m-30)。
因此m-30表示的是一张椅子的价钱;m+(m―30)表示一张椅子和一张桌子的总价钱;如果2张桌子和4把椅子的价格相等,将这一关系用含有字母的等式表示出来是2m=4(m-30)。
04
题型训练
例题精讲
02 解方程
1.解方程。
【答案】x=15;x=3
【解答】(1)x÷1.5=10
解:x÷1.5×1.5=10×1.5
x=15
(2)0.4x+0.6×2.5=2.7
解:0.4x+1.5=2.7
0.4x+1.5-1.5=2.7-1.5
0.4x=1.2
0.4x÷0.4=1.2÷0.4
x=3
04
题型训练
例题精讲
02 解方程
2.在天平的“?”处添加下列物品后,天平不能保持平衡的是( )。
A. B. C. D.
【答案】A
【解答】A.天平右端原有2个正方体,再添加 6个正方体,则右端有2+6=8个正方体,天平不能保持平衡;
B.天平右端原有2个正方体,再添加 ,相当于添加2+2=4个正方体,则右端有2+4=6个正方体,天平能保持平衡;
C.天平右端原有2个正方体,再添加 ,相当于添加2+2=4个正方体,则右端有2+4=6个正方体,天平能保持平衡;
D.天平右端原有2个正方体,再添加 4个正方体,则右端有2+4=6个正方体,天平能保持平衡。 故答案为:A
04
题型训练
例题精讲
03 列方程解决问题
1.一队少先队员乘船过河,如果每船坐15人,还剩9人;如果每船坐18人,刚好剩余1只船。共有多少只船?(用方程解答)
【答案】9只
【解答】解:设共有x只船。
15x+9=(x-1)×18
15x+9=18x-18
15x+9-15x=18x-18-15x
9=3x-18
3x-18+18=9+18
3x=27
3x÷3=27÷3
x=9 答:共有9只船。
04
题型训练
例题精讲
03 列方程解决问题
2.如图,大长方形由9个正方形组成,已知中间最小的正方形边长为1厘米,求大长方形的周长。
【答案】C
【解答】解:设右上角的正方形边长为x厘米,则9个正方形的边长从小到大依次是1、x、2x、2x+1、2x+2、2x+3。
x+x+2x+2x+1=2x+3+2x+2
6x+1=4x+5
6x-4x=5-1
2x=4
x=4÷2
x=2
长:2×2+1+2×2+2+2
=13(厘米)
2×2+1+2×2+2
=11(厘米)
(13+11)×2
=24×2
=48(厘米)
答:大长方形的周长是48厘米。
05
专项训练
专项练习
1.食堂买来a袋大米,每袋25千克,已经吃了b千克,还剩( )千克;当a=20,b=375时,则还剩( )千克。
2.一张长方形的纸,剪去一个长acm、宽3cm的长方形以后就变成了一个正方形(如图),则原来长方形的周长是( )cm,面积是( )cm2。
25a-b
a2+3a
4a+6
125
05
专项训练
专项练习
3.a是一个不为0的数,当a=( )时,a2=2a;当a<2时,a2( )2a。
4.下面这些式子中,等式有( ),方程有( )。(填序号)
①x-30=26 ②25×2=50 ③6+m ④ 5a<2.5 ⑤ x÷0.3=1.2
2
①②⑤
①⑤
<
05
专项训练
专项练习
5.根据题意写出等量关系式,再列方程。
冬冬看一本360页的书,他每天看x页,看了5天后还剩45页没有看。
(1)( )-( )=( )
方程: 。
(2)( )+( )=( )
方程: 。
6.一个两位数,十位上的数字是a,个位上的数字是b,这个两位数用含有字母的式子表示是( )。
A.ab B.10a+b C.10b+a D.10(a+b)
书的总页数
已经看的页数
剩下没看的页数
360-5x=45
已经看的页数
剩下没看的页数
书的总页数
5x+45=360或45+5x=360
B
05
专项训练
专项练习
7.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出4千克放入乙袋,那么甲、乙两袋质量相等。列成等式是( )。
A.a+4=b-4 B.a-b=4 C.(a+b)÷2=4 D.a-4=b+4
8.六年级两个班上交的绘画作品情况如图所示,下列等量关系错误的是( )。
A. x B. C.
B
D
05
专项训练
专项练习
9.下列选项中,不能用方程“x+3x=44”来解释的是( )。
A.
B.
C.一个长方形周长是44dm。长为3x dm,宽为x dm。
D.全班有44人,其中男生有x人,女生是男生的3倍。
10.一个足球的表面由一些黑色五边形和白色六边形组成,如下图所示,每个五边形周围有5个六边形,每个六边形周围有3个五边形。已知五边形的总数是12,那么六边形的总数是( )。
A.20 B.30 C.40 D.50
C
A
05
专项训练
专项练习
11.爸爸、哥哥、妹妹三人现在的年龄和是64岁,当爸爸的年龄是哥哥年龄的3倍时,妹妹是9岁。当哥哥的年龄是妹妹年龄的2倍时,爸爸是34岁。现在哥哥的年龄是几岁?
解:设哥哥年龄是x岁,那么爸爸是3x岁。
3x-x=34-2×(x-9)
2x=34-2x+18
4x=52
x=52÷4
x=13
哥哥与妹妹年龄差为:13-9=4(岁)
此时爸爸年龄为:13×3=39(岁)
爸爸与哥哥的年龄差为:39-13=26(岁)
64-26+4
=38+4
=42(岁)
现在哥哥年龄:42÷3=14(岁)
答:现在哥哥14岁。
05
专项训练
专项练习
12.蟋蟀的鸣叫是大自然的音乐,并且蟋蟀鸣叫的频率与气温有着很大的关系。人们发现某地某种蟋蟀每分钟鸣叫的次数和气温之间有以下的关系:用蟋蟀1分钟鸣叫的次数除以7,再加上3,结果等于该地当时的气温(单位℃)。
(1)如果用T表示该地当时的气温,m表示蟋蟀每分钟鸣叫的次数,请用含有字母的式子表示T和m的关系。
(2)当m=203时,该地当时的气温是多少摄氏度?
(1)T=m÷7+3
答:用含有字母的式子表示T和m的关系为:T=m÷7+3。
(2)203÷7+3
=29+3
=32(摄氏度)
答:该地当时的气温是32摄氏度。
05
专项训练
专项练习
13.某市出租车收费标准如下:3千米以内(含3千米)收8元,超过3千米的部分,每千米收2.4元。张叔叔坐出租车从体育馆到火车站一共行了b(b>3)千米。
(1)用含有字母的式子,表示张叔叔坐出租车从体育馆到火车站,一共花了多少钱?
(2)当b=10时,张叔叔坐出租车从体育馆到火车站一共花了多少钱?
(1)行驶3千米的费用:8元;
超过3千米部分的费用:[2.4×(b-3)]元;
一共:8+2.4×(b-3)
=8+2.4×b-2.4×3
=(2.4b+0.8)元
答:张叔叔坐出租车从体育馆到火车站,一共花(2.4b+0.8)元。
(2)当b=10时
2.4b+0.8
=10×2.4+0.8
=24+0.8
=24.8(元)
答:当b=10时,张叔叔坐出租车从体育馆到火车站一共花了24.8元。
05
专项训练
专项练习
14.供水公司为了鼓励居民节约用水,规定:每户每月用水不超过5立方米时,按每立方米1.6元收费;超过5立方米的部分按每立方米4元收费。王丽家5月份平均每立方米水费是2.5元,请你算一算,王丽家5月份共交水费多少元?
解:设王丽家5月份用水x立方米。
5×1.6+(x-5)×4=2.5x
8+4x-20=2.5x
8+4x-20+20-8=2.5x+20-8
4x =2.5x+12
4x-2.5x =2.5x+12-2.5x
1.5x=12
1.5x÷1.5=12÷1.5
x=8
2.5×8=20(元)
答:王丽家5月份共交水费20元。
05
专项训练
专项练习
15.甲乙两车从相距360千米的A,B两地同时出发相向而行,甲车的速度是乙车的1.4倍,2小时后相遇。求乙车的速度?
解:设乙车的速度是x千米/时,则甲车的速度是1.4x千米/时。
(x+1.4x)×2=360
2.4x×2=360
2.4x×2÷2=360÷2
2.4x=180
2.4x÷2.4=180÷2.4
x=75
答:乙车的速度是75千米/时。
https://www.21cnjy.com/recruitment/home/fine
专题三:数与方程
思维导图
01
用字母表示数
知识清单
1、用字母表示常见的数量关系
①路程(s)、速度(v)、时间(t)三者之间的关系:s=vt
②总价(a)、单价(b)、数量(c)三者之间的关系:a=bc b=a÷c c=a÷b
2、用字母表示运算律和运算性质
(1)运算律
加法交换律:a+b=b+a 加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:a×(b+c)=a×b+a×c
(2)运算性质
减法性质:a-(b+c)=a-b-c a+(b-c)=a+b-c a-(b-c)=a-b+c
除法性质:a÷(b×c)=a÷b÷c
01
用字母表示数
知识清单
3、用字母表示计算公式
(1)周长
长方形:C=2(a+b)
正方形:C=4a
圆:C=2πr=πd
(3)表面积
长方体:S=2(ab+ah+bh)
正方体:S=6a
圆柱:S=2πrh+2πr
(2)面积
长方形:S=ab
正方形:S=a
平行四边形:S=ah
三角形:S=ah÷2
梯形:S=(a+b)h÷2
圆:S=πr
(4)体积
长方体:V=abh
正方体:V=a
圆柱:V=Sh
圆锥:
02
解方程
知识清单
1、方程的意义:根据等量关系列出的含有未知数的等式叫作方程。
2、等式的性质
①等式两边同时加上或减去相同的数,所得结果仍然是等式
②等式两边同时乘或除以一个相同的数(0除外),所得结果仍然是等式
02
解方程
知识清单
3、解方程
①方程的解:使方程左右两边相等的未知数的值叫作方程的解。
举例:x=3是方程8x=24的解
②解方程:求方程中未知数的值的过程叫作解方程。
03
列方程解决问题
知识清单
1.列方程解应用题步骤
①根据题意,确定未知数,并用x (或其他字母)表示
②找数量间的相等关系(画图、根据公式、根据关键句、根据常见的数量关系)
③列方程
④解方程
⑤检验并写出答案
04
题型训练
例题精讲
01 用字母表示数
1.用小棒摆五边形,如图:按这个规律,摆n个五边形,需要( )根小棒;照这样摆,用97根小棒能摆( )个五边形。
【答案】4n+1 24
【解答】5+4×(n-1)
=5+4n-4
=(4n+1)根
(97-1)÷4
=96÷4
=24(个)
用小棒摆五边形,如图:按这个规律,摆n个五边形,需要(4n+1)根小棒;照这样摆,用97根小棒能摆24个五边形。
04
题型训练
例题精讲
01 用字母表示数
2.每张课桌的价钱是m元,椅子比课桌便宜30元,那么m-30表示的是( ),m+(m―30)表示( ),如果2张桌子和4把椅子的价格相等,将这一关系用含有字母的等式表示出来是( )。
【答案】一把椅子的价钱 一把椅子和一张桌子的总价钱 2m=4(m-30)
【解答】每张椅子比课桌便宜30元,即每张椅子=每张课桌的价钱-30=m-30。
m+(m―30),其中m表示每张课桌的价钱,(m-30)表示每张椅子的价钱,因此m+(m―30)表示一张椅子和一张桌子的总价钱。
2张桌子的价钱表示为2m,4把椅子的价钱表示为4(m-30),2张桌子和4把椅子的价格相等,即2m=4(m-30)。
因此m-30表示的是一张椅子的价钱;m+(m―30)表示一张椅子和一张桌子的总价钱;如果2张桌子和4把椅子的价格相等,将这一关系用含有字母的等式表示出来是2m=4(m-30)。
04
题型训练
例题精讲
02 解方程
1.解方程。
【答案】x=15;x=3
【解答】(1)x÷1.5=10
解:x÷1.5×1.5=10×1.5
x=15
(2)0.4x+0.6×2.5=2.7
解:0.4x+1.5=2.7
0.4x+1.5-1.5=2.7-1.5
0.4x=1.2
0.4x÷0.4=1.2÷0.4
x=3
04
题型训练
例题精讲
02 解方程
2.在天平的“?”处添加下列物品后,天平不能保持平衡的是( )。
A. B. C. D.
【答案】A
【解答】A.天平右端原有2个正方体,再添加 6个正方体,则右端有2+6=8个正方体,天平不能保持平衡;
B.天平右端原有2个正方体,再添加 ,相当于添加2+2=4个正方体,则右端有2+4=6个正方体,天平能保持平衡;
C.天平右端原有2个正方体,再添加 ,相当于添加2+2=4个正方体,则右端有2+4=6个正方体,天平能保持平衡;
D.天平右端原有2个正方体,再添加 4个正方体,则右端有2+4=6个正方体,天平能保持平衡。 故答案为:A
04
题型训练
例题精讲
03 列方程解决问题
1.一队少先队员乘船过河,如果每船坐15人,还剩9人;如果每船坐18人,刚好剩余1只船。共有多少只船?(用方程解答)
【答案】9只
【解答】解:设共有x只船。
15x+9=(x-1)×18
15x+9=18x-18
15x+9-15x=18x-18-15x
9=3x-18
3x-18+18=9+18
3x=27
3x÷3=27÷3
x=9 答:共有9只船。
04
题型训练
例题精讲
03 列方程解决问题
2.如图,大长方形由9个正方形组成,已知中间最小的正方形边长为1厘米,求大长方形的周长。
【答案】C
【解答】解:设右上角的正方形边长为x厘米,则9个正方形的边长从小到大依次是1、x、2x、2x+1、2x+2、2x+3。
x+x+2x+2x+1=2x+3+2x+2
6x+1=4x+5
6x-4x=5-1
2x=4
x=4÷2
x=2
长:2×2+1+2×2+2+2
=13(厘米)
2×2+1+2×2+2
=11(厘米)
(13+11)×2
=24×2
=48(厘米)
答:大长方形的周长是48厘米。
05
专项训练
专项练习
1.食堂买来a袋大米,每袋25千克,已经吃了b千克,还剩( )千克;当a=20,b=375时,则还剩( )千克。
2.一张长方形的纸,剪去一个长acm、宽3cm的长方形以后就变成了一个正方形(如图),则原来长方形的周长是( )cm,面积是( )cm2。
25a-b
a2+3a
4a+6
125
05
专项训练
专项练习
3.a是一个不为0的数,当a=( )时,a2=2a;当a<2时,a2( )2a。
4.下面这些式子中,等式有( ),方程有( )。(填序号)
①x-30=26 ②25×2=50 ③6+m ④ 5a<2.5 ⑤ x÷0.3=1.2
2
①②⑤
①⑤
<
05
专项训练
专项练习
5.根据题意写出等量关系式,再列方程。
冬冬看一本360页的书,他每天看x页,看了5天后还剩45页没有看。
(1)( )-( )=( )
方程: 。
(2)( )+( )=( )
方程: 。
6.一个两位数,十位上的数字是a,个位上的数字是b,这个两位数用含有字母的式子表示是( )。
A.ab B.10a+b C.10b+a D.10(a+b)
书的总页数
已经看的页数
剩下没看的页数
360-5x=45
已经看的页数
剩下没看的页数
书的总页数
5x+45=360或45+5x=360
B
05
专项训练
专项练习
7.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出4千克放入乙袋,那么甲、乙两袋质量相等。列成等式是( )。
A.a+4=b-4 B.a-b=4 C.(a+b)÷2=4 D.a-4=b+4
8.六年级两个班上交的绘画作品情况如图所示,下列等量关系错误的是( )。
A. x B. C.
B
D
05
专项训练
专项练习
9.下列选项中,不能用方程“x+3x=44”来解释的是( )。
A.
B.
C.一个长方形周长是44dm。长为3x dm,宽为x dm。
D.全班有44人,其中男生有x人,女生是男生的3倍。
10.一个足球的表面由一些黑色五边形和白色六边形组成,如下图所示,每个五边形周围有5个六边形,每个六边形周围有3个五边形。已知五边形的总数是12,那么六边形的总数是( )。
A.20 B.30 C.40 D.50
C
A
05
专项训练
专项练习
11.爸爸、哥哥、妹妹三人现在的年龄和是64岁,当爸爸的年龄是哥哥年龄的3倍时,妹妹是9岁。当哥哥的年龄是妹妹年龄的2倍时,爸爸是34岁。现在哥哥的年龄是几岁?
解:设哥哥年龄是x岁,那么爸爸是3x岁。
3x-x=34-2×(x-9)
2x=34-2x+18
4x=52
x=52÷4
x=13
哥哥与妹妹年龄差为:13-9=4(岁)
此时爸爸年龄为:13×3=39(岁)
爸爸与哥哥的年龄差为:39-13=26(岁)
64-26+4
=38+4
=42(岁)
现在哥哥年龄:42÷3=14(岁)
答:现在哥哥14岁。
05
专项训练
专项练习
12.蟋蟀的鸣叫是大自然的音乐,并且蟋蟀鸣叫的频率与气温有着很大的关系。人们发现某地某种蟋蟀每分钟鸣叫的次数和气温之间有以下的关系:用蟋蟀1分钟鸣叫的次数除以7,再加上3,结果等于该地当时的气温(单位℃)。
(1)如果用T表示该地当时的气温,m表示蟋蟀每分钟鸣叫的次数,请用含有字母的式子表示T和m的关系。
(2)当m=203时,该地当时的气温是多少摄氏度?
(1)T=m÷7+3
答:用含有字母的式子表示T和m的关系为:T=m÷7+3。
(2)203÷7+3
=29+3
=32(摄氏度)
答:该地当时的气温是32摄氏度。
05
专项训练
专项练习
13.某市出租车收费标准如下:3千米以内(含3千米)收8元,超过3千米的部分,每千米收2.4元。张叔叔坐出租车从体育馆到火车站一共行了b(b>3)千米。
(1)用含有字母的式子,表示张叔叔坐出租车从体育馆到火车站,一共花了多少钱?
(2)当b=10时,张叔叔坐出租车从体育馆到火车站一共花了多少钱?
(1)行驶3千米的费用:8元;
超过3千米部分的费用:[2.4×(b-3)]元;
一共:8+2.4×(b-3)
=8+2.4×b-2.4×3
=(2.4b+0.8)元
答:张叔叔坐出租车从体育馆到火车站,一共花(2.4b+0.8)元。
(2)当b=10时
2.4b+0.8
=10×2.4+0.8
=24+0.8
=24.8(元)
答:当b=10时,张叔叔坐出租车从体育馆到火车站一共花了24.8元。
05
专项训练
专项练习
14.供水公司为了鼓励居民节约用水,规定:每户每月用水不超过5立方米时,按每立方米1.6元收费;超过5立方米的部分按每立方米4元收费。王丽家5月份平均每立方米水费是2.5元,请你算一算,王丽家5月份共交水费多少元?
解:设王丽家5月份用水x立方米。
5×1.6+(x-5)×4=2.5x
8+4x-20=2.5x
8+4x-20+20-8=2.5x+20-8
4x =2.5x+12
4x-2.5x =2.5x+12-2.5x
1.5x=12
1.5x÷1.5=12÷1.5
x=8
2.5×8=20(元)
答:王丽家5月份共交水费20元。
05
专项训练
专项练习
15.甲乙两车从相距360千米的A,B两地同时出发相向而行,甲车的速度是乙车的1.4倍,2小时后相遇。求乙车的速度?
解:设乙车的速度是x千米/时,则甲车的速度是1.4x千米/时。
(x+1.4x)×2=360
2.4x×2=360
2.4x×2÷2=360÷2
2.4x=180
2.4x÷2.4=180÷2.4
x=75
答:乙车的速度是75千米/时。
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
