人教(2019A版)高一下期中测试卷1-3章(含解析)
文档属性
| 名称 | 人教(2019A版)高一下期中测试卷1-3章(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 438.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 09:24:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高一下期中测试卷1-3章(含解析)
一、单选题
1.设复数z满足 ,其中i为虚数单位,则z=( )
A. B. C. D.
2.已知平面向量,,则向量在向量上的投影向量是( )
A. B. C. D.
3.设m,n是空间两条不同直线, , 是空间两个不同平面,则下列选项中不正确的是( )
A.当n⊥ 时,“n⊥ ”是“ ∥ ”成立的充要条件
B.当 时,“m⊥ ”是“ ”的充分不必要条件
C.当 时,“n// ”是“ ”必要不充分条件
D.当 时,“n⊥ ”是“ ”的充分不必要条件
4.若底面半径为r,母线长为l的圆锥的表面积与直径也为l的球的表面积相等,则( )
A. B. C. D.
5.在中,角A,B,C的对边分别为a,b,c,向量与平行.若,,则BC边上的中线AD为( )
A.1 B.2 C. D.
6.已知平行四边形 中, , ,对角线 与 相交于点 ,点 是线段 上一点,则 的最小值为( )
A. B. C. D.
7.圣·索菲亚教堂坐落于中国黑龙江省,是每一位到哈尔滨旅游的游客拍照打卡的必到景点.其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点(,,三点共线)处测得楼顶,教堂顶的仰角分别是15°和60°,在楼顶处测得塔顶的仰角为30°,则小明估算索菲亚教堂的高度为( )
A. B. C. D.
8.在棱长为的正方体中,,,分别为棱,,的中点,动点在平面内,且.则下列说法正确的是( )
A.存在点,使得直线与直线相交
B.存在点,使得直线平面
C.直线与平面所成角的大小为
D.平面被正方体所截得的截面面积为
二、多选题
9.设复数z在复平面内对应的点为Z,原点为O,i为虚数单位,则下列说法正确的是( )
A.若|z|=1,则z=±1或z=±i
B.若点Z的坐标为(-1,l),则z+1是纯虚数
C.若 ,则z的虚部为-2i
D.若 ,则点Z的集合所构成的图形的面积为
10.下列关于空间向量的命题中,正确的有( )
A.若向量 , 与空间任意向量都不能构成基底,则 ;
B.若非零向量 , , 满足 , ,则有 ;
C.若 , , 是空间的一组基底,且 ,则 , , , 四点共面;
D.若向量 , , ,是空间一组基底,则 , , 也是空间的一组基底.
11.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马,将四个面均为直角三角形的四面体称为鳖臑.如图在堑堵中,,,,分别为棱,的中点,则( )
A.四面体为鳖臑 B.平面
C.若,则与所成角的正切值为 D.三棱锥的外接球的体积为定值
三、填空题
12.平面向量 满足 , , ,则 .
13.已知在边长为2的正三角形 中, 、 分别为边 、 上的动点,且 ,则 的最大值为 .
14.地球仪是地理教学中的常用教具.如图1所示,地球仪的赤道面(与转轴垂直)与黄道面(与水平面平行)存在一个夹角,即黄赤交角,大小约为23.5°.为锻炼动手能力,某同学制作了一个半径为4cm的地球仪(不含支架),并将其放入竖直放置的正三棱柱中(姿态保持不变),使地球仪与该三棱柱的三个侧面相切,如图2所示.此时平面恰与地球仪的赤道面平行,则三棱柱的外接球体积为 .(参考数据:)
四、解答题
15.已知向量,.
(1)若,求及在上投影的数量;
(2)若,求与的夹角.
16.在①,②,③这三个条件中任选一个,补充在下面的问题中并解答.
问题:在中,内角的对边分别为,且满足____.
(1)求角;
(2)若,求的面积.
注:如果选择多个条件分别解答,按第一个解答计分.
17.如图,在直角梯形AEFB中, , ,且 ,直角梯形 可以通过直角梯形AEFB以直线EF为轴旋转得到.
(1)求证:平面 平面 ;
(2)若二面角 的大小为 ,求直线 与平面 所成角的正弦值.
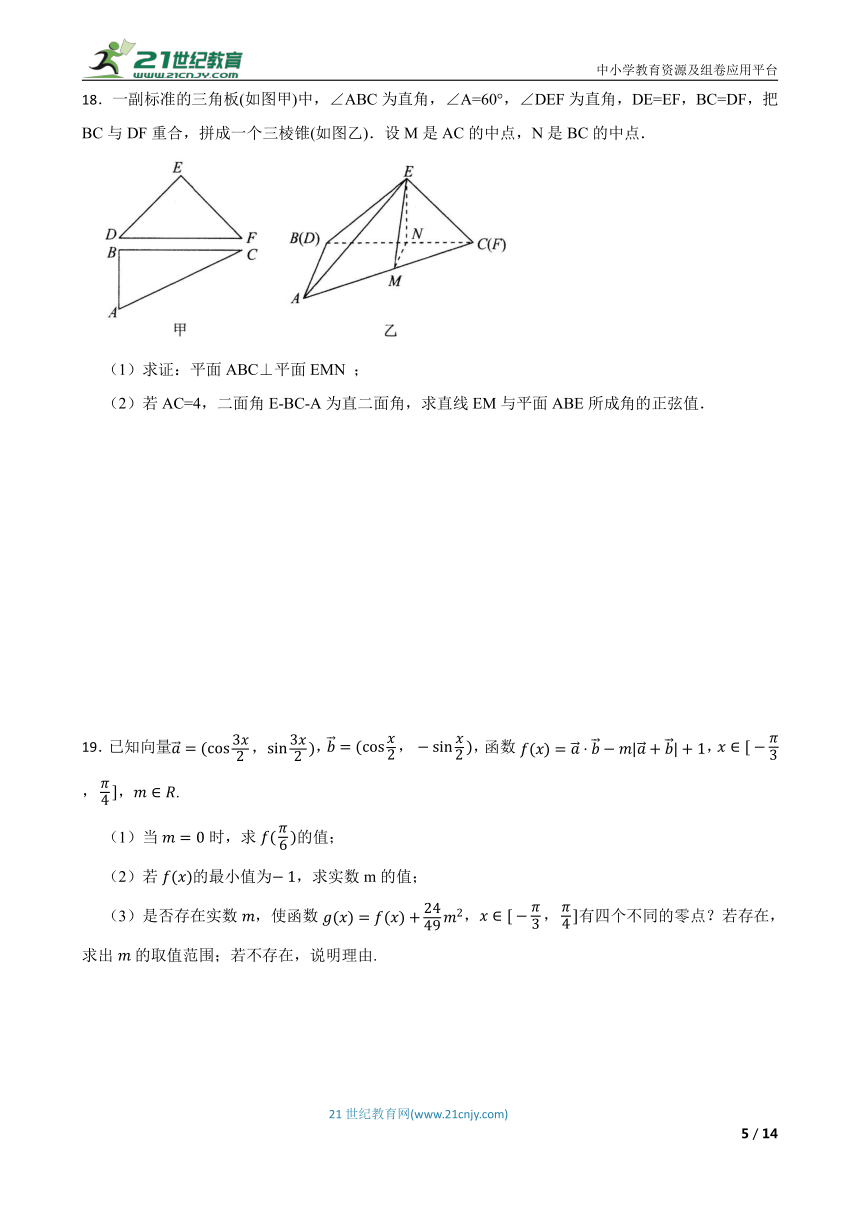
18.一副标准的三角板(如图甲)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF,把BC与DF重合,拼成一个三棱锥(如图乙).设M是AC的中点,N是BC的中点.
(1)求证:平面ABC⊥平面EMN ;
(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成角的正弦值.
19.已知向量,,函数,,.
(1)当时,求的值;
(2)若的最小值为,求实数m的值;
(3)是否存在实数,使函数,有四个不同的零点?若存在,求出的取值范围;若不存在,说明理由.
答案解析部分
1.【答案】B
【解析】【解答】因为复数z满足 ,
所以 .
故答案为:B.
【分析】根据题意由复数的运算性质化简复数z即可。
2.【答案】B
3.【答案】C
【解析】【解答】A,B,D符合题意,C不符合题意。 异面;
所以当 时, 是 的既不充分又不必要条件,故答案为:C。
【分析】利用已知条件结合充分条件、必要条件的判断方法,从而推出当 时,“n// ”是“ ”必要不充分条件。
4.【答案】D
【解析】【解答】解:圆锥的表面积为,球的表面积为,
故,即,故(负舍).
故答案为:D.
【分析】先利用圆锥表面积公式和球的表面公式可列出方程,解方程可求出的值.
5.【答案】D
6.【答案】A
【解析】【解答】解:如图,以BD的中点为原点,分别以BD,CA所在直线为x,y轴建立平面直接坐标系,
则B(-1,0),,
所以直线BC的方程为:,
设点M,
所以
所以
故当时,取得最小值为
故答案为:A
【分析】根据向量的数量积的坐标表示,结合二次函数的最值问题直接求解即可.
7.【答案】D
【解析】【解答】解:在直角三角形中,.
在中,,,
故,
由正弦定理,,
故.
在直角三角形中,.
故答案为:D.
【分析】 由正弦得出AM,再结合正弦定理得到CM,进而能求出CD.
8.【答案】C
9.【答案】B,D
【解析】【解答】解:对于A,若,则|z|=1,所以A错误,
对于B,由于点Z的坐标为(-1, I) ,所以z= -1+i,所以z+ 1= i是纯虚数,所以B正确,
对于C,由于,所以的虚部为- 2,所以C错误,
对于D,设z=a+bi,则,因为1≤lz|≤2,所以,所以点Z的集合所构成的图形的面积为,所以D正确.
故答案为:BD
【分析】对于A,举例判断即可,对于B,直接求解即可,对于C,由已知直接判断,对于D,根据复数的几何意义求解即可.
10.【答案】A,C,D
【解析】【解答】解:对于A:若向量 , 与空间任意向量都不能构成基底,只能两个向量为共线向量,即 ,A符合题意;
对于B:若非零向量 , , 满足 , ,则 与 不一定共线,B不符合题意;
对于C:若 , , 是空间的一组基底,且 ,
则 ,即 ,
可得到 , , , 四点共面,C符合题意;
对于D:若向量 , , ,是空间一组基底,
则空间任意一个向量 ,存在唯一实数组 ,
使 ,
则 , , 也是空间的一组基底.
故答案为:ACD.
【分析】根据空间向量基本定理,能作为基底的向量一定是不共面的向量,由此分别分析选项,即可得到答案。
11.【答案】A,B,D
【解析】【解答】解:对于 ,在三棱柱 中,
平面 , ,
又 ,且 ,
平面 ,且 平面 ,
,
又 平面 , , ,
即四面体 为鳖臑,故 正确;
对于 ,连接 和 中点 ,交 于 ,
则 为 的中点,易得 ,即四边形 为平行四边形,
所以 ,且 平面 , 平面 ,
易知 平面 ,故 正确;
对于 ,由 可知 为 与 所成角,
在 中, , ,则 ,
可知 与 所成角的正切值为 ,故 错误,
对于 ,可知三棱锥 的外接球的半径为 ,所以体积为 ,故 正确.
故答案为:ABD
【分析】利用已知条件结合鳖臑的定义、 线面平行的判定定理、正切函数的定义、三棱锥与外接球的位置关系、球的体积公式,进而找出正确的选项。
12.【答案】
【解析】【解答】 , ,
,解得: ,
, 。
故答案为: 。
【分析】利用已知条件结合数量积的运算法则和数量积的定义,再结合向量的模的坐标表示,从而求出的值,再利用数量积求向量的模的公式结合数量积的定义,从而求出的值。
13.【答案】
【解析】【解答】解:如图,建立恰当的直角坐标系,
则B(-1,0),C(1,0),A,
则
设 (0≤t≤l),则 (0≤t≤1),
则,
则,
则,
当t=时,取得最大值.
故答案为:.
【分析】如图建立直角坐标系,设 (0≤t≤l),则 (0≤t≤1),然后表示出 可求得其最大值.
14.【答案】
15.【答案】(1),
(2)
16.【答案】(1)解:若选①,,即,
由正弦定理得,
因为,所以,
所以,化简得,
所以,因为,所以,所以.
若选②因为,由正弦定理可得,
整理得,
又,
所以.
又因为,可得,所以,
又,所以.
若选③,由,
得,
由正弦定理得,整理得,
所以,又,所以.
(2)解:因为,由余弦定理得,
又,所以,即,解得,
则的面积.
【解析】【分析】(1) 若选① ,首先由正弦定理整理化简已知条件结合两角和的余弦公式,代入数值计算出coaA的取值,从而得出角A的大小。 若选② ,由正弦定理整理化简原式然后由两角和的余弦公式,计算出cosA的取值,由此得出角A的取值。 若选③ 首先整理化简原式再由正弦定理,计算出a、b、c之间的关系,并代入到余弦定理由此计算出cosA的取值,从而得出角A的大小。
(2)由(1)的结论结合余弦定理代入数值计算出bc的取值,并代入到三角形面积公式由此计算出结果。
17.【答案】(1)证明:在直角梯形AEFB中, ,且直角梯形 是通过直角梯形AEFB以直线EF为轴旋转而得,
所以 ,所以 , .
所以 平面 .
所以平面 平面
(2)解:由(1)可知 , .
因为二面角 为 ,所以
过点F作平面AEFB的垂线,如图,建立空间直角坐标系 .
设 ,则: , , , , .
所以 , , , .
设平面 的法向量为 ,则 即
令 ,则 , .
于是 .
所以直线 与平面 所成角的正弦值
【解析】【分析】(1)根据平面与平面垂直的判定定理即可求证;
(2)根据向量法,结合二面角的解法,运用向量法即可求解直线与平面所成角.
18.【答案】(1)∵M是AC的中点,N是BC的中点,∴MN P AB
∵AB⊥BC,∴MN⊥BC,∵BE⊥EC,BE=EC,N是BC的中点,
∴EN⊥BC,
又MN∩EN=N,MN 平面EMN,EN 平面EMN
∴BC⊥平面EMN且BC 平面 ABC
∴平面ABC⊥平面EMN
(2)由(1)可知:EN⊥BC,MN⊥BC,
∴∠ENM为二面角E-BC-A的平面角
又二面角E-BC-A为直二面角.
∠ENM = 90°
以NM,NC,NE分别为x,y,z,建立如图空间直角坐标系N-xyz.
∵AC=4,则AB=2,BC=2 ,NE=
由E(0,0, ),M(1,0,0),
则 =(,0,- )
B(0,- ,0),A(2,- ,0),E(0,0, ),
则 =(0, , ), =(2,0,0)
设 =(x,y,z)为平面ABE的一个法向量,则
即
令y=1,则z=-1,面4BE的一个法向量 =(0,1,-1)
|cos< , >|=
所以直线EM与平面ABE所成的角的正弦值为
【解析】【分析】(1)根据直线与平面垂直的判定定理,以及平面与平面垂直的判定定理求解即可;
(2)利用向量法直接求解即可.
19.【答案】(1)解:,
当时,,
则;
(2)解:∵,
∴,
则,
令,则,
则,对称轴,
① 当,即时,
当时,函数取得最小值,此时最小值,得(舍),
② 当,即时,
当时,函数取得最小值,此时最小值,得,
③ 当,即时,
当时,函数取得最小值,此时最小值,得(舍),
综上若的最小值为,则实数;
(3)解:令,得或,
∴方程或在上有四个不同的实根,
则,得,则,
即实数m的取值范围是.
【解析】【分析】(1)利用已知条件结合数量积的坐标表示和m的值结合两角和的余弦公式,进而得出函数的解析式,再结合代入法得出函数的值。
(2)利用已知条件结合x的取值范围和数量积求向量的模的公式和同角三角函数基本关系式和二倍角的余弦公式,再利用换元法得出函数为二次函数,再结合二次函数的图象和定义域以及对称性,进而得出二次函数的最小值,进而得出实数m的值。
(3)利用函数的零点求解方法结合函数的零点与方程的根的等价关系,再利用已知条件,进而得出实数m的取值范围。
21世纪教育网(www.21cnjy.com)
1 / 1
高一下期中测试卷1-3章(含解析)
一、单选题
1.设复数z满足 ,其中i为虚数单位,则z=( )
A. B. C. D.
2.已知平面向量,,则向量在向量上的投影向量是( )
A. B. C. D.
3.设m,n是空间两条不同直线, , 是空间两个不同平面,则下列选项中不正确的是( )
A.当n⊥ 时,“n⊥ ”是“ ∥ ”成立的充要条件
B.当 时,“m⊥ ”是“ ”的充分不必要条件
C.当 时,“n// ”是“ ”必要不充分条件
D.当 时,“n⊥ ”是“ ”的充分不必要条件
4.若底面半径为r,母线长为l的圆锥的表面积与直径也为l的球的表面积相等,则( )
A. B. C. D.
5.在中,角A,B,C的对边分别为a,b,c,向量与平行.若,,则BC边上的中线AD为( )
A.1 B.2 C. D.
6.已知平行四边形 中, , ,对角线 与 相交于点 ,点 是线段 上一点,则 的最小值为( )
A. B. C. D.
7.圣·索菲亚教堂坐落于中国黑龙江省,是每一位到哈尔滨旅游的游客拍照打卡的必到景点.其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点(,,三点共线)处测得楼顶,教堂顶的仰角分别是15°和60°,在楼顶处测得塔顶的仰角为30°,则小明估算索菲亚教堂的高度为( )
A. B. C. D.
8.在棱长为的正方体中,,,分别为棱,,的中点,动点在平面内,且.则下列说法正确的是( )
A.存在点,使得直线与直线相交
B.存在点,使得直线平面
C.直线与平面所成角的大小为
D.平面被正方体所截得的截面面积为
二、多选题
9.设复数z在复平面内对应的点为Z,原点为O,i为虚数单位,则下列说法正确的是( )
A.若|z|=1,则z=±1或z=±i
B.若点Z的坐标为(-1,l),则z+1是纯虚数
C.若 ,则z的虚部为-2i
D.若 ,则点Z的集合所构成的图形的面积为
10.下列关于空间向量的命题中,正确的有( )
A.若向量 , 与空间任意向量都不能构成基底,则 ;
B.若非零向量 , , 满足 , ,则有 ;
C.若 , , 是空间的一组基底,且 ,则 , , , 四点共面;
D.若向量 , , ,是空间一组基底,则 , , 也是空间的一组基底.
11.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马,将四个面均为直角三角形的四面体称为鳖臑.如图在堑堵中,,,,分别为棱,的中点,则( )
A.四面体为鳖臑 B.平面
C.若,则与所成角的正切值为 D.三棱锥的外接球的体积为定值
三、填空题
12.平面向量 满足 , , ,则 .
13.已知在边长为2的正三角形 中, 、 分别为边 、 上的动点,且 ,则 的最大值为 .
14.地球仪是地理教学中的常用教具.如图1所示,地球仪的赤道面(与转轴垂直)与黄道面(与水平面平行)存在一个夹角,即黄赤交角,大小约为23.5°.为锻炼动手能力,某同学制作了一个半径为4cm的地球仪(不含支架),并将其放入竖直放置的正三棱柱中(姿态保持不变),使地球仪与该三棱柱的三个侧面相切,如图2所示.此时平面恰与地球仪的赤道面平行,则三棱柱的外接球体积为 .(参考数据:)
四、解答题
15.已知向量,.
(1)若,求及在上投影的数量;
(2)若,求与的夹角.
16.在①,②,③这三个条件中任选一个,补充在下面的问题中并解答.
问题:在中,内角的对边分别为,且满足____.
(1)求角;
(2)若,求的面积.
注:如果选择多个条件分别解答,按第一个解答计分.
17.如图,在直角梯形AEFB中, , ,且 ,直角梯形 可以通过直角梯形AEFB以直线EF为轴旋转得到.
(1)求证:平面 平面 ;
(2)若二面角 的大小为 ,求直线 与平面 所成角的正弦值.
18.一副标准的三角板(如图甲)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF,把BC与DF重合,拼成一个三棱锥(如图乙).设M是AC的中点,N是BC的中点.
(1)求证:平面ABC⊥平面EMN ;
(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成角的正弦值.
19.已知向量,,函数,,.
(1)当时,求的值;
(2)若的最小值为,求实数m的值;
(3)是否存在实数,使函数,有四个不同的零点?若存在,求出的取值范围;若不存在,说明理由.
答案解析部分
1.【答案】B
【解析】【解答】因为复数z满足 ,
所以 .
故答案为:B.
【分析】根据题意由复数的运算性质化简复数z即可。
2.【答案】B
3.【答案】C
【解析】【解答】A,B,D符合题意,C不符合题意。 异面;
所以当 时, 是 的既不充分又不必要条件,故答案为:C。
【分析】利用已知条件结合充分条件、必要条件的判断方法,从而推出当 时,“n// ”是“ ”必要不充分条件。
4.【答案】D
【解析】【解答】解:圆锥的表面积为,球的表面积为,
故,即,故(负舍).
故答案为:D.
【分析】先利用圆锥表面积公式和球的表面公式可列出方程,解方程可求出的值.
5.【答案】D
6.【答案】A
【解析】【解答】解:如图,以BD的中点为原点,分别以BD,CA所在直线为x,y轴建立平面直接坐标系,
则B(-1,0),,
所以直线BC的方程为:,
设点M,
所以
所以
故当时,取得最小值为
故答案为:A
【分析】根据向量的数量积的坐标表示,结合二次函数的最值问题直接求解即可.
7.【答案】D
【解析】【解答】解:在直角三角形中,.
在中,,,
故,
由正弦定理,,
故.
在直角三角形中,.
故答案为:D.
【分析】 由正弦得出AM,再结合正弦定理得到CM,进而能求出CD.
8.【答案】C
9.【答案】B,D
【解析】【解答】解:对于A,若,则|z|=1,所以A错误,
对于B,由于点Z的坐标为(-1, I) ,所以z= -1+i,所以z+ 1= i是纯虚数,所以B正确,
对于C,由于,所以的虚部为- 2,所以C错误,
对于D,设z=a+bi,则,因为1≤lz|≤2,所以,所以点Z的集合所构成的图形的面积为,所以D正确.
故答案为:BD
【分析】对于A,举例判断即可,对于B,直接求解即可,对于C,由已知直接判断,对于D,根据复数的几何意义求解即可.
10.【答案】A,C,D
【解析】【解答】解:对于A:若向量 , 与空间任意向量都不能构成基底,只能两个向量为共线向量,即 ,A符合题意;
对于B:若非零向量 , , 满足 , ,则 与 不一定共线,B不符合题意;
对于C:若 , , 是空间的一组基底,且 ,
则 ,即 ,
可得到 , , , 四点共面,C符合题意;
对于D:若向量 , , ,是空间一组基底,
则空间任意一个向量 ,存在唯一实数组 ,
使 ,
则 , , 也是空间的一组基底.
故答案为:ACD.
【分析】根据空间向量基本定理,能作为基底的向量一定是不共面的向量,由此分别分析选项,即可得到答案。
11.【答案】A,B,D
【解析】【解答】解:对于 ,在三棱柱 中,
平面 , ,
又 ,且 ,
平面 ,且 平面 ,
,
又 平面 , , ,
即四面体 为鳖臑,故 正确;
对于 ,连接 和 中点 ,交 于 ,
则 为 的中点,易得 ,即四边形 为平行四边形,
所以 ,且 平面 , 平面 ,
易知 平面 ,故 正确;
对于 ,由 可知 为 与 所成角,
在 中, , ,则 ,
可知 与 所成角的正切值为 ,故 错误,
对于 ,可知三棱锥 的外接球的半径为 ,所以体积为 ,故 正确.
故答案为:ABD
【分析】利用已知条件结合鳖臑的定义、 线面平行的判定定理、正切函数的定义、三棱锥与外接球的位置关系、球的体积公式,进而找出正确的选项。
12.【答案】
【解析】【解答】 , ,
,解得: ,
, 。
故答案为: 。
【分析】利用已知条件结合数量积的运算法则和数量积的定义,再结合向量的模的坐标表示,从而求出的值,再利用数量积求向量的模的公式结合数量积的定义,从而求出的值。
13.【答案】
【解析】【解答】解:如图,建立恰当的直角坐标系,
则B(-1,0),C(1,0),A,
则
设 (0≤t≤l),则 (0≤t≤1),
则,
则,
则,
当t=时,取得最大值.
故答案为:.
【分析】如图建立直角坐标系,设 (0≤t≤l),则 (0≤t≤1),然后表示出 可求得其最大值.
14.【答案】
15.【答案】(1),
(2)
16.【答案】(1)解:若选①,,即,
由正弦定理得,
因为,所以,
所以,化简得,
所以,因为,所以,所以.
若选②因为,由正弦定理可得,
整理得,
又,
所以.
又因为,可得,所以,
又,所以.
若选③,由,
得,
由正弦定理得,整理得,
所以,又,所以.
(2)解:因为,由余弦定理得,
又,所以,即,解得,
则的面积.
【解析】【分析】(1) 若选① ,首先由正弦定理整理化简已知条件结合两角和的余弦公式,代入数值计算出coaA的取值,从而得出角A的大小。 若选② ,由正弦定理整理化简原式然后由两角和的余弦公式,计算出cosA的取值,由此得出角A的取值。 若选③ 首先整理化简原式再由正弦定理,计算出a、b、c之间的关系,并代入到余弦定理由此计算出cosA的取值,从而得出角A的大小。
(2)由(1)的结论结合余弦定理代入数值计算出bc的取值,并代入到三角形面积公式由此计算出结果。
17.【答案】(1)证明:在直角梯形AEFB中, ,且直角梯形 是通过直角梯形AEFB以直线EF为轴旋转而得,
所以 ,所以 , .
所以 平面 .
所以平面 平面
(2)解:由(1)可知 , .
因为二面角 为 ,所以
过点F作平面AEFB的垂线,如图,建立空间直角坐标系 .
设 ,则: , , , , .
所以 , , , .
设平面 的法向量为 ,则 即
令 ,则 , .
于是 .
所以直线 与平面 所成角的正弦值
【解析】【分析】(1)根据平面与平面垂直的判定定理即可求证;
(2)根据向量法,结合二面角的解法,运用向量法即可求解直线与平面所成角.
18.【答案】(1)∵M是AC的中点,N是BC的中点,∴MN P AB
∵AB⊥BC,∴MN⊥BC,∵BE⊥EC,BE=EC,N是BC的中点,
∴EN⊥BC,
又MN∩EN=N,MN 平面EMN,EN 平面EMN
∴BC⊥平面EMN且BC 平面 ABC
∴平面ABC⊥平面EMN
(2)由(1)可知:EN⊥BC,MN⊥BC,
∴∠ENM为二面角E-BC-A的平面角
又二面角E-BC-A为直二面角.
∠ENM = 90°
以NM,NC,NE分别为x,y,z,建立如图空间直角坐标系N-xyz.
∵AC=4,则AB=2,BC=2 ,NE=
由E(0,0, ),M(1,0,0),
则 =(,0,- )
B(0,- ,0),A(2,- ,0),E(0,0, ),
则 =(0, , ), =(2,0,0)
设 =(x,y,z)为平面ABE的一个法向量,则
即
令y=1,则z=-1,面4BE的一个法向量 =(0,1,-1)
|cos< , >|=
所以直线EM与平面ABE所成的角的正弦值为
【解析】【分析】(1)根据直线与平面垂直的判定定理,以及平面与平面垂直的判定定理求解即可;
(2)利用向量法直接求解即可.
19.【答案】(1)解:,
当时,,
则;
(2)解:∵,
∴,
则,
令,则,
则,对称轴,
① 当,即时,
当时,函数取得最小值,此时最小值,得(舍),
② 当,即时,
当时,函数取得最小值,此时最小值,得,
③ 当,即时,
当时,函数取得最小值,此时最小值,得(舍),
综上若的最小值为,则实数;
(3)解:令,得或,
∴方程或在上有四个不同的实根,
则,得,则,
即实数m的取值范围是.
【解析】【分析】(1)利用已知条件结合数量积的坐标表示和m的值结合两角和的余弦公式,进而得出函数的解析式,再结合代入法得出函数的值。
(2)利用已知条件结合x的取值范围和数量积求向量的模的公式和同角三角函数基本关系式和二倍角的余弦公式,再利用换元法得出函数为二次函数,再结合二次函数的图象和定义域以及对称性,进而得出二次函数的最小值,进而得出实数m的值。
(3)利用函数的零点求解方法结合函数的零点与方程的根的等价关系,再利用已知条件,进而得出实数m的取值范围。
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
