【核心考点集训】第四单元《比例》学案--人教版六年级下册数学
文档属性
| 名称 | 【核心考点集训】第四单元《比例》学案--人教版六年级下册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 12:05:18 | ||
图片预览




文档简介
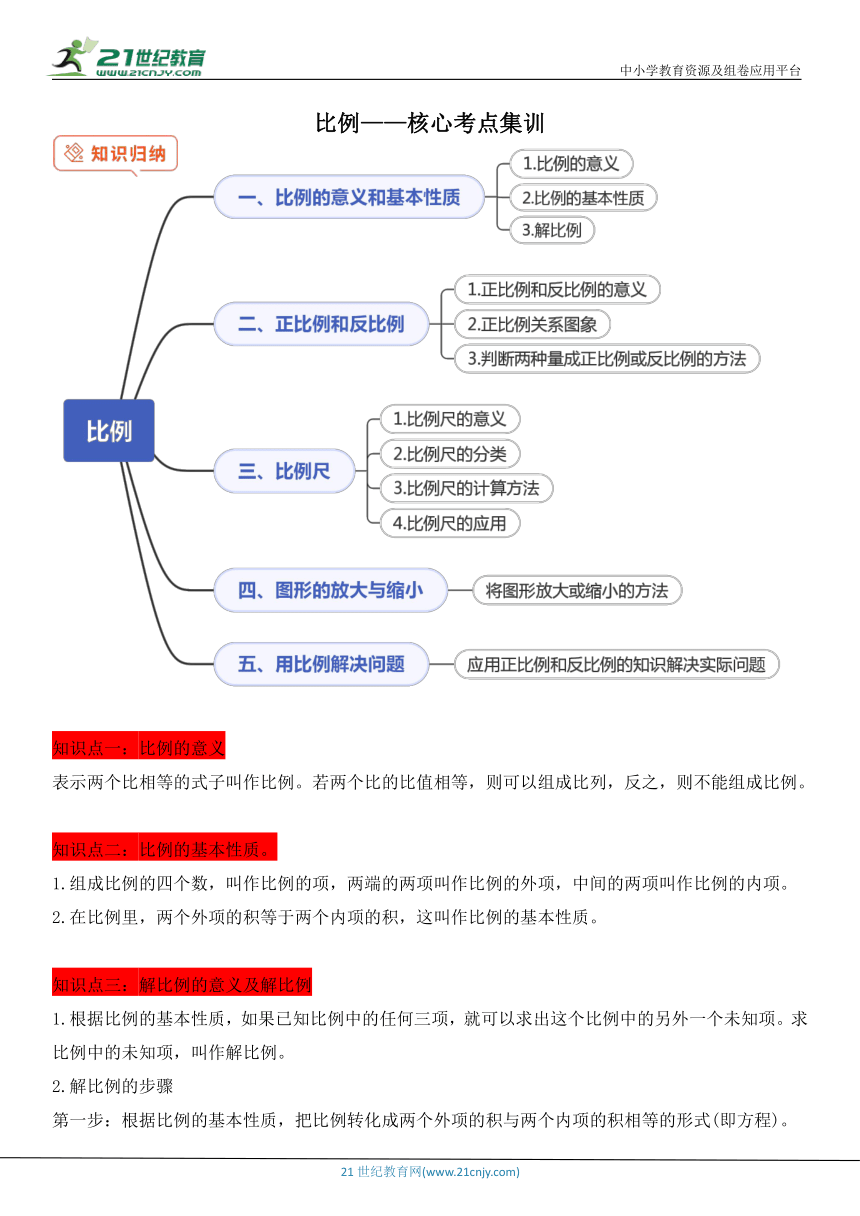
比例——核心考点集训
知识点一:比例的意义
表示两个比相等的式子叫作比例。若两个比的比值相等,则可以组成比列,反之,则不能组成比例。
知识点二:比例的基本性质。
1.组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
知识点三:解比例的意义及解比例
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫作解比例。
2.解比例的步骤
第一步:根据比例的基本性质,把比例转化成两个外项的积与两个内项的积相等的形式(即方程)。
第二步:解方程求出未知项。
知识点四:正比例
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
2.判断两种量成正比例的方法:先看这两种量是不是相关联的量,再看这两种量中相对应的两个数的比值是否一定。
3.正比例关系的图象:正比例关系的图象是一条从(0,0)出发的无限延伸的射线。
知识点五:反比例
1.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
2.判断两种量成反比例的方法:先看这两种量是不是相关联的量,再看这两种量的乘积是否一定。
3.反比例的图象:反比例的两个量也能用描点法表示在图象上,连成线后是一条曲线。
知识点六:比例
1.意义:一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
2.分类:按表现形式分,可以分为数值比例尺和线段比例尺。按将实际距离缩小还是放大来分,可以分为缩小比例尺和放大比例尺。
3.比例尺的应用
(1)已知比例尺和图上距离,求实际距离的方法:①根据“实际距离=图上距离÷比例尺”直接列式计算。②设出未知数,根据“=比例尺"列式解答。
(2)用比例尺画图:①根据实际距离与纸张的大小确定平面图的比例尺。②根据比例尺确定图上距离是多少。③根据图上距离和方向画出相应的平面图并确定平面图的指向标和比列尺。
知识点七:图形的放大与缩小
1.特点:形状相同,大小不同。
2.方法:一看,二算,三画,四总结。
(1)一看:看原图形每边各占几格。
(2)二算:按已知比计算出放大图或缩小图的每边各占几格。
(3)三画:按计算出的边长画出原图形的放大图或缩小图。
(4)要点总结:边长和周长在变化,图形的内角大小不变。
知识点八:用比例解决问题
先根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,再根据正、反比例关系列出相应的方程并求解。
【典例1】用解比例法确定比例的另外一项
在9、5、10这三个数中添上一个数组成比例,这个数可能是( )。
【典例2】解比例
X:(1-)=42: =5:
【典例3】判断两种量成正比例还是反比例
判断表中两种量成什么比例。
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
【典例4】用比例尺解决行程问题
在比例尺是1:60000000的地图上,量得A、B两地之间的距离是6cm,一架飞机下午1时从A地飞往B地,下午5时到达。这架飞机平均每小时飞行多少千米
【典例5】用列比例或抓不变量法解决问题
盒子里有一些黑棋子和白棋子,白棋子和黑棋子的比是2:3,如果从盒子中取出6枚黑棋子,盒子里白棋子和黑棋子的比变成5:6,盒子里原有多少枚黑棋子
【典例6】用比例知识解决与图形面积有关的问题
如图,已知平行四边形的面积是63cm ,图中三角形乙面积是三角形甲的,三角形丙的面积是( )cm 。
1.已知三个数4,6和18,再增加一个数,使这四个数可以组成比例,这个数可以是( )。
①12 ②27 ③3 ④
①②③ B.①②④ C.②③④ D.①②③④
2.解比例。
12:(x-0.6)= =3
3.如果,=,那么A和B( )。
A.成正比例 B.成反比例 C.不成比例 D.不能判断
4.在比例尺为1:10000000的地图上,量得A、B两地之间的距离是6.6 cm。如果小明早上9时从A地乘坐平均时速为220 km的高铁出发,那么他多少小时可以到达B地
5.今年妈妈和小雯的年龄比是5:1,10年后妈妈和小雯的年龄比是5:2,今年妈妈和小雯各多少岁
6.如图,一个平行四边形被两条线段分成四个平行四边形,其中三份的面积分别是12m 、4m 、24m ,图中涂色部分的面积是( )m 。
参考答案
【典例1】用解比例法确定比例的另外一项
在9、5、10这三个数中添上一个数组成比例,这个数可能是( 18 )。
【典例2】用整体思维解较复杂的比例
1.解比例。
X:(1-)=42: =5:
【典例3】判断两种量成正比例还是反比例
判断表中两种量成什么比例。
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
(1)4/1=12/3=24/6=32/8=4 成正比例
(2)2×30=3×20=4×15=5×12=60 成反比例
【典例4】用比例尺解决行程问题
在比例尺是1:60000000的地图上,量得A、B两地之间的距离是6cm,一架飞机下午1时从A地飞往B地,下午5时到达。这架飞机平均每小时飞行多少千米
6÷1/60000000=36000000(cm)
360000000 cm=3600 km
5时-1时=4时
3600÷4=900(km)
【典例5】用列比例或抓不变量法解决问题
盒子里有一些黑棋子和白棋子,白棋子和黑棋子的比是2:3,如果从盒子中取出6枚黑棋子,盒子里白棋子和黑棋子的比变成5:6,盒子里原有多少枚黑棋子
解:设盒子里原有白棋子2x枚,黑棋子3x枚。
2x:(3x-6)=5:6
x=10
3×10=30
答:盒子里原有30枚黑棋子。
【典例6】用比例知识解决与图形面积有关的问题
如图,已知平行四边形的面积是63cm ,图中三角形乙是三角形甲的的面积,三角形丙的面积是( 31.5 )cm 。
1.已知三个数4,6和18,再增加一个数,使这四个数可以组成比例,这个数可以是( B )。
①12 ②27 ③3 ④
①②③ B.①②④ C.②③④ D.①②③④
2.解比例。
12:(x-0.6)= =3
3.如果,=,那么A和B( A )。
A.成正比例 B.成反比例 C.不成比例 D.不能判断
4.在比例尺为1:10000000的地图上,量得A、B两地之间的距离是6.6 cm。如果小明早上9时从A地乘坐平均时速为220 km的高铁出发,那么他多少小时可以到达B地
6.6÷1/10000000=6600000(cm)
66000000cm=660km
660÷220=3(时)
5.今年妈妈和小雯的年龄比是5:1,10年后妈妈和小雯的年龄比是5:2,今年妈妈和小雯各多少岁
解:设小雯今年的年龄是x岁,则妈妈今年的年龄是5x岁。
(5x+10):(x+10)=5:2
x=6
5×6=30
答:今年妈妈30岁,小雯6岁。
6.如图,一个平行四边形被两条线段分成四个平行四边形,其中三份的面积分别是12m 、4m 、24m ,图中涂色部分的面积是( 8 )m 。
知识点一:比例的意义
表示两个比相等的式子叫作比例。若两个比的比值相等,则可以组成比列,反之,则不能组成比例。
知识点二:比例的基本性质。
1.组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
知识点三:解比例的意义及解比例
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫作解比例。
2.解比例的步骤
第一步:根据比例的基本性质,把比例转化成两个外项的积与两个内项的积相等的形式(即方程)。
第二步:解方程求出未知项。
知识点四:正比例
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
2.判断两种量成正比例的方法:先看这两种量是不是相关联的量,再看这两种量中相对应的两个数的比值是否一定。
3.正比例关系的图象:正比例关系的图象是一条从(0,0)出发的无限延伸的射线。
知识点五:反比例
1.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
2.判断两种量成反比例的方法:先看这两种量是不是相关联的量,再看这两种量的乘积是否一定。
3.反比例的图象:反比例的两个量也能用描点法表示在图象上,连成线后是一条曲线。
知识点六:比例
1.意义:一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
2.分类:按表现形式分,可以分为数值比例尺和线段比例尺。按将实际距离缩小还是放大来分,可以分为缩小比例尺和放大比例尺。
3.比例尺的应用
(1)已知比例尺和图上距离,求实际距离的方法:①根据“实际距离=图上距离÷比例尺”直接列式计算。②设出未知数,根据“=比例尺"列式解答。
(2)用比例尺画图:①根据实际距离与纸张的大小确定平面图的比例尺。②根据比例尺确定图上距离是多少。③根据图上距离和方向画出相应的平面图并确定平面图的指向标和比列尺。
知识点七:图形的放大与缩小
1.特点:形状相同,大小不同。
2.方法:一看,二算,三画,四总结。
(1)一看:看原图形每边各占几格。
(2)二算:按已知比计算出放大图或缩小图的每边各占几格。
(3)三画:按计算出的边长画出原图形的放大图或缩小图。
(4)要点总结:边长和周长在变化,图形的内角大小不变。
知识点八:用比例解决问题
先根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,再根据正、反比例关系列出相应的方程并求解。
【典例1】用解比例法确定比例的另外一项
在9、5、10这三个数中添上一个数组成比例,这个数可能是( )。
【典例2】解比例
X:(1-)=42: =5:
【典例3】判断两种量成正比例还是反比例
判断表中两种量成什么比例。
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
【典例4】用比例尺解决行程问题
在比例尺是1:60000000的地图上,量得A、B两地之间的距离是6cm,一架飞机下午1时从A地飞往B地,下午5时到达。这架飞机平均每小时飞行多少千米
【典例5】用列比例或抓不变量法解决问题
盒子里有一些黑棋子和白棋子,白棋子和黑棋子的比是2:3,如果从盒子中取出6枚黑棋子,盒子里白棋子和黑棋子的比变成5:6,盒子里原有多少枚黑棋子
【典例6】用比例知识解决与图形面积有关的问题
如图,已知平行四边形的面积是63cm ,图中三角形乙面积是三角形甲的,三角形丙的面积是( )cm 。
1.已知三个数4,6和18,再增加一个数,使这四个数可以组成比例,这个数可以是( )。
①12 ②27 ③3 ④
①②③ B.①②④ C.②③④ D.①②③④
2.解比例。
12:(x-0.6)= =3
3.如果,=,那么A和B( )。
A.成正比例 B.成反比例 C.不成比例 D.不能判断
4.在比例尺为1:10000000的地图上,量得A、B两地之间的距离是6.6 cm。如果小明早上9时从A地乘坐平均时速为220 km的高铁出发,那么他多少小时可以到达B地
5.今年妈妈和小雯的年龄比是5:1,10年后妈妈和小雯的年龄比是5:2,今年妈妈和小雯各多少岁
6.如图,一个平行四边形被两条线段分成四个平行四边形,其中三份的面积分别是12m 、4m 、24m ,图中涂色部分的面积是( )m 。
参考答案
【典例1】用解比例法确定比例的另外一项
在9、5、10这三个数中添上一个数组成比例,这个数可能是( 18 )。
【典例2】用整体思维解较复杂的比例
1.解比例。
X:(1-)=42: =5:
【典例3】判断两种量成正比例还是反比例
判断表中两种量成什么比例。
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
(1)4/1=12/3=24/6=32/8=4 成正比例
(2)2×30=3×20=4×15=5×12=60 成反比例
【典例4】用比例尺解决行程问题
在比例尺是1:60000000的地图上,量得A、B两地之间的距离是6cm,一架飞机下午1时从A地飞往B地,下午5时到达。这架飞机平均每小时飞行多少千米
6÷1/60000000=36000000(cm)
360000000 cm=3600 km
5时-1时=4时
3600÷4=900(km)
【典例5】用列比例或抓不变量法解决问题
盒子里有一些黑棋子和白棋子,白棋子和黑棋子的比是2:3,如果从盒子中取出6枚黑棋子,盒子里白棋子和黑棋子的比变成5:6,盒子里原有多少枚黑棋子
解:设盒子里原有白棋子2x枚,黑棋子3x枚。
2x:(3x-6)=5:6
x=10
3×10=30
答:盒子里原有30枚黑棋子。
【典例6】用比例知识解决与图形面积有关的问题
如图,已知平行四边形的面积是63cm ,图中三角形乙是三角形甲的的面积,三角形丙的面积是( 31.5 )cm 。
1.已知三个数4,6和18,再增加一个数,使这四个数可以组成比例,这个数可以是( B )。
①12 ②27 ③3 ④
①②③ B.①②④ C.②③④ D.①②③④
2.解比例。
12:(x-0.6)= =3
3.如果,=,那么A和B( A )。
A.成正比例 B.成反比例 C.不成比例 D.不能判断
4.在比例尺为1:10000000的地图上,量得A、B两地之间的距离是6.6 cm。如果小明早上9时从A地乘坐平均时速为220 km的高铁出发,那么他多少小时可以到达B地
6.6÷1/10000000=6600000(cm)
66000000cm=660km
660÷220=3(时)
5.今年妈妈和小雯的年龄比是5:1,10年后妈妈和小雯的年龄比是5:2,今年妈妈和小雯各多少岁
解:设小雯今年的年龄是x岁,则妈妈今年的年龄是5x岁。
(5x+10):(x+10)=5:2
x=6
5×6=30
答:今年妈妈30岁,小雯6岁。
6.如图,一个平行四边形被两条线段分成四个平行四边形,其中三份的面积分别是12m 、4m 、24m ,图中涂色部分的面积是( 8 )m 。
