人教版八年级数学下册 第17章 运用勾股定理解决最短路径问题 练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册 第17章 运用勾股定理解决最短路径问题 练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 742.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 14:44:44 | ||
图片预览


文档简介
第17章《勾股定理》--运用勾股定理解决最短路径问题
【题型1 正方体中的最短路径】
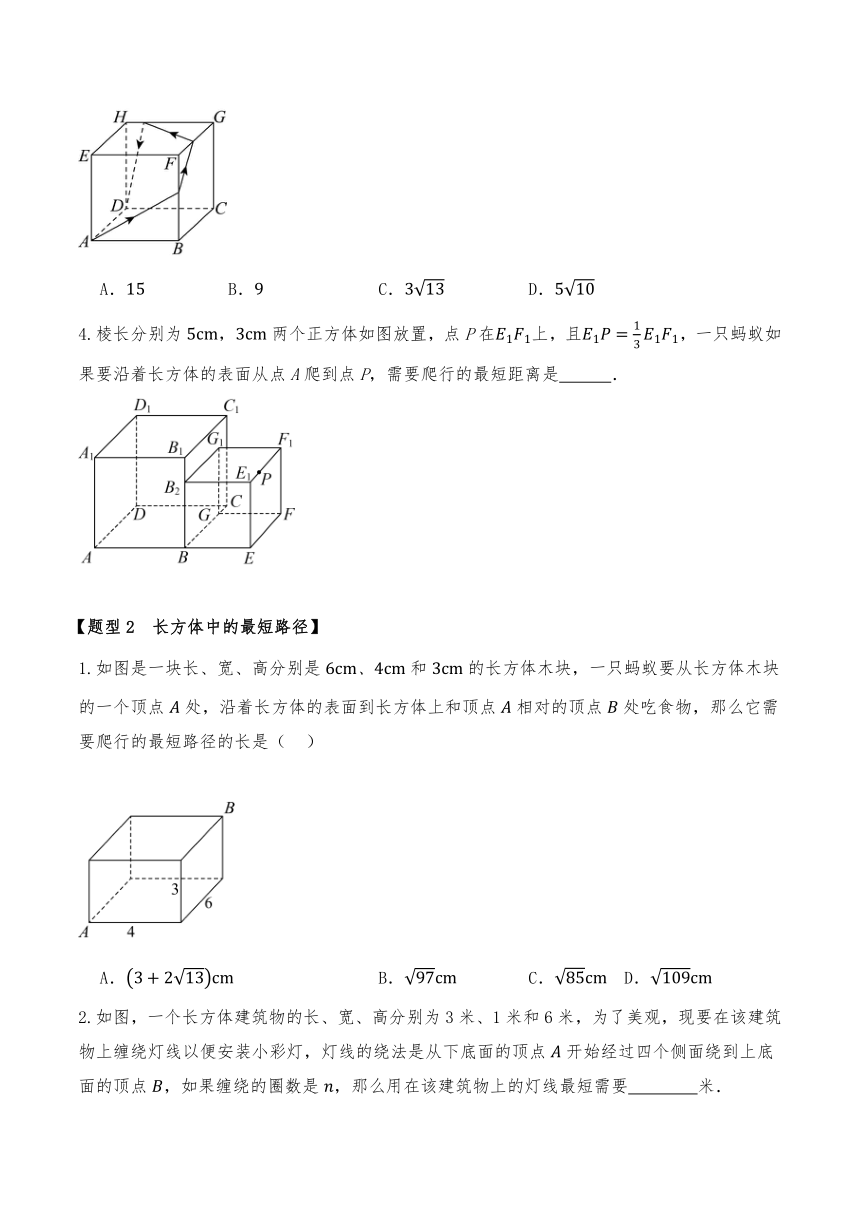
1.如图,在棱长为的正方体上有一些线段,把所有的面都分成9个小正方形,每个小正方形的边长都为.若一只蚂蚁每秒爬行,则它从下底面点沿表面爬行至右侧点最少要花多长时间?
2.如图,正方体盒子的棱长为2,M为的中点,则一只蚂蚁从M点沿盒子的表面爬行到A点的最短距离为( )
A. B. C. D.
3.如图,有一棱长为的正方体盒子,现要按图中箭头所指方向从点到点拉一条捆绑线绳,使线绳经过、、、四个面,则所需捆绑线绳的长至少为( ).
A. B. C. D.
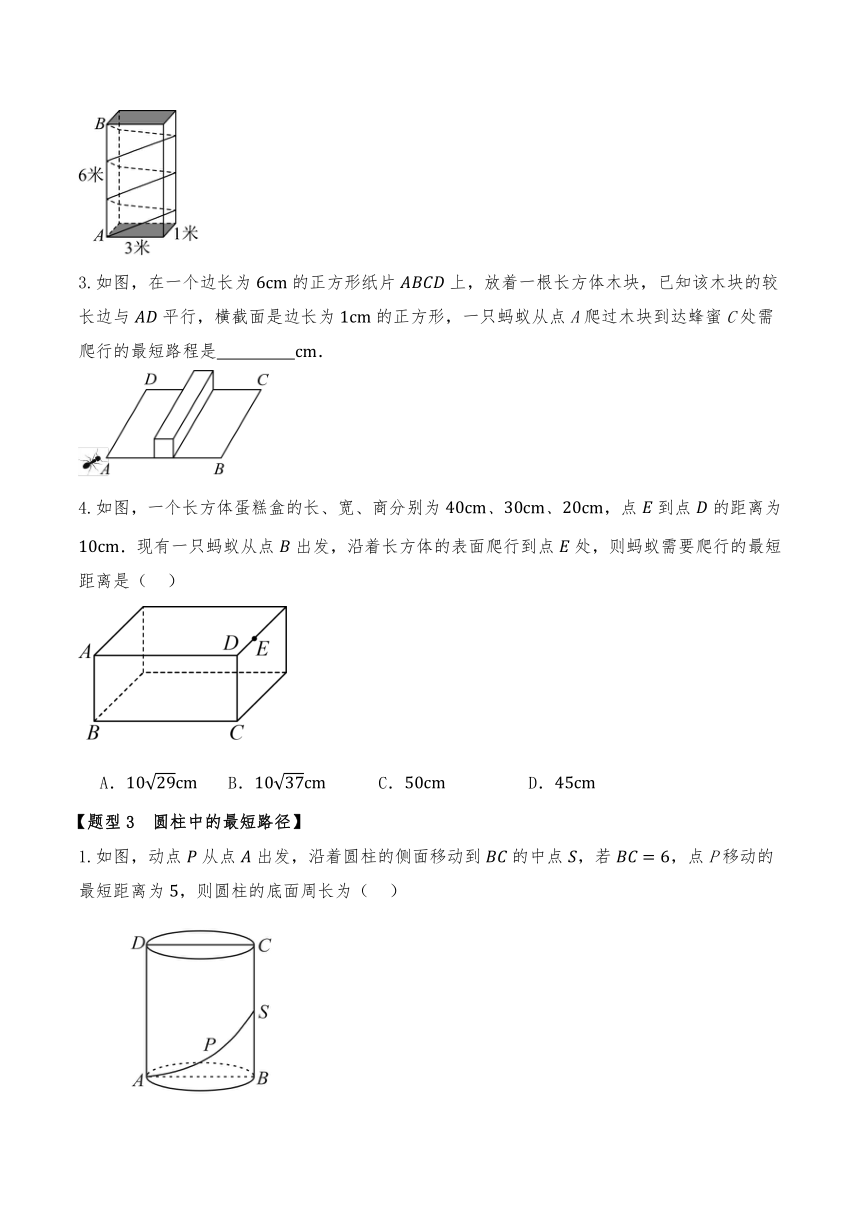
4.棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是 .
【题型2 长方体中的最短路径】
1.如图是一块长、宽、高分别是和的长方体木块,一只蚂蚁要从长方体木块的一个顶点处,沿着长方体的表面到长方体上和顶点相对的顶点处吃食物,那么它需要爬行的最短路径的长是( )
A. B. C. D.
2.如图,一个长方体建筑物的长、宽、高分别为3米、1米和6米,为了美观,现要在该建筑物上缠绕灯线以便安装小彩灯,灯线的绕法是从下底面的顶点开始经过四个侧面绕到上底面的顶点,如果缠绕的圈数是,那么用在该建筑物上的灯线最短需要 米.
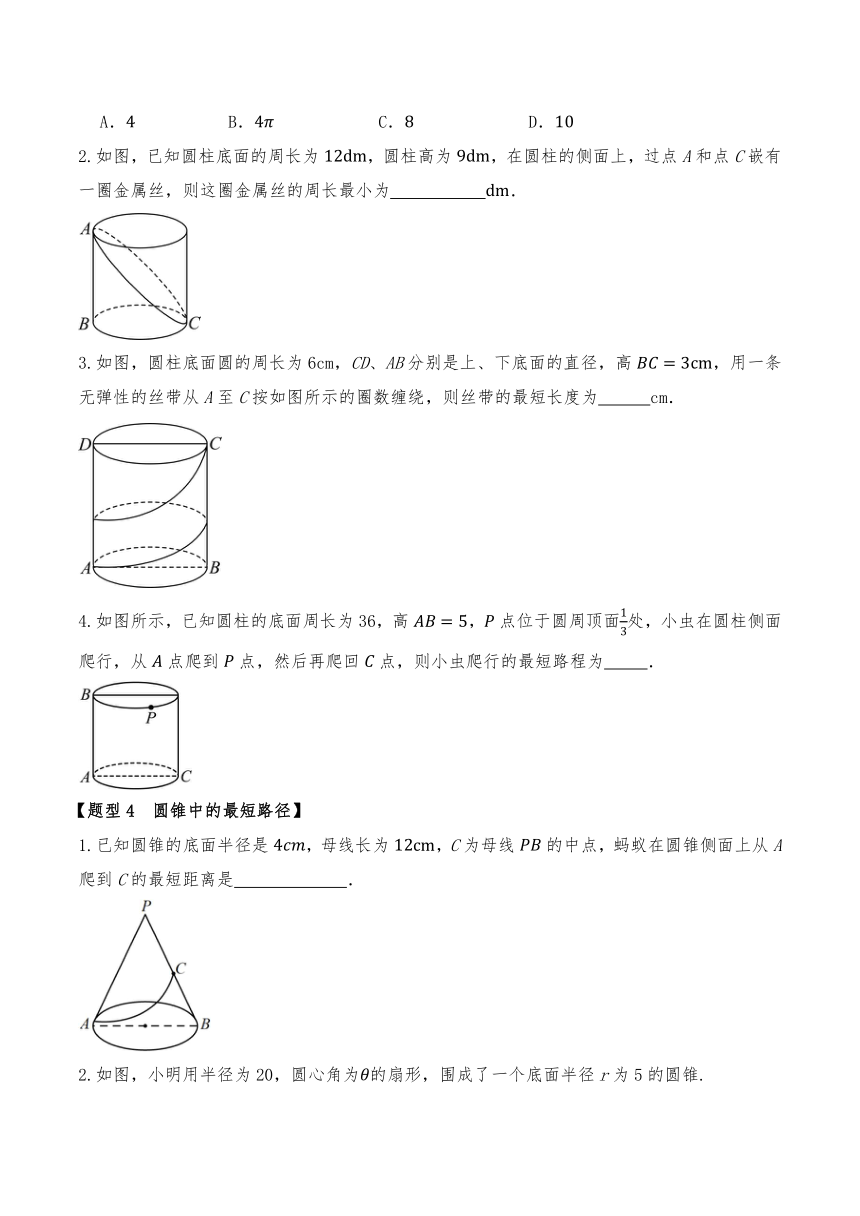
3.如图,在一个边长为的正方形纸片上,放着一根长方体木块,已知该木块的较长边与平行,横截面是边长为的正方形,一只蚂蚁从点A爬过木块到达蜂蜜C处需爬行的最短路程是 .
4.如图,一个长方体蛋糕盒的长、宽、商分别为,点到点的距离为.现有一只蚂蚁从点出发,沿着长方体的表面爬行到点处,则蚂蚁需要爬行的最短距离是( )
A. B. C. D.
【题型3 圆柱中的最短路径】
1.如图,动点从点出发,沿着圆柱的侧面移动到的中点,若,点P移动的最短距离为,则圆柱的底面周长为( )
A. B. C. D.
2.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 .
3.如图,圆柱底面圆的周长为6cm,CD、AB分别是上、下底面的直径,高,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm.
4.如图所示,已知圆柱的底面周长为36,高,点位于圆周顶面处,小虫在圆柱侧面爬行,从点爬到点,然后再爬回点,则小虫爬行的最短路程为 .
【题型4 圆锥中的最短路径】
1.已知圆锥的底面半径是,母线长为,C为母线的中点,蚂蚁在圆锥侧面上从A爬到C的最短距离是 .
2.如图,小明用半径为20,圆心角为的扇形,围成了一个底面半径r为5的圆锥.
(1)扇形的圆心角为 ;
(2)一只蜘蛛从圆锥底面圆周上一点A出发,沿圆锥的侧面爬行一周后回到点A的最短路程是 .
3.某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 ,母线长为30,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
A. B. C. D.
4.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( )
A. B.2 C.3 D.4
【题型5 台阶中的最短路径】
1.如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是台阶两个相对的端点,在点有一只蚂蚁,想到点去觅食,那么它爬行的最短路程是( )
A. B. C. D.
2.如图,学校实验楼前一个三级台阶,它的每—级的长、宽、高分别为24dm,3dm,3dm,点M和点N是这个台阶上两个相对的端点,M点有一只蚂蚁,想到N点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点N的最短路程( )
A. B. C. D.
3.如图,是一个三级台阶,它每一级长,宽,高分别为4, 和 ,和是这个台阶的两个相对的端点,点上有一只蚂蚁想到点去吃可口的食物,则它所走的最短路线长度为( )
A.3.5 B.4.5 C.5 D.5.5
4.如图,这是一个台阶的示意图,每一层台阶的高是、长是、宽是,一只蚂蚁沿台阶从点出发爬到点,其爬行的最短线路的长度是 .
【题型6 由垂线段最短求最短路径】
1.如图,中,,,点,分别是、的中点,在上找一点,连接、,当最小时,这个最小值是 .
2.如下图,某国道通过A、B两个村庄,而C村庄离国道较远,为了相应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道,已知C村到A、B两村的距离分别为、,A,B两村的距离为,那么这条水泥路的最短距离为多少?
3.如图A,B,C为三个村庄,A,B两村沿河而建且相距17千米,A,C相距千米,B,C相距13千米,C村需从河边修建一条引水渠到村庄,每千米造价1.5万元,则费用最低为( )万元
A.6 B. C.4.5 D.7.5
4.如图,在中,,,,,平分交于D点,E,F分别是,上的动点,则的最小值为 .
【题型7 由将军饮马求最短路径】
1.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路径是 km.
2.如图,河的同侧有、两个村,且,、两村到河的距离分别为,.现要在河边上建一水厂分别向、两村输送自来水,铺设水管的工程费每千米需2000元.请你在河岸上选择水厂位置,使铺设水管的费用最省,并求出铺设水管的总费用(元).
3.如图,已知直线,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,,试在直线a上找一点M,在直线b上找一点N,满足且的长度和最短,则此时 .
【题型8 不规则图形中求最短路径】
1.如图,教室墙面与地面垂直,点P在墙面上,若米,米,点到的距离是米,一只蚂蚁要从点爬到点,它的最短行程是( )米
A. B. C.5 D.
2.在一个长11cm,宽5cm的长方形纸片上,如图放置一根正三棱柱的木块,它的侧棱平行且大于纸片的宽,它的底面边长为1cm的等边三角形,一只蚂蚁从点A处到点C处的最短路程是 cm.
3.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的截面是半径为4的半圆,其边缘,点E在上,,一滑行爱好者从点滑行到点,则他滑行的最短距离为 (π的值为3).
4.固定在地面上的一个正方体木块如图①所示,其棱长为4,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点爬行到点的最短路程为( )
A. B. C. D.
参考答案
【题型1 正方体中的最短路径】
1.解:如图所示,分两种情况讨论:
①如图1,将正方体的正前和右侧两面展开,使点,在同一平面内.则点到点的最短路径是线段,
由题意,得,,
根据勾股定理,得;
②如图2,将正方体的正前和上底两面展开,使点,在同一平面内,则点到点的最短路径为线段,
由题意,得,,
根据勾股定理.得.
∵,
∴图1中的路径最短,
∴这只蚂蚁至少要爬行的时间为.
2.B
【分析】本题考查了两点之间线段最短、正方体的展开图、勾股定理等知识,先利用展开图确定最短路径,再由勾股定理求解即可,牢记相关概念和灵活应用是解题的关键.
【详解】解:如图,蚂蚁沿路线爬行路程最短,
,为的中点,
,
.
故选:.
3.C
【分析】此题考查了勾股定理的应用,把此正方体的一面展开,然后在平面内,利用勾股定理求点和点间的线段长,即可得到捆绑线绳的最短距离.在直角三角形中,一条直角边长等于两个棱长,另一条直角边长等于个棱长,利用勾股定理可求得,“化曲面为平面”是解决“怎样爬行最近”解题的关键.
【详解】如图,将正方体展开,根据“两点之间,线段最短”知,线段即为最短路线,
展开后由勾股定理得:,
∴,即有:,
故选:.
4.cm.
【分析】求出两种展开图的值,比较即可判断;
【详解】解:如图,有两种展开方法:
方法一∶,
方法二∶.
故需要爬行的最短距离是cm.
故答案为:cm.
【题型2 长方体中的最短路径】
1.C
【分析】展成平面图形,根据两点之间线段最短,可求出解.本题考查平面展开路径问题、勾股定理,本题关键知道蚂蚁爬行的路线不同,求出的值就不同,有三种情况,可求出值找到最短路线.
【详解】解:就是蚂蚁爬的最短路线.
但有三种情况:
当:,.
.
当,.
.
当,
.
∵
∴第三种情况最短.
故选:C.
2.
【分析】本题主要考查最短路径问题,画出展开图,运用勾股定理求解即可.
【详解】解:如图,
米,米,
由勾股定理得,(米);
故答案为:.
3.
【分析】本题考查了勾股定理在最短路径中的应用,将长方体侧面展开得蚂蚁的爬行的最短路径为的长,用勾股定理即可求解;能找出最短路径是解题的关键.
【详解】解:如图,将长方体侧面展开得,
蚂蚁的爬行的最短路径为的长,
(),
,
蚂蚁的爬行的最短路径为 ,
故答案:.
4.C
【分析】考虑蚂蚁从正面和上面沿直线爬到点,从正面和右侧面沿直线爬到点,从左侧面和上面沿直线爬到点,画出图形,利用勾股定理求出距离,进行比较即可解答.
【详解】解:当蚂蚁从正面和上面沿直线爬到点,如图所示:
此时,则,
;
当蚂蚁从正面和右侧面沿直线爬到点,如图所示:
此时,则,
;
从左侧面和上面沿直线爬到点,如图所示:
此时,则,
;
,
蚂蚁需要爬行的报短距离是,
故选:C.
【题型3 圆柱中的最短路径】
1.C
【分析】本题考查平面展开—最短路径问题,先根据题意画出圆柱的侧面展开图,然后连接,再利用勾股定理即可得出的长即可得到结论.利用勾股定理求解是解题的关键.
【详解】解:如图,连接,
在圆柱的侧面展开图中,,,设,
∵点移动的最短距离为,
∴,
∵点是的中点,
∴,
∴,
∴圆柱的底面周长为:.
故选:C.
2.
【分析】本题考查了平面展开﹣最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
【详解】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
∵圆柱底面的周长为,圆柱高为,
∴,
∴,
∴,
∴这圈金属丝的周长最小为.
故答案为:.
3.
【分析】本题考查了平面展开-最短路线问题和勾股定理的应用,把立体图形展开成平面图形,依题意,从A到C缠绕了一圈半,则,,根据两点之间线段最短求出长即可解决问题.
【详解】解:如图所示,
∵无弹性的丝带从A至C,绕了1.5圈,
∴展开后,,
由勾股定理得:
故答案为:.
4.
【分析】本题主要考查了平面展开图最短路径问题,先“化曲面为平面”,把圆柱的侧面展开成矩形,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.再根据两点之间线段最短,由勾股定理可得出.
【详解】解:如图,
根据题意,, ,
∵点位于圆周顶面处,
∴,,
∴小虫爬行的最短路程.
故选:.
【题型4 圆锥中的最短路径】
1.
【分析】根据题意可得圆锥的底面周长是,即可得圆锥侧面展开图的圆心角是,展开圆锥的侧面,构造直角三角形即可得.
【详解】解:圆锥的底面周长是:,
则
,
即圆锥侧面展开图的圆心角是,
如图所示,
∴,
∵,
∴是等边三角形,
∵C是的中点,
∴,
∴,
∵在圆锥侧面展开图中,,
∴在圆锥侧面展开图中:,
∴蚂蚁在圆锥侧面上从A爬到C的最短距离是:,
故答案为:.
2.
【分析】(1)由于圆锥的底面圆周长就是圆锥的侧面展开图的弧长,利用弧长公式即可求出侧面展开图的圆心角;
(2)根据两点之间线段最短,把圆锥的侧面展开成平面图形,构造直角三角形根据勾股定理即可求得.
【详解】解(1)圆锥的底面周长,
,
解得;
故答案为.
(2)圆锥的侧面展开图如图所示,构造,根据两点之间线段最短得最短路程为:.
故答案为.
3.B
【分析】根据圆锥的底面圆周长求得半径为,根据母线长求得展开后的扇形的圆心角为,进而即可求解.
【详解】解:∵这个圆锥的底面圆周长为 ,
∴
解得:
∵
解得:
∴侧面展开图的圆心角为
如图所示,即为所求,过点作,
∵,,则
∵,则
∴,,
故选:B.
4.C
【分析】求出圆锥底面圆的周长,则以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,根据弧长公式求出展开后扇形的圆心角,求出展开后∠BAC=90°,连接BP,根据勾股定理求出BP即可.
【详解】圆锥底面是以BC为直径的圆,圆的周长是 6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则
解得:n=180,
即展开后
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:
故选C.
【题型5 台阶中的最短路径】
1.C
【分析】本题考查平面展开—最短路径问题,勾股定理.根据题意画出台阶的侧面展开图,再根据勾股定理求出的长即可得出结论.
【详解】解:如图所示,
,
.
故选C.
2.C
【分析】本题考查的是平面展开-最短路线问题,根据题意画出台阶的平面展开图,再用勾股定理根据两点之间线段最短进行解答.
【详解】解:如图所示,
∵它的每一级的长宽高分别为,
∴
即:蚂蚁沿着台阶面爬行到点N的最短路程是,
故选:C.
3.C
【分析】本题主要考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.将台阶展开为矩形,然后利用勾股定理计算的值,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】解:如下图,将台阶展开为矩形,线段恰好是直角三角形的斜边,
则,,
在中,,
所以蚂蚁所走的最短路线长度为5.
故选:C.
4.
【分析】展开成平面图形,根据勾股定理,即可求解,本题考查了勾股定理的应用,解题的关键是:利用两点之间线段最短.
【详解】解:将台阶展开成平面图形:
在中,,,
,
其爬行的最短长度,
故答案为:.
【题型6 由垂线段最短求最短路径】
1.
【分析】连接,BP,根据等腰三角形的性质可得CD垂直平分AB,从而得到AP=BP,进而得到就是的最小值,再由勾股定理求出BE,即可求解.
【详解】解:如图,连接,BP,
∵,点是的中点,
∴CD垂直平分AB,
∴AP=BP,
∴AP+PE=BP+PE≥BE,
∴就是的最小值,
∵中,,点,分别是,的中点,
∴,
∴,
∴的最小值是.
故答案为:.
2.解:过点C作,垂足为D点,
则这条水泥路的最短距离为的长度,
,
在中,,,,
则,即:,
∴为直角三角形,
∴,
这条水泥路的最短距离为.
3.D
【分析】本题主要考查了勾股定理,正确理解勾股定理的含义是解题关键.过点C作,设千米,则千米,由勾股定理可得,列出方程求解,再用勾股定理求出即可得出答案.
【详解】如图,过点C作,
设千米,则千米,
,
,
,
,
千米,
(千米),
费用最低为万元.
故选:D
4.
【分析】本题主要考查的是轴对称的性质、勾股定理的应用、垂线段最短等知识,解题的关键是学利用对称,解决最短问题.
如图所示:在上取点,使,过点C作,垂足为H.因为,推出当C、E、共线,且点与H重合时,的值最小.
【详解】解:如图所示:在上取点,使,
∵,
∴,
∴.
在中,
.
过点C作,垂足为H.
,
,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为的长,
的值最小为,
故答案为:.
【题型7 由将军饮马求最短路径】
1.17
【分析】如图(见详解),将小河看成直线MN,由题意先作A关于MN的对称点,连接A`B,构建直角三角形,则A`B就是最短路线;在Rt△A`DB中,∠A`DB=90°,BD=8km,A`D=AD+A`A,利用勾股定理即可求出A`B.
【详解】如图,做出点A关于小河MN的对称点A`,连接A`B交MN于点P,则A`B就是牧童要完成这件事情所走的最短路程长度.
在Rt△A`DB中,由勾股定理求得.
则他要完成这件事情所走的最短路程是17km.
2.解:如图,作点关于的对称点,连接交于,点即为水厂的位置.
分过点作交的延长线于点,过点作于点,
则,,.
∴.
在中,,
∴,
∴.
在中,,
由勾股定理得.
∴(元).
故铺设水管的总费用为20000元.
3.
【分析】表示直线与直线之间的距离,是定值,只要满足的值最小即可.过作直线的垂线,并在此垂线上取点,使得,连接,则与直线的交点即为,过作于点.则为所求,利用勾股定理可求得其值.
【详解】解:过作直线的垂线,并在此垂线上取点,使得,连接,与直线交于点,过作直线的垂线,交直线于点,连接,过点作,交射线于点,如图.
,,
.
又,
四边形是平行四边形,
.
由于要最小,且固定为4,所以最小.
由两点之间线段最短,可知的最小值为.
,,
,
,
所以的最小值为.
故答案为:.
【题型8 不规则图形中求最短路径】
1.C
【分析】本题考查平面展开—最短路径问题及勾股定理的应用,可将教室的墙面与地面展开,连接,根据两点之间线段最短,利用勾股定理求解即可.正确利用立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决是解题的关键.
【详解】解:如图,过作于,连接,
此时的长为这只蚂蚁从点爬到点的最短行程,
∵米,米,点到的距离是米,
∴米,
∴(米),
∴(米),
∴(米),
∴这只蚂蚁的最短行程应该是米.
故选:C.
2.13
【分析】将木块展开看作平面后,由两点之间线段最短知蚂蚁的最短距离为线段AC,由勾股定理计算即可.
【详解】将长方形纸片与木块展开后如图所示
由两点之间线段最短可知蚂蚁的最短距离为线段AC
此时AB长度为11-1+2=12
由勾股定理有
即
故答案为:13.
3.20
【分析】本题主要考查了勾股定理的应用—最短路径问题.通过将U型池的侧面展开成矩形,“化曲面为平面”,用勾股定理求最短路径是解题的关键.将半圆面展开,连接,则是最短路径,根据,计算求解即可.
【详解】解:将半圆面展开如图:连接,则是最短路径,
∴,,
由勾股定理得,.
∴滑行的最短距离约为,
故答案为:20.
4.A
【分析】本题考查勾股定理的应用.根据两点之间线段最短,将图②展开,利用勾股定理进行求解即可.
【详解】解:如图,正方体上表面的对角线为,将图②展开,连接交于点,线段的长度即为蚂蚁爬行的最短路程,
由题意可知:为等边三角形,为等腰直角三角形,
,,,
,
,
,
正方体的棱长为4,
,,
在中,,
在中,,
.
故选:A.
【题型1 正方体中的最短路径】
1.如图,在棱长为的正方体上有一些线段,把所有的面都分成9个小正方形,每个小正方形的边长都为.若一只蚂蚁每秒爬行,则它从下底面点沿表面爬行至右侧点最少要花多长时间?
2.如图,正方体盒子的棱长为2,M为的中点,则一只蚂蚁从M点沿盒子的表面爬行到A点的最短距离为( )
A. B. C. D.
3.如图,有一棱长为的正方体盒子,现要按图中箭头所指方向从点到点拉一条捆绑线绳,使线绳经过、、、四个面,则所需捆绑线绳的长至少为( ).
A. B. C. D.
4.棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是 .
【题型2 长方体中的最短路径】
1.如图是一块长、宽、高分别是和的长方体木块,一只蚂蚁要从长方体木块的一个顶点处,沿着长方体的表面到长方体上和顶点相对的顶点处吃食物,那么它需要爬行的最短路径的长是( )
A. B. C. D.
2.如图,一个长方体建筑物的长、宽、高分别为3米、1米和6米,为了美观,现要在该建筑物上缠绕灯线以便安装小彩灯,灯线的绕法是从下底面的顶点开始经过四个侧面绕到上底面的顶点,如果缠绕的圈数是,那么用在该建筑物上的灯线最短需要 米.
3.如图,在一个边长为的正方形纸片上,放着一根长方体木块,已知该木块的较长边与平行,横截面是边长为的正方形,一只蚂蚁从点A爬过木块到达蜂蜜C处需爬行的最短路程是 .
4.如图,一个长方体蛋糕盒的长、宽、商分别为,点到点的距离为.现有一只蚂蚁从点出发,沿着长方体的表面爬行到点处,则蚂蚁需要爬行的最短距离是( )
A. B. C. D.
【题型3 圆柱中的最短路径】
1.如图,动点从点出发,沿着圆柱的侧面移动到的中点,若,点P移动的最短距离为,则圆柱的底面周长为( )
A. B. C. D.
2.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 .
3.如图,圆柱底面圆的周长为6cm,CD、AB分别是上、下底面的直径,高,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm.
4.如图所示,已知圆柱的底面周长为36,高,点位于圆周顶面处,小虫在圆柱侧面爬行,从点爬到点,然后再爬回点,则小虫爬行的最短路程为 .
【题型4 圆锥中的最短路径】
1.已知圆锥的底面半径是,母线长为,C为母线的中点,蚂蚁在圆锥侧面上从A爬到C的最短距离是 .
2.如图,小明用半径为20,圆心角为的扇形,围成了一个底面半径r为5的圆锥.
(1)扇形的圆心角为 ;
(2)一只蜘蛛从圆锥底面圆周上一点A出发,沿圆锥的侧面爬行一周后回到点A的最短路程是 .
3.某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 ,母线长为30,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
A. B. C. D.
4.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( )
A. B.2 C.3 D.4
【题型5 台阶中的最短路径】
1.如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是台阶两个相对的端点,在点有一只蚂蚁,想到点去觅食,那么它爬行的最短路程是( )
A. B. C. D.
2.如图,学校实验楼前一个三级台阶,它的每—级的长、宽、高分别为24dm,3dm,3dm,点M和点N是这个台阶上两个相对的端点,M点有一只蚂蚁,想到N点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点N的最短路程( )
A. B. C. D.
3.如图,是一个三级台阶,它每一级长,宽,高分别为4, 和 ,和是这个台阶的两个相对的端点,点上有一只蚂蚁想到点去吃可口的食物,则它所走的最短路线长度为( )
A.3.5 B.4.5 C.5 D.5.5
4.如图,这是一个台阶的示意图,每一层台阶的高是、长是、宽是,一只蚂蚁沿台阶从点出发爬到点,其爬行的最短线路的长度是 .
【题型6 由垂线段最短求最短路径】
1.如图,中,,,点,分别是、的中点,在上找一点,连接、,当最小时,这个最小值是 .
2.如下图,某国道通过A、B两个村庄,而C村庄离国道较远,为了相应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道,已知C村到A、B两村的距离分别为、,A,B两村的距离为,那么这条水泥路的最短距离为多少?
3.如图A,B,C为三个村庄,A,B两村沿河而建且相距17千米,A,C相距千米,B,C相距13千米,C村需从河边修建一条引水渠到村庄,每千米造价1.5万元,则费用最低为( )万元
A.6 B. C.4.5 D.7.5
4.如图,在中,,,,,平分交于D点,E,F分别是,上的动点,则的最小值为 .
【题型7 由将军饮马求最短路径】
1.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路径是 km.
2.如图,河的同侧有、两个村,且,、两村到河的距离分别为,.现要在河边上建一水厂分别向、两村输送自来水,铺设水管的工程费每千米需2000元.请你在河岸上选择水厂位置,使铺设水管的费用最省,并求出铺设水管的总费用(元).
3.如图,已知直线,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,,试在直线a上找一点M,在直线b上找一点N,满足且的长度和最短,则此时 .
【题型8 不规则图形中求最短路径】
1.如图,教室墙面与地面垂直,点P在墙面上,若米,米,点到的距离是米,一只蚂蚁要从点爬到点,它的最短行程是( )米
A. B. C.5 D.
2.在一个长11cm,宽5cm的长方形纸片上,如图放置一根正三棱柱的木块,它的侧棱平行且大于纸片的宽,它的底面边长为1cm的等边三角形,一只蚂蚁从点A处到点C处的最短路程是 cm.
3.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的截面是半径为4的半圆,其边缘,点E在上,,一滑行爱好者从点滑行到点,则他滑行的最短距离为 (π的值为3).
4.固定在地面上的一个正方体木块如图①所示,其棱长为4,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点爬行到点的最短路程为( )
A. B. C. D.
参考答案
【题型1 正方体中的最短路径】
1.解:如图所示,分两种情况讨论:
①如图1,将正方体的正前和右侧两面展开,使点,在同一平面内.则点到点的最短路径是线段,
由题意,得,,
根据勾股定理,得;
②如图2,将正方体的正前和上底两面展开,使点,在同一平面内,则点到点的最短路径为线段,
由题意,得,,
根据勾股定理.得.
∵,
∴图1中的路径最短,
∴这只蚂蚁至少要爬行的时间为.
2.B
【分析】本题考查了两点之间线段最短、正方体的展开图、勾股定理等知识,先利用展开图确定最短路径,再由勾股定理求解即可,牢记相关概念和灵活应用是解题的关键.
【详解】解:如图,蚂蚁沿路线爬行路程最短,
,为的中点,
,
.
故选:.
3.C
【分析】此题考查了勾股定理的应用,把此正方体的一面展开,然后在平面内,利用勾股定理求点和点间的线段长,即可得到捆绑线绳的最短距离.在直角三角形中,一条直角边长等于两个棱长,另一条直角边长等于个棱长,利用勾股定理可求得,“化曲面为平面”是解决“怎样爬行最近”解题的关键.
【详解】如图,将正方体展开,根据“两点之间,线段最短”知,线段即为最短路线,
展开后由勾股定理得:,
∴,即有:,
故选:.
4.cm.
【分析】求出两种展开图的值,比较即可判断;
【详解】解:如图,有两种展开方法:
方法一∶,
方法二∶.
故需要爬行的最短距离是cm.
故答案为:cm.
【题型2 长方体中的最短路径】
1.C
【分析】展成平面图形,根据两点之间线段最短,可求出解.本题考查平面展开路径问题、勾股定理,本题关键知道蚂蚁爬行的路线不同,求出的值就不同,有三种情况,可求出值找到最短路线.
【详解】解:就是蚂蚁爬的最短路线.
但有三种情况:
当:,.
.
当,.
.
当,
.
∵
∴第三种情况最短.
故选:C.
2.
【分析】本题主要考查最短路径问题,画出展开图,运用勾股定理求解即可.
【详解】解:如图,
米,米,
由勾股定理得,(米);
故答案为:.
3.
【分析】本题考查了勾股定理在最短路径中的应用,将长方体侧面展开得蚂蚁的爬行的最短路径为的长,用勾股定理即可求解;能找出最短路径是解题的关键.
【详解】解:如图,将长方体侧面展开得,
蚂蚁的爬行的最短路径为的长,
(),
,
蚂蚁的爬行的最短路径为 ,
故答案:.
4.C
【分析】考虑蚂蚁从正面和上面沿直线爬到点,从正面和右侧面沿直线爬到点,从左侧面和上面沿直线爬到点,画出图形,利用勾股定理求出距离,进行比较即可解答.
【详解】解:当蚂蚁从正面和上面沿直线爬到点,如图所示:
此时,则,
;
当蚂蚁从正面和右侧面沿直线爬到点,如图所示:
此时,则,
;
从左侧面和上面沿直线爬到点,如图所示:
此时,则,
;
,
蚂蚁需要爬行的报短距离是,
故选:C.
【题型3 圆柱中的最短路径】
1.C
【分析】本题考查平面展开—最短路径问题,先根据题意画出圆柱的侧面展开图,然后连接,再利用勾股定理即可得出的长即可得到结论.利用勾股定理求解是解题的关键.
【详解】解:如图,连接,
在圆柱的侧面展开图中,,,设,
∵点移动的最短距离为,
∴,
∵点是的中点,
∴,
∴,
∴圆柱的底面周长为:.
故选:C.
2.
【分析】本题考查了平面展开﹣最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
【详解】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
∵圆柱底面的周长为,圆柱高为,
∴,
∴,
∴,
∴这圈金属丝的周长最小为.
故答案为:.
3.
【分析】本题考查了平面展开-最短路线问题和勾股定理的应用,把立体图形展开成平面图形,依题意,从A到C缠绕了一圈半,则,,根据两点之间线段最短求出长即可解决问题.
【详解】解:如图所示,
∵无弹性的丝带从A至C,绕了1.5圈,
∴展开后,,
由勾股定理得:
故答案为:.
4.
【分析】本题主要考查了平面展开图最短路径问题,先“化曲面为平面”,把圆柱的侧面展开成矩形,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.再根据两点之间线段最短,由勾股定理可得出.
【详解】解:如图,
根据题意,, ,
∵点位于圆周顶面处,
∴,,
∴小虫爬行的最短路程.
故选:.
【题型4 圆锥中的最短路径】
1.
【分析】根据题意可得圆锥的底面周长是,即可得圆锥侧面展开图的圆心角是,展开圆锥的侧面,构造直角三角形即可得.
【详解】解:圆锥的底面周长是:,
则
,
即圆锥侧面展开图的圆心角是,
如图所示,
∴,
∵,
∴是等边三角形,
∵C是的中点,
∴,
∴,
∵在圆锥侧面展开图中,,
∴在圆锥侧面展开图中:,
∴蚂蚁在圆锥侧面上从A爬到C的最短距离是:,
故答案为:.
2.
【分析】(1)由于圆锥的底面圆周长就是圆锥的侧面展开图的弧长,利用弧长公式即可求出侧面展开图的圆心角;
(2)根据两点之间线段最短,把圆锥的侧面展开成平面图形,构造直角三角形根据勾股定理即可求得.
【详解】解(1)圆锥的底面周长,
,
解得;
故答案为.
(2)圆锥的侧面展开图如图所示,构造,根据两点之间线段最短得最短路程为:.
故答案为.
3.B
【分析】根据圆锥的底面圆周长求得半径为,根据母线长求得展开后的扇形的圆心角为,进而即可求解.
【详解】解:∵这个圆锥的底面圆周长为 ,
∴
解得:
∵
解得:
∴侧面展开图的圆心角为
如图所示,即为所求,过点作,
∵,,则
∵,则
∴,,
故选:B.
4.C
【分析】求出圆锥底面圆的周长,则以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,根据弧长公式求出展开后扇形的圆心角,求出展开后∠BAC=90°,连接BP,根据勾股定理求出BP即可.
【详解】圆锥底面是以BC为直径的圆,圆的周长是 6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则
解得:n=180,
即展开后
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:
故选C.
【题型5 台阶中的最短路径】
1.C
【分析】本题考查平面展开—最短路径问题,勾股定理.根据题意画出台阶的侧面展开图,再根据勾股定理求出的长即可得出结论.
【详解】解:如图所示,
,
.
故选C.
2.C
【分析】本题考查的是平面展开-最短路线问题,根据题意画出台阶的平面展开图,再用勾股定理根据两点之间线段最短进行解答.
【详解】解:如图所示,
∵它的每一级的长宽高分别为,
∴
即:蚂蚁沿着台阶面爬行到点N的最短路程是,
故选:C.
3.C
【分析】本题主要考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.将台阶展开为矩形,然后利用勾股定理计算的值,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】解:如下图,将台阶展开为矩形,线段恰好是直角三角形的斜边,
则,,
在中,,
所以蚂蚁所走的最短路线长度为5.
故选:C.
4.
【分析】展开成平面图形,根据勾股定理,即可求解,本题考查了勾股定理的应用,解题的关键是:利用两点之间线段最短.
【详解】解:将台阶展开成平面图形:
在中,,,
,
其爬行的最短长度,
故答案为:.
【题型6 由垂线段最短求最短路径】
1.
【分析】连接,BP,根据等腰三角形的性质可得CD垂直平分AB,从而得到AP=BP,进而得到就是的最小值,再由勾股定理求出BE,即可求解.
【详解】解:如图,连接,BP,
∵,点是的中点,
∴CD垂直平分AB,
∴AP=BP,
∴AP+PE=BP+PE≥BE,
∴就是的最小值,
∵中,,点,分别是,的中点,
∴,
∴,
∴的最小值是.
故答案为:.
2.解:过点C作,垂足为D点,
则这条水泥路的最短距离为的长度,
,
在中,,,,
则,即:,
∴为直角三角形,
∴,
这条水泥路的最短距离为.
3.D
【分析】本题主要考查了勾股定理,正确理解勾股定理的含义是解题关键.过点C作,设千米,则千米,由勾股定理可得,列出方程求解,再用勾股定理求出即可得出答案.
【详解】如图,过点C作,
设千米,则千米,
,
,
,
,
千米,
(千米),
费用最低为万元.
故选:D
4.
【分析】本题主要考查的是轴对称的性质、勾股定理的应用、垂线段最短等知识,解题的关键是学利用对称,解决最短问题.
如图所示:在上取点,使,过点C作,垂足为H.因为,推出当C、E、共线,且点与H重合时,的值最小.
【详解】解:如图所示:在上取点,使,
∵,
∴,
∴.
在中,
.
过点C作,垂足为H.
,
,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为的长,
的值最小为,
故答案为:.
【题型7 由将军饮马求最短路径】
1.17
【分析】如图(见详解),将小河看成直线MN,由题意先作A关于MN的对称点,连接A`B,构建直角三角形,则A`B就是最短路线;在Rt△A`DB中,∠A`DB=90°,BD=8km,A`D=AD+A`A,利用勾股定理即可求出A`B.
【详解】如图,做出点A关于小河MN的对称点A`,连接A`B交MN于点P,则A`B就是牧童要完成这件事情所走的最短路程长度.
在Rt△A`DB中,由勾股定理求得.
则他要完成这件事情所走的最短路程是17km.
2.解:如图,作点关于的对称点,连接交于,点即为水厂的位置.
分过点作交的延长线于点,过点作于点,
则,,.
∴.
在中,,
∴,
∴.
在中,,
由勾股定理得.
∴(元).
故铺设水管的总费用为20000元.
3.
【分析】表示直线与直线之间的距离,是定值,只要满足的值最小即可.过作直线的垂线,并在此垂线上取点,使得,连接,则与直线的交点即为,过作于点.则为所求,利用勾股定理可求得其值.
【详解】解:过作直线的垂线,并在此垂线上取点,使得,连接,与直线交于点,过作直线的垂线,交直线于点,连接,过点作,交射线于点,如图.
,,
.
又,
四边形是平行四边形,
.
由于要最小,且固定为4,所以最小.
由两点之间线段最短,可知的最小值为.
,,
,
,
所以的最小值为.
故答案为:.
【题型8 不规则图形中求最短路径】
1.C
【分析】本题考查平面展开—最短路径问题及勾股定理的应用,可将教室的墙面与地面展开,连接,根据两点之间线段最短,利用勾股定理求解即可.正确利用立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决是解题的关键.
【详解】解:如图,过作于,连接,
此时的长为这只蚂蚁从点爬到点的最短行程,
∵米,米,点到的距离是米,
∴米,
∴(米),
∴(米),
∴(米),
∴这只蚂蚁的最短行程应该是米.
故选:C.
2.13
【分析】将木块展开看作平面后,由两点之间线段最短知蚂蚁的最短距离为线段AC,由勾股定理计算即可.
【详解】将长方形纸片与木块展开后如图所示
由两点之间线段最短可知蚂蚁的最短距离为线段AC
此时AB长度为11-1+2=12
由勾股定理有
即
故答案为:13.
3.20
【分析】本题主要考查了勾股定理的应用—最短路径问题.通过将U型池的侧面展开成矩形,“化曲面为平面”,用勾股定理求最短路径是解题的关键.将半圆面展开,连接,则是最短路径,根据,计算求解即可.
【详解】解:将半圆面展开如图:连接,则是最短路径,
∴,,
由勾股定理得,.
∴滑行的最短距离约为,
故答案为:20.
4.A
【分析】本题考查勾股定理的应用.根据两点之间线段最短,将图②展开,利用勾股定理进行求解即可.
【详解】解:如图,正方体上表面的对角线为,将图②展开,连接交于点,线段的长度即为蚂蚁爬行的最短路程,
由题意可知:为等边三角形,为等腰直角三角形,
,,,
,
,
,
正方体的棱长为4,
,,
在中,,
在中,,
.
故选:A.
