3.4.2.2与相似三角形的周长、面积有关的性质 课件(共19张PPT)
文档属性
| 名称 | 3.4.2.2与相似三角形的周长、面积有关的性质 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 17:05:40 | ||
图片预览




文档简介
(共19张PPT)
第三章 图形的相似 3.4.2
相似三角形的性质
3.4.2.2 与相似三角形的周长、面积有关的性质
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
情境导入
如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10平方米,CE长为4m,BE长为6m.
根据所测得的数据,请你计算出整个花坛△ABC的面积.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究新知
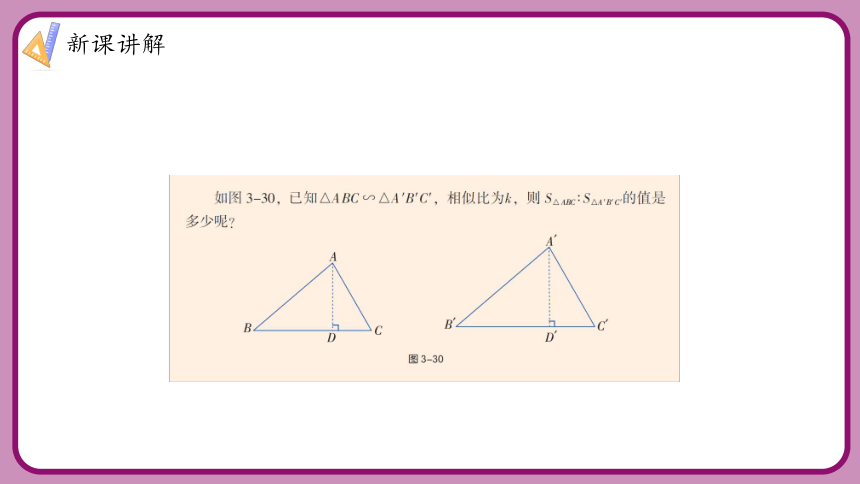
新课讲解
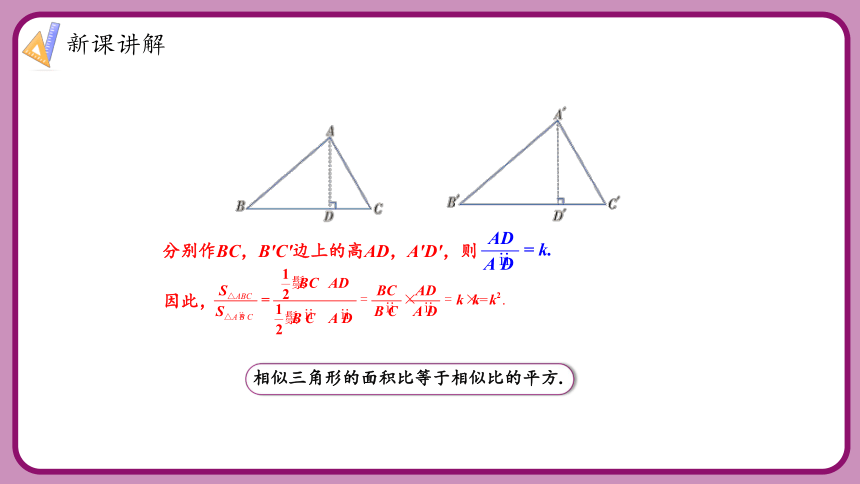
分别作BC,B′C′边上的高AD,A′D′,则
因此,
相似三角形的面积比等于相似比的平方.
新课讲解
情境导入
如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10平方米,CE长为4m,BE长为6m.
根据所测得的数据,请你计算出整个花坛△ABC的面积.
S△CDE=10m2
CE=4m
BE=6m
求S△ABC
新课讲解
相似三角形的面积比等于相似比的平方.
S△CDE=10m2
CE=4m
BE=6m
求S△ABC
∴S△ABC=62.5m2.
∵S△CDE=10m2.
∵DE∥AB,
∴△CDE∽△CAB.
新课讲解
例11
如图,在△ABC中,EF∥BC, ,S四边形BCFE=8,求S△ABC.
解:∵EF∥BC,∴△AEF∽△ABC.
∵S四边形BCFE=8,
∴S△AEF=1.
∴S△ABC=9.
新课讲解
例12
已知△ABC与△A′B′C′的相似比为 ,且S△ABC+S△A′B′C′=91,
求△A′B′C′的面积.
解:∵ △ABC与△A′B′C′的相似比为 ,
又 S△ABC+ S△A′B′C′ =91,
∴S△A′B′C′ =63.
新课讲解
课堂练习
1.证明:相似三角形的周长比等于相似比.
A
B
C
A′
B′
C′
课堂练习
A
B
C
A′
B′
C′
证明:∵△A′B′C′∽△ABC,其相似比为k,
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′).
∵C△A′B′C′= A′B′+A′C′+B′C′,
相似三角形的周长比等于相似比.
课堂练习
2.已知△ABC∽△ A′B′C′,它们的周长分别为60cm
和72cm,且AB=15cm,B′C′=24cm,求BC,AC, A′B′, A′C′的长.
A
B
C
A′
B′
C′
解:∵△ABC∽△A′B′C′ ,
∵ AB=15cm,B′C′=24cm,
∴ A′B′=18cm,BC=20cm.
∵C△ABC=60, C△A′B′C′ =72,
∴ AC=25cm,A′C′=30cm.
课堂练习
3.有一个直角三角形的边长分别为3,4,5,另一个与它
相似的直角三角形的最小边长为7,则另一个直角三角形的周长和面积分别是多少?
A
B
C
A′
B′
C′
解:∵Rt△A′B′C′∽Rt△ABC,
∵C△ABC=12,∴C△A′B′C′ =28.
∵S△ABC=6,
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第三章 图形的相似 3.4.2
相似三角形的性质
3.4.2.2 与相似三角形的周长、面积有关的性质
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
情境导入
如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10平方米,CE长为4m,BE长为6m.
根据所测得的数据,请你计算出整个花坛△ABC的面积.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究新知
新课讲解
分别作BC,B′C′边上的高AD,A′D′,则
因此,
相似三角形的面积比等于相似比的平方.
新课讲解
情境导入
如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10平方米,CE长为4m,BE长为6m.
根据所测得的数据,请你计算出整个花坛△ABC的面积.
S△CDE=10m2
CE=4m
BE=6m
求S△ABC
新课讲解
相似三角形的面积比等于相似比的平方.
S△CDE=10m2
CE=4m
BE=6m
求S△ABC
∴S△ABC=62.5m2.
∵S△CDE=10m2.
∵DE∥AB,
∴△CDE∽△CAB.
新课讲解
例11
如图,在△ABC中,EF∥BC, ,S四边形BCFE=8,求S△ABC.
解:∵EF∥BC,∴△AEF∽△ABC.
∵S四边形BCFE=8,
∴S△AEF=1.
∴S△ABC=9.
新课讲解
例12
已知△ABC与△A′B′C′的相似比为 ,且S△ABC+S△A′B′C′=91,
求△A′B′C′的面积.
解:∵ △ABC与△A′B′C′的相似比为 ,
又 S△ABC+ S△A′B′C′ =91,
∴S△A′B′C′ =63.
新课讲解
课堂练习
1.证明:相似三角形的周长比等于相似比.
A
B
C
A′
B′
C′
课堂练习
A
B
C
A′
B′
C′
证明:∵△A′B′C′∽△ABC,其相似比为k,
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′).
∵C△A′B′C′= A′B′+A′C′+B′C′,
相似三角形的周长比等于相似比.
课堂练习
2.已知△ABC∽△ A′B′C′,它们的周长分别为60cm
和72cm,且AB=15cm,B′C′=24cm,求BC,AC, A′B′, A′C′的长.
A
B
C
A′
B′
C′
解:∵△ABC∽△A′B′C′ ,
∵ AB=15cm,B′C′=24cm,
∴ A′B′=18cm,BC=20cm.
∵C△ABC=60, C△A′B′C′ =72,
∴ AC=25cm,A′C′=30cm.
课堂练习
3.有一个直角三角形的边长分别为3,4,5,另一个与它
相似的直角三角形的最小边长为7,则另一个直角三角形的周长和面积分别是多少?
A
B
C
A′
B′
C′
解:∵Rt△A′B′C′∽Rt△ABC,
∵C△ABC=12,∴C△A′B′C′ =28.
∵S△ABC=6,
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
