2025年中考数学二轮复习专题3 与中点相关的辅助线添加 课件(共23张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习专题3 与中点相关的辅助线添加 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 473.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 07:22:17 | ||
图片预览





文档简介
(共23张PPT)
专题三 与中点相关的辅助线添加
类型一 构造三角形的中线
当已知条件中出现“中点”,可结合图形特点构造三角形的中
线,与“中线将三角形面积两等分”或“等腰三角形三线合一”或
“直角三角形斜边上的中线等于斜边的一半”相联系.
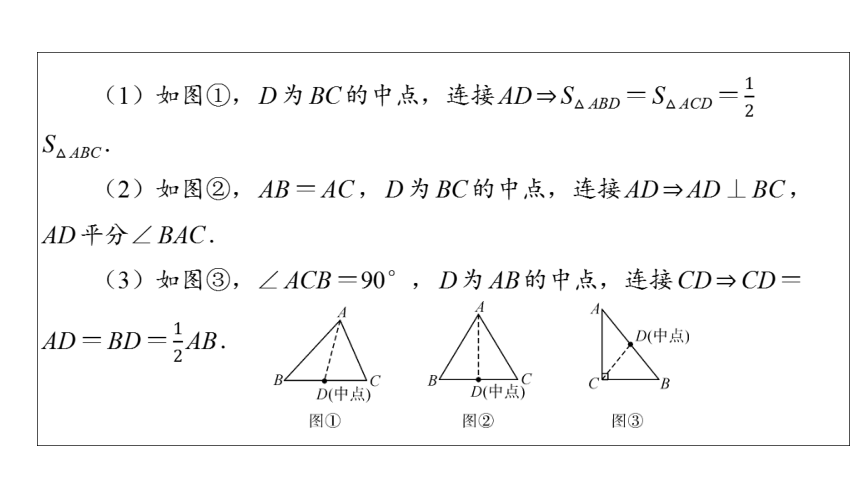
(1)如图①,D为BC的中点,连接AD S△ABD=S△ACD=
S△ABC.
(2)如图②,AB=AC,D为BC的中点,连接AD AD⊥BC,
AD平分∠BAC.
(3)如图③,∠ACB=90°,D为AB的中点,连接CD CD=
AD=BD= AB.
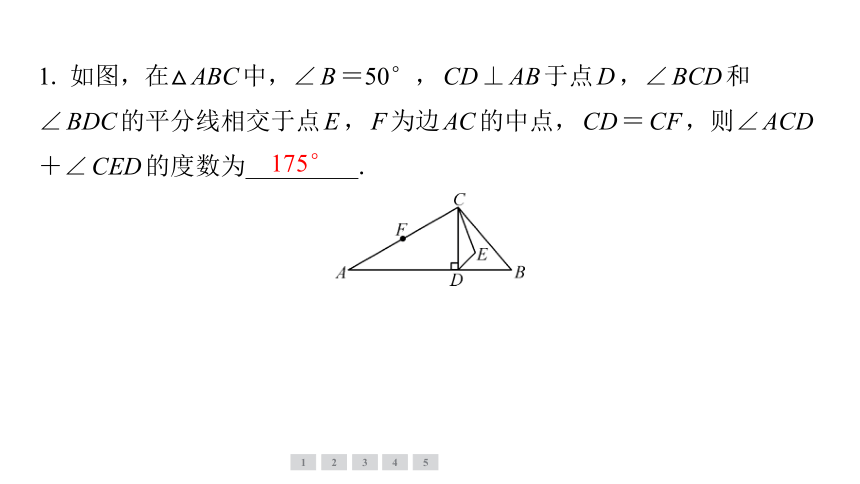
1. 如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和
∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD
+∠CED的度数为 .
175°
1
2
3
4
5
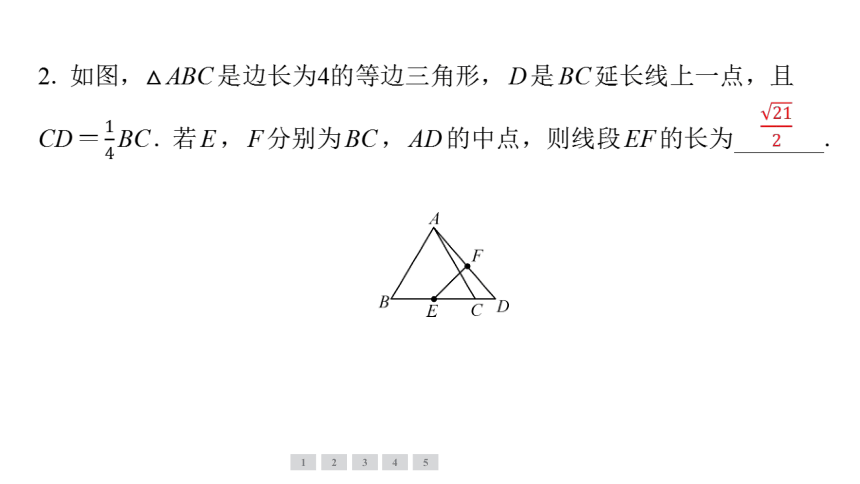
2. 如图,△ABC是边长为4的等边三角形,D是BC延长线上一点,且
CD= BC. 若E,F分别为BC,AD的中点,则线段EF的长为 .
1
2
3
4
5
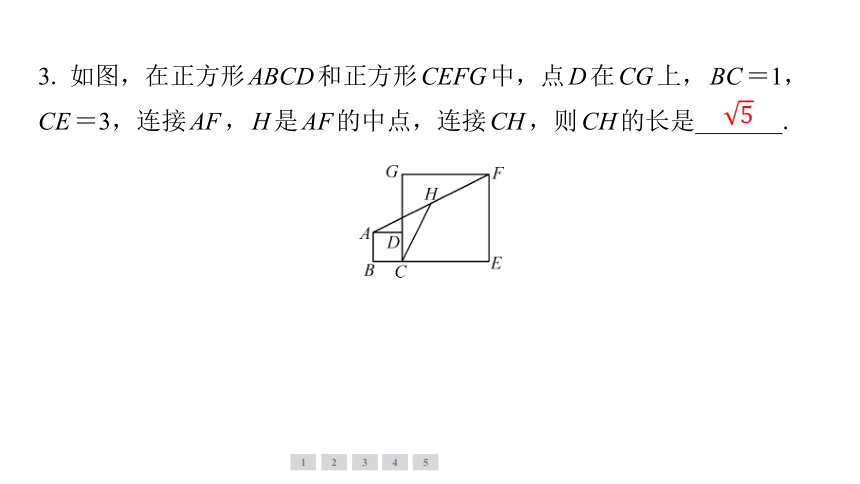
3. 如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,
CE=3,连接AF,H是AF的中点,连接CH,则CH的长是 .
1
2
3
4
5
4. 如图,在△ABC中,AD⊥BC于点D,CE是AB边上的中线,
DG⊥CE于点G,CD=AE. 若AB=10,DG=3,则CE的长
为 .
8
1
2
3
4
5
5. 如图,在平面直角坐标系中,已知A(1,3),B(4,2),若经过
点A的直线l将△AOB的面积两等分,则直线l的解析式为 .
y=-2x+ 5
1
2
3
4
5
类型二 构造三角形的中位线
当已知条件中出现“中点”,可结合图形特点构造三角形的中
位线.
1
2
3
4
5
(1)如图①,“连接两中点构造中位线”→D,E分别为AB,
AC的中点,连接DE,则DE为△ABC的中位线→DE∥BC且DE=
BC,△ADE∽△ABC.
(2)如图②,“过一中点作平行线构造中位线”→D为AB的中
点,作DE∥BC,则DE为△ABC的中位线→DE= BC,
△ADE∽△ABC.
(3)如图③,“作平行线补形构造中位线”→D为AB中点,作
AF∥DE,则DE为△ABF的中位线→DE= AF,△BDE∽△BAF.
1
2
3
4
5
1. 如图,在Rt△ABC中,∠A=90°,AC=6,BC=10,D是BC边的
中点,E在AB边上,且∠DEB=45°,则四边形ACDE的周长
为 .
3 +12
1
2
3
4
2. 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AB的中点,
F是DC的中点,连接EF交AD于点P. 若△ABC的面积是24,PD=
1.5,则BC的长为 .
8
1
2
3
4
3. 如图,在△ABC中,AC=2 ,∠ACB=120°,D是边AB的中
点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为 .
1
2
3
4
4. 如图,AD是△ABC的中线,E为AD上一点, = ,CE的延长线
交AB于点F,则 = .
1
2
3
4
类型三 倍长中线和类中线
当已知条件中出现“中线或中点”时,可结合图形特点“倍长中
线”构造全等三角形,达到线段、角的等量转化.
1
2
3
4
(1)如图①,“倍长中线”→D为AC中点,延长BD至点E,使
得BD=ED,则△ABD≌△CED(SAS).
(2)如图②,“倍长类中线”→D为BC中点,延长ED至点F,
使得ED=FD,则△EBD≌△FCD(SAS).
1
2
3
4
1. 如图,在△ABC中,D为BC边的中点.若AB=4,AD=3,AC=
x,则x的取值范围是 .
2<x<10
1
2
3
4
5
6
2. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,CD为斜
边BC上的中线,在AD上取一点F,连接AF并延长,交BC于点E. 若
CE=EF,则AF的长为 .
6
1
2
3
4
5
6
3. 如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,
DC⊥BC,则△ABC的面积为 .
8
1
2
3
4
5
6
4. 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,
BC边上的点,且GE⊥EF. 若AG=2,BF=3,则正方形ABCD的边长
为 .
2
1
2
3
4
5
6
5. 如图,在△ABC中,∠C=90°,点D,E分别在AC,BC边上,
且AD=2,BE=1,连接DE,M,N分别为AB,DE的中点,连接
MN,则MN的长为 .
1
2
3
4
5
6
6. 如图,在菱形ABCD中,E是边AB的中点,F是边AD上一点,连接
CE,EF. 若BC=6,EF=2AF=4,则CE的长为 .
6
1
2
3
4
5
6
谢谢观看
专题三 与中点相关的辅助线添加
类型一 构造三角形的中线
当已知条件中出现“中点”,可结合图形特点构造三角形的中
线,与“中线将三角形面积两等分”或“等腰三角形三线合一”或
“直角三角形斜边上的中线等于斜边的一半”相联系.
(1)如图①,D为BC的中点,连接AD S△ABD=S△ACD=
S△ABC.
(2)如图②,AB=AC,D为BC的中点,连接AD AD⊥BC,
AD平分∠BAC.
(3)如图③,∠ACB=90°,D为AB的中点,连接CD CD=
AD=BD= AB.
1. 如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和
∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD
+∠CED的度数为 .
175°
1
2
3
4
5
2. 如图,△ABC是边长为4的等边三角形,D是BC延长线上一点,且
CD= BC. 若E,F分别为BC,AD的中点,则线段EF的长为 .
1
2
3
4
5
3. 如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,
CE=3,连接AF,H是AF的中点,连接CH,则CH的长是 .
1
2
3
4
5
4. 如图,在△ABC中,AD⊥BC于点D,CE是AB边上的中线,
DG⊥CE于点G,CD=AE. 若AB=10,DG=3,则CE的长
为 .
8
1
2
3
4
5
5. 如图,在平面直角坐标系中,已知A(1,3),B(4,2),若经过
点A的直线l将△AOB的面积两等分,则直线l的解析式为 .
y=-2x+ 5
1
2
3
4
5
类型二 构造三角形的中位线
当已知条件中出现“中点”,可结合图形特点构造三角形的中
位线.
1
2
3
4
5
(1)如图①,“连接两中点构造中位线”→D,E分别为AB,
AC的中点,连接DE,则DE为△ABC的中位线→DE∥BC且DE=
BC,△ADE∽△ABC.
(2)如图②,“过一中点作平行线构造中位线”→D为AB的中
点,作DE∥BC,则DE为△ABC的中位线→DE= BC,
△ADE∽△ABC.
(3)如图③,“作平行线补形构造中位线”→D为AB中点,作
AF∥DE,则DE为△ABF的中位线→DE= AF,△BDE∽△BAF.
1
2
3
4
5
1. 如图,在Rt△ABC中,∠A=90°,AC=6,BC=10,D是BC边的
中点,E在AB边上,且∠DEB=45°,则四边形ACDE的周长
为 .
3 +12
1
2
3
4
2. 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AB的中点,
F是DC的中点,连接EF交AD于点P. 若△ABC的面积是24,PD=
1.5,则BC的长为 .
8
1
2
3
4
3. 如图,在△ABC中,AC=2 ,∠ACB=120°,D是边AB的中
点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为 .
1
2
3
4
4. 如图,AD是△ABC的中线,E为AD上一点, = ,CE的延长线
交AB于点F,则 = .
1
2
3
4
类型三 倍长中线和类中线
当已知条件中出现“中线或中点”时,可结合图形特点“倍长中
线”构造全等三角形,达到线段、角的等量转化.
1
2
3
4
(1)如图①,“倍长中线”→D为AC中点,延长BD至点E,使
得BD=ED,则△ABD≌△CED(SAS).
(2)如图②,“倍长类中线”→D为BC中点,延长ED至点F,
使得ED=FD,则△EBD≌△FCD(SAS).
1
2
3
4
1. 如图,在△ABC中,D为BC边的中点.若AB=4,AD=3,AC=
x,则x的取值范围是 .
2<x<10
1
2
3
4
5
6
2. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,CD为斜
边BC上的中线,在AD上取一点F,连接AF并延长,交BC于点E. 若
CE=EF,则AF的长为 .
6
1
2
3
4
5
6
3. 如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,
DC⊥BC,则△ABC的面积为 .
8
1
2
3
4
5
6
4. 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,
BC边上的点,且GE⊥EF. 若AG=2,BF=3,则正方形ABCD的边长
为 .
2
1
2
3
4
5
6
5. 如图,在△ABC中,∠C=90°,点D,E分别在AC,BC边上,
且AD=2,BE=1,连接DE,M,N分别为AB,DE的中点,连接
MN,则MN的长为 .
1
2
3
4
5
6
6. 如图,在菱形ABCD中,E是边AB的中点,F是边AD上一点,连接
CE,EF. 若BC=6,EF=2AF=4,则CE的长为 .
6
1
2
3
4
5
6
谢谢观看
同课章节目录
