生活中的轴对称单元测试卷(附答案)

简单的轴对称图形专题训练
一．选择题（共13小题）
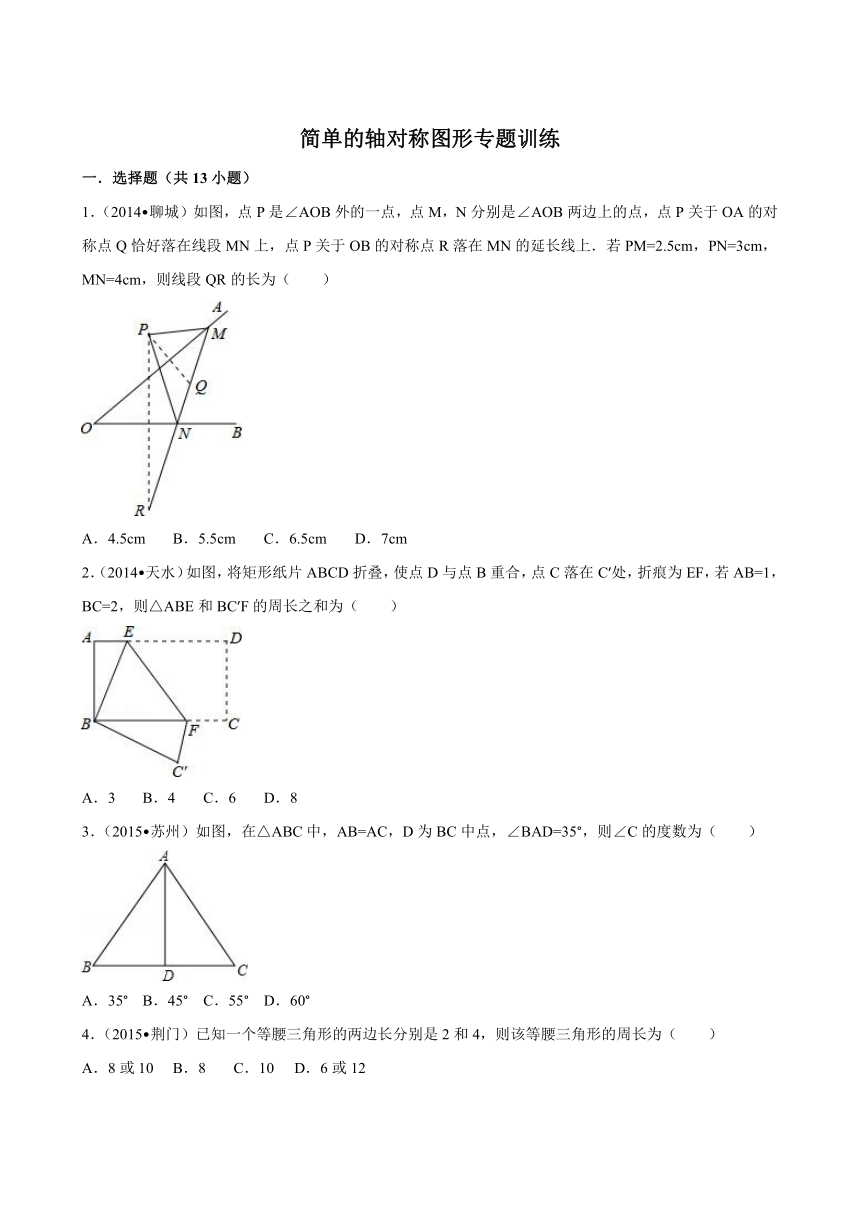
1．（2014 聊城）如图，点P是∠AO ( http: / / www.21cnjy.com )B外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=2.5cm，PN=3cm，MN=4cm，则线段QR的长为（　　）
( http: / / www.21cnjy.com )
A．4.5cm B．5.5cm C．6.5cm D．7cm
2．（2014 天水）如图，将矩形纸片AB ( http: / / www.21cnjy.com )CD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和BC′F的周长之和为（　　）
( http: / / www.21cnjy.com )
A．3 B．4 C．6 D．8
3．（2015 苏州）如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为（　　）
( http: / / www.21cnjy.com )
A．35° B．45° C．55° D．60°
4．（2015 荆门）已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（　　）
A．8或10 B．8 C．10 D．6或12
5．（2015 内江）如图，在△ABC中， ( http: / / www.21cnjy.com )AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（　　）
( http: / / www.21cnjy.com )
A．40° B．45° C．60° D．70°
6．（2015 丹东）如图 ( http: / / www.21cnjy.com )，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）
( http: / / www.21cnjy.com )
A．15° B．17.5° C．20° D．22.5°
7．（2015 茂名）如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（　　）
( http: / / www.21cnjy.com )
A．6 B．5 C．4 D．3
8．（2011 衢州）如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（　　）
( http: / / www.21cnjy.com )
A．1 B．2 C．3 D．4
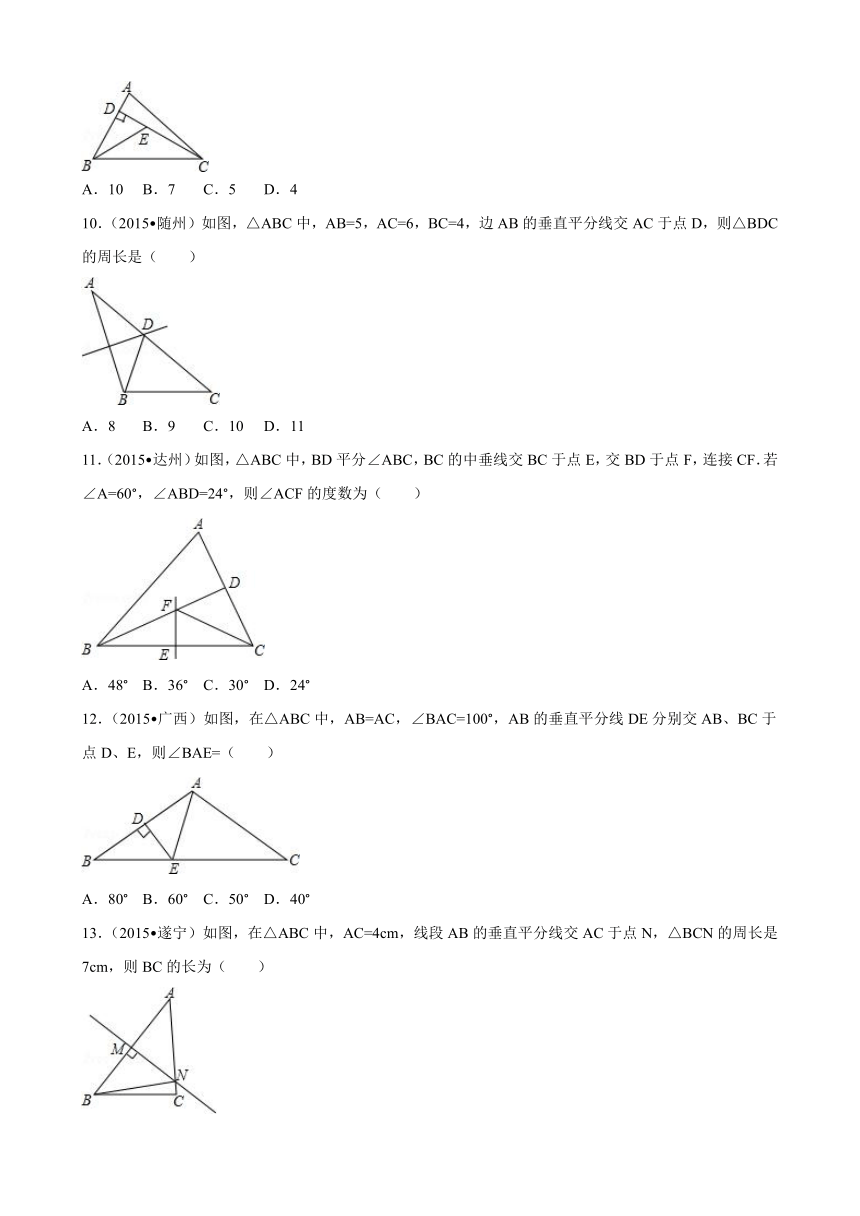
9．（2015 湖州）如图，已知在△A ( http: / / www.21cnjy.com )BC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（　　）
( http: / / www.21cnjy.com )
A．10 B．7 C．5 D．4
10．（2015 随州）如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（　　）
( http: / / www.21cnjy.com )
A．8 B．9 C．10 D．11
11．（2015 达州）如图，△A ( http: / / www.21cnjy.com )BC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（　　）
( http: / / www.21cnjy.com )
A．48° B．36° C．30° D．24°
12．（2015 广西）如图，在△ ( http: / / www.21cnjy.com )ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（　　）
( http: / / www.21cnjy.com )
A．80° B．60° C．50° D．40°
13．（2015 遂宁）如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（　　）
( http: / / www.21cnjy.com )
A．1cm B．2cm C．3cm D．4cm
　
二．填空题（共7小题）
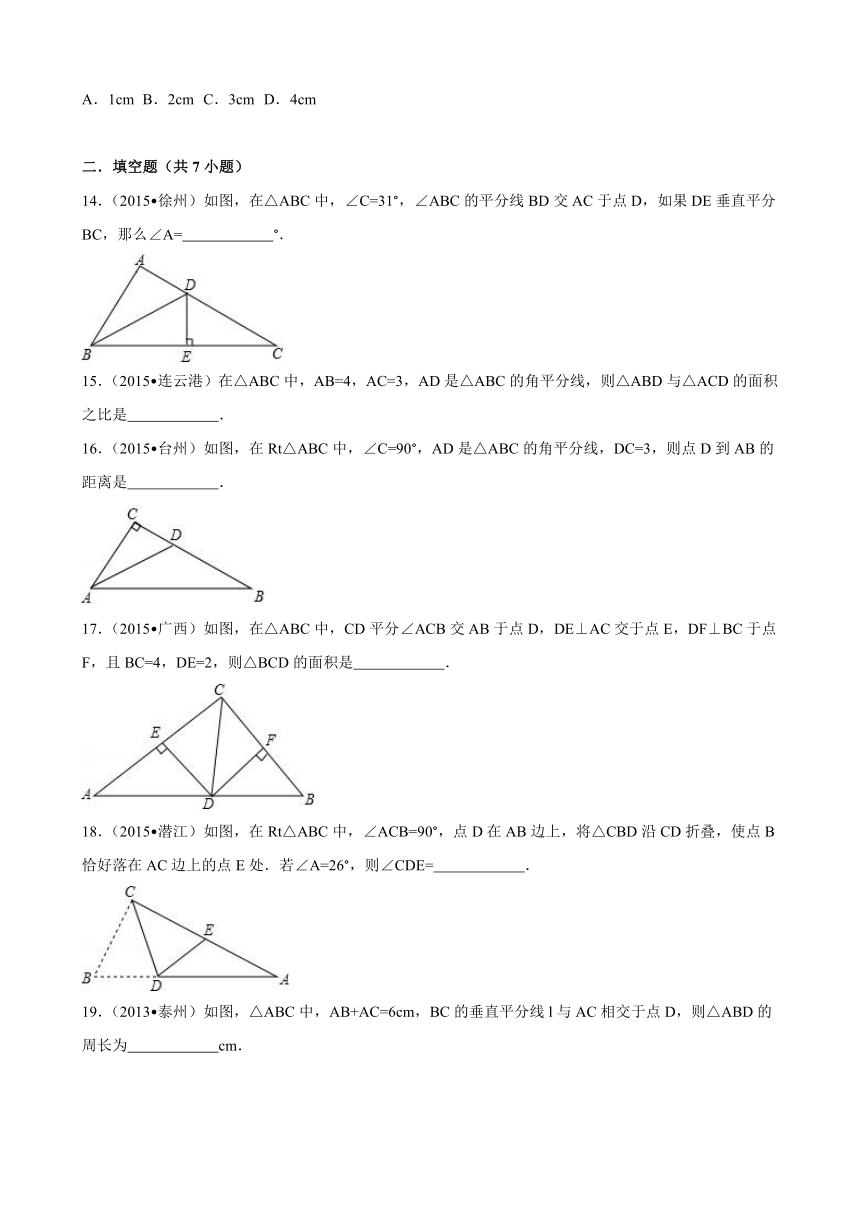
14．（2015 徐州）如图，在△ABC中， ( http: / / www.21cnjy.com )∠C=31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A=　　　　　　°．
( http: / / www.21cnjy.com )
15．（2015 连云港）在△ABC中，AB=4，AC=3，AD是△ABC的角平分线，则△ABD与△ACD的面积之比是　　　　　　．
16．（2015 台州）如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DC=3，则点D到AB的距离是　　　　　　．
( http: / / www.21cnjy.com )
17．（2015 广西）如 ( http: / / www.21cnjy.com )图，在△ABC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC=4，DE=2，则△BCD的面积是　　　　　　．
( http: / / www.21cnjy.com )
18．（2015 潜江） ( http: / / www.21cnjy.com )如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处．若∠A=26°，则∠CDE=　　　　　　．
( http: / / www.21cnjy.com )
19．（2013 泰州）如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为　　　　　　cm．
( http: / / www.21cnjy.com )
20．（2015 南通）如图，△ABC中，D是BC上一点，AC=AD=DB，∠BAC=102°，则∠ADC=　　　　　　度．
( http: / / www.21cnjy.com )
　
三．解答题（共8小题）
21．（2015 北京）如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．
( http: / / www.21cnjy.com )
22．（2015 宿迁）如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．
( http: / / www.21cnjy.com )
23．（2015 台湾）如图，四边形A ( http: / / www.21cnjy.com )BCD中，AC为∠BAD的角平分线，AB=AD，E、F两点分别在AB、AD上，且AE=DF．请完整说明为何四边形AECF的面积为四边形ABCD的一半．
( http: / / www.21cnjy.com )
24．（2013 淄博）如图，AD∥BC，BD平分∠ABC．求证：AB=AD．
( http: / / www.21cnjy.com )
25．（2016 历下区一模）如图，在△ABC中，AB=AC，点D是BC边上的中点，DE、DF分别垂直AB、AC于点E和F．
求证：DE=DF．
( http: / / www.21cnjy.com )
26．（2016 门头沟区一模）如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE=CD．
求证：BD=DE．
( http: / / www.21cnjy.com )
27．（2016 历下区一模）如图，在△ABC中，∠ACB=90゜，BE平分∠ABC，交AC于E，DE垂直平分AB于D，
求证：BE+DE=AC．
( http: / / www.21cnjy.com )
28．（2015秋 九台市期末）如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，求△ABC的周长．
( http: / / www.21cnjy.com )
　
参考答案
一．选择题（共13小题）
1． A．　2． C．　3． C．　4． C．　5． A．　6． A．　7． A．　8． B．
9． C．　10． C．　11． A．　12． D．　13． C．　
二．填空题（共7小题）
14． 87．　15． 4：3．　16． 3．　17． 4．　18． 71°．　19． 6．　20． 52．　
三．解答题（共8小题）
21．证明：∵AB=AC，AD是BC边上的中线，BE⊥AC，
∴∠CBE+∠C=∠CAD+∠C=90°，∠CAD=∠BAD，
∴∠CBE=∠BAD．
　
22．证明：∵AB=AC=AD，
∴∠C=∠ABC，∠D=∠ABD，
∴∠ABC=∠CBD+∠D，
∵AD∥BC，
∴∠CBD=∠D，
∴∠ABC=∠D+∠D=2∠D，
又∵∠C=∠ABC，
∴∠C=2∠D．
　
23．解：分别作CG⊥AB与G，CH⊥AD与H，
∵AC为∠BAD的角平分线，
∴CG=CH，
∵AB=AD，
∴△ABC面积=△ACD面积，
又∵AE=DF，
∴△AEC面积=△CDF面积，
∴△BCE面积=△ABC面积﹣△AEC面积，
△BCE面积=△ACD面积﹣△CDF面积，
∴△BCE面积=△ACF面积，
∵四边形AECF面积=△AEC面积+△ACF面积，
四边形AECF面积=△AEC面积+△BCE面积，
∴四边形AECF面积=△ABC面积，
又∵四边形ABCD面积=△ABC面积+△ACD面积，
又∵四边形ABCD面积=2△ABC面积，
∴四边形AECF面积为四边形ABCD面积的一半．
( http: / / www.21cnjy.com )
　
24．证明：
证法一：连接AD．
∵AB=AC，点D是BC边上的中点
∴AD平分∠BAC（三线合一性质），
∵DE、DF分别垂直AB、AC于点E和F．
∴DE=DF（角平分线上的点到角两边的距离相等）．
证法二：在△ABC中，
∵AB=AC
∴∠B=∠C（等边对等角） …（1分）
∵点D是BC边上的中点
∴BD=DC …（2分）
∵DE、DF分别垂直AB、AC于点E和F
∴∠BED=∠CFD=90°…（3分）
在△BED和△CFD中
∵，
∴△BED≌△CFD（AAS），
∴DE=DF（全等三角形的对应边相等）．
( http: / / www.21cnjy.com )
　
26．证明：∵△ABC是等边三角形，BD是中线，
∴∠ABC=∠ACB=60°．
∠DBC=30°（等腰三角形三线合一）．
又∵CE=CD，
∴∠CDE=∠CED．
又∵∠BCD=∠CDE+∠CED，
∴∠CDE=∠CED=∠BCD=30°．
∴∠DBC=∠DEC．
∴DB=DE（等角对等边）．
　
27．证明：∵∠ACB=90°，
∴AC⊥BC，
∵ED⊥AB，BE平分∠ABC，
∴CE=DE，
∵DE垂直平分AB，
∴AE=BE，
∵AC=AE+CE，
∴BE+DE=AC．
　
28．解：∵DE是AC的垂直平分线，AE=3cm，
∴AD=CD，AC=2AE=2×3=6cm，
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm，
∴△ABC的周长=AB+BC+AC=13+6=19cm．