浙教版七下期中拓展培优卷(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
七下期中拓展培优卷
一、选择题
1.(2023七下·北仑期中)如图,当光线从空气进入水中时,会发生折射,满足入射角与折射角的度数比为,如图,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面夹角分别为,,在水中两条折射光线的夹角为,则,,三者之间的数量关系为( )
A. B.
C. D.
2.(2024七下·杭州期中)已知,是常数,若化简的结果不含的二次项,则的值为( )
A. B. C. D.
3.(2025七下·嘉兴月考)小宸的综合实践活动报告部分信息如下图,则用十六进制表示的结果是( )
综合实践活动:寻找数和计算工具的发展足迹
十六进制:缝十六进一,采用数字和字母共16个计数符号.
十六进制的符号和十进制的数的对应关系:
16进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
10进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例:,
A.182 B.DE C. D.
4.(2024七下·温州期中)①过一点有且只有一条直线与已知直线平行;
②无论取何实数,多项式总能分解成两个一次因式积的形式;
③若,则可以取的值有2个;
④关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是.其中正确的有( )
A.①③ B.①④ C.②④ D.③④
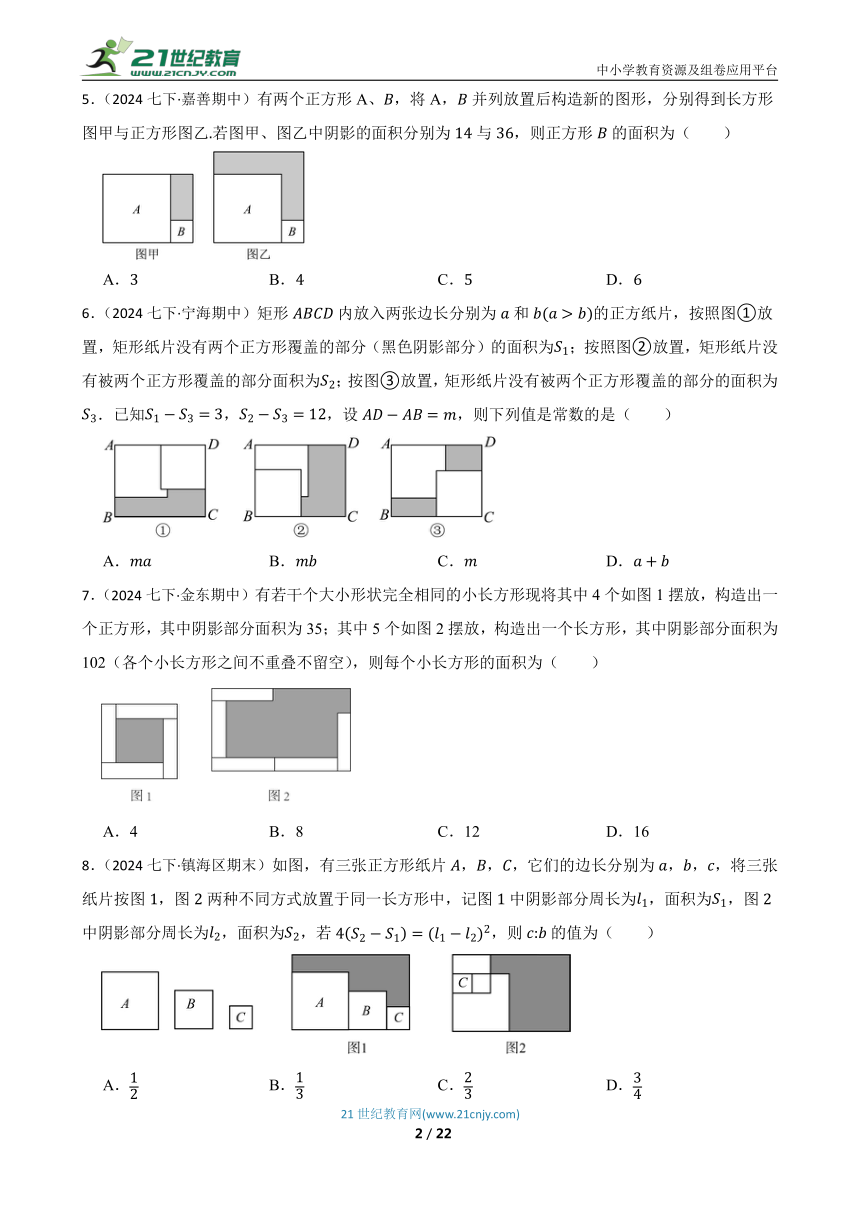
5.(2024七下·嘉善期中)有两个正方形A、,将A,并列放置后构造新的图形,分别得到长方形图甲与正方形图乙若图甲、图乙中阴影的面积分别为与,则正方形的面积为( )
A. B. C. D.
6.(2024七下·宁海期中)矩形内放入两张边长分别为和的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为.已知,,设,则下列值是常数的是( )
A. B. C. D.
7.(2024七下·金东期中)有若干个大小形状完全相同的小长方形现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为35;其中5个如图2摆放,构造出一个长方形,其中阴影部分面积为102(各个小长方形之间不重叠不留空),则每个小长方形的面积为( )
A.4 B.8 C.12 D.16
8.(2024七下·镇海区期末)如图,有三张正方形纸片,,,它们的边长分别为,,,将三张纸片按图,图两种不同方式放置于同一长方形中,记图中阴影部分周长为,面积为,图中阴影部分周长为,面积为,若,则的值为( )
A. B. C. D.
二、填空题
9.(2024七下·杭州期中)已知关于,的方程组,
(1),互为相反数时, ;
(2) ;
(3)若,满足,则 .
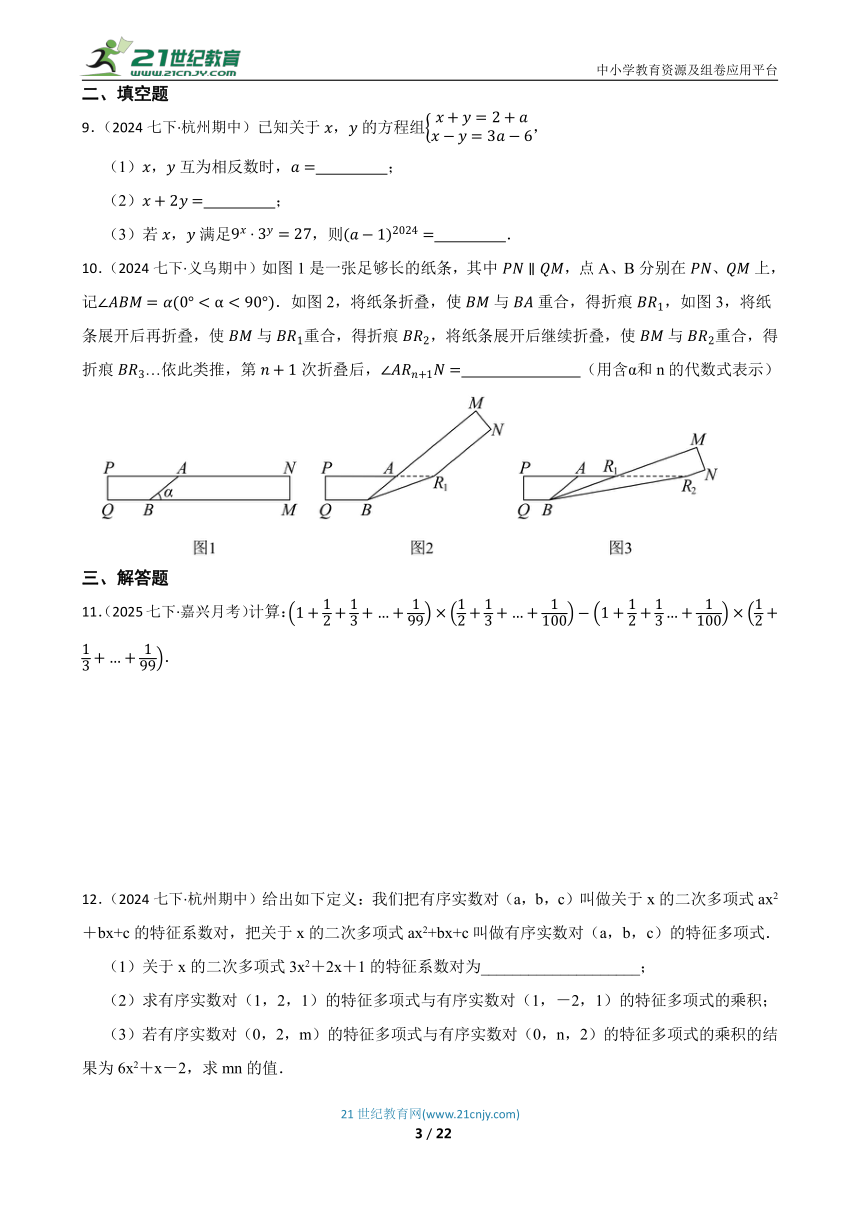
10.(2024七下·义乌期中)如图1是一张足够长的纸条,其中,点A、B分别在、上,记.如图2,将纸条折叠,使与重合,得折痕,如图3,将纸条展开后再折叠,使与重合,得折痕,将纸条展开后继续折叠,使与重合,得折痕…依此类推,第次折叠后, (用含α和n的代数式表示)
三、解答题
11.(2025七下·嘉兴月考)计算:.
12.(2024七下·杭州期中)给出如下定义:我们把有序实数对(a,b,c)叫做关于x的二次多项式ax2+bx+c的特征系数对,把关于x的二次多项式ax2+bx+c叫做有序实数对(a,b,c)的特征多项式.
(1)关于x的二次多项式3x2+2x+1的特征系数对为____________________;
(2)求有序实数对(1,2,1)的特征多项式与有序实数对(1,-2,1)的特征多项式的乘积;
(3)若有序实数对(0,2,m)的特征多项式与有序实数对(0,n,2)的特征多项式的乘积的结果为6x2+x-2,求mn的值.
13.(2024七下·温州期中)先阅读下面的例题,再解决问题:例题:若,求m和n的值,解:
∵,
∴,
∴,
∵,
∴,
∴.
问题:
(1)若,求x和y的值.
(2)试探究关于x、y的代数式是否有最小值,若存在,求出最小值及此时x、y的值,说明理由.
14.(2024七下·温州期中)规定:形如关于,的方程与的两个方程互为共轭二元一次方程,其中.由这两个方程组成的方程组叫做共轭方程组,、称之为共轭系数.
(1)方程的共轭二元一次方程是______;
(2)若关于,的二元一次方程组为共轭方程,求此共轭方程组的共轭系数;
(3)对于共轭二元一次方程组,小聪通过探究发现,无论,为何值,解、一定相等.你同意他的结论吗?请说明理由.
15.(2024七下·金东期中)我们定义:一个整数能表示成(、是整数)的形式,则称这个数为“完美数”,例如,5是“完美数”,理由:因为,所以5是“完美数”.
【解决问题】
(1)已知29是“完美数”,请将它写成(、是整数)的形式__________;
(2)若可配方成(、为常数),则__________;
【探究问题】
(3)已知,则__________;
(4)已知(、是整数,是常数),要使为“完美数”,试求出符合条件的一个值,并说明理由.
【拓展结论】
(5)已知实数、满足,求的最小值.
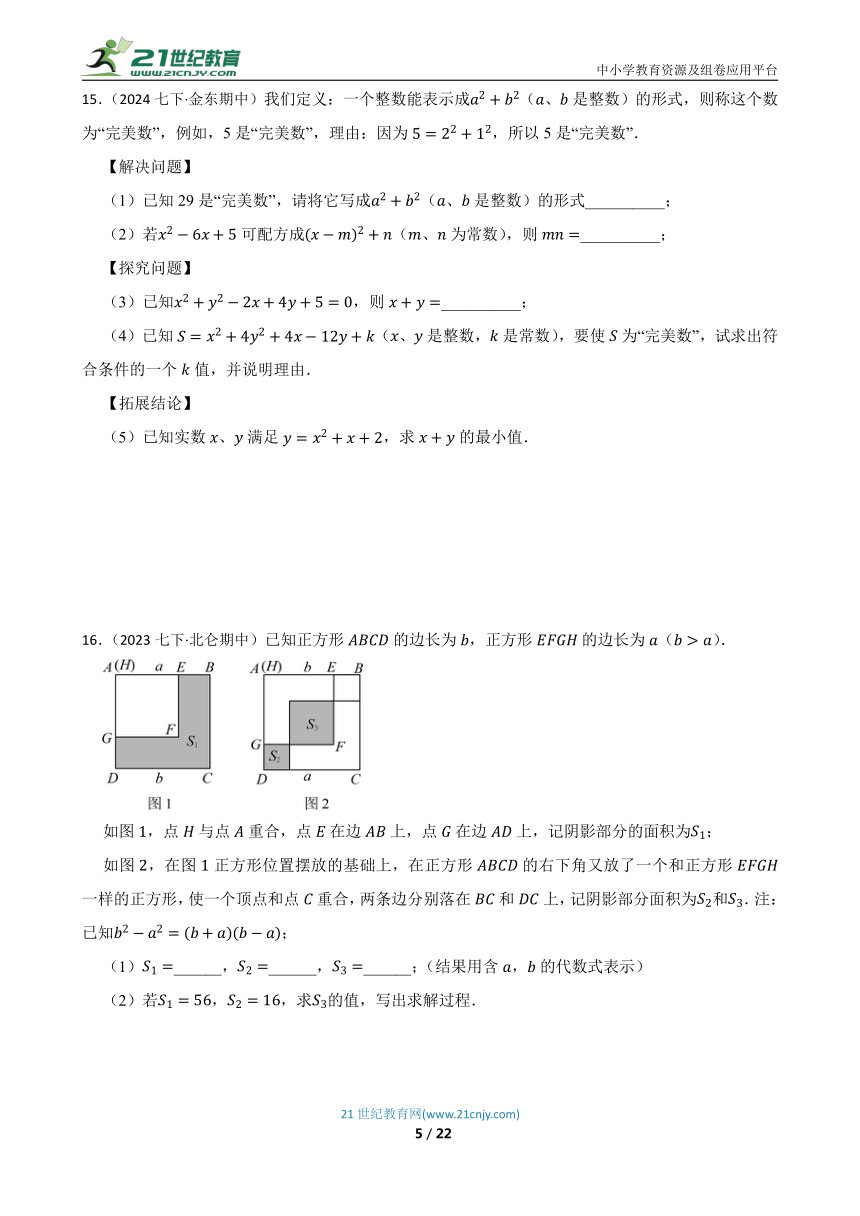
16.(2023七下·北仑期中)已知正方形的边长为,正方形的边长为().
如图,点与点重合,点在边上,点在边上,记阴影部分的面积为;
如图,在图正方形位置摆放的基础上,在正方形的右下角又放了一个和正方形一样的正方形,使一个顶点和点重合,两条边分别落在和上,记阴影部分面积为和.注:已知;
(1)______,______,______;(结果用含,的代数式表示)
(2)若,,求的值,写出求解过程.
17.(2024七下·宁海期中)阅读下列材料:教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.即将多项式(b、c为常数)写成(h、k为常数)的形式,配方法是一种重要的解决数学问题的方法,不仅可以将有些看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题及求代数式最大、最小值等问题.
【知识理解】:
(1)若多项式是一个完全平方式,那么常数k的值为 ;
(2)配方: ;
【知识运用】:
(3)已知,求m,n的值.
18.(2024七下·义乌期中)完全平方公式经过适当的变形,可以解决很多数学问题.例如:若,,求的值.
解:∵,,
∴,.
即.
∴.
根据上面的解题思路与方法解决下列问题:
(1),,则的值为 ;
(2)如图,C是线段上的一点,分别以,为边向两边作正方形,,两正方形面积的和为25,设,,求的面积;
19.(2024七下·新昌期中)阅读下列素材,完成相应的任务.
平衡多项式
素材一: 定义:对于一组多项式:,,(a,b,c都是非零常数),当其中一个多项式的平方与另外两个多项式的乘积的差是一个常数m时,称这样的三个多项式是一组平衡多项式,m的值是这组平衡多项式的平衡因子.
素材二: 例如:对于多项式,,, 因为, 所以多项式,,是一组平衡多项式,其平衡因子为1.
任务一: 小明发现多项式,,是一组平衡多项式,在求其平衡因子时,列式如下:,根据他的思路求该组平衡多项式的平衡因子.
任务二: 判断多项式,,是否为一组平衡多项式,若是,求出其平衡因子;若不是,说明理由.
任务三: 若多项式,,(p为非零常数)是一组平衡多项式,求p的值.
20.(2024七下·金东期中)几何和代数是密切相关的.
(1)如图 1, 这是由四个小长方形拼成的大长方形.我们发现:
12
所以得到等式:
上述等式的变形过程叫____________.
(2)利用图 2, 请你仿照上述的过程, 请把用两个多项式的乘积表示, 直接写出结果.
(3)如图3, 已有这些小长方形和小正方形.请你利用所有的图形拼出一个大的长方形, 并给出一个与 (1) 中结论类似的等式.
21.(2024七下·闽清期中)根据以下信息,探索完成任务:
如何设计招聘方案?
素材 某汽车制造厂开发一款新式电动汽车,计划一年生产安装辆每名熟练工均能独立安装电动汽车,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,经过培训上岗可以独立进行安装.
素材 调研部门发现:名熟练工和名新工人每月可安装辆电动汽车;名熟练工和名新工人每月可安装辆电动汽车.
素材 工厂给安装电动汽车的每名熟练工每月发元工资,每名新工人每月发元工资.
问题解决
任务一 分析数量关系 每名熟练工和新工人每月分别可以安装多少辆电动汽车?
任务二: 确定可行方案 如果工厂招聘名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种工人的招聘方案?
任务三: 选取最优方案 在上述方案中,为了节省成本,应该招聘新工人______ 名直接写出答案
答案解析部分
1.【答案】C
2.【答案】A
【解析】【解答】解:
=
,
因为不含的二次项,
所以,
而,
所以=-1,
故答案为:A.
【分析】先化简得到,根据不含项的系数为零求出2a-b=0,然后整体代入计算解题.
3.【答案】D
4.【答案】D
【解析】【解答】解:①:只有在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故①不符合题意;
②:只有当时,在实数范围内可表示成的形式,故②不符合题意;
③:因为任意非零数字的0次幂等于1,所以此时;又因为1的任意次幂都等于1,所以此时,故③符合题意;
④:由题意知,,则当时,总有,因为是任意实数,则有,即有方程组,解得:,故④符合题意;
综上,③④符合题意.
故选:D.
【分析】①平行公理的前提是在同一平面内;②实数范围内无法对平方和公式进行因式分解;③注意一些特殊的乘方运算,如正负1的乘方,0次幂等;④理解题意是关键,本题突破口是先求出关于的二元一次方程的特殊解,从而得到关于的二元一次方程组,解这个方程组即可.
5.【答案】B
【解析】【解答】解:设正方形A的边长为,正方形的边长为,
由题意得,,,
即,,
,
即正方形的面积为,
故选:B.
【分析】
先分别设出两正方形的边长,再利用割补法分别求出两个图形中的阴影部分面积,即可得出小正方形的面积.
6.【答案】B
【解析】【解答】解:由,可得:S2-S1=9,
由图①得:S矩形ABCD=S1+a2+b(AD-a),
由图②得:S矩形ABCD=S2+a2+b(AB-a),
∴S1+a2+b(AD-a)=S2+a2+b(AB-a),
∴S2-S1=b(AD-AB),
∵AD-AB=m,
∴mb=12.
故答案为:B.
【分析】由已知可得出,再利用正方形的边长和矩形ABCD的面积分别表示出和即可确定出那一项常量.
7.【答案】B
【解析】【解答】解:设长方形的长为a,宽为b,
由图1可得,(a+b)2-4ab=35,
即a2+b2=2ab+35①,
由图2可得,(2a+b)(a+2b)-5ab=102,
即a2+b2=51②,
由①②得,2ab+35=51,
所以ab=8,
即长方形的面积为8,
故答案为:B.
【分析】分别设出小长方形的长为a、宽为b,则图1中大正方形的边长为(a+b),小正方形的边长为(a-b);图2中大长方形的长为(2a+b)、宽为(a+2b),则利用两个阴影部分的面积可得到关于x、y的方程组,解方程组即可求出其面积.
8.【答案】B
【解析】【解答】解:设大长方形的宽为,
由图知,,
,
,
,
,
,
,
,
,
,
,
的值为.
故选:.
【分析】
为便于计算,先设大长方形的宽为,则两个阴影部分的面积和周长,,,均可表示出来,再利用已知的等量关系,利用整式的混合运算法则进行化简即可得出与的数量关系.
9.【答案】;;
【解析】【解答】(1)∵,互为相反数时
∴,
∴,
解得:,
故答案为:。
(2)由,
解得:,
∴,
故答案为:。
(3)由,
解得:,
∵,
∴,
∴,则,
解得:,
∴,
故答案为:.
【分析】(1)根据,互为相反数即x+y=0,代入x+y=2+a中,求出的值;
(2)加减消元法解二元一次方程组,求出x=2a-2,y=4-a。然后计算x+2y;
(3)根据求出=3的值,由(2)得x=2a-2,y=4-a代入2x+y=3中求出a,然后再计算。
10.【答案】
【解析】【解答】解:∵ PN∥QM,
∴ ∠AR1B=∠ABR1,
翻折1次时,∠R1BM=,;
翻折2次时,∠R2BR1=,;
……,
折叠次时,,.
故答案为:.
【分析】根据折叠的性质和平行线的性质可得,折叠次可得,然后根据四边形内角和即可求得.
11.【答案】解:设,
则原式
去括号,原式
则q-p=,
去括号,原式==
【解析】【分析】将复杂的表达式简化为更易处理的形式,设,将原式转化为,去括号得到最终结果即可.
12.【答案】(1)(3,2,1)
(2)解:有序实数对(1,2,1)的特征多项式为:
有序实数对(1,-2,1)的特征多项式为:
所以()()==
=
(3)解:由题意得:
或2n=6;2m=-2
mn=-12÷4=-3
所以mn=-3
【解析】【解答】解:(1)根据题意得: 多项式3x2+2x+1的特征系数对为 :(3,2,1);
故答案为:(3,2,1)
【分析】(1)根据特征系数对的定义直接得出结果;
(2)根据有序数对写出对应的多项式,恰好是完全平方,利用完全平方公式化简即可;
(3)根据有序数对写出含有m、n的多项式,再由其乘积为6x2+x-2即可得出结果.
(1)(3,2,1)
(2)有序实数对(1,2,1)的特征多项式为:
有序实数对(1,-2,1)的特征多项式为:
所以()()==
=
(3)由题意得:
所以.
13.【答案】(1)解:∵,
∴,
∴,,
;
答: x和y的值都等于-2
(2)解:∵
.
∵,
∴.
∴当时,
即当时,有最小值2019
【解析】【分析】(1)由于等式左边可以表示成两个完全平方式的和,且它们的和为0,因为平方式都是非负数,则每一个平方式都等于0,即有;
(2)由于可通过配方表示成两个完全平方式与常数2019的和,则当两个平方式都取最小值0时,原代数式有最小值2019,此时可分别求出 x、y的值 .
(1)解:∵,
∴,
∴,,
;
(2)解:∵
.
∵,
∴.
∴当时,
即当时,有最小值2019.
14.【答案】(1)
(2)解:∵关于,的二元一次方程组为共轭方程,,,
即
解得:
,,
则此共轭方程组的共轭系数为,;
(3)答:不同意,理由如下:
共轭二元一次方程组,
得:,
得:,
当,即时
则当时,无论为何值,与的值相等.
【解析】【解答】解:(1)方程的共辄二元一次方程是;
故答案为:;
【分析】
(1)根据共轭二元一次方程的定义可直接写出;
(2)根据共轭二元一次方程的定义可联立关于的二元一次方程组,解方程组即可求出共轭系数;
(2)先把当作常数求出方程组的解,若与相等,即可确定出的取值范围,最后再进行判断.
(1)解:方程的共辄二元一次方程是;
故答案为:;
(2)∵关于,的二元一次方程组为共轭方程,
,,
即
解得:
,,
则此共轭方程组的共轭系数为,;
(3)不同意,理由如下,
共轭二元一次方程组,
得:,
得:,
当,即时
则当时,无论为何值,与的值相等.
15.【答案】解:
(4)当时,为“完美数”,理由如下:
,
当时,,则,为完美数;
(5)∵,
∴,
∵,
∴,
∴当时,有最小值,最小值为1
【解析】【解答】解:(1),
故答案为:;
(2);
∴,,
∴;
故答案为:-12.
(3)∵,
∴,
∴,
∴,,
解得:,,
∴;
故答案为:-1.
【分析】(1)分析10以内各自然数平方的尾数特征,发现2与5的平方和恰好是29;
(2)当一个二次三项式的二次项系数为1时,可把常数项表示成一次项系数一半的平方与另一个常数的和,从而把这个整式表示成一个完全平方式与常数和的形式;
(3)先把常数项5表示成1与4的和,则恰好能把等式左边表示成两个完全平方式的和,由于两个非负数的和为0,则每一个非负数都等于0,可分别求出的值,则可求;
(4)由于完全平方公式的展开式是两数的平方和加上或减去这两数乘积的2倍,可先把常数表示成的形式,则由“完美数”的概念知,S是两个完全平方式的和,则(k-13)等于0 ;
(5)由于等于,由平方式的非负性可知其有最小值1.
16.【答案】(1);;
(2)解:,而,
,
,
,
,,
【解析】【解答】解:(1)解:图中阴影部分的面积,可以看作两个正方形的面积差,即,所以;
由拼图可知:面积为的正方形的边长为,因此;面积为的正方形的边长为,因此;
故答案为:,,;
【分析】(1)显然等于两个正方形的面积差,对应的正方形边长为,对应的正方形的边长为,依次表示出和 即可;
(2)由可求出,再由的值利用平方差公式可求出,则的值都可求,即可求.
(1)解:图中阴影部分的面积,可以看作两个正方形的面积差,即,所以;
由拼图可知:面积为的正方形的边长为,因此;面积为的正方形的边长为,因此;
故答案为:,,;
(2),而,
,
,
,
,,
.
17.【答案】(1)±4
(2)10
(3),
,,
∴,.
答:m,n的值分别是-4和4
【解析】【解答】解:(1)多项式是一个完全平方公式,
,
,
故答案为:;
(2)
,
故答案为:;
【分析】(1)由于完全平方公式的展开式是两数的平方和加上或减去这两数乘积的2倍,因为4是2的平方,所以;
(2)当一个二次三项式的二次项系数为1时,可把常数项表示成一次项系数一半的平方与另一个常数的和,从而把这个整式表示一个平方式与常数和的形式;
(3)先把表示成即可得到两个完全平方式,由于平方式都是非负数,则当两个非负数的和为0时,每个非负数都等于0,即可分别求出值.
18.【答案】(1)17
(2)解:设,,
根据题意可知,,
,
,
,
,
.
【解析】【解答】(1)解:,,
,,
;
故答案为:17;
【分析】(1)根据题意,,代入计算即可求得;
(2)根据题意可知,,求出,再根据三角形的面积公式计算即可.
19.【答案】【解答】
解:
任务一:,
答:该组平衡多项式的平衡因子为4;
任务二:,
答:该组多项式是平衡多项式,其平衡因子为9;
任务三:①当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
②当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
③当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
综上,或.
【解析】【分析】任务一:利用整式的加减乘除混合运算顺序进行计算即可,运算时注意灵活运用乘法公式可简化计算;
任务二:利用整式的加减乘除混合运算顺序进行计算即可;
任务三:由平衡多项式概念知,三个多项式中肯定存在一个多项式的完全平方减去剩余两个之积等于一个常数,因此存在三种情况,应分别计算.
20.【答案】(1)因式分解
(2)
(3)解:如图所示
,
∵,
又∵
∴有等式:,
故答案为:
【解析】【解答】解(1):把一个多项式表示成几个因式乘积的形式,这种变形叫作因式分解;
故答案为:因式分解;
(2)∵,又∵
∴,
故答案为:;
【分析】(1)由因式分解的概念直接填写答案即可;
(2)由长方形面积的可借助(1)中的方法表示,即通过面积相等建立等式即可;
(3)方法不唯一,只要能拼出长方形即可运用(1)中的方法进行表示,注意正方形的个数肯定是某个自然数的平方.
(1)根据因式分解的定义可知:等式变形过程叫:因式分解,
故答案为:因式分解;
(2)∵,
又∵
∴,
故答案为:;
(3)结合已知的矩形形状,作出的图:
,
∵,
又∵
∴有等式:,
故答案为:.
21.【答案】解:任务一:设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,
由题意得:,解得:,
答:每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车.
任务二:设抽调熟练工名,招聘新工人名,
由题意得:,
整理得:,
、为正整数,且,
或,
有种工人的招聘方案:
抽调熟练工名,招聘新工人名;
抽调熟练工名,招聘新工人名.
任务三:方案中,发放工资为:元;
方案中,发放工资为:元;
,
为了节省成本,应该抽调熟练工名,招聘新工人名.
故答案为:.
【解析】【分析】任务一:先设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,根据等量关系“名熟练工和名新工人每月可安装辆电动汽车”和“名熟练工和名新工人每月可安装辆电动汽车”列出二元一次方程组求解即可;
任务二:设抽调熟练工名,招聘新工人名,根据“招聘的新工人和抽调的熟练工刚好能完成一年的安装任务”列出二元一次方程,求出符合题意的正整数解即可;
任务三:求出方案和方案的成本,然后比较即可解答.
21世纪教育网(www.21cnjy.com)
1 / 1
七下期中拓展培优卷
一、选择题
1.(2023七下·北仑期中)如图,当光线从空气进入水中时,会发生折射,满足入射角与折射角的度数比为,如图,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面夹角分别为,,在水中两条折射光线的夹角为,则,,三者之间的数量关系为( )
A. B.
C. D.
2.(2024七下·杭州期中)已知,是常数,若化简的结果不含的二次项,则的值为( )
A. B. C. D.
3.(2025七下·嘉兴月考)小宸的综合实践活动报告部分信息如下图,则用十六进制表示的结果是( )
综合实践活动:寻找数和计算工具的发展足迹
十六进制:缝十六进一,采用数字和字母共16个计数符号.
十六进制的符号和十进制的数的对应关系:
16进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
10进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例:,
A.182 B.DE C. D.
4.(2024七下·温州期中)①过一点有且只有一条直线与已知直线平行;
②无论取何实数,多项式总能分解成两个一次因式积的形式;
③若,则可以取的值有2个;
④关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,其中当每取一个值时,就有一个方程,而这些方程总有一个公共解,则这个公共解是.其中正确的有( )
A.①③ B.①④ C.②④ D.③④
5.(2024七下·嘉善期中)有两个正方形A、,将A,并列放置后构造新的图形,分别得到长方形图甲与正方形图乙若图甲、图乙中阴影的面积分别为与,则正方形的面积为( )
A. B. C. D.
6.(2024七下·宁海期中)矩形内放入两张边长分别为和的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为.已知,,设,则下列值是常数的是( )
A. B. C. D.
7.(2024七下·金东期中)有若干个大小形状完全相同的小长方形现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为35;其中5个如图2摆放,构造出一个长方形,其中阴影部分面积为102(各个小长方形之间不重叠不留空),则每个小长方形的面积为( )
A.4 B.8 C.12 D.16
8.(2024七下·镇海区期末)如图,有三张正方形纸片,,,它们的边长分别为,,,将三张纸片按图,图两种不同方式放置于同一长方形中,记图中阴影部分周长为,面积为,图中阴影部分周长为,面积为,若,则的值为( )
A. B. C. D.
二、填空题
9.(2024七下·杭州期中)已知关于,的方程组,
(1),互为相反数时, ;
(2) ;
(3)若,满足,则 .
10.(2024七下·义乌期中)如图1是一张足够长的纸条,其中,点A、B分别在、上,记.如图2,将纸条折叠,使与重合,得折痕,如图3,将纸条展开后再折叠,使与重合,得折痕,将纸条展开后继续折叠,使与重合,得折痕…依此类推,第次折叠后, (用含α和n的代数式表示)
三、解答题
11.(2025七下·嘉兴月考)计算:.
12.(2024七下·杭州期中)给出如下定义:我们把有序实数对(a,b,c)叫做关于x的二次多项式ax2+bx+c的特征系数对,把关于x的二次多项式ax2+bx+c叫做有序实数对(a,b,c)的特征多项式.
(1)关于x的二次多项式3x2+2x+1的特征系数对为____________________;
(2)求有序实数对(1,2,1)的特征多项式与有序实数对(1,-2,1)的特征多项式的乘积;
(3)若有序实数对(0,2,m)的特征多项式与有序实数对(0,n,2)的特征多项式的乘积的结果为6x2+x-2,求mn的值.
13.(2024七下·温州期中)先阅读下面的例题,再解决问题:例题:若,求m和n的值,解:
∵,
∴,
∴,
∵,
∴,
∴.
问题:
(1)若,求x和y的值.
(2)试探究关于x、y的代数式是否有最小值,若存在,求出最小值及此时x、y的值,说明理由.
14.(2024七下·温州期中)规定:形如关于,的方程与的两个方程互为共轭二元一次方程,其中.由这两个方程组成的方程组叫做共轭方程组,、称之为共轭系数.
(1)方程的共轭二元一次方程是______;
(2)若关于,的二元一次方程组为共轭方程,求此共轭方程组的共轭系数;
(3)对于共轭二元一次方程组,小聪通过探究发现,无论,为何值,解、一定相等.你同意他的结论吗?请说明理由.
15.(2024七下·金东期中)我们定义:一个整数能表示成(、是整数)的形式,则称这个数为“完美数”,例如,5是“完美数”,理由:因为,所以5是“完美数”.
【解决问题】
(1)已知29是“完美数”,请将它写成(、是整数)的形式__________;
(2)若可配方成(、为常数),则__________;
【探究问题】
(3)已知,则__________;
(4)已知(、是整数,是常数),要使为“完美数”,试求出符合条件的一个值,并说明理由.
【拓展结论】
(5)已知实数、满足,求的最小值.
16.(2023七下·北仑期中)已知正方形的边长为,正方形的边长为().
如图,点与点重合,点在边上,点在边上,记阴影部分的面积为;
如图,在图正方形位置摆放的基础上,在正方形的右下角又放了一个和正方形一样的正方形,使一个顶点和点重合,两条边分别落在和上,记阴影部分面积为和.注:已知;
(1)______,______,______;(结果用含,的代数式表示)
(2)若,,求的值,写出求解过程.
17.(2024七下·宁海期中)阅读下列材料:教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.即将多项式(b、c为常数)写成(h、k为常数)的形式,配方法是一种重要的解决数学问题的方法,不仅可以将有些看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题及求代数式最大、最小值等问题.
【知识理解】:
(1)若多项式是一个完全平方式,那么常数k的值为 ;
(2)配方: ;
【知识运用】:
(3)已知,求m,n的值.
18.(2024七下·义乌期中)完全平方公式经过适当的变形,可以解决很多数学问题.例如:若,,求的值.
解:∵,,
∴,.
即.
∴.
根据上面的解题思路与方法解决下列问题:
(1),,则的值为 ;
(2)如图,C是线段上的一点,分别以,为边向两边作正方形,,两正方形面积的和为25,设,,求的面积;
19.(2024七下·新昌期中)阅读下列素材,完成相应的任务.
平衡多项式
素材一: 定义:对于一组多项式:,,(a,b,c都是非零常数),当其中一个多项式的平方与另外两个多项式的乘积的差是一个常数m时,称这样的三个多项式是一组平衡多项式,m的值是这组平衡多项式的平衡因子.
素材二: 例如:对于多项式,,, 因为, 所以多项式,,是一组平衡多项式,其平衡因子为1.
任务一: 小明发现多项式,,是一组平衡多项式,在求其平衡因子时,列式如下:,根据他的思路求该组平衡多项式的平衡因子.
任务二: 判断多项式,,是否为一组平衡多项式,若是,求出其平衡因子;若不是,说明理由.
任务三: 若多项式,,(p为非零常数)是一组平衡多项式,求p的值.
20.(2024七下·金东期中)几何和代数是密切相关的.
(1)如图 1, 这是由四个小长方形拼成的大长方形.我们发现:
12
所以得到等式:
上述等式的变形过程叫____________.
(2)利用图 2, 请你仿照上述的过程, 请把用两个多项式的乘积表示, 直接写出结果.
(3)如图3, 已有这些小长方形和小正方形.请你利用所有的图形拼出一个大的长方形, 并给出一个与 (1) 中结论类似的等式.
21.(2024七下·闽清期中)根据以下信息,探索完成任务:
如何设计招聘方案?
素材 某汽车制造厂开发一款新式电动汽车,计划一年生产安装辆每名熟练工均能独立安装电动汽车,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,经过培训上岗可以独立进行安装.
素材 调研部门发现:名熟练工和名新工人每月可安装辆电动汽车;名熟练工和名新工人每月可安装辆电动汽车.
素材 工厂给安装电动汽车的每名熟练工每月发元工资,每名新工人每月发元工资.
问题解决
任务一 分析数量关系 每名熟练工和新工人每月分别可以安装多少辆电动汽车?
任务二: 确定可行方案 如果工厂招聘名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种工人的招聘方案?
任务三: 选取最优方案 在上述方案中,为了节省成本,应该招聘新工人______ 名直接写出答案
答案解析部分
1.【答案】C
2.【答案】A
【解析】【解答】解:
=
,
因为不含的二次项,
所以,
而,
所以=-1,
故答案为:A.
【分析】先化简得到,根据不含项的系数为零求出2a-b=0,然后整体代入计算解题.
3.【答案】D
4.【答案】D
【解析】【解答】解:①:只有在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故①不符合题意;
②:只有当时,在实数范围内可表示成的形式,故②不符合题意;
③:因为任意非零数字的0次幂等于1,所以此时;又因为1的任意次幂都等于1,所以此时,故③符合题意;
④:由题意知,,则当时,总有,因为是任意实数,则有,即有方程组,解得:,故④符合题意;
综上,③④符合题意.
故选:D.
【分析】①平行公理的前提是在同一平面内;②实数范围内无法对平方和公式进行因式分解;③注意一些特殊的乘方运算,如正负1的乘方,0次幂等;④理解题意是关键,本题突破口是先求出关于的二元一次方程的特殊解,从而得到关于的二元一次方程组,解这个方程组即可.
5.【答案】B
【解析】【解答】解:设正方形A的边长为,正方形的边长为,
由题意得,,,
即,,
,
即正方形的面积为,
故选:B.
【分析】
先分别设出两正方形的边长,再利用割补法分别求出两个图形中的阴影部分面积,即可得出小正方形的面积.
6.【答案】B
【解析】【解答】解:由,可得:S2-S1=9,
由图①得:S矩形ABCD=S1+a2+b(AD-a),
由图②得:S矩形ABCD=S2+a2+b(AB-a),
∴S1+a2+b(AD-a)=S2+a2+b(AB-a),
∴S2-S1=b(AD-AB),
∵AD-AB=m,
∴mb=12.
故答案为:B.
【分析】由已知可得出,再利用正方形的边长和矩形ABCD的面积分别表示出和即可确定出那一项常量.
7.【答案】B
【解析】【解答】解:设长方形的长为a,宽为b,
由图1可得,(a+b)2-4ab=35,
即a2+b2=2ab+35①,
由图2可得,(2a+b)(a+2b)-5ab=102,
即a2+b2=51②,
由①②得,2ab+35=51,
所以ab=8,
即长方形的面积为8,
故答案为:B.
【分析】分别设出小长方形的长为a、宽为b,则图1中大正方形的边长为(a+b),小正方形的边长为(a-b);图2中大长方形的长为(2a+b)、宽为(a+2b),则利用两个阴影部分的面积可得到关于x、y的方程组,解方程组即可求出其面积.
8.【答案】B
【解析】【解答】解:设大长方形的宽为,
由图知,,
,
,
,
,
,
,
,
,
,
,
的值为.
故选:.
【分析】
为便于计算,先设大长方形的宽为,则两个阴影部分的面积和周长,,,均可表示出来,再利用已知的等量关系,利用整式的混合运算法则进行化简即可得出与的数量关系.
9.【答案】;;
【解析】【解答】(1)∵,互为相反数时
∴,
∴,
解得:,
故答案为:。
(2)由,
解得:,
∴,
故答案为:。
(3)由,
解得:,
∵,
∴,
∴,则,
解得:,
∴,
故答案为:.
【分析】(1)根据,互为相反数即x+y=0,代入x+y=2+a中,求出的值;
(2)加减消元法解二元一次方程组,求出x=2a-2,y=4-a。然后计算x+2y;
(3)根据求出=3的值,由(2)得x=2a-2,y=4-a代入2x+y=3中求出a,然后再计算。
10.【答案】
【解析】【解答】解:∵ PN∥QM,
∴ ∠AR1B=∠ABR1,
翻折1次时,∠R1BM=,;
翻折2次时,∠R2BR1=,;
……,
折叠次时,,.
故答案为:.
【分析】根据折叠的性质和平行线的性质可得,折叠次可得,然后根据四边形内角和即可求得.
11.【答案】解:设,
则原式
去括号,原式
则q-p=,
去括号,原式==
【解析】【分析】将复杂的表达式简化为更易处理的形式,设,将原式转化为,去括号得到最终结果即可.
12.【答案】(1)(3,2,1)
(2)解:有序实数对(1,2,1)的特征多项式为:
有序实数对(1,-2,1)的特征多项式为:
所以()()==
=
(3)解:由题意得:
或2n=6;2m=-2
mn=-12÷4=-3
所以mn=-3
【解析】【解答】解:(1)根据题意得: 多项式3x2+2x+1的特征系数对为 :(3,2,1);
故答案为:(3,2,1)
【分析】(1)根据特征系数对的定义直接得出结果;
(2)根据有序数对写出对应的多项式,恰好是完全平方,利用完全平方公式化简即可;
(3)根据有序数对写出含有m、n的多项式,再由其乘积为6x2+x-2即可得出结果.
(1)(3,2,1)
(2)有序实数对(1,2,1)的特征多项式为:
有序实数对(1,-2,1)的特征多项式为:
所以()()==
=
(3)由题意得:
所以.
13.【答案】(1)解:∵,
∴,
∴,,
;
答: x和y的值都等于-2
(2)解:∵
.
∵,
∴.
∴当时,
即当时,有最小值2019
【解析】【分析】(1)由于等式左边可以表示成两个完全平方式的和,且它们的和为0,因为平方式都是非负数,则每一个平方式都等于0,即有;
(2)由于可通过配方表示成两个完全平方式与常数2019的和,则当两个平方式都取最小值0时,原代数式有最小值2019,此时可分别求出 x、y的值 .
(1)解:∵,
∴,
∴,,
;
(2)解:∵
.
∵,
∴.
∴当时,
即当时,有最小值2019.
14.【答案】(1)
(2)解:∵关于,的二元一次方程组为共轭方程,,,
即
解得:
,,
则此共轭方程组的共轭系数为,;
(3)答:不同意,理由如下:
共轭二元一次方程组,
得:,
得:,
当,即时
则当时,无论为何值,与的值相等.
【解析】【解答】解:(1)方程的共辄二元一次方程是;
故答案为:;
【分析】
(1)根据共轭二元一次方程的定义可直接写出;
(2)根据共轭二元一次方程的定义可联立关于的二元一次方程组,解方程组即可求出共轭系数;
(2)先把当作常数求出方程组的解,若与相等,即可确定出的取值范围,最后再进行判断.
(1)解:方程的共辄二元一次方程是;
故答案为:;
(2)∵关于,的二元一次方程组为共轭方程,
,,
即
解得:
,,
则此共轭方程组的共轭系数为,;
(3)不同意,理由如下,
共轭二元一次方程组,
得:,
得:,
当,即时
则当时,无论为何值,与的值相等.
15.【答案】解:
(4)当时,为“完美数”,理由如下:
,
当时,,则,为完美数;
(5)∵,
∴,
∵,
∴,
∴当时,有最小值,最小值为1
【解析】【解答】解:(1),
故答案为:;
(2);
∴,,
∴;
故答案为:-12.
(3)∵,
∴,
∴,
∴,,
解得:,,
∴;
故答案为:-1.
【分析】(1)分析10以内各自然数平方的尾数特征,发现2与5的平方和恰好是29;
(2)当一个二次三项式的二次项系数为1时,可把常数项表示成一次项系数一半的平方与另一个常数的和,从而把这个整式表示成一个完全平方式与常数和的形式;
(3)先把常数项5表示成1与4的和,则恰好能把等式左边表示成两个完全平方式的和,由于两个非负数的和为0,则每一个非负数都等于0,可分别求出的值,则可求;
(4)由于完全平方公式的展开式是两数的平方和加上或减去这两数乘积的2倍,可先把常数表示成的形式,则由“完美数”的概念知,S是两个完全平方式的和,则(k-13)等于0 ;
(5)由于等于,由平方式的非负性可知其有最小值1.
16.【答案】(1);;
(2)解:,而,
,
,
,
,,
【解析】【解答】解:(1)解:图中阴影部分的面积,可以看作两个正方形的面积差,即,所以;
由拼图可知:面积为的正方形的边长为,因此;面积为的正方形的边长为,因此;
故答案为:,,;
【分析】(1)显然等于两个正方形的面积差,对应的正方形边长为,对应的正方形的边长为,依次表示出和 即可;
(2)由可求出,再由的值利用平方差公式可求出,则的值都可求,即可求.
(1)解:图中阴影部分的面积,可以看作两个正方形的面积差,即,所以;
由拼图可知:面积为的正方形的边长为,因此;面积为的正方形的边长为,因此;
故答案为:,,;
(2),而,
,
,
,
,,
.
17.【答案】(1)±4
(2)10
(3),
,,
∴,.
答:m,n的值分别是-4和4
【解析】【解答】解:(1)多项式是一个完全平方公式,
,
,
故答案为:;
(2)
,
故答案为:;
【分析】(1)由于完全平方公式的展开式是两数的平方和加上或减去这两数乘积的2倍,因为4是2的平方,所以;
(2)当一个二次三项式的二次项系数为1时,可把常数项表示成一次项系数一半的平方与另一个常数的和,从而把这个整式表示一个平方式与常数和的形式;
(3)先把表示成即可得到两个完全平方式,由于平方式都是非负数,则当两个非负数的和为0时,每个非负数都等于0,即可分别求出值.
18.【答案】(1)17
(2)解:设,,
根据题意可知,,
,
,
,
,
.
【解析】【解答】(1)解:,,
,,
;
故答案为:17;
【分析】(1)根据题意,,代入计算即可求得;
(2)根据题意可知,,求出,再根据三角形的面积公式计算即可.
19.【答案】【解答】
解:
任务一:,
答:该组平衡多项式的平衡因子为4;
任务二:,
答:该组多项式是平衡多项式,其平衡因子为9;
任务三:①当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
②当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
③当
时,
∵多项式,,(p为非零常数)是一组平衡多项式,
∴,
解得:,
综上,或.
【解析】【分析】任务一:利用整式的加减乘除混合运算顺序进行计算即可,运算时注意灵活运用乘法公式可简化计算;
任务二:利用整式的加减乘除混合运算顺序进行计算即可;
任务三:由平衡多项式概念知,三个多项式中肯定存在一个多项式的完全平方减去剩余两个之积等于一个常数,因此存在三种情况,应分别计算.
20.【答案】(1)因式分解
(2)
(3)解:如图所示
,
∵,
又∵
∴有等式:,
故答案为:
【解析】【解答】解(1):把一个多项式表示成几个因式乘积的形式,这种变形叫作因式分解;
故答案为:因式分解;
(2)∵,又∵
∴,
故答案为:;
【分析】(1)由因式分解的概念直接填写答案即可;
(2)由长方形面积的可借助(1)中的方法表示,即通过面积相等建立等式即可;
(3)方法不唯一,只要能拼出长方形即可运用(1)中的方法进行表示,注意正方形的个数肯定是某个自然数的平方.
(1)根据因式分解的定义可知:等式变形过程叫:因式分解,
故答案为:因式分解;
(2)∵,
又∵
∴,
故答案为:;
(3)结合已知的矩形形状,作出的图:
,
∵,
又∵
∴有等式:,
故答案为:.
21.【答案】解:任务一:设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,
由题意得:,解得:,
答:每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车.
任务二:设抽调熟练工名,招聘新工人名,
由题意得:,
整理得:,
、为正整数,且,
或,
有种工人的招聘方案:
抽调熟练工名,招聘新工人名;
抽调熟练工名,招聘新工人名.
任务三:方案中,发放工资为:元;
方案中,发放工资为:元;
,
为了节省成本,应该抽调熟练工名,招聘新工人名.
故答案为:.
【解析】【分析】任务一:先设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,根据等量关系“名熟练工和名新工人每月可安装辆电动汽车”和“名熟练工和名新工人每月可安装辆电动汽车”列出二元一次方程组求解即可;
任务二:设抽调熟练工名,招聘新工人名,根据“招聘的新工人和抽调的熟练工刚好能完成一年的安装任务”列出二元一次方程,求出符合题意的正整数解即可;
任务三:求出方案和方案的成本,然后比较即可解答.
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
