期中评价试题 2024--2025学年小学数学人教版五年级下册
文档属性
| 名称 | 期中评价试题 2024--2025学年小学数学人教版五年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 400.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中评价试题 2024--2025学年小学数学人教版五年级下册
一、选择题
1.同学们用不同的方式表示自己对的理解,其中正确的有( )。
A.①③ B.②④ C.①②③ D.①③④
2.下面的分数中,不能化成有限小数的是( )。
A. B. C. D.
3.将的分子加上6,要使分数的大小不变,分母应( )。
A.加上6 B.增加2倍 C.加上21 D.扩大到原来的3倍
4.正方体的棱长扩大2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。括号里依次应填入( )。
A.2;8 B.4;8 C.6;8 D.8;4
5.一个棱长是30cm的正方体盒子里面装了一些水,水深20cm,将一块石头完全浸入水中,水面上升了4cm,这块石头的体积是( )cm3。
A.1600 B.2400 C.3600 D.18000
二、填空题
6.51的因数有( ),在这些因数中既是奇数又是质数的有( )。
7.3900平方厘米=( )平方米 5立方米6立方分米=( )立方米
8.同时是2、3、5的倍数的最大两位数是( ),同时有因数2、3、5的最小三位数是( )。
9.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
10.把7米长的铁丝平均截成9段,每段长( )米,每段是全长的( )。
11.
12.把一个长60cm,宽40cm,高30cm的长方体木块削成一个体积最大的正方体,削去部分的体积是( )cm3。
13.一个立体图形,从上面看到的图形是,从前面看到的图形是,摆这个立体图形至少需要( )个正方体小块。
14.把2个棱长为3cm的正方体拼成一个长方体,这个长方体的表面积是( )cm2,体积是( )cm3。
三、计算题
15.直接写出得数。
63= 6×3= 6+6+6= 2.3×1.9=
0.5×0.5= 6.7×0.25= 5.13÷3= 29÷18=
16.简算下面各题。
857×1.9-8.57×80-85.7 12.5×32×2.5
17.求下列图形的表面积和体积。
四、作图题
18.请在括号里写出一个分数,并在图中涂一涂表示出来。
( ) ( ) ( )
19.在方格纸上画出正方体的展开图。(每格代表1厘米)
五、解答题
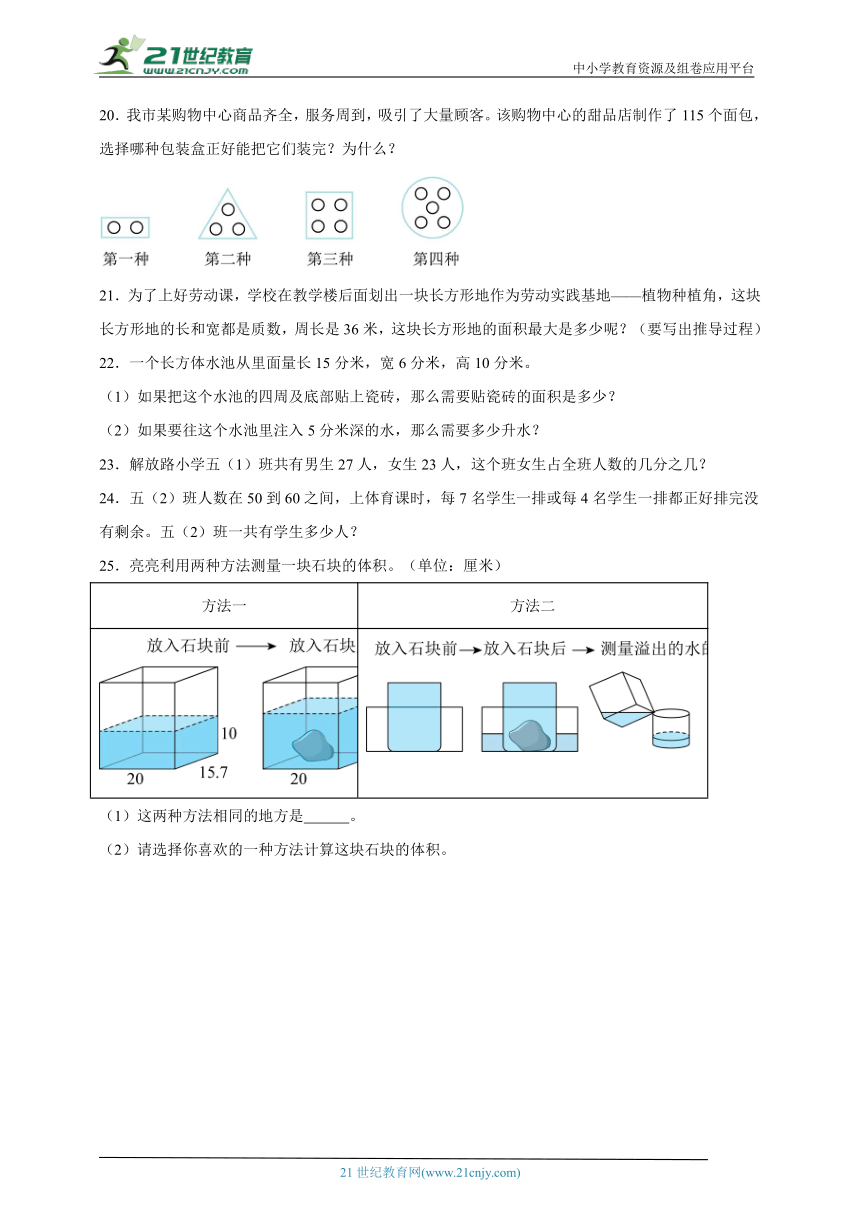
20.我市某购物中心商品齐全,服务周到,吸引了大量顾客。该购物中心的甜品店制作了115个面包,选择哪种包装盒正好能把它们装完?为什么?
21.为了上好劳动课,学校在教学楼后面划出一块长方形地作为劳动实践基地——植物种植角,这块长方形地的长和宽都是质数,周长是36米,这块长方形地的面积最大是多少呢?(要写出推导过程)
22.一个长方体水池从里面量长15分米,宽6分米,高10分米。
(1)如果把这个水池的四周及底部贴上瓷砖,那么需要贴瓷砖的面积是多少?
(2)如果要往这个水池里注入5分米深的水,那么需要多少升水?
23.解放路小学五(1)班共有男生27人,女生23人,这个班女生占全班人数的几分之几?
24.五(2)班人数在50到60之间,上体育课时,每7名学生一排或每4名学生一排都正好排完没有剩余。五(2)班一共有学生多少人?
25.亮亮利用两种方法测量一块石块的体积。(单位:厘米)
方法一 方法二
(1)这两种方法相同的地方是 。
(2)请选择你喜欢的一种方法计算这块石块的体积。
参考答案
1.D
分数的意义:把一个物体或一些物体看作一个整体,即单位“1”,平均分成若干份,表示其中的1份或几份的数,分母表示分成的份数,分子表示取出的份数;分数与除法的关系:被除数相当于分子,除号相当于分数线,除数相当于分母,据此解答。
①5÷4=
白纸条是4份,灰纸条是5份,即灰纸条的长度正好是白纸条的;
②4÷5=
线段的总长度是4,平均分成5份,其中的1段是;
③5÷4=(张)
把5张饼看作一个整体,即单位“1”;平均分成4份,每人分得张;
④5÷4=
把1看作单位“1”,平均分成4份,其中的5份表示。
正确的是①③④,共3个。
故答案为:D
2.D
分数化成小数:用分子去除分母,能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位数。
=3÷5=0.6
=7÷32=0.21875
=21÷35=0.6
=5÷12=0.4166…
因此不能化成有限小数的是。
故答案为:D
3.D
根据分数的基本性质,分子和分母同时乘或除以相同的数(0除外),分数的大小不变;将的分子加上6,分子由原来的3变成(3+6=9),相当于分子乘3,结合各选项的内容,逐项进行分析,据此解答。
A.分母加上6,现在的分数为,分数的大小发生改变,不符合题意;
B.分母增加2倍,现在的分数为,分数的大小发生改变,不符合题意;
C.分母加上21,现在的分数为,分数的大小发生改变,不符合题意;
D.分母扩大到原来的3倍,现在的分数为,分数的大小不变,符合题意。
故答案为:D
4.B
根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长可知,正方体的棱长扩大2倍,表面积扩大到原来的(2×2)倍,体积扩大到原来的(2×2×2)倍,据此解答。
2×2=4
2×2×2=8
正方体的棱长扩大2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:B
5.C
由题意可知,上升的水的体积等于这块石头的体积,上升的水的体积可以看成长是30cm,宽是30cm,高是4cm的长方体的体积,根据,代入数据计算即可。
(cm3)
一个棱长是30cm的正方体盒子里面装了一些水,水深20cm,将一块石头完全浸入水中,水面上升了4cm,这块石头的体积是3600cm3。
故答案为:C
6. 1、3、17、51 3、17
求一个数的因数时,就用这个数从1开始去整除,一直除到除数和商交换位置或除数和商相同为止,除数和商都是被除数的因数,重复的因数只写一个;整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数;一个数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,1既不是质数也不是合数;先列举出51的所有因数,再从里面找出既是奇数又是质数的数,据此解答。
51÷1=51
51÷3=17
所以,51的因数有1、3、17、51,在这些因数中既是奇数又是质数的有3、17。
7. 0.39 5.006
1平方米=10000平方厘米 1立方米=1000立方分米
高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率。据此解答。
1平方米=10000平方厘米 3900÷10000=0.39 3900平方厘米=0.39平方米
1立方米=1000立方分米 6÷1000=0.006 5立方米6立方分米=5.006立方米
8. 90 120
2,3,5的倍数的特征:个位上的数字是0,各个数位上的数字的和是3的倍数的数。
同时是2、3、5的倍数的最大两位数是90,同时有因数2、3、5的最小三位数是120。
9. ② ③
观察图形,再添加一个同样的小方块,从左面看到的图形不变,说明从左面看不到某位置上新放的小方块,据此得出添加的小方块放在②号位置上;
再添加一个同样的小方块,从前面看到的图形不变,说明从前面看不到某位置上新放的小方块,据此得出添加的小方块应放在③号位置上。
如图:
在②号位置上面放一个同样的小方块,从左面看:
在③号位置上面放一个同样的小方块,从前面看:
填空如下:
在 ② 号位置上面放一个同样的小方块,从左面看到的图形不变,在 ③ 号位置上面放一个同样的小方块,从前面看到的图形不变。
10.
求每段长多少米,用铁丝的长度÷平均截的段数;把铁丝的全长看作单位“1”,平均分成9段,求每段是全长的几分之几,用1÷9解答。
7÷9=(米)
1÷9=
把7米长的铁丝平均截成9段,每段长米,每段是全长的。
11.2;12;10;6
(1)的分子和分母同时除以3求出分子,根据分数与除法的关系把转化为除法,再利用商不变的规律求出除数;
(2)根据分数与除法的关系把2÷5转化为分数,再利用“分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变”求出分母和分子,据此解答。
(1)
=2÷3=(2×4)÷(3×4)=8÷12
所以,==8÷12。
(2)2÷5=
所以,==2÷5。
12.45000
分析题目,削成的最大的正方体的棱长等于长方体的最短边即30cm,削去部分的体积等于长方体的体积减去正方体的体积,据此结合长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长代入数据列式计算即可。
60×40×30-30×30×30
=2400×30-900×30
=72000-27000
=45000(cm3)
把一个长60cm,宽40cm,高30cm的长方体木块削成一个体积最大的正方体,削去部分的体积是45000cm3。
13.11
根据从上面看到的图形可知,这个立体图形底下一层有9个正方体小块。再根据从前面看到的图形可知,上面一层至少有2个正方体小块。据此解题。
9+2=11(个)
所以,摆这个立体图形至少需要11个正方体小块。
14. 90 54
由题意可知,拼成的长方体的长是cm,宽是3cm,高是3cm,根据、,代入数据计算即可得解。
(cm2)
(cm3)
把2个棱长为3cm的正方体拼成一个长方体,这个长方体的表面积是90cm2,体积是54cm3。
15.216;18;18;4.37;
0.25;1.675;1.71;
略
16.857;9;1000
第一题将857×1.9写成8.57×190,把85.7写成8.57×10,再利用乘法分配律进行简便计算即可;
第二题利用加法交换律、结合律及减法的性质进行简便计算即可;
第三题先将32写成8×4,再利用结合律分别计算12.5×8和4×2.5,最后把这两个结果相乘即可。
857×1.9-8.57×80-85.7
=8.57×190-8.57×80-8.57×10
=8.57×(190-80-10)
=8.57×100
=857
=(6.75+3.25)-()
=10-1
=9
12.5×32×2.5
=12.5×8×4×2.5
=(12.5×8)×(4×2.5)
=100×10
=1000
17.表面积470cm2;体积600cm3
表面积384cm2;体积512cm3
(1)图形是一个长为8cm,宽为5cm,高为15cm的长方体,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入相应数值计算;
(2)图形是一个棱长为8cm的正方体,根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入相应数值计算。
表面积:(8×5+8×15+5×15)×2
=(40+120+75)×2
=235×2
=470(cm2)
体积:8×5×15
=40×15
=600(cm3)
图形的表面积是470cm2,体积是600cm3。
表面积:8×8×6
=64×6
=384(cm2)
体积:8×8×8
=64×8
=512(cm3)
图形的表面积是384cm2,体积是512cm3。
18.见详解
先写合适的分数,再根据分数的意义涂色即可;
表示把8个圆圈看作一个整体,平均分成8份,取其中的7份涂色;
表示把大三角形看作一个整体,平均分成4份,取其中的1份涂色;
表示把圆看作一个整体,平均分成4份,取其中的3份涂色;
据此解答即可。
(答案不唯一)
19.见详解
正方体表面展开图有11种情况画出一种即可。
1-4-1型 (6种):中间一行有4个正方形,上下各接1个正方形。通过调整上下两个正方形的位置,形成6种不同的图形。
2-3-1型 (3种):第一行有2个正方形,中间一行有3个,最后一行有1个,通过不同连接方式产生3种图形。
3-3型 (1种):上下两行各3个正方形,呈阶梯状排列。
2-2-2型 (1种):三行各2个正方形,呈“Z”字形排列。
由分析可作图11种:
将其中一种画在方格纸上
(答案不唯一)
20.选择第四种包装盒正好能把它们装完;因为115是5的倍数
面包的总个数是每个包装盒装面包的个数的倍数,就选择哪种包装盒,据此解答。
第一种:115÷2=57(盒)……1(个),115不是2的倍数,不符合题意。
第二种:115÷3=38(盒)……1(个),115不是3的倍数,不符合题意。
第三种:115÷4=28(盒)……3(个),115不是4的倍数,不符合题意。
第四种:115÷5=23(盒),115是5的倍数,符合题意。
选择第四种包装盒正好能把它们装完,因为115是5的倍数。
答:选择第四种包装盒正好能把它们装完,因为115是5的倍数。
21.77平方米
长方形的周长=(长+宽)×2,则长与宽的和为36÷2=18,先列举出18以内的所有质数,再找出和为18的质数,最后根据“长方形的面积=长×宽”求出这块长方形地的最大面积,据此解答。
36÷2=18(米)
18以内的质数有2、3、5、7、11、13、17。
5+13=18(米)
7+11=18(米)
5×13=65(平方米)
7×11=77(平方米)
答:这块长方形地的面积最大是77平方米。
22.(1)510平方分米
(2)450升
(1)根据题意,给长方体水池的四周及底部贴上瓷砖,即贴瓷砖的是长方体的下面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是需要贴瓷砖的面积。
(2)如果要往这个水池里注入5分米深的水,根据长方体的体积=长×宽×高,求出水的体积,然后根据进率“1立方分米=1升”换算单位即可。
(1)15×6+15×10×2+6×10×2
=90+300+120
=510(平方分米)
答:需要贴瓷砖的面积是510平方分米。
(2)15×6×5
=90×5
=450(立方分米)
450立方分米=450升
答:需要450升水。
23.
用男生人数+女生人数,求出全班人数,再用女生人数÷全部人数,即可解答。
23÷(27+23)
=23÷50
=
答:这个班女生人数占全部人数的。
24.56人
由题意可知,五(2)班的学生人数既是7的倍数,又是4的倍数,并且人数在50到60之间,我们可以通过列举的方式求解,据此解答即可。
4的倍数:4,8,12,16,20,24,28,32,36,40,44,48,52,56,60……
7的倍数:7,14,21,28,35,42,49,56……
所以,4和7的公倍数在50-60之间有:56
答:五(2)班一共有学生56人。
25.(1)都是应用排水法测量实物的体积
(2)1570立方厘米
(1)方法一和方法二都是利用水的体积变化来测量石块的体积。方法一是通过测量放入石块前后水的高度变化,计算出石块的体积;方法二是通过测量溢出的水的体积来直接得到石块的体积。这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法。把石块放入有水的长方体容器中,石块完全浸没在水里(水未溢出),上升部分水的体积就等于石块的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
第②种实验方法。把石块放在盛满水的容器里,石块完全浸没在水里,水溢出来,把溢出来的水倒入圆柱体容器里,溢出的水的体积就等于石块的体积,根据圆柱体的体积公式:V=Sh(S=πr2),把数据代入公式解答。
(1)这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法:
20×15.7×(15-10)
=314×5
=1570(立方厘米)
第②种实验方法:
3.14×52×20
=3.14×25×20
=78.5×20
=1570(立方厘米)
这块石块的体积是1570立方厘米。
(选择其一即可)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中评价试题 2024--2025学年小学数学人教版五年级下册
一、选择题
1.同学们用不同的方式表示自己对的理解,其中正确的有( )。
A.①③ B.②④ C.①②③ D.①③④
2.下面的分数中,不能化成有限小数的是( )。
A. B. C. D.
3.将的分子加上6,要使分数的大小不变,分母应( )。
A.加上6 B.增加2倍 C.加上21 D.扩大到原来的3倍
4.正方体的棱长扩大2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。括号里依次应填入( )。
A.2;8 B.4;8 C.6;8 D.8;4
5.一个棱长是30cm的正方体盒子里面装了一些水,水深20cm,将一块石头完全浸入水中,水面上升了4cm,这块石头的体积是( )cm3。
A.1600 B.2400 C.3600 D.18000
二、填空题
6.51的因数有( ),在这些因数中既是奇数又是质数的有( )。
7.3900平方厘米=( )平方米 5立方米6立方分米=( )立方米
8.同时是2、3、5的倍数的最大两位数是( ),同时有因数2、3、5的最小三位数是( )。
9.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
10.把7米长的铁丝平均截成9段,每段长( )米,每段是全长的( )。
11.
12.把一个长60cm,宽40cm,高30cm的长方体木块削成一个体积最大的正方体,削去部分的体积是( )cm3。
13.一个立体图形,从上面看到的图形是,从前面看到的图形是,摆这个立体图形至少需要( )个正方体小块。
14.把2个棱长为3cm的正方体拼成一个长方体,这个长方体的表面积是( )cm2,体积是( )cm3。
三、计算题
15.直接写出得数。
63= 6×3= 6+6+6= 2.3×1.9=
0.5×0.5= 6.7×0.25= 5.13÷3= 29÷18=
16.简算下面各题。
857×1.9-8.57×80-85.7 12.5×32×2.5
17.求下列图形的表面积和体积。
四、作图题
18.请在括号里写出一个分数,并在图中涂一涂表示出来。
( ) ( ) ( )
19.在方格纸上画出正方体的展开图。(每格代表1厘米)
五、解答题
20.我市某购物中心商品齐全,服务周到,吸引了大量顾客。该购物中心的甜品店制作了115个面包,选择哪种包装盒正好能把它们装完?为什么?
21.为了上好劳动课,学校在教学楼后面划出一块长方形地作为劳动实践基地——植物种植角,这块长方形地的长和宽都是质数,周长是36米,这块长方形地的面积最大是多少呢?(要写出推导过程)
22.一个长方体水池从里面量长15分米,宽6分米,高10分米。
(1)如果把这个水池的四周及底部贴上瓷砖,那么需要贴瓷砖的面积是多少?
(2)如果要往这个水池里注入5分米深的水,那么需要多少升水?
23.解放路小学五(1)班共有男生27人,女生23人,这个班女生占全班人数的几分之几?
24.五(2)班人数在50到60之间,上体育课时,每7名学生一排或每4名学生一排都正好排完没有剩余。五(2)班一共有学生多少人?
25.亮亮利用两种方法测量一块石块的体积。(单位:厘米)
方法一 方法二
(1)这两种方法相同的地方是 。
(2)请选择你喜欢的一种方法计算这块石块的体积。
参考答案
1.D
分数的意义:把一个物体或一些物体看作一个整体,即单位“1”,平均分成若干份,表示其中的1份或几份的数,分母表示分成的份数,分子表示取出的份数;分数与除法的关系:被除数相当于分子,除号相当于分数线,除数相当于分母,据此解答。
①5÷4=
白纸条是4份,灰纸条是5份,即灰纸条的长度正好是白纸条的;
②4÷5=
线段的总长度是4,平均分成5份,其中的1段是;
③5÷4=(张)
把5张饼看作一个整体,即单位“1”;平均分成4份,每人分得张;
④5÷4=
把1看作单位“1”,平均分成4份,其中的5份表示。
正确的是①③④,共3个。
故答案为:D
2.D
分数化成小数:用分子去除分母,能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位数。
=3÷5=0.6
=7÷32=0.21875
=21÷35=0.6
=5÷12=0.4166…
因此不能化成有限小数的是。
故答案为:D
3.D
根据分数的基本性质,分子和分母同时乘或除以相同的数(0除外),分数的大小不变;将的分子加上6,分子由原来的3变成(3+6=9),相当于分子乘3,结合各选项的内容,逐项进行分析,据此解答。
A.分母加上6,现在的分数为,分数的大小发生改变,不符合题意;
B.分母增加2倍,现在的分数为,分数的大小发生改变,不符合题意;
C.分母加上21,现在的分数为,分数的大小发生改变,不符合题意;
D.分母扩大到原来的3倍,现在的分数为,分数的大小不变,符合题意。
故答案为:D
4.B
根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长可知,正方体的棱长扩大2倍,表面积扩大到原来的(2×2)倍,体积扩大到原来的(2×2×2)倍,据此解答。
2×2=4
2×2×2=8
正方体的棱长扩大2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:B
5.C
由题意可知,上升的水的体积等于这块石头的体积,上升的水的体积可以看成长是30cm,宽是30cm,高是4cm的长方体的体积,根据,代入数据计算即可。
(cm3)
一个棱长是30cm的正方体盒子里面装了一些水,水深20cm,将一块石头完全浸入水中,水面上升了4cm,这块石头的体积是3600cm3。
故答案为:C
6. 1、3、17、51 3、17
求一个数的因数时,就用这个数从1开始去整除,一直除到除数和商交换位置或除数和商相同为止,除数和商都是被除数的因数,重复的因数只写一个;整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数;一个数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,1既不是质数也不是合数;先列举出51的所有因数,再从里面找出既是奇数又是质数的数,据此解答。
51÷1=51
51÷3=17
所以,51的因数有1、3、17、51,在这些因数中既是奇数又是质数的有3、17。
7. 0.39 5.006
1平方米=10000平方厘米 1立方米=1000立方分米
高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率。据此解答。
1平方米=10000平方厘米 3900÷10000=0.39 3900平方厘米=0.39平方米
1立方米=1000立方分米 6÷1000=0.006 5立方米6立方分米=5.006立方米
8. 90 120
2,3,5的倍数的特征:个位上的数字是0,各个数位上的数字的和是3的倍数的数。
同时是2、3、5的倍数的最大两位数是90,同时有因数2、3、5的最小三位数是120。
9. ② ③
观察图形,再添加一个同样的小方块,从左面看到的图形不变,说明从左面看不到某位置上新放的小方块,据此得出添加的小方块放在②号位置上;
再添加一个同样的小方块,从前面看到的图形不变,说明从前面看不到某位置上新放的小方块,据此得出添加的小方块应放在③号位置上。
如图:
在②号位置上面放一个同样的小方块,从左面看:
在③号位置上面放一个同样的小方块,从前面看:
填空如下:
在 ② 号位置上面放一个同样的小方块,从左面看到的图形不变,在 ③ 号位置上面放一个同样的小方块,从前面看到的图形不变。
10.
求每段长多少米,用铁丝的长度÷平均截的段数;把铁丝的全长看作单位“1”,平均分成9段,求每段是全长的几分之几,用1÷9解答。
7÷9=(米)
1÷9=
把7米长的铁丝平均截成9段,每段长米,每段是全长的。
11.2;12;10;6
(1)的分子和分母同时除以3求出分子,根据分数与除法的关系把转化为除法,再利用商不变的规律求出除数;
(2)根据分数与除法的关系把2÷5转化为分数,再利用“分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变”求出分母和分子,据此解答。
(1)
=2÷3=(2×4)÷(3×4)=8÷12
所以,==8÷12。
(2)2÷5=
所以,==2÷5。
12.45000
分析题目,削成的最大的正方体的棱长等于长方体的最短边即30cm,削去部分的体积等于长方体的体积减去正方体的体积,据此结合长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长代入数据列式计算即可。
60×40×30-30×30×30
=2400×30-900×30
=72000-27000
=45000(cm3)
把一个长60cm,宽40cm,高30cm的长方体木块削成一个体积最大的正方体,削去部分的体积是45000cm3。
13.11
根据从上面看到的图形可知,这个立体图形底下一层有9个正方体小块。再根据从前面看到的图形可知,上面一层至少有2个正方体小块。据此解题。
9+2=11(个)
所以,摆这个立体图形至少需要11个正方体小块。
14. 90 54
由题意可知,拼成的长方体的长是cm,宽是3cm,高是3cm,根据、,代入数据计算即可得解。
(cm2)
(cm3)
把2个棱长为3cm的正方体拼成一个长方体,这个长方体的表面积是90cm2,体积是54cm3。
15.216;18;18;4.37;
0.25;1.675;1.71;
略
16.857;9;1000
第一题将857×1.9写成8.57×190,把85.7写成8.57×10,再利用乘法分配律进行简便计算即可;
第二题利用加法交换律、结合律及减法的性质进行简便计算即可;
第三题先将32写成8×4,再利用结合律分别计算12.5×8和4×2.5,最后把这两个结果相乘即可。
857×1.9-8.57×80-85.7
=8.57×190-8.57×80-8.57×10
=8.57×(190-80-10)
=8.57×100
=857
=(6.75+3.25)-()
=10-1
=9
12.5×32×2.5
=12.5×8×4×2.5
=(12.5×8)×(4×2.5)
=100×10
=1000
17.表面积470cm2;体积600cm3
表面积384cm2;体积512cm3
(1)图形是一个长为8cm,宽为5cm,高为15cm的长方体,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入相应数值计算;
(2)图形是一个棱长为8cm的正方体,根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入相应数值计算。
表面积:(8×5+8×15+5×15)×2
=(40+120+75)×2
=235×2
=470(cm2)
体积:8×5×15
=40×15
=600(cm3)
图形的表面积是470cm2,体积是600cm3。
表面积:8×8×6
=64×6
=384(cm2)
体积:8×8×8
=64×8
=512(cm3)
图形的表面积是384cm2,体积是512cm3。
18.见详解
先写合适的分数,再根据分数的意义涂色即可;
表示把8个圆圈看作一个整体,平均分成8份,取其中的7份涂色;
表示把大三角形看作一个整体,平均分成4份,取其中的1份涂色;
表示把圆看作一个整体,平均分成4份,取其中的3份涂色;
据此解答即可。
(答案不唯一)
19.见详解
正方体表面展开图有11种情况画出一种即可。
1-4-1型 (6种):中间一行有4个正方形,上下各接1个正方形。通过调整上下两个正方形的位置,形成6种不同的图形。
2-3-1型 (3种):第一行有2个正方形,中间一行有3个,最后一行有1个,通过不同连接方式产生3种图形。
3-3型 (1种):上下两行各3个正方形,呈阶梯状排列。
2-2-2型 (1种):三行各2个正方形,呈“Z”字形排列。
由分析可作图11种:
将其中一种画在方格纸上
(答案不唯一)
20.选择第四种包装盒正好能把它们装完;因为115是5的倍数
面包的总个数是每个包装盒装面包的个数的倍数,就选择哪种包装盒,据此解答。
第一种:115÷2=57(盒)……1(个),115不是2的倍数,不符合题意。
第二种:115÷3=38(盒)……1(个),115不是3的倍数,不符合题意。
第三种:115÷4=28(盒)……3(个),115不是4的倍数,不符合题意。
第四种:115÷5=23(盒),115是5的倍数,符合题意。
选择第四种包装盒正好能把它们装完,因为115是5的倍数。
答:选择第四种包装盒正好能把它们装完,因为115是5的倍数。
21.77平方米
长方形的周长=(长+宽)×2,则长与宽的和为36÷2=18,先列举出18以内的所有质数,再找出和为18的质数,最后根据“长方形的面积=长×宽”求出这块长方形地的最大面积,据此解答。
36÷2=18(米)
18以内的质数有2、3、5、7、11、13、17。
5+13=18(米)
7+11=18(米)
5×13=65(平方米)
7×11=77(平方米)
答:这块长方形地的面积最大是77平方米。
22.(1)510平方分米
(2)450升
(1)根据题意,给长方体水池的四周及底部贴上瓷砖,即贴瓷砖的是长方体的下面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是需要贴瓷砖的面积。
(2)如果要往这个水池里注入5分米深的水,根据长方体的体积=长×宽×高,求出水的体积,然后根据进率“1立方分米=1升”换算单位即可。
(1)15×6+15×10×2+6×10×2
=90+300+120
=510(平方分米)
答:需要贴瓷砖的面积是510平方分米。
(2)15×6×5
=90×5
=450(立方分米)
450立方分米=450升
答:需要450升水。
23.
用男生人数+女生人数,求出全班人数,再用女生人数÷全部人数,即可解答。
23÷(27+23)
=23÷50
=
答:这个班女生人数占全部人数的。
24.56人
由题意可知,五(2)班的学生人数既是7的倍数,又是4的倍数,并且人数在50到60之间,我们可以通过列举的方式求解,据此解答即可。
4的倍数:4,8,12,16,20,24,28,32,36,40,44,48,52,56,60……
7的倍数:7,14,21,28,35,42,49,56……
所以,4和7的公倍数在50-60之间有:56
答:五(2)班一共有学生56人。
25.(1)都是应用排水法测量实物的体积
(2)1570立方厘米
(1)方法一和方法二都是利用水的体积变化来测量石块的体积。方法一是通过测量放入石块前后水的高度变化,计算出石块的体积;方法二是通过测量溢出的水的体积来直接得到石块的体积。这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法。把石块放入有水的长方体容器中,石块完全浸没在水里(水未溢出),上升部分水的体积就等于石块的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
第②种实验方法。把石块放在盛满水的容器里,石块完全浸没在水里,水溢出来,把溢出来的水倒入圆柱体容器里,溢出的水的体积就等于石块的体积,根据圆柱体的体积公式:V=Sh(S=πr2),把数据代入公式解答。
(1)这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法:
20×15.7×(15-10)
=314×5
=1570(立方厘米)
第②种实验方法:
3.14×52×20
=3.14×25×20
=78.5×20
=1570(立方厘米)
这块石块的体积是1570立方厘米。
(选择其一即可)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
