27.2.1相似三角形的判定(1)
文档属性
| 名称 | 27.2.1相似三角形的判定(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-30 00:00:00 | ||
图片预览


文档简介
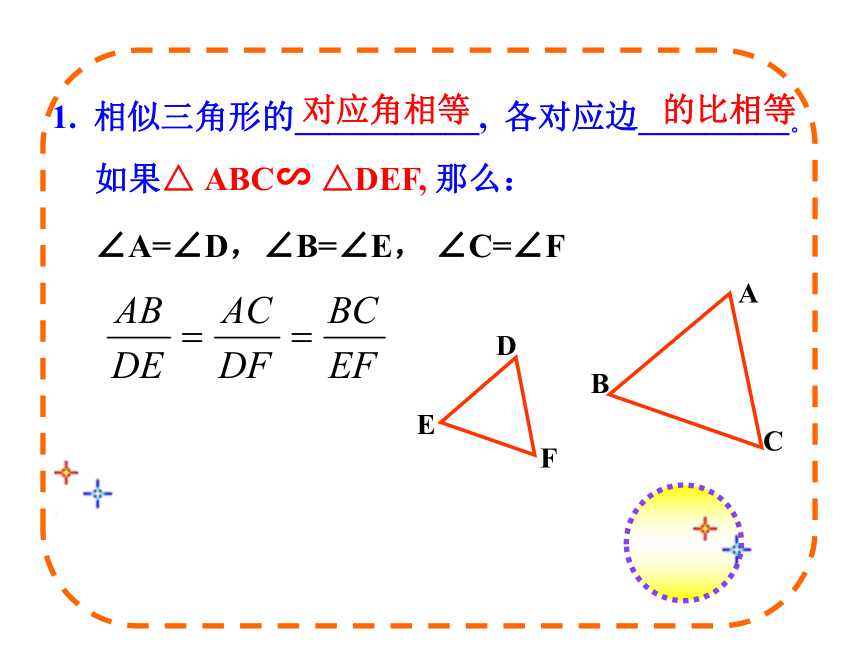
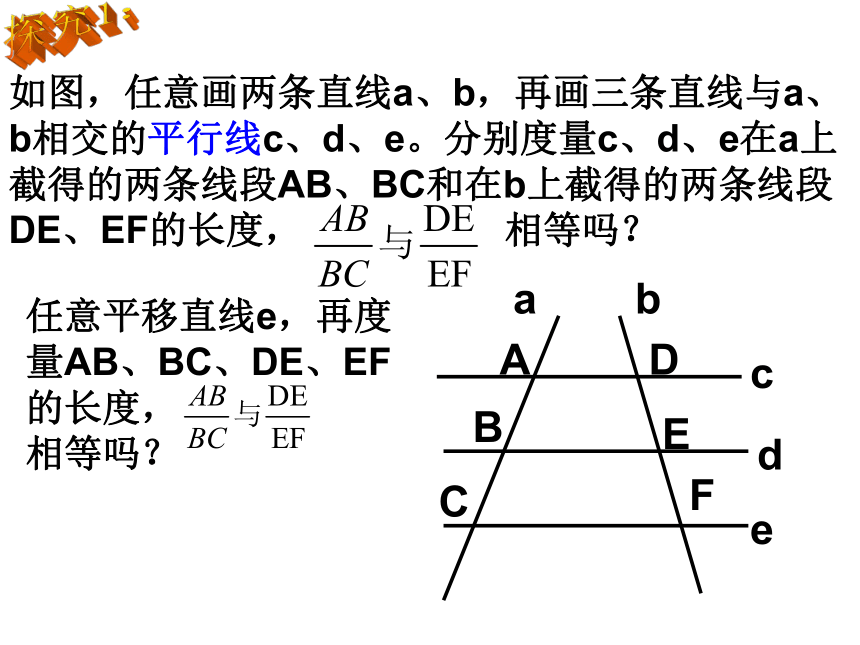
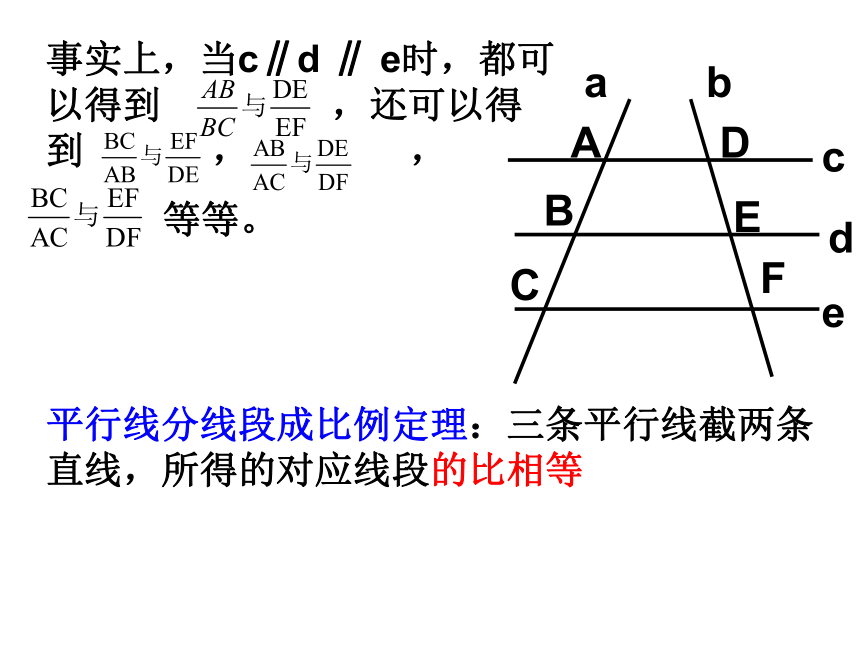
课件20张PPT。27.2.1相似三角形的判定(一)1. 相似三角形的___________, 各对应边_________。对应角相等的比相等如果△ ABC∽ △DEF, 那么:∠A=∠D,∠B=∠E, ∠C=∠F回顾当两个三角形的相似比为1时,它们是全等的,全等是相似的一种特殊情况。 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.2、相似三角形的判定相似三角形与全等三角形有什么内在的联系呢?= k∴△ABC △A′B′C′∵∽探究1:如图,任意画两条直线a、b,再画三条直线与a、b相交的平行线c、d、e。分别度量c、d、e在a上截得的两条线段AB、BC和在b上截得的两条线段DE、EF的长度, 相等吗?任意平移直线e,再度量AB、BC、DE、EF的长度, 相等吗?平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段的比相等事实上,当c∥d ∥ e时,都可以得到 ,还可以得到 , ,
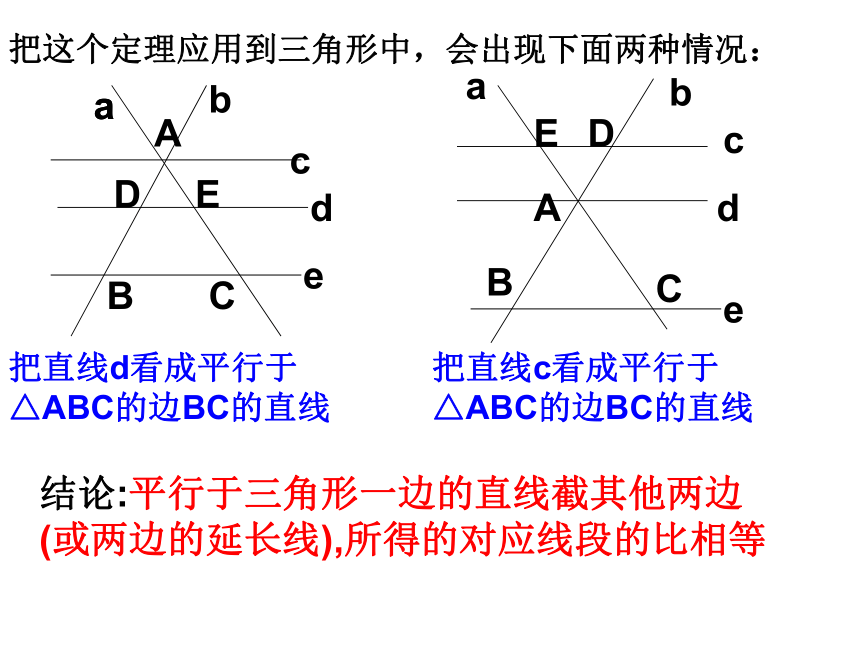
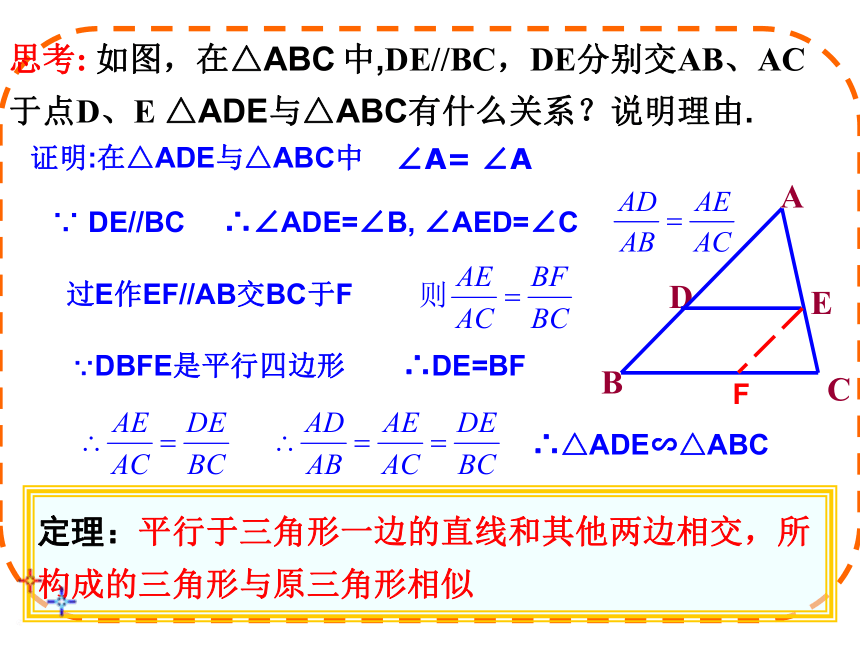
等等。把这个定理应用到三角形中,会出现下面两种情况:把直线d看成平行于△ABC的边BC的直线把直线c看成平行于△ABC的边BC的直线结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等思考: 如图,在△ABC 中,DE//BC,DE分别交AB、AC于点D、E △ADE与△ABC有什么关系?说明理由.ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵DBFE是平行四边形F∴DE=BF定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∴△ADE∽△ABC平行于三角形一边的直线和其他两边(或其延长线)相交,所构成的三角形与原三角形相似符号表达:∵DE∥BC ∴⊿ABC∽⊿ADE
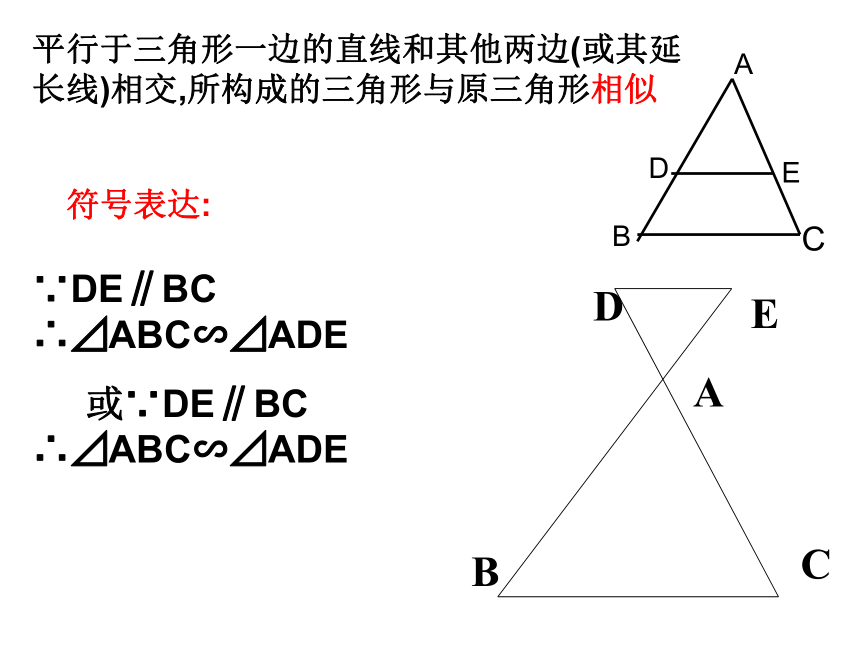
或∵DE∥BC ∴⊿ABC∽⊿ADEABCDEAEDCB 平行于三角形一边的直线与其它两边(或
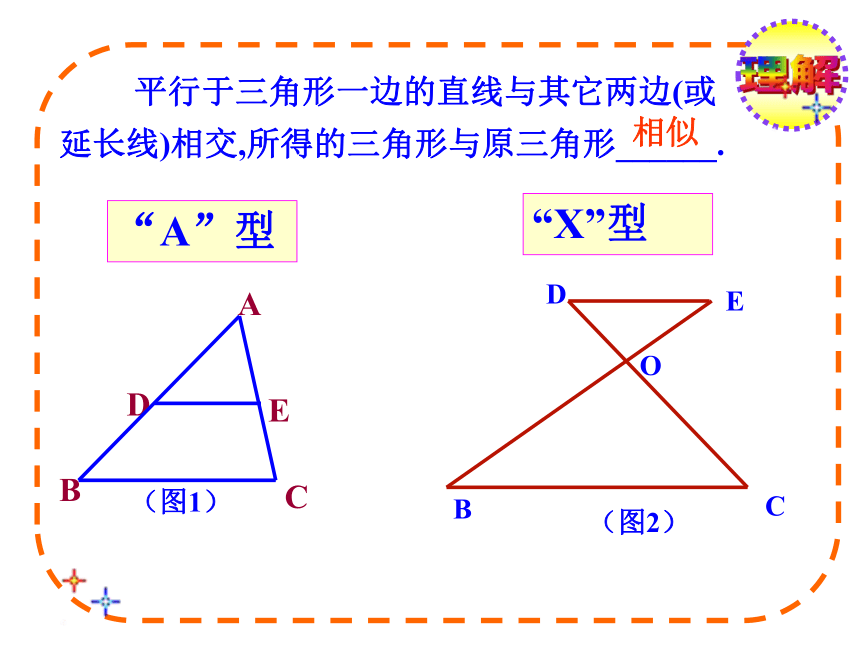
延长线)相交,所得的三角形与原三角形______.相似“A”型 “X”型 理解 已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解 如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE运用4如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4运用课堂练习: 已知四边形ABCD为平行四边形,请找出所有的相似三角形例题例1:如图△ABC∽△ACD,AB:AC=5:2 ,AD=2cm,DC=6cm,求AC和BC的长ABCD例题例2:如图,在平行四边形ABCD中,过点A的直线交对角线BD于E,交BC于F,交DC的延长线于G,求证:AE2=EF . EGABCDEFG例题例3:如图,在△ABC中,AD是角平分线,求证:
AB:AC=BD:DCABCD例4.在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,
然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)BACDE练习:1.如图:DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比是( )
2.如图.E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于F,则图中共有相似三角形几对?
ABCDEFABCDE练习:3.如图,在平行四边形ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE.BD交于点F,则BF:FD=( )
4.如图,在△ABC中, ∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,AC=6,求BC的长AABBCCDDEEFwww.czsx.com.cn结束寄语不经历风雨,怎么见彩虹.,没有人能随随便便成功!
等等。把这个定理应用到三角形中,会出现下面两种情况:把直线d看成平行于△ABC的边BC的直线把直线c看成平行于△ABC的边BC的直线结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等思考: 如图,在△ABC 中,DE//BC,DE分别交AB、AC于点D、E △ADE与△ABC有什么关系?说明理由.ABCDE证明:在△ADE与△ABC中∠A= ∠A∵ DE//BC∴∠ADE=∠B, ∠AED=∠C过E作EF//AB交BC于F∵DBFE是平行四边形F∴DE=BF定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∴△ADE∽△ABC平行于三角形一边的直线和其他两边(或其延长线)相交,所构成的三角形与原三角形相似符号表达:∵DE∥BC ∴⊿ABC∽⊿ADE
或∵DE∥BC ∴⊿ABC∽⊿ADEABCDEAEDCB 平行于三角形一边的直线与其它两边(或
延长线)相交,所得的三角形与原三角形______.相似“A”型 “X”型 理解 已知:如图,AB∥EF ∥CD,3图中共有____对相似三角形。 △EOF∽△COD AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC理解 如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE
△GFC
△GOE运用4如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。△ADG∽△AEH∽△AFI∽△ABC1:4运用课堂练习: 已知四边形ABCD为平行四边形,请找出所有的相似三角形例题例1:如图△ABC∽△ACD,AB:AC=5:2 ,AD=2cm,DC=6cm,求AC和BC的长ABCD例题例2:如图,在平行四边形ABCD中,过点A的直线交对角线BD于E,交BC于F,交DC的延长线于G,求证:AE2=EF . EGABCDEFG例题例3:如图,在△ABC中,AD是角平分线,求证:
AB:AC=BD:DCABCD例4.在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,
然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)BACDE练习:1.如图:DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比是( )
2.如图.E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于F,则图中共有相似三角形几对?
ABCDEFABCDE练习:3.如图,在平行四边形ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE.BD交于点F,则BF:FD=( )
4.如图,在△ABC中, ∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,AC=6,求BC的长AABBCCDDEEFwww.czsx.com.cn结束寄语不经历风雨,怎么见彩虹.,没有人能随随便便成功!
