27.2.1三角形相似的判定(2)
文档属性
| 名称 | 27.2.1三角形相似的判定(2) |  | |
| 格式 | rar | ||
| 文件大小 | 799.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-30 12:21:00 | ||
图片预览


文档简介
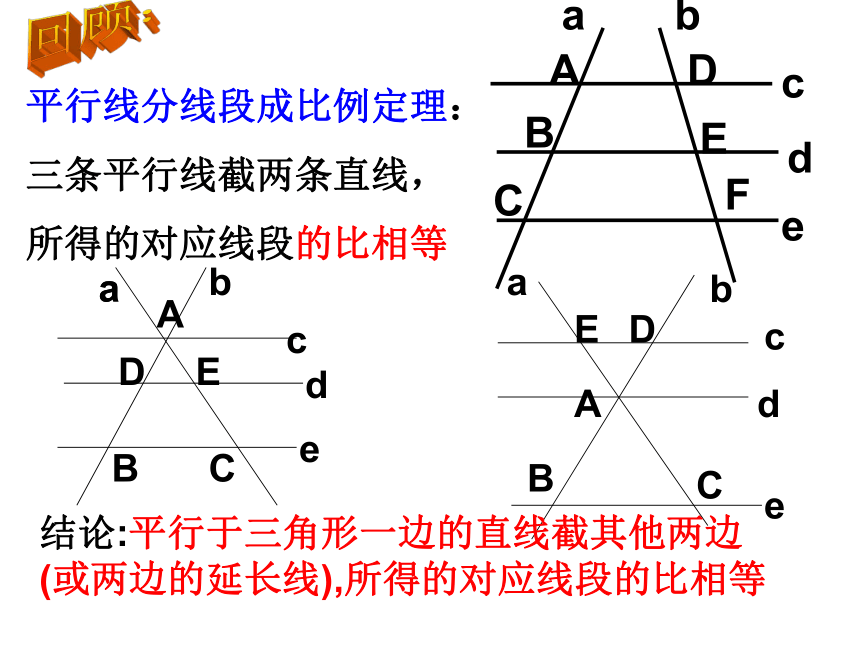
课件22张PPT。27.2.1.2 相似三角形的判定(2)平行线分线段成比例定理:
三条平行线截两条直线,
所得的对应线段的比相等回顾:结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等∵DE∥BC
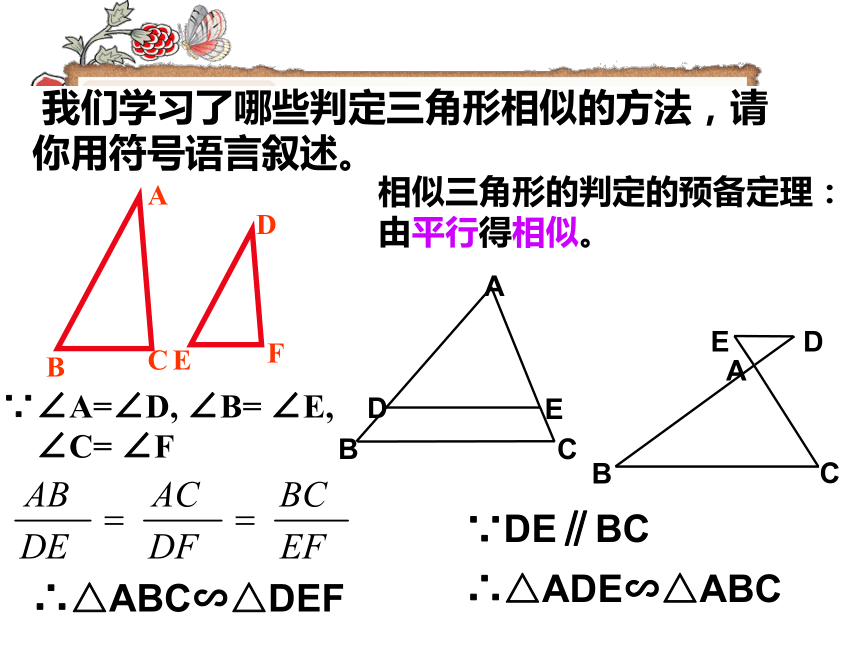
∴△ADE∽△ABC相似三角形的判定的预备定理:
由平行得相似。 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。∵∠A=∠D, ∠B= ∠E,
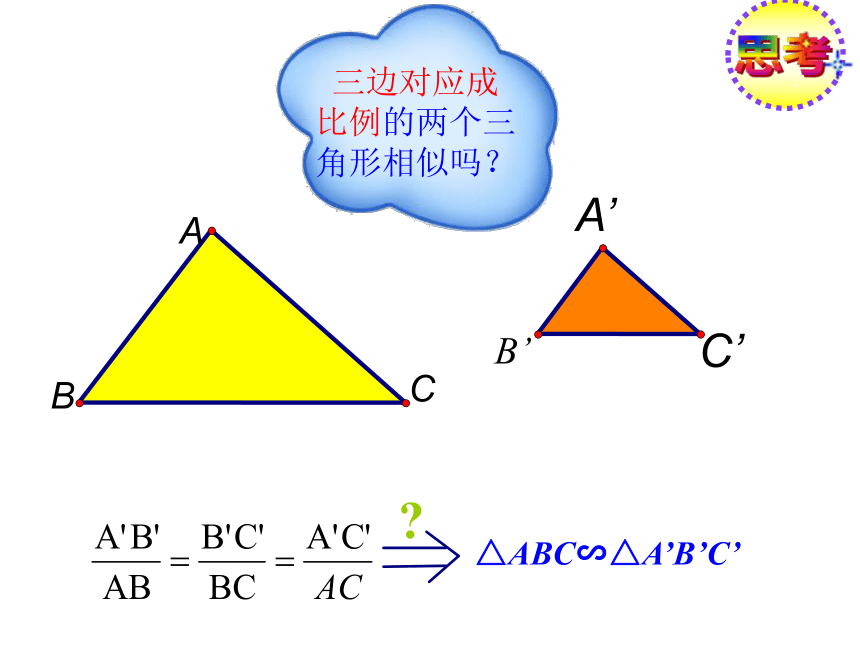
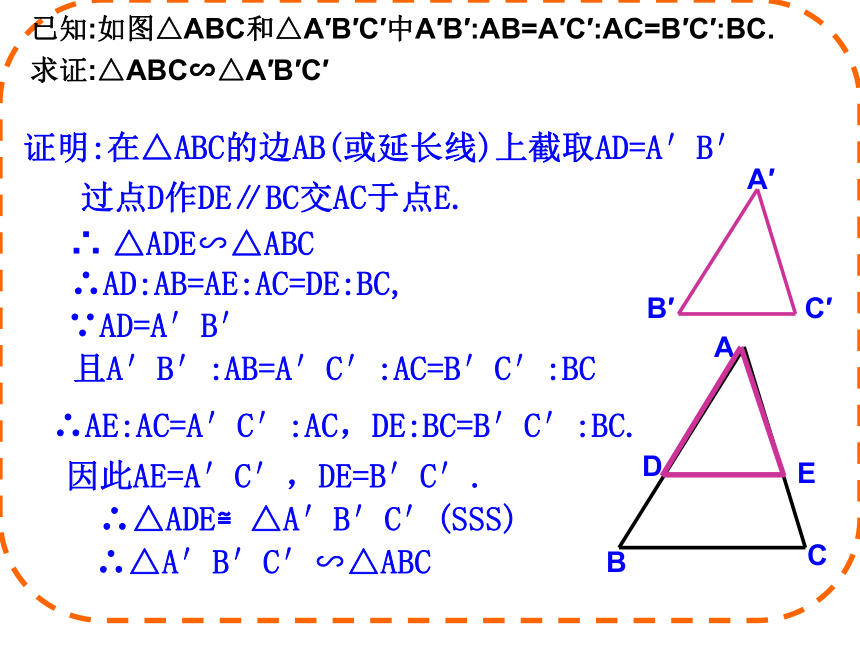
∠C= ∠F∴△ABC∽△DEF思考ABC三边对应成 比例的两个三角形相似吗?△ABC∽△A’B’C’?已知:如图△ABC和△A′B′C′中A′B′:AB=A′C′:AC=B′C′:BC.
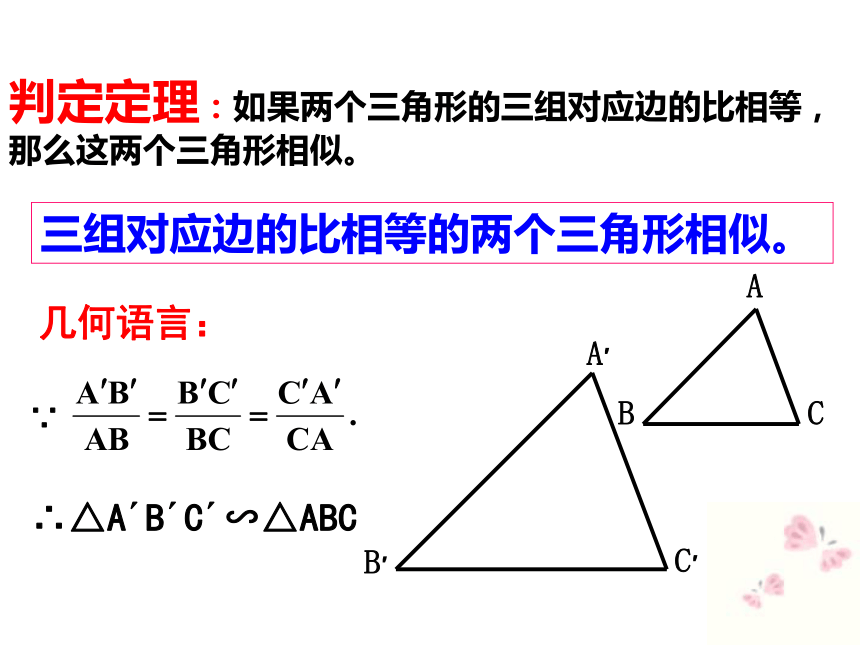
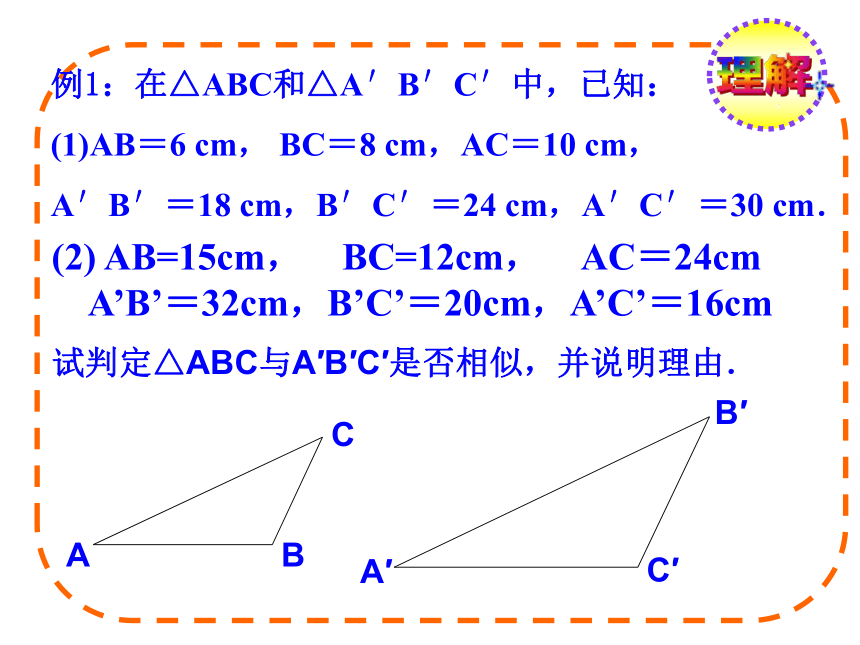
求证:△ABC∽△A′B′C′证明:在△ABC的边AB(或延长线)上截取AD=A′B′ABCDE过点D作DE∥BC交AC于点E.且A′B′:AB=A′C′:AC=B′C′:BC ∴ △ADE∽△ABC ∴AD:AB=AE:AC=DE:BC,∵AD=A′B′∴AE:AC=A′C′:AC,DE:BC=B′C′:BC.因此AE=A′C′,DE=B′C′.∴△A′B′C′∽△ABC ∴△ADE≌△A′B′C′(SSS)判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC∵理解例1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
(2) AB=15cm, BC=12cm, AC=24cm
A’B’=32cm,B’C’=20cm,A’C’=16cm
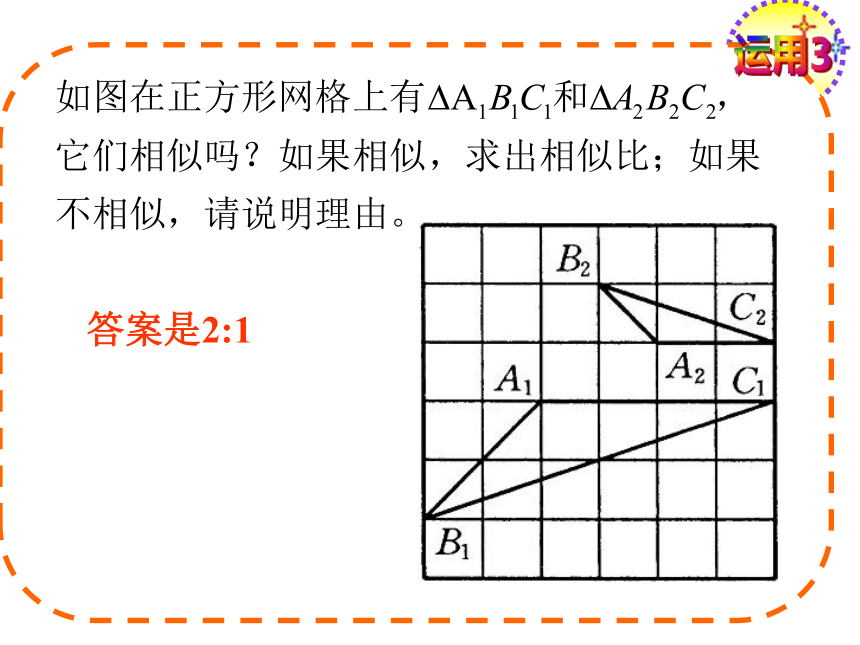
试判定△ABC与A′B′C′是否相似,并说明理由. ABCA′B′C′运用3答案是2:1运用2试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE理解 6:2=4:x=5:y
4:2=5:x=6:y
5:2=4:x=6:y 要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?45622232.41.6 如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC相似呢? 此时, 如果一个三角形的两条边与另一个三角形的两条边对应且比值相等,并且夹角相等,那么这两个三角形一定相似吗? =? 在△ABC和△A′B′C′中,已知:AB∶A′B′
=AC∶A′C′,∠A=∠A′。
求证: △ABC∽△A′B′C′。证明:在A′B′(或它的延长线)上截取
A′D=AB,过点D画DE∥B′C′交
A′C′于点E,
那么: △A′DE∽△A′B′C′
∴A′D∶A′B′=A′E∶A′C′=DE∶B′C′
∴AB∶A′B′=A′E∶A′C′=DE∶B′C′
∵ AB∶A′B′=AC∶A′C′ ∴ AC=A′E
∵∠A=∠A′ AB = A′D ∴△ABC≌△A′DE
∴△ABC∽△A′B′C′ABCA′B′DEC′如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似 。∴△ABC∽△(两边对应成比例且夹角相等的两个三角形相似)A∠A=∠A′思考对于△ABC和△A′B′C′如果
∠B=∠B′,那么这两个三角形一定相似吗?1、已知△ABC和 △A’B’C’,根据下列条件
判断它们是否相似.(2) ∠A=45°,AB=12cm, AC=15cm
∠A′=45°,A′B′=16cm,
A′C′=20cm(1)∠A=120°,AB=7cm,AC=14cm,
∠A′=120°,A′B′=3cm,A′C′=6cm; ∵ = =1.52、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠2 = =1.5∴ =123.在正方形ABCD中,E为AD上的中点, F是AB的四等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.△AEF和EFC呢?4、如图,D、E是△ABC的边AC、AB上的点。
已知:AD·AC=AE·AB
求证:△AED∽△ACB.ABCED 5、已知:如图,A'B ' ∥AB,B ' C ' ∥BC
求证(1) △A ' O C ' ∽△AOC
(2)△A ' B ' C ' ∽△ABC 已知:在直角坐标系中的位置如图所示,P为OB的中点,C点为折线 OAB上的动点,线段PC把△OAB分割成两部分.
问:C点在什么位置时,分割得到的三角形与原△OAB相似?
(注:在图上画出所有符合要求的线段,并求出相应的点的坐标).CC1C2CC1点C的位置是:
(6,6.25)
(6,8)
(3,0)? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.不经历风雨,怎么见彩虹没有人能随随便便成功!再见
三条平行线截两条直线,
所得的对应线段的比相等回顾:结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等∵DE∥BC
∴△ADE∽△ABC相似三角形的判定的预备定理:
由平行得相似。 我们学习了哪些判定三角形相似的方法,请你用符号语言叙述。∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF思考ABC三边对应成 比例的两个三角形相似吗?△ABC∽△A’B’C’?已知:如图△ABC和△A′B′C′中A′B′:AB=A′C′:AC=B′C′:BC.
求证:△ABC∽△A′B′C′证明:在△ABC的边AB(或延长线)上截取AD=A′B′ABCDE过点D作DE∥BC交AC于点E.且A′B′:AB=A′C′:AC=B′C′:BC ∴ △ADE∽△ABC ∴AD:AB=AE:AC=DE:BC,∵AD=A′B′∴AE:AC=A′C′:AC,DE:BC=B′C′:BC.因此AE=A′C′,DE=B′C′.∴△A′B′C′∽△ABC ∴△ADE≌△A′B′C′(SSS)判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC∵理解例1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
(2) AB=15cm, BC=12cm, AC=24cm
A’B’=32cm,B’C’=20cm,A’C’=16cm
试判定△ABC与A′B′C′是否相似,并说明理由. ABCA′B′C′运用3答案是2:1运用2试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE理解 6:2=4:x=5:y
4:2=5:x=6:y
5:2=4:x=6:y 要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?45622232.41.6 如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC相似呢? 此时, 如果一个三角形的两条边与另一个三角形的两条边对应且比值相等,并且夹角相等,那么这两个三角形一定相似吗? =? 在△ABC和△A′B′C′中,已知:AB∶A′B′
=AC∶A′C′,∠A=∠A′。
求证: △ABC∽△A′B′C′。证明:在A′B′(或它的延长线)上截取
A′D=AB,过点D画DE∥B′C′交
A′C′于点E,
那么: △A′DE∽△A′B′C′
∴A′D∶A′B′=A′E∶A′C′=DE∶B′C′
∴AB∶A′B′=A′E∶A′C′=DE∶B′C′
∵ AB∶A′B′=AC∶A′C′ ∴ AC=A′E
∵∠A=∠A′ AB = A′D ∴△ABC≌△A′DE
∴△ABC∽△A′B′C′ABCA′B′DEC′如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似 。∴△ABC∽△(两边对应成比例且夹角相等的两个三角形相似)A∠A=∠A′思考对于△ABC和△A′B′C′如果
∠B=∠B′,那么这两个三角形一定相似吗?1、已知△ABC和 △A’B’C’,根据下列条件
判断它们是否相似.(2) ∠A=45°,AB=12cm, AC=15cm
∠A′=45°,A′B′=16cm,
A′C′=20cm(1)∠A=120°,AB=7cm,AC=14cm,
∠A′=120°,A′B′=3cm,A′C′=6cm; ∵ = =1.52、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠2 = =1.5∴ =123.在正方形ABCD中,E为AD上的中点, F是AB的四等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.△AEF和EFC呢?4、如图,D、E是△ABC的边AC、AB上的点。
已知:AD·AC=AE·AB
求证:△AED∽△ACB.ABCED 5、已知:如图,A'B ' ∥AB,B ' C ' ∥BC
求证(1) △A ' O C ' ∽△AOC
(2)△A ' B ' C ' ∽△ABC 已知:在直角坐标系中的位置如图所示,P为OB的中点,C点为折线 OAB上的动点,线段PC把△OAB分割成两部分.
问:C点在什么位置时,分割得到的三角形与原△OAB相似?
(注:在图上画出所有符合要求的线段,并求出相应的点的坐标).CC1C2CC1点C的位置是:
(6,6.25)
(6,8)
(3,0)? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.不经历风雨,怎么见彩虹没有人能随随便便成功!再见
