三角形的相似判定(3)
图片预览

文档简介
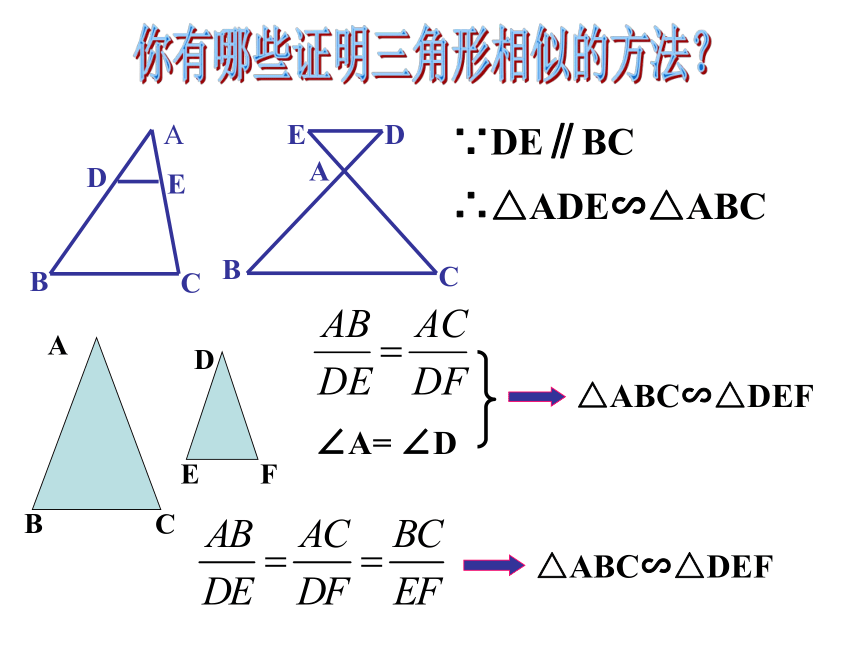
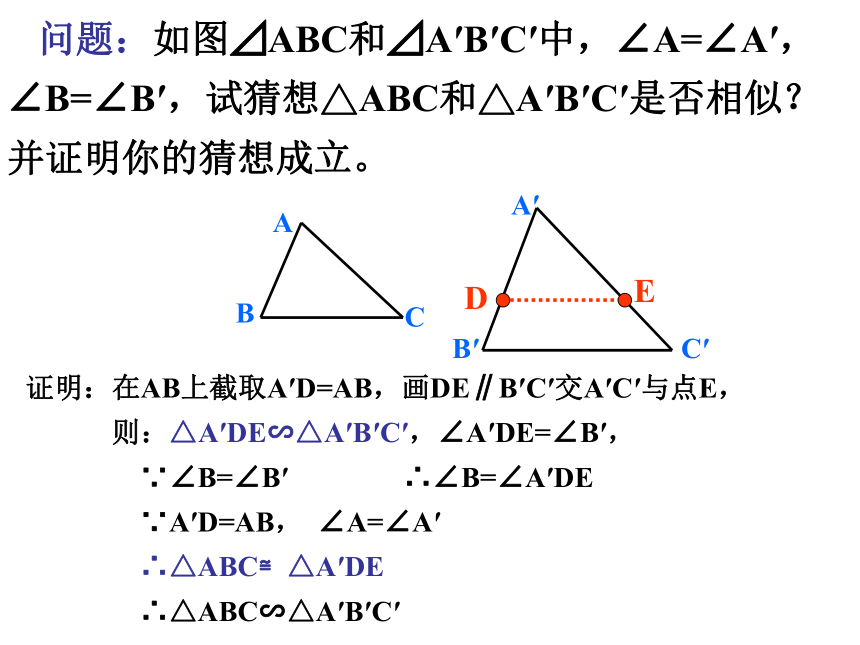
课件13张PPT。27.2.1 相似三角形的判定(3)∵DE∥BC ∴△ADE∽△ABC∠A= ∠D△ABC∽△DEF△ABC∽△DEF你有哪些证明三角形相似的方法? 问题:如图⊿ABC和⊿A′B′C′中,∠A=∠A′,∠B=∠B′,试猜想△ABC和△A′B′C′是否相似?并证明你的猜想成立。BACA′B′C′DE证明:在AB上截取A′D=AB,画DE∥B′C′交A′C′与点E,
则:△A′DE∽△A′B′C′,∠A′DE=∠B′,
∵∠B=∠B′ ∴∠B=∠A′DE
∵A′D=AB, ∠A=∠A′
∴△ABC≌△A′DE
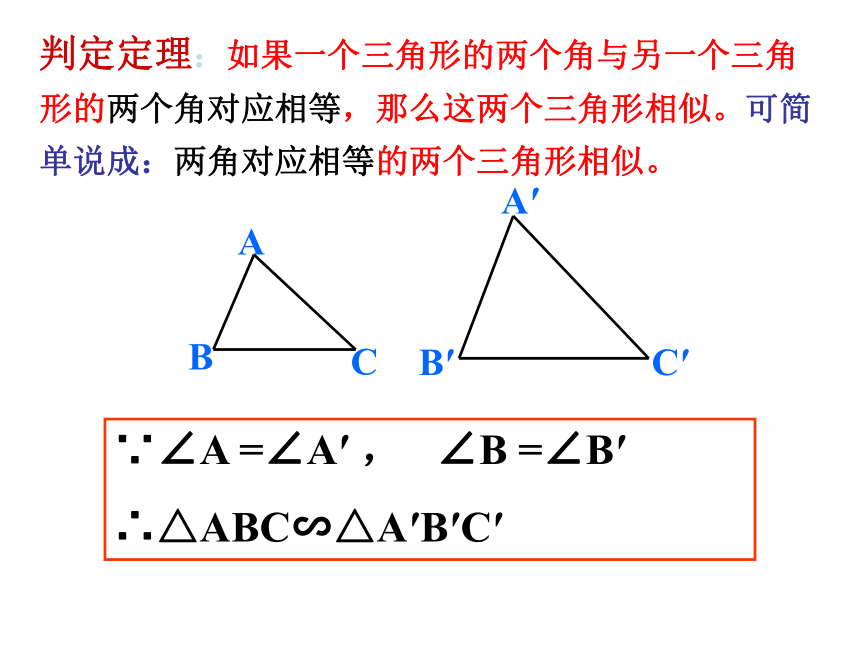
∴△ABC∽△A′B′C′判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可简单说成:两角对应相等的两个三角形相似。∵∠A =∠A′ , ∠B =∠B′
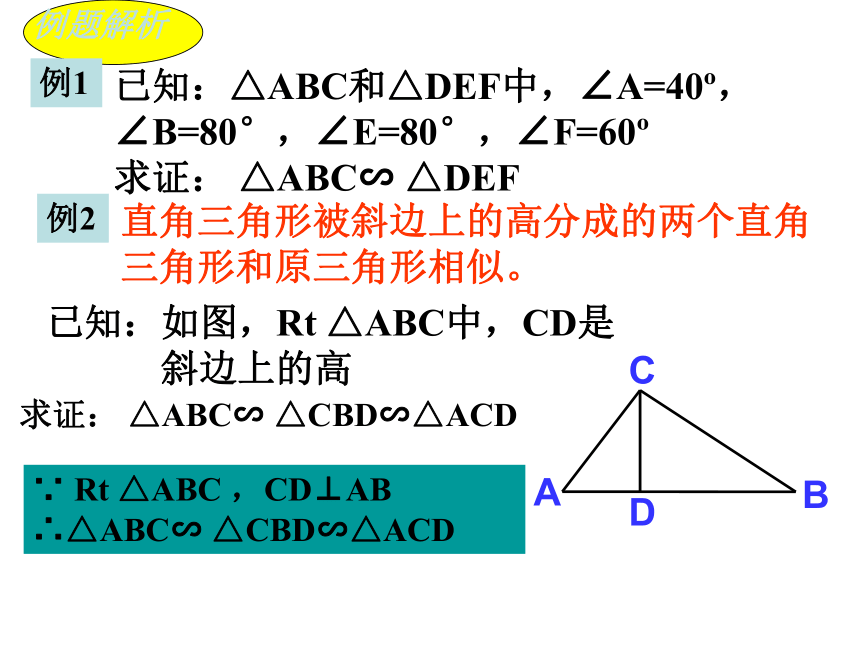
∴△ABC∽△A′B′C′例1已知:△ABC和△DEF中,∠A=40o,∠B=80°,∠E=80°,∠F=60o
求证: △ABC∽ △DEF例2直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:如图,Rt △ABC中,CD是
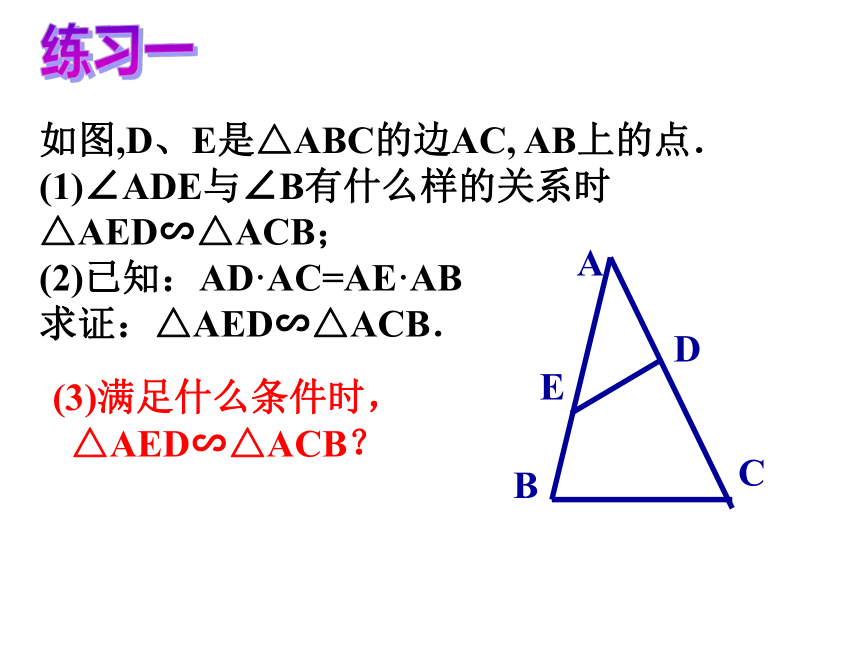
斜边上的高求证: △ABC∽ △CBD∽△ACD∵ Rt △ABC ,CD⊥AB ∴△ABC∽ △CBD∽△ACD如图,D、E是△ABC的边AC, AB上的点.
(1)∠ADE与∠B有什么样的关系时△AED∽△ACB;
(2)已知:AD·AC=AE·AB
求证:△AED∽△ACB.
练习一(3)满足什么条件时,
△AED∽△ACB?
3、已知:如图,A、B、C、D是在同一圆上,弦AB、DC相交于点P。
求证: (1)PA·PB=PC·PD;(2)∠PCB =∠PAD。PADCB12 若AB与CD相交于圆内一
点P,结论(1)成立吗?根据下列条件,判定Rt△ABC和Rt△A′B′C′
是否相似,其中∠C=∠C′=90 °(2)AC=14cm,BC=6cm,
A′B′=7cm,B′C′=3cm(1)∠A=63°∠B’=27°(3)AC= ,BC= ,
A′B′= ,B′C′= 提问1:有一个锐角相等的两个直角三角形是否相似?提问2:一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似? 提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢? 1.如图,CE交△ABC的高线AD于点O,交AB于E,且OC·BD=AB·OD,求证:CE⊥AB. 2 .如图, ∠DEB= ∠ACB=Rt ∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC。 如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?我们来试一试…ACB.P相似三角形的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。再见
则:△A′DE∽△A′B′C′,∠A′DE=∠B′,
∵∠B=∠B′ ∴∠B=∠A′DE
∵A′D=AB, ∠A=∠A′
∴△ABC≌△A′DE
∴△ABC∽△A′B′C′判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可简单说成:两角对应相等的两个三角形相似。∵∠A =∠A′ , ∠B =∠B′
∴△ABC∽△A′B′C′例1已知:△ABC和△DEF中,∠A=40o,∠B=80°,∠E=80°,∠F=60o
求证: △ABC∽ △DEF例2直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:如图,Rt △ABC中,CD是
斜边上的高求证: △ABC∽ △CBD∽△ACD∵ Rt △ABC ,CD⊥AB ∴△ABC∽ △CBD∽△ACD如图,D、E是△ABC的边AC, AB上的点.
(1)∠ADE与∠B有什么样的关系时△AED∽△ACB;
(2)已知:AD·AC=AE·AB
求证:△AED∽△ACB.
练习一(3)满足什么条件时,
△AED∽△ACB?
3、已知:如图,A、B、C、D是在同一圆上,弦AB、DC相交于点P。
求证: (1)PA·PB=PC·PD;(2)∠PCB =∠PAD。PADCB12 若AB与CD相交于圆内一
点P,结论(1)成立吗?根据下列条件,判定Rt△ABC和Rt△A′B′C′
是否相似,其中∠C=∠C′=90 °(2)AC=14cm,BC=6cm,
A′B′=7cm,B′C′=3cm(1)∠A=63°∠B’=27°(3)AC= ,BC= ,
A′B′= ,B′C′= 提问1:有一个锐角相等的两个直角三角形是否相似?提问2:一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似? 提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢? 1.如图,CE交△ABC的高线AD于点O,交AB于E,且OC·BD=AB·OD,求证:CE⊥AB. 2 .如图, ∠DEB= ∠ACB=Rt ∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC。 如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?我们来试一试…ACB.P相似三角形的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。再见
