24.4 解直角三角形(第一课时) 课件(共26张PPT) 华东师大(2012)九年级上册
文档属性
| 名称 | 24.4 解直角三角形(第一课时) 课件(共26张PPT) 华东师大(2012)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 07:55:13 | ||
图片预览







文档简介
(共26张PPT)
24.4 解直角三角形
(第一课时)
学习目标
1. 会运用直角三角形的两个锐角互余及锐角三角函数解直角三角形(重点)
2. 能够把实际问题转化成解直角三角形的问题(难点)
新课导入
我们前面学习了直角三角形的有关性质以及边角之间的各种关系,这些性质在我们生活中有什么作用吗?在我们生活中有什么应用吗?
这节课我们将学习直角三角形在生活中的应用.
新课学习
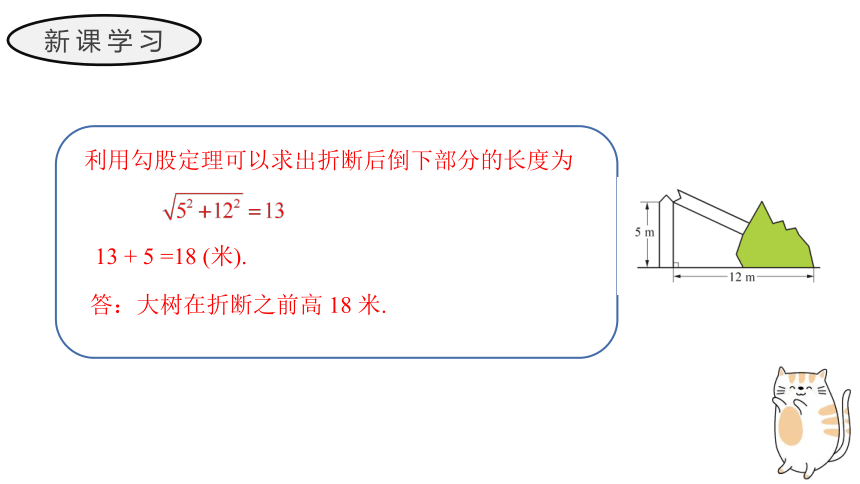
例1:如图,一棵大树在一次强烈的地震中于离地面5 米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少?
新课学习
利用勾股定理可以求出折断后倒下部分的长度为
13 + 5 =18 (米).
答:大树在折断之前高 18 米.
新课学习
解直角三角形的概念
在直角三角形中,由已知的元素求出未知元素的过程,叫做解直角三角形.
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
新课学习
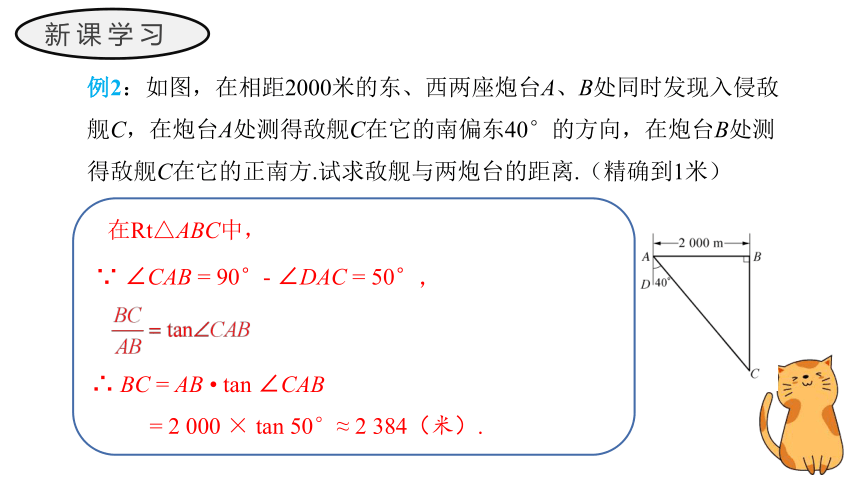
例2:如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
在Rt△ABC中,
∵ ∠CAB = 90°- ∠DAC = 50°,
∴ BC = AB tan ∠CAB
= 2 000 × tan 50°≈ 2 384(米).
新课学习
例2:如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
∵
∴
本题是已知两直角一边、一锐角,求其他两边.
答:敌舰与A、B两炮台的距离分别约为3111米和2384米
新课学习
解直角三角形的两种情况
(1)已知两条边;
(2)已知一条边和一个锐角.
注意:在解直角三角形的过程中,常会遇到近似计算,除了特别说明,这些角度都精确到1°
新课学习
拓展:解直角三角形的思想与方法
1.数形结合思想
2.方程思想
3.转化(化归)思想
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
新课学习
练一练:在 Rt△ABC 中,∠C=90°,a = 30,b = 20,求出c以及∠A和∠B.
A
B
C
b = 20
a = 30
c
根据勾股定理得
∴∠A≈56.3°
∴∠B=90° -∠A≈90° -56.3°≈33.7°
新课学习
拓展:解题方法
紧扣以下两种思路去求解:
(1)求边时,一般用未知边比已知边(或已知边比未知边),去找已知角的某一个锐角三角函数.
(2)求角时,一般用已知边比已知边,去找未知角的某一个锐角三角函数.
新课学习
练一练:在电线杆离地面8 米高处向地面拉一条缆绳,缆绳和地面成53°7′角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离.(精确到0.1米)
53°7′
A
B
C
在Rt△ABC中,AB = 8 米,∠C = 53°7′
答:缆绳的长约为10.0米,缆绳地面固定点到电线杆底部的距离约为6.0米.
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
5
课堂总结
1.解三角形的概念
2.解直角三角形的两种情况
THANK YOU
24.4 解直角三角形
(第一课时)
学习目标
1. 会运用直角三角形的两个锐角互余及锐角三角函数解直角三角形(重点)
2. 能够把实际问题转化成解直角三角形的问题(难点)
新课导入
我们前面学习了直角三角形的有关性质以及边角之间的各种关系,这些性质在我们生活中有什么作用吗?在我们生活中有什么应用吗?
这节课我们将学习直角三角形在生活中的应用.
新课学习
例1:如图,一棵大树在一次强烈的地震中于离地面5 米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少?
新课学习
利用勾股定理可以求出折断后倒下部分的长度为
13 + 5 =18 (米).
答:大树在折断之前高 18 米.
新课学习
解直角三角形的概念
在直角三角形中,由已知的元素求出未知元素的过程,叫做解直角三角形.
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
新课学习
例2:如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
在Rt△ABC中,
∵ ∠CAB = 90°- ∠DAC = 50°,
∴ BC = AB tan ∠CAB
= 2 000 × tan 50°≈ 2 384(米).
新课学习
例2:如图,在相距2000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
∵
∴
本题是已知两直角一边、一锐角,求其他两边.
答:敌舰与A、B两炮台的距离分别约为3111米和2384米
新课学习
解直角三角形的两种情况
(1)已知两条边;
(2)已知一条边和一个锐角.
注意:在解直角三角形的过程中,常会遇到近似计算,除了特别说明,这些角度都精确到1°
新课学习
拓展:解直角三角形的思想与方法
1.数形结合思想
2.方程思想
3.转化(化归)思想
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
新课学习
练一练:在 Rt△ABC 中,∠C=90°,a = 30,b = 20,求出c以及∠A和∠B.
A
B
C
b = 20
a = 30
c
根据勾股定理得
∴∠A≈56.3°
∴∠B=90° -∠A≈90° -56.3°≈33.7°
新课学习
拓展:解题方法
紧扣以下两种思路去求解:
(1)求边时,一般用未知边比已知边(或已知边比未知边),去找已知角的某一个锐角三角函数.
(2)求角时,一般用已知边比已知边,去找未知角的某一个锐角三角函数.
新课学习
练一练:在电线杆离地面8 米高处向地面拉一条缆绳,缆绳和地面成53°7′角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离.(精确到0.1米)
53°7′
A
B
C
在Rt△ABC中,AB = 8 米,∠C = 53°7′
答:缆绳的长约为10.0米,缆绳地面固定点到电线杆底部的距离约为6.0米.
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
5
课堂总结
1.解三角形的概念
2.解直角三角形的两种情况
THANK YOU
