24.3 锐角三角函数(第一课时) 课件(共28张PPT) 华东师大(2012)九年级上册
文档属性
| 名称 | 24.3 锐角三角函数(第一课时) 课件(共28张PPT) 华东师大(2012)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 07:56:27 | ||
图片预览






文档简介
(共28张PPT)
24.3 锐角三角函数
(第一课时)
学习目标
1. 掌握锐角三角函数(正弦、余弦、正切)的概念(重点)
2. 能利用三角函数的定义求三角函数值(难点)
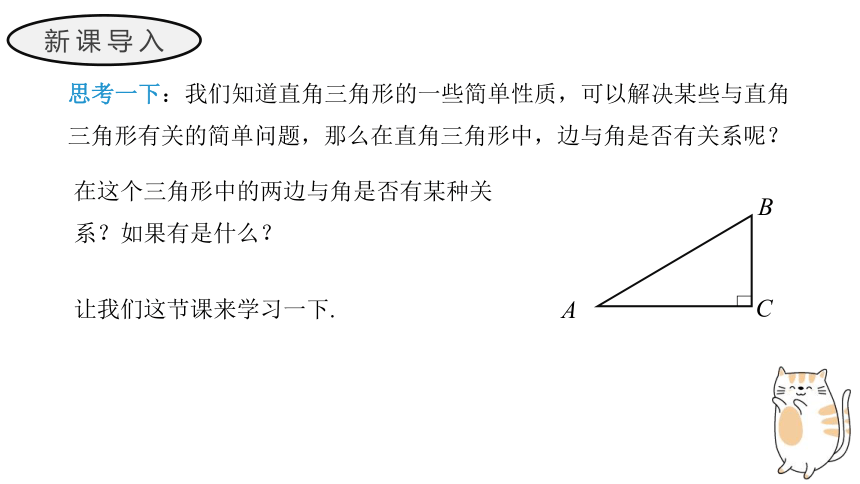
新课导入
思考一下:我们知道直角三角形的一些简单性质,可以解决某些与直角三角形有关的简单问题,那么在直角三角形中,边与角是否有关系呢?
A
B
C
在这个三角形中的两边与角是否有某种关系?如果有是什么?
让我们这节课来学习一下.
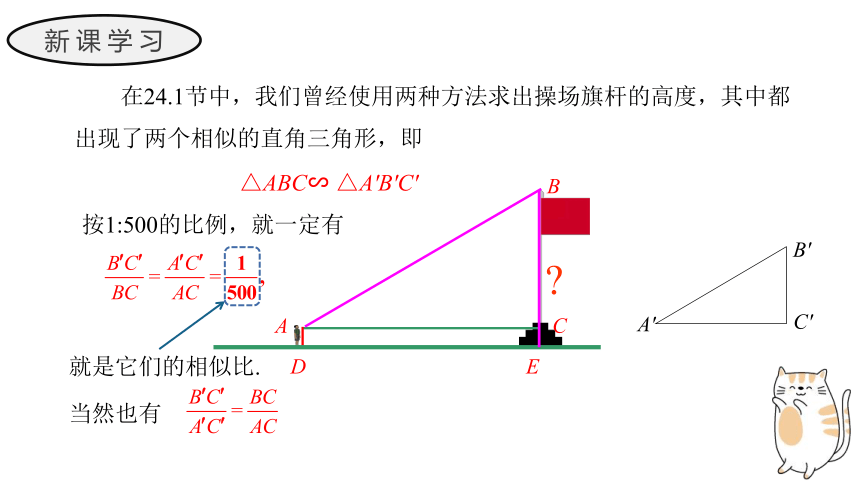
新课学习
在24.1节中,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的直角三角形,即
A
B
C
A′
B′
C′
D
E
△ABC∽ △A'B'C'
按1:500的比例,就一定有
就是它们的相似比.
当然也有
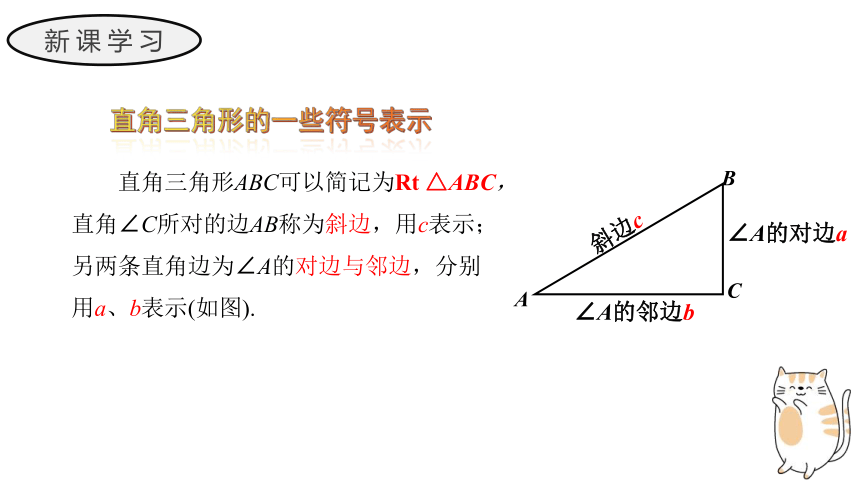
新课学习
直角三角形的一些符号表示
A
C
B
斜边c
∠A的对边a
∠A的邻边b
直角三角形ABC可以简记为Rt △ABC,直角∠C所对的边AB称为斜边,用c表示;另两条直角边为∠A的对边与邻边,分别用a、b表示(如图).
新课学习
思考一下:一般情况下,在 Rt△ABC 中,当锐角∠A取其他确定值时,∠A的对边与邻边的比值还会是一个固定值吗
前面结论的启示:在Rt △ABC中,只要一个锐角的大小不变(如∠A = 34°) ,那么不管这个直角三角形的大小如何,该锐角的对边与邻边的比值都是一个固定的值.
新课学习
探究一下:观察图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
A
C2
B2
C3
B3
有什么关系?
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
∴
结论:在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与斜边的比值都是唯一确定的.
新课学习
∠A 的正弦的概念
如图,在 Rt△ABC 中,∠C=90°,∠A 的对边与斜边的比叫做∠A 的正弦,记作 sin A , 即
A
B
C
c
a
b
对边
斜边
新课学习
探究一下:观察图中的Rt△AB1C1, Rt△AB2C2,Rt△AB3C3,则
有什么关系呢?
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
A
C2
B2
C3
B3
∴
结论:在Rt△ABC中,对于锐角∠A的每一个确定的值,其邻边与斜边的比值都是唯一确定的.
新课学习
∠A 的余弦的概念
如图,在 Rt△ABC 中,∠C = 90°,我们把锐角∠A 的邻边与斜边的比叫做∠A 的余弦 ,记作 cos A,即
A
B
C
c
a
b
对边
斜边
新课学习
探究一下:观察图中的Rt△AB1C1, Rt△AB2C2, Rt△AB3C3,则
有什么关系呢?
A
C2
B2
C3
B3
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
∴
结论:在Rt△ABC 中,对于锐角∠A的每一个确定的值,其对边与邻边的比值都是唯一确定的.
新课学习
A
B
C
c
a
b
对边
斜边
如图,在Rt△ABC 中,∠C = 90°,我们把锐角 A 的对边与邻边的比叫做∠A的正切,记作 tanA,即
∠A 的正切的概念
新课学习
三角函数的概念
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
三角函数的一些性质:
1.锐角三角函数值都是正实数,并且 0 < sin A < 1,0 < cos A < 1.
2.根据三角函数的定义,我们还可以得出 sin2A + cos2A = 1 .
新课学习
思考一下:为什么0 < sin A < 1,0 < cos A < 1成立?
在三角形中,正弦是对边比斜边,余弦是邻边比斜边.因为锐角三角形的边长都是正数,所以比值肯定是正的,所以sinA与cosA都大于0.
斜边是直角三角形中最长的边,所以对边或邻边都会比斜边短,所以它们的比值肯定小于1.这样就能得出0 < sinA < 1和0 < cosA < 1了.
新课学习
例1:如图,在 Rt△ABC 中,∠C = 90°,AC=15,BC=8,试求出∠A的三个三角函数值.
A
B
C
8
15
AB = = = 17
sinA = =
cosA = =
tanA = =
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
课堂总结
1.∠A的正弦
2.∠A的余弦
3.∠A的正切
THANK YOU
24.3 锐角三角函数
(第一课时)
学习目标
1. 掌握锐角三角函数(正弦、余弦、正切)的概念(重点)
2. 能利用三角函数的定义求三角函数值(难点)
新课导入
思考一下:我们知道直角三角形的一些简单性质,可以解决某些与直角三角形有关的简单问题,那么在直角三角形中,边与角是否有关系呢?
A
B
C
在这个三角形中的两边与角是否有某种关系?如果有是什么?
让我们这节课来学习一下.
新课学习
在24.1节中,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的直角三角形,即
A
B
C
A′
B′
C′
D
E
△ABC∽ △A'B'C'
按1:500的比例,就一定有
就是它们的相似比.
当然也有
新课学习
直角三角形的一些符号表示
A
C
B
斜边c
∠A的对边a
∠A的邻边b
直角三角形ABC可以简记为Rt △ABC,直角∠C所对的边AB称为斜边,用c表示;另两条直角边为∠A的对边与邻边,分别用a、b表示(如图).
新课学习
思考一下:一般情况下,在 Rt△ABC 中,当锐角∠A取其他确定值时,∠A的对边与邻边的比值还会是一个固定值吗
前面结论的启示:在Rt △ABC中,只要一个锐角的大小不变(如∠A = 34°) ,那么不管这个直角三角形的大小如何,该锐角的对边与邻边的比值都是一个固定的值.
新课学习
探究一下:观察图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
A
C2
B2
C3
B3
有什么关系?
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
∴
结论:在Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与斜边的比值都是唯一确定的.
新课学习
∠A 的正弦的概念
如图,在 Rt△ABC 中,∠C=90°,∠A 的对边与斜边的比叫做∠A 的正弦,记作 sin A , 即
A
B
C
c
a
b
对边
斜边
新课学习
探究一下:观察图中的Rt△AB1C1, Rt△AB2C2,Rt△AB3C3,则
有什么关系呢?
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
A
C2
B2
C3
B3
∴
结论:在Rt△ABC中,对于锐角∠A的每一个确定的值,其邻边与斜边的比值都是唯一确定的.
新课学习
∠A 的余弦的概念
如图,在 Rt△ABC 中,∠C = 90°,我们把锐角∠A 的邻边与斜边的比叫做∠A 的余弦 ,记作 cos A,即
A
B
C
c
a
b
对边
斜边
新课学习
探究一下:观察图中的Rt△AB1C1, Rt△AB2C2, Rt△AB3C3,则
有什么关系呢?
A
C2
B2
C3
B3
易知:Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
∴
结论:在Rt△ABC 中,对于锐角∠A的每一个确定的值,其对边与邻边的比值都是唯一确定的.
新课学习
A
B
C
c
a
b
对边
斜边
如图,在Rt△ABC 中,∠C = 90°,我们把锐角 A 的对边与邻边的比叫做∠A的正切,记作 tanA,即
∠A 的正切的概念
新课学习
三角函数的概念
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
三角函数的一些性质:
1.锐角三角函数值都是正实数,并且 0 < sin A < 1,0 < cos A < 1.
2.根据三角函数的定义,我们还可以得出 sin2A + cos2A = 1 .
新课学习
思考一下:为什么0 < sin A < 1,0 < cos A < 1成立?
在三角形中,正弦是对边比斜边,余弦是邻边比斜边.因为锐角三角形的边长都是正数,所以比值肯定是正的,所以sinA与cosA都大于0.
斜边是直角三角形中最长的边,所以对边或邻边都会比斜边短,所以它们的比值肯定小于1.这样就能得出0 < sinA < 1和0 < cosA < 1了.
新课学习
例1:如图,在 Rt△ABC 中,∠C = 90°,AC=15,BC=8,试求出∠A的三个三角函数值.
A
B
C
8
15
AB = = = 17
sinA = =
cosA = =
tanA = =
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
课堂总结
1.∠A的正弦
2.∠A的余弦
3.∠A的正切
THANK YOU
