24.2 直角三角形的性质 课件(共26张PPT) 华东师大(2012)九年级上册
文档属性
| 名称 | 24.2 直角三角形的性质 课件(共26张PPT) 华东师大(2012)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 07:59:46 | ||
图片预览


文档简介
(共26张PPT)
24.2 直角三角形的性质
学习目标
1.探索并掌握直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半(重点)
2.能够应用直角三角形的性质定理解决几何问题(难点)
新课导入
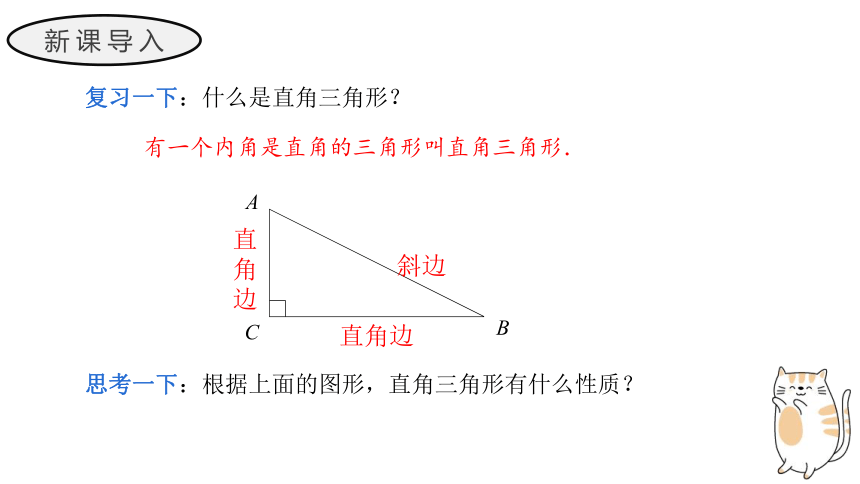
复习一下:什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
A
C
B
斜边
直角边
直角边
思考一下:根据上面的图形,直角三角形有什么性质?
新课学习
C
A
B
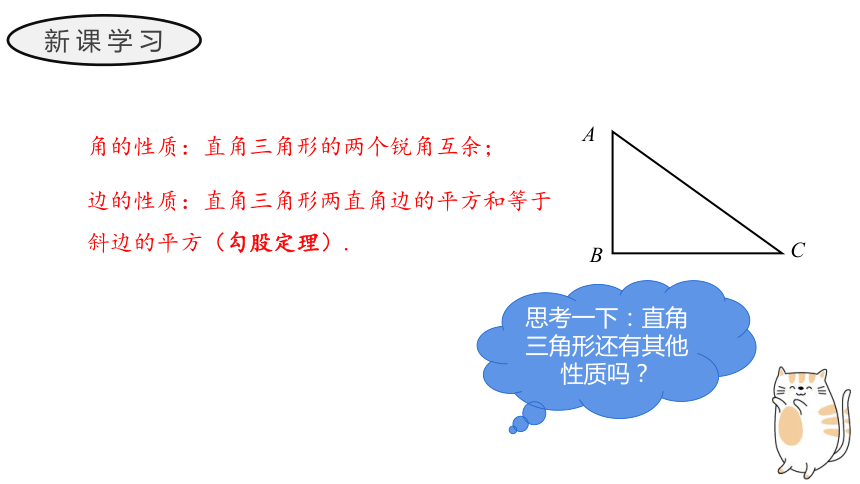
角的性质:直角三角形的两个锐角互余;
边的性质:直角三角形两直角边的平方和等于斜边的平方(勾股定理).
思考一下:直角三角形还有其他性质吗?
新课学习
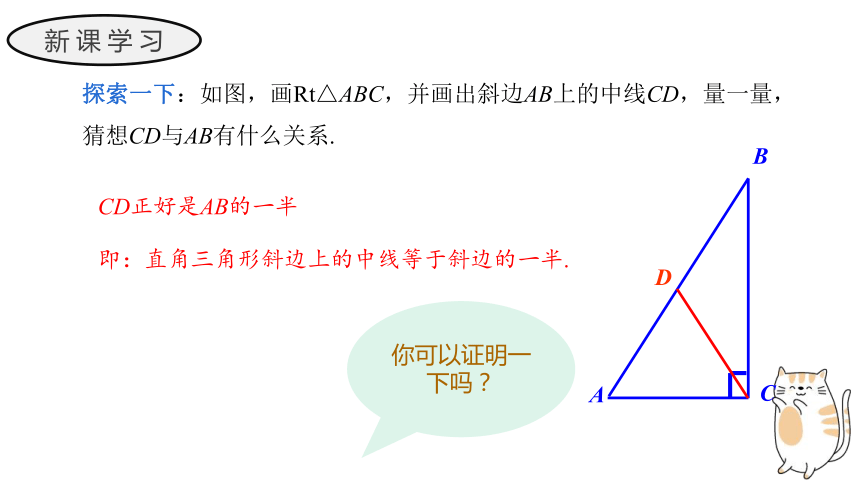
探索一下:如图,画Rt△ABC,并画出斜边AB上的中线CD,量一量,猜想CD与AB有什么关系.
A
B
C
D
CD正好是AB的一半
即:直角三角形斜边上的中线等于斜边的一半.
你可以证明一下吗?
新课学习
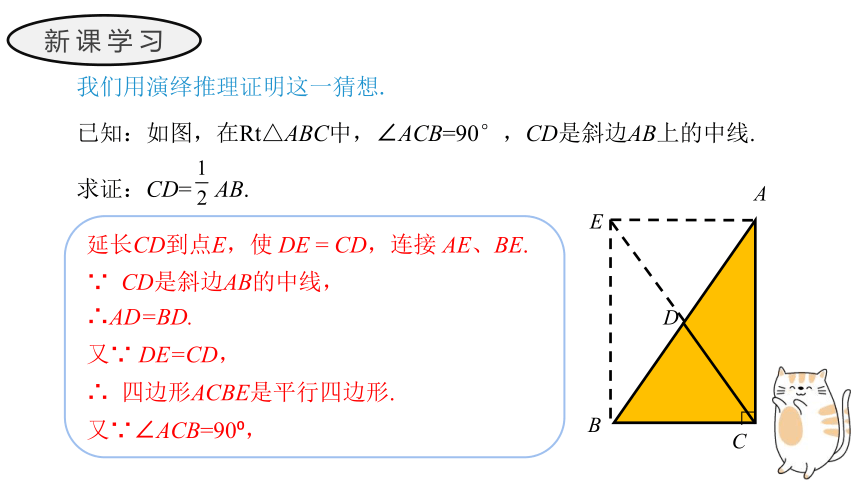
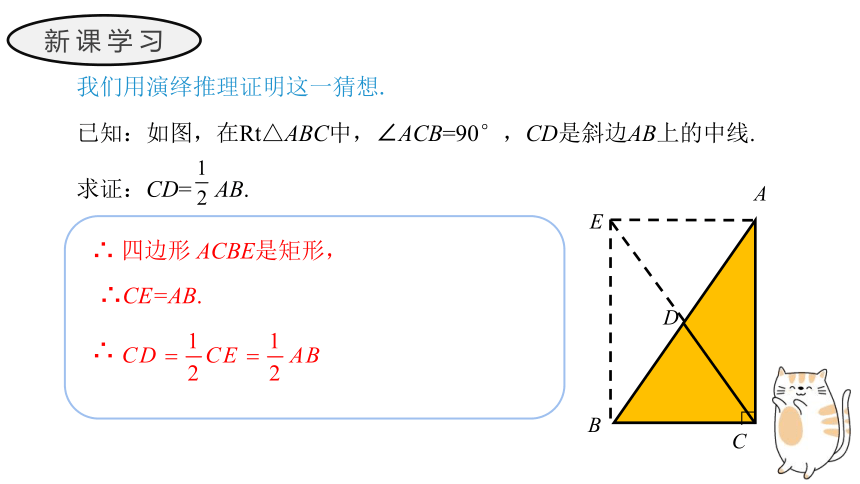
我们用演绎推理证明这一猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
A
B
C
∟
D
E
延长CD到点E,使 DE = CD,连接 AE、BE.
∵ CD是斜边AB的中线,
∴AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
新课学习
我们用演绎推理证明这一猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
A
B
C
∟
D
E
∴ 四边形 ACBE是矩形,
∴
∴CE=AB.
新课学习
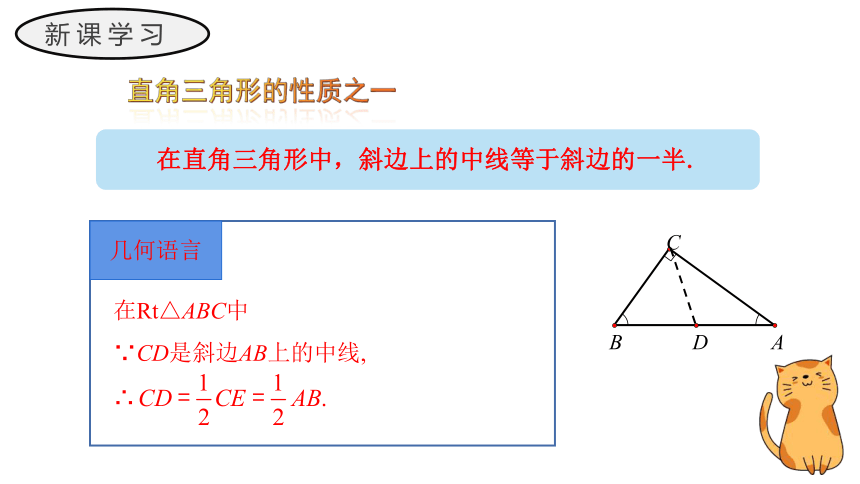
直角三角形的性质之一
在直角三角形中,斜边上的中线等于斜边的一半.
几何语言
C
B
A
D
在Rt△ABC中
∵CD是斜边AB上的中线,
新课学习
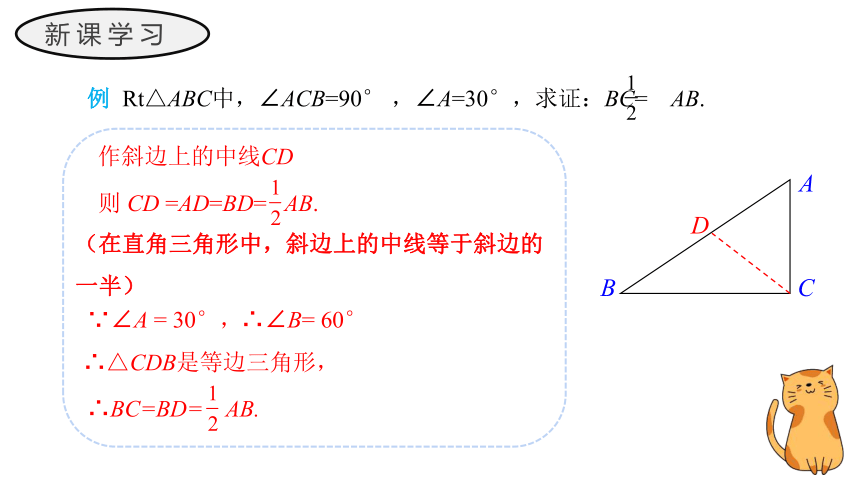
例 Rt△ABC中,∠ACB=90° ,∠A=30°,求证:BC= AB.
C
B
A
D
作斜边上的中线CD
则 CD =AD=BD= AB.
(在直角三角形中,斜边上的中线等于斜边的一半)
∵∠A = 30°,
∴∠B= 60°
∴△CDB是等边三角形,
∴BC=BD= AB.
新课学习
直角三角形的性质之一
根据上面的例题,我们可以得到
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言
C
B
A
D
∵ ∠ACB=90 °,∠A=30°
∴ BC= AB
新课学习
练一练:如图,在A岛周围20海里水域有暗礁,一艘轮船由西向东航行到点О处时,发现A岛在北偏东60°的方向,且与轮船相距30 海里.该船如果不改变航向,有触暗礁的危险吗
O
A
B
D
60°
东
30 海里
新课学习
O
A
B
D
60°
东
30 海里
在Rt△AOD中,
∠AOD=30°, AO=30 海里,
∴AD= AO= ×30 ≈ 25.98(海里) > 20海里,
∴该船如果不改变航向,没有触暗礁的危险.
新课学习
练一练:小明沿倾斜角为30°的山坡,从山脚步行到山顶的革命烈士纪念碑,共走了120m.求山顶的高度.
A
B
C
由题意可画出如图的直角三角形.
其中AB=120m,∠B=30°.
由30°角所对直角边等于斜边的一半可知AC=60m.
即山顶的高度为60m.
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
课堂总结
1.在直角三角形中,斜边上的中线等于斜边的一半.
2. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
THANK YOU
24.2 直角三角形的性质
学习目标
1.探索并掌握直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半(重点)
2.能够应用直角三角形的性质定理解决几何问题(难点)
新课导入
复习一下:什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
A
C
B
斜边
直角边
直角边
思考一下:根据上面的图形,直角三角形有什么性质?
新课学习
C
A
B
角的性质:直角三角形的两个锐角互余;
边的性质:直角三角形两直角边的平方和等于斜边的平方(勾股定理).
思考一下:直角三角形还有其他性质吗?
新课学习
探索一下:如图,画Rt△ABC,并画出斜边AB上的中线CD,量一量,猜想CD与AB有什么关系.
A
B
C
D
CD正好是AB的一半
即:直角三角形斜边上的中线等于斜边的一半.
你可以证明一下吗?
新课学习
我们用演绎推理证明这一猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
A
B
C
∟
D
E
延长CD到点E,使 DE = CD,连接 AE、BE.
∵ CD是斜边AB的中线,
∴AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
新课学习
我们用演绎推理证明这一猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
A
B
C
∟
D
E
∴ 四边形 ACBE是矩形,
∴
∴CE=AB.
新课学习
直角三角形的性质之一
在直角三角形中,斜边上的中线等于斜边的一半.
几何语言
C
B
A
D
在Rt△ABC中
∵CD是斜边AB上的中线,
新课学习
例 Rt△ABC中,∠ACB=90° ,∠A=30°,求证:BC= AB.
C
B
A
D
作斜边上的中线CD
则 CD =AD=BD= AB.
(在直角三角形中,斜边上的中线等于斜边的一半)
∵∠A = 30°,
∴∠B= 60°
∴△CDB是等边三角形,
∴BC=BD= AB.
新课学习
直角三角形的性质之一
根据上面的例题,我们可以得到
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言
C
B
A
D
∵ ∠ACB=90 °,∠A=30°
∴ BC= AB
新课学习
练一练:如图,在A岛周围20海里水域有暗礁,一艘轮船由西向东航行到点О处时,发现A岛在北偏东60°的方向,且与轮船相距30 海里.该船如果不改变航向,有触暗礁的危险吗
O
A
B
D
60°
东
30 海里
新课学习
O
A
B
D
60°
东
30 海里
在Rt△AOD中,
∠AOD=30°, AO=30 海里,
∴AD= AO= ×30 ≈ 25.98(海里) > 20海里,
∴该船如果不改变航向,没有触暗礁的危险.
新课学习
练一练:小明沿倾斜角为30°的山坡,从山脚步行到山顶的革命烈士纪念碑,共走了120m.求山顶的高度.
A
B
C
由题意可画出如图的直角三角形.
其中AB=120m,∠B=30°.
由30°角所对直角边等于斜边的一半可知AC=60m.
即山顶的高度为60m.
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
课堂总结
1.在直角三角形中,斜边上的中线等于斜边的一半.
2. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
THANK YOU
