25.2.3 列举所有机会均等的结果 课件(共30张PPT) 华东师大(2012)九年级上册
文档属性
| 名称 | 25.2.3 列举所有机会均等的结果 课件(共30张PPT) 华东师大(2012)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 08:00:28 | ||
图片预览









文档简介
(共30张PPT)
25.2.3 列举所有机会均等的结果
学习目标
1. 会用列表法、画树状图法计算概率(重点)
2. 区分什么时候用列表法,什么时候用树状图(重点)
3. 通过比较概率大小做出合理决策(难点)
新课导入
例4:抛掷一枚普通硬币3次. 有人说“连续掷出三个正面”和“先掷出两个正面,再掷出一个反面”的概率是一样的. 你同意吗?
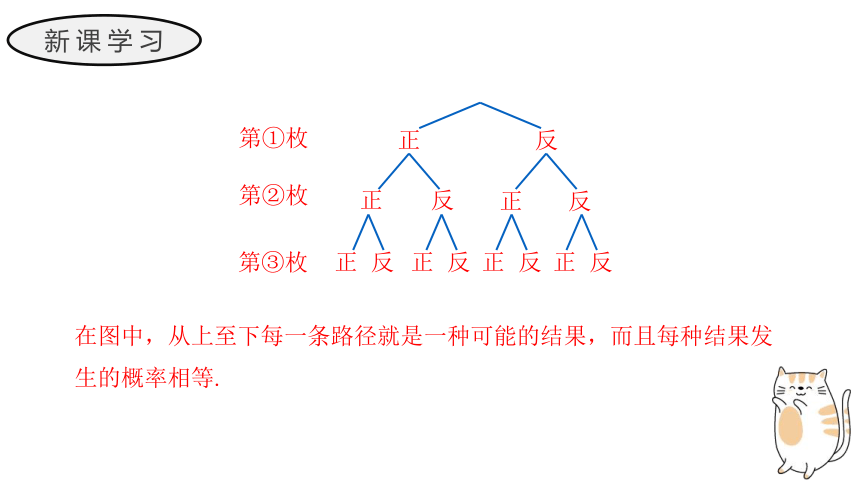
分析:对于第1次抛掷,可能出现的结果是正面或反面,对于第2、3次抛掷来说也是这样. 而且每次硬币出现正面或反面的概率都相等. 由此,我们可以画出树状图,如图所示. 在图中,从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
新课学习
正
反
正
反
正
反
正
反
正
反
正
反
正
反
第①枚
第②枚
第③枚
在图中,从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
新课学习
抛掷一枚普通硬币 3 次,共有以下 8 种机会均等的结果:
正正正,正正反,正反正,正反反,反正正,反正反,反反正,反反反.
P( 正正正 ) = P( 正正反 ) = .
所以,例题中的说法正确.
新课学习
思考一下:根据上面的例题,你可以总结一下树状图的优点吗?
该树状图从上到下,列举了所有机会均等的结果,可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明.
新课学习
思考一下:有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现 4 种结果:
(1) 全是正面; (2) 两正一反;
(3) 两反一正; (4) 全是反面.
因此这四个事件出现的概率相等. 你同意这种说法吗?为什么?
不同意,由树状图可以看出,共有8种等可能的结果. 其中,“全是正面”出现了1次,“两正一反”出现了3次,“全是反面”出现了1次. 因此,(1)和(4)出现的频率相等,但(1)、(4)出现的概率比(2)、(3)出现的概率小.
新课学习
问题5:口袋中装有 1 个红球和 2 个白球,搅匀后从中摸出 1 个球,放回搅匀,再摸出第 2 个球,两次摸球就可能出现 3 种结果:
(1) 都是红球;(2) 都是白球;(3) 一红一白.
这三个事件发生的概率相等吗?
新课学习
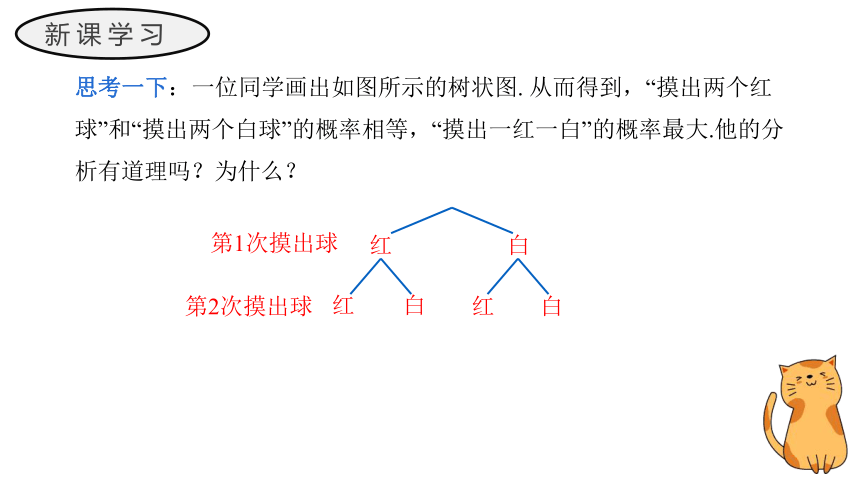
思考一下:一位同学画出如图所示的树状图. 从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.他的分析有道理吗?为什么?
红
白
红
白
红
白
第1次摸出球
第2次摸出球
新课学习
分析:把两个白球分别记作白1和白2. 如图,用画树状图的方法看看有哪些等可能的结果:
红
白1
红
白1
白2
红
白1
白2
白2
白1
红
白2
第1次摸出球
第2次摸出球
从中可以看出,一共有 9 种等可能的结果.
在“摸出两红”、“摸出两白”、“摸出一红一白”这三个事件中,“摸出两红”的概率最小,等于
“摸出两白”和“摸出一白一红”的概率相等,都是 .
新课学习
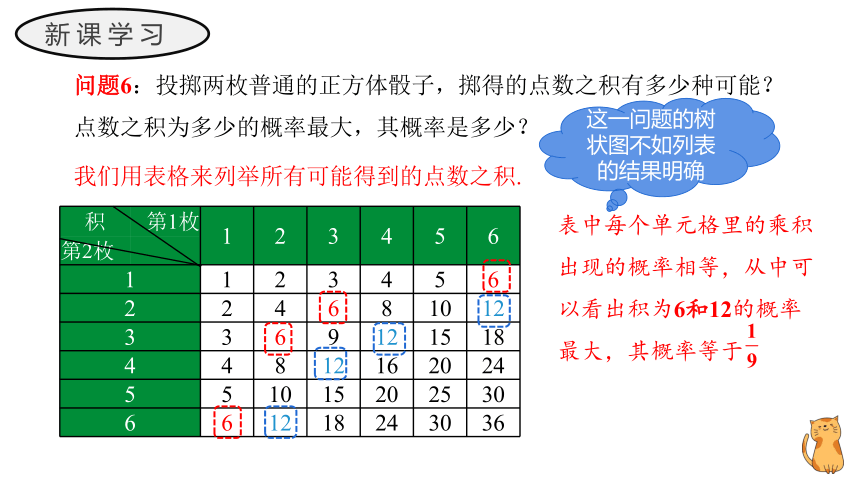
问题6:投掷两枚普通的正方体骰子,掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
我们用表格来列举所有可能得到的点数之积.
积 第1枚 1 2 3 4 5 6
第2枚 1 1 2 3 4 5 6
2 2 4 6 8 10 12
3 3 6 9 12 15 18
4 4 8 12 16 20 24
5 5 10 15 20 25 30
6 6 12 18 24 30 36
表中每个单元格里的乘积出现的概率相等,从中可以看出积为6和12的概率最大,其概率等于
这一问题的树状图不如列表的结果明确
新课学习
问题7:“石头、剪刀、布”是一个广为流传的游戏,游戏时,甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负.
假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势 ( 即不分胜负 ) 的概率是多少?
分析:如图,画出树状图:
新课学习
甲
乙
结果
石头
石头
剪刀
布
(石头,石头)
(石头,剪刀)
(石头,布)
剪刀
石头
剪刀
布
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
布
石头
剪刀
布
(布,石头)
(布,剪刀)
(布,布)
新课学习
所有机会均等的结果有 9 种,其中的 3种 —— ( 石头 , 石头 )、( 剪刀 , 剪刀 )、( 布 , 布 )是我们关注的结果,
所以 P(同种手势) =
=
新课学习
画树状图求概率的基本步骤:
1.弄清楚一次试验的几个步骤及顺序;
2.列举一次试验的所有可能结果;
3.数出随机事件A包含的结果数m,试验的所有可能结果数n;
4.用概率公式进行计算.
新课学习
思考一下:什么时候用树状图,什么时候用列表法?
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
当一次试验要涉及两个以上因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用画树状图的办法.
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
课堂巩固
课堂总结
1.画树状图的基本步骤
2.树状图与列表法的使用
THANK YOU
25.2.3 列举所有机会均等的结果
学习目标
1. 会用列表法、画树状图法计算概率(重点)
2. 区分什么时候用列表法,什么时候用树状图(重点)
3. 通过比较概率大小做出合理决策(难点)
新课导入
例4:抛掷一枚普通硬币3次. 有人说“连续掷出三个正面”和“先掷出两个正面,再掷出一个反面”的概率是一样的. 你同意吗?
分析:对于第1次抛掷,可能出现的结果是正面或反面,对于第2、3次抛掷来说也是这样. 而且每次硬币出现正面或反面的概率都相等. 由此,我们可以画出树状图,如图所示. 在图中,从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
新课学习
正
反
正
反
正
反
正
反
正
反
正
反
正
反
第①枚
第②枚
第③枚
在图中,从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
新课学习
抛掷一枚普通硬币 3 次,共有以下 8 种机会均等的结果:
正正正,正正反,正反正,正反反,反正正,反正反,反反正,反反反.
P( 正正正 ) = P( 正正反 ) = .
所以,例题中的说法正确.
新课学习
思考一下:根据上面的例题,你可以总结一下树状图的优点吗?
该树状图从上到下,列举了所有机会均等的结果,可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明.
新课学习
思考一下:有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现 4 种结果:
(1) 全是正面; (2) 两正一反;
(3) 两反一正; (4) 全是反面.
因此这四个事件出现的概率相等. 你同意这种说法吗?为什么?
不同意,由树状图可以看出,共有8种等可能的结果. 其中,“全是正面”出现了1次,“两正一反”出现了3次,“全是反面”出现了1次. 因此,(1)和(4)出现的频率相等,但(1)、(4)出现的概率比(2)、(3)出现的概率小.
新课学习
问题5:口袋中装有 1 个红球和 2 个白球,搅匀后从中摸出 1 个球,放回搅匀,再摸出第 2 个球,两次摸球就可能出现 3 种结果:
(1) 都是红球;(2) 都是白球;(3) 一红一白.
这三个事件发生的概率相等吗?
新课学习
思考一下:一位同学画出如图所示的树状图. 从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.他的分析有道理吗?为什么?
红
白
红
白
红
白
第1次摸出球
第2次摸出球
新课学习
分析:把两个白球分别记作白1和白2. 如图,用画树状图的方法看看有哪些等可能的结果:
红
白1
红
白1
白2
红
白1
白2
白2
白1
红
白2
第1次摸出球
第2次摸出球
从中可以看出,一共有 9 种等可能的结果.
在“摸出两红”、“摸出两白”、“摸出一红一白”这三个事件中,“摸出两红”的概率最小,等于
“摸出两白”和“摸出一白一红”的概率相等,都是 .
新课学习
问题6:投掷两枚普通的正方体骰子,掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
我们用表格来列举所有可能得到的点数之积.
积 第1枚 1 2 3 4 5 6
第2枚 1 1 2 3 4 5 6
2 2 4 6 8 10 12
3 3 6 9 12 15 18
4 4 8 12 16 20 24
5 5 10 15 20 25 30
6 6 12 18 24 30 36
表中每个单元格里的乘积出现的概率相等,从中可以看出积为6和12的概率最大,其概率等于
这一问题的树状图不如列表的结果明确
新课学习
问题7:“石头、剪刀、布”是一个广为流传的游戏,游戏时,甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负.
假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势 ( 即不分胜负 ) 的概率是多少?
分析:如图,画出树状图:
新课学习
甲
乙
结果
石头
石头
剪刀
布
(石头,石头)
(石头,剪刀)
(石头,布)
剪刀
石头
剪刀
布
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
布
石头
剪刀
布
(布,石头)
(布,剪刀)
(布,布)
新课学习
所有机会均等的结果有 9 种,其中的 3种 —— ( 石头 , 石头 )、( 剪刀 , 剪刀 )、( 布 , 布 )是我们关注的结果,
所以 P(同种手势) =
=
新课学习
画树状图求概率的基本步骤:
1.弄清楚一次试验的几个步骤及顺序;
2.列举一次试验的所有可能结果;
3.数出随机事件A包含的结果数m,试验的所有可能结果数n;
4.用概率公式进行计算.
新课学习
思考一下:什么时候用树状图,什么时候用列表法?
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
当一次试验要涉及两个以上因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用画树状图的办法.
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
课堂巩固
课堂总结
1.画树状图的基本步骤
2.树状图与列表法的使用
THANK YOU
