25.1 在重复试验中观察不确定现象 课件(共28张PPT) 华东师大(2012)九年级上册
文档属性
| 名称 | 25.1 在重复试验中观察不确定现象 课件(共28张PPT) 华东师大(2012)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 08:03:02 | ||
图片预览








文档简介
(共28张PPT)
25.1 在重复试验中观察不确定现象
学习目标
1.理解并掌握确定事件与随机事件的含义与区别(重点)
2.能够对于事件发生的情况进行判断 (重点)
3.运用事件的频率的稳定性估计事件发生的机会大小(难点)
新课导入
思考一下:掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有 1 到 6 个的点数,请考虑以下的问题:掷一次骰子,在骰子向上的一面上,
1.出现的点数会是 7 吗?
是不可能的,出现的点数绝对不会大于 6.
2.出现的点数会小于7 吗?
是必然的.
新课学习
必然事件的概念
我们称无需通过试验就能预先确定它们在每次试验中都一定会发生的事件为必然事件.
不可能事件的概念
称在每次试验中都一定不会发生的事件为不可能事件.
必然事件和不可能事件在试验中是否发生都是我们能够预先确定的,所以统称为确定事件.
新课学习
思考一下:掷一个质地均匀的正方形骰子,思考一下出现的点数会是 2 吗?出现的点数是奇数呢?
这两件事是可能发生的,因为掷一个骰子从 1 至 6 都有可能出现,当出现1,3,5时,这是掷出的就是奇数了.
这就是随机事件
无法预先确定在一次试验中会不会发生的事件,我们称这样的事件为随机事件.
新课学习
做一做:准备三张大小一样的纸片,上面印有不同的图案(如照片、明信片、自己画的图片等),把每张纸片都对折,剪成大小一样的两张(如图所示).将这六张小纸片有图案的一面朝下,然后混合,让你的同伴随机抽出两张小纸片. 你认为抽出的那两张小纸片正好能成功拼成原图的机会大吗?猜一猜,大概平均几次里会有一次成功呢?
新课学习
思考一下:在这个游戏中,你关注的是哪一个随机事件? 在总的试验次数中,你观察到它成功的次数多还是失败的次数多?成功的机会是50%吗?你觉得这个观察结果合乎情理吗?
在一次试验中,虽然某个随机事件要么发生,要么不发生,但是它发生与不发生的机会并非“各占一半”.
随机事件发生机会的大小介于0与1之间,不能简单说成50%.
新课学习
思考一下:通过做一做,你能得到什么启示?
随机事件是否发生,没有人可以预测,这叫做“随机性”,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们就可以用频率估计随机事件在每次试验时发生的机会的大小.
新课学习
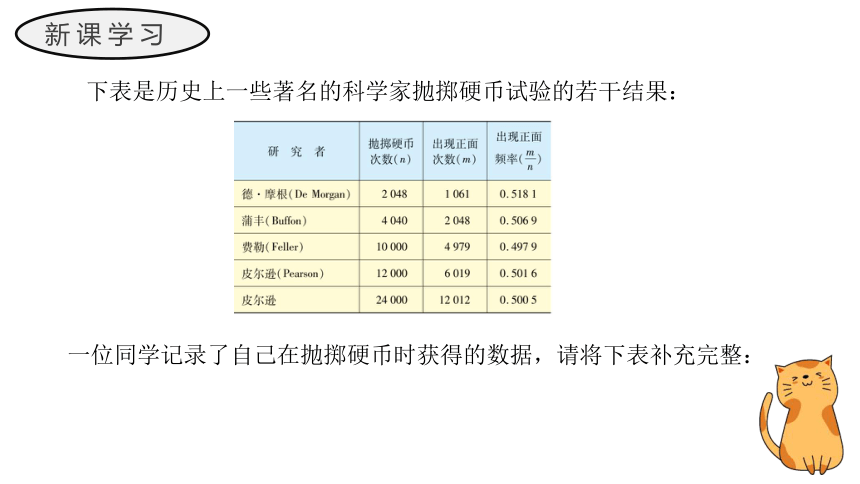
下表是历史上一些著名的科学家抛掷硬币试验的若干结果:
一位同学记录了自己在抛掷硬币时获得的数据,请将下表补充完整:
新课学习
抛掷次数 50 100 150 200 250 300 350 400
出现正面的频数 26 53 72 94 116 142 169 193
出现正面的频率 52.0% 53.0% 48.0% 47.0% 46.4% 47.3% 48.3% 48.3%
抛掷次数 450 500 550 600 650 700 750 800
出现正面的频数 218 242 269 294 321 343 369 395
出现正面的频率
48.4%
48.4%
48.9%
49.0%
49.4%
49.0%
49.2%
49.4%
新课学习
思考一下:折线图显示,当试验次数比较多的时候,“出现正面”的频率波动明显减小,表现为“风平浪静”,且“出现正面”的频率在0.5附近波动.如果换成其他试验,是否也能发现类似的规律呢?
也会发现的
思考一下:在试验中,“出现两个正面”的频率稳定在多少附近,“出现一正一反”的频率稳定在多少附近?
25%
25%
新课学习
用频率估计事件发生的机会
随着试验次数的增加,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们可以用频率估计随机事件在每次试验时发生的机会的大小.
新课学习
练一练:下面是两位同学对抛掷硬币问题的不同说法,你认为有道理吗?为什么?
(1)抛掷一枚质量分布均匀的硬币,是“正”是“反”无法预测,全凭运气. 因此,抛掷1 000次的话也许只有200次“正”,也许会有700次“正”,没有什么规律;
没有道理. 因为虽然在每次抛掷中是“正”还是“反”无法预测,但随着抛掷次数的增加,“出现正面”和“出现反面”的频率均逐渐稳定在0.5附近,是有规律可循的.
新课学习
(2)抛掷一枚质量分布均匀的硬币,“出现正面”和“出现反面”的机会均等. 因此,抛掷1 000次的话,一定会有500次“正”,500次“反”.
没有道理. 因为虽然在抛掷一枚质量分布均匀的硬币时“出现正面”和“出现反面”的机会均0.5,但成功率(频率)并不等同于机会(概率),即使是多次抛掷以后,成功率(频率)也可能只是与机会(概率)接近,但不一定相等.
课堂巩固
A
课堂巩固
D
课堂巩固
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
1
2或者3
课堂巩固
课堂总结
1.必然事件的概念
2.不可能事件的概念
3.随机事件的概念
4.用频率估计随机事件发生的大小
THANK YOU
25.1 在重复试验中观察不确定现象
学习目标
1.理解并掌握确定事件与随机事件的含义与区别(重点)
2.能够对于事件发生的情况进行判断 (重点)
3.运用事件的频率的稳定性估计事件发生的机会大小(难点)
新课导入
思考一下:掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有 1 到 6 个的点数,请考虑以下的问题:掷一次骰子,在骰子向上的一面上,
1.出现的点数会是 7 吗?
是不可能的,出现的点数绝对不会大于 6.
2.出现的点数会小于7 吗?
是必然的.
新课学习
必然事件的概念
我们称无需通过试验就能预先确定它们在每次试验中都一定会发生的事件为必然事件.
不可能事件的概念
称在每次试验中都一定不会发生的事件为不可能事件.
必然事件和不可能事件在试验中是否发生都是我们能够预先确定的,所以统称为确定事件.
新课学习
思考一下:掷一个质地均匀的正方形骰子,思考一下出现的点数会是 2 吗?出现的点数是奇数呢?
这两件事是可能发生的,因为掷一个骰子从 1 至 6 都有可能出现,当出现1,3,5时,这是掷出的就是奇数了.
这就是随机事件
无法预先确定在一次试验中会不会发生的事件,我们称这样的事件为随机事件.
新课学习
做一做:准备三张大小一样的纸片,上面印有不同的图案(如照片、明信片、自己画的图片等),把每张纸片都对折,剪成大小一样的两张(如图所示).将这六张小纸片有图案的一面朝下,然后混合,让你的同伴随机抽出两张小纸片. 你认为抽出的那两张小纸片正好能成功拼成原图的机会大吗?猜一猜,大概平均几次里会有一次成功呢?
新课学习
思考一下:在这个游戏中,你关注的是哪一个随机事件? 在总的试验次数中,你观察到它成功的次数多还是失败的次数多?成功的机会是50%吗?你觉得这个观察结果合乎情理吗?
在一次试验中,虽然某个随机事件要么发生,要么不发生,但是它发生与不发生的机会并非“各占一半”.
随机事件发生机会的大小介于0与1之间,不能简单说成50%.
新课学习
思考一下:通过做一做,你能得到什么启示?
随机事件是否发生,没有人可以预测,这叫做“随机性”,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们就可以用频率估计随机事件在每次试验时发生的机会的大小.
新课学习
下表是历史上一些著名的科学家抛掷硬币试验的若干结果:
一位同学记录了自己在抛掷硬币时获得的数据,请将下表补充完整:
新课学习
抛掷次数 50 100 150 200 250 300 350 400
出现正面的频数 26 53 72 94 116 142 169 193
出现正面的频率 52.0% 53.0% 48.0% 47.0% 46.4% 47.3% 48.3% 48.3%
抛掷次数 450 500 550 600 650 700 750 800
出现正面的频数 218 242 269 294 321 343 369 395
出现正面的频率
48.4%
48.4%
48.9%
49.0%
49.4%
49.0%
49.2%
49.4%
新课学习
思考一下:折线图显示,当试验次数比较多的时候,“出现正面”的频率波动明显减小,表现为“风平浪静”,且“出现正面”的频率在0.5附近波动.如果换成其他试验,是否也能发现类似的规律呢?
也会发现的
思考一下:在试验中,“出现两个正面”的频率稳定在多少附近,“出现一正一反”的频率稳定在多少附近?
25%
25%
新课学习
用频率估计事件发生的机会
随着试验次数的增加,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们可以用频率估计随机事件在每次试验时发生的机会的大小.
新课学习
练一练:下面是两位同学对抛掷硬币问题的不同说法,你认为有道理吗?为什么?
(1)抛掷一枚质量分布均匀的硬币,是“正”是“反”无法预测,全凭运气. 因此,抛掷1 000次的话也许只有200次“正”,也许会有700次“正”,没有什么规律;
没有道理. 因为虽然在每次抛掷中是“正”还是“反”无法预测,但随着抛掷次数的增加,“出现正面”和“出现反面”的频率均逐渐稳定在0.5附近,是有规律可循的.
新课学习
(2)抛掷一枚质量分布均匀的硬币,“出现正面”和“出现反面”的机会均等. 因此,抛掷1 000次的话,一定会有500次“正”,500次“反”.
没有道理. 因为虽然在抛掷一枚质量分布均匀的硬币时“出现正面”和“出现反面”的机会均0.5,但成功率(频率)并不等同于机会(概率),即使是多次抛掷以后,成功率(频率)也可能只是与机会(概率)接近,但不一定相等.
课堂巩固
A
课堂巩固
D
课堂巩固
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
1
2或者3
课堂巩固
课堂总结
1.必然事件的概念
2.不可能事件的概念
3.随机事件的概念
4.用频率估计随机事件发生的大小
THANK YOU
