[专项培优]湘教版数学八年级下册第一章直角三角形(含答案)
文档属性
| 名称 | [专项培优]湘教版数学八年级下册第一章直角三角形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 415.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 16:42:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
[专项培优]湘教版数学八年级下册直角三角形
一、单选题
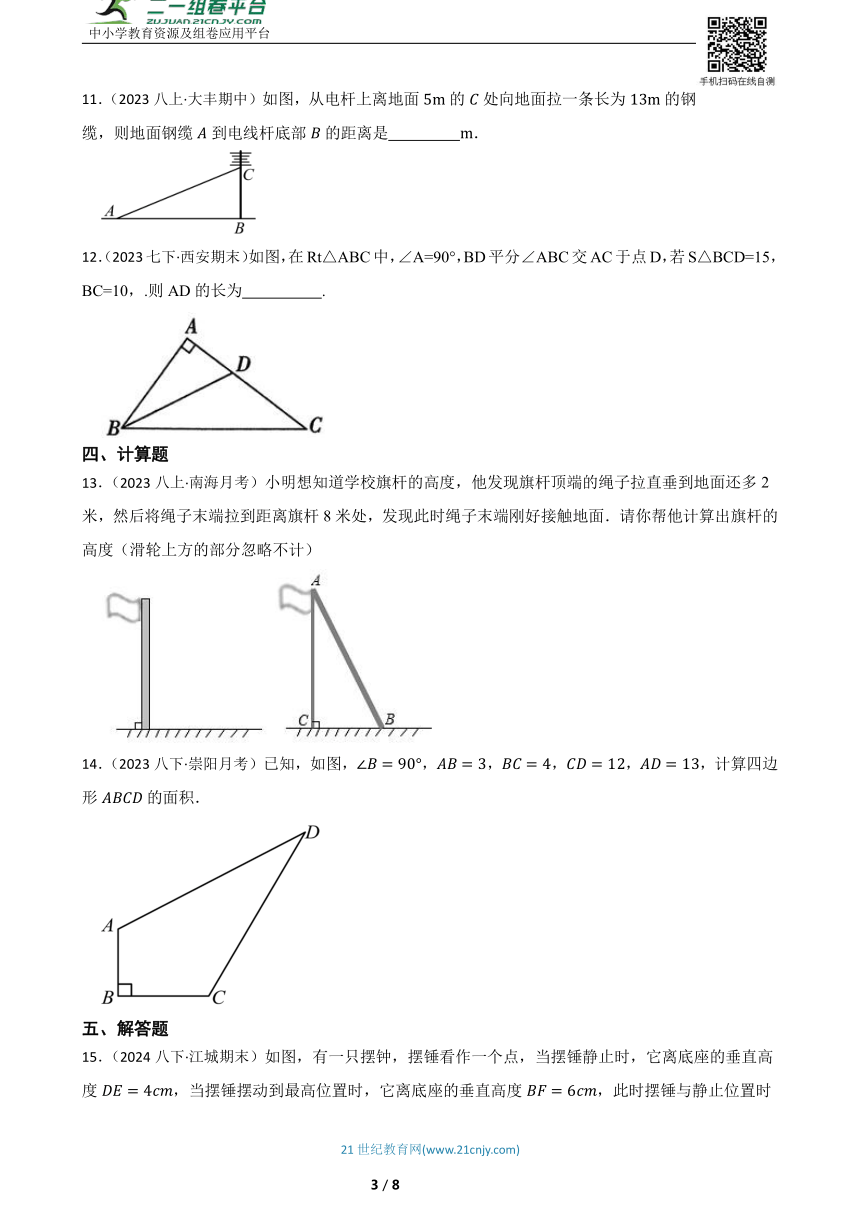
1.(2024八上·兰州期末)如图,小明用的木棒加固小树,已知,,则木棒底端C距树根B之间的距离( )
A. B. C. D.
2.(2023八上·九原月考)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
3.(2024八下·乌鲁木齐期中)以下列各组数为边长,能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.8,9,10 D.13,14,15
4.(2024七上·盐田期末)如图,射线平分,射线平分,则下列等式中成立的有( )
①;②;③;④.
A.①② B.①③ C.②③ D.②④
5.(2024八上·长沙月考)如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,则点到的距离是( )
A.6 B.8 C.10 D.12
二、判断题
6.(2022七上·丰润开学考)判断题:一个直角三角形中,有一个锐角是,另一个锐角是.
三、填空题
7.(2024七上·平潭期末)如图,已知直线,相交于O,平分,,则 .
8.(2024七下·平房期末)在中,为高,直线交于点H,若,则 .
9.(2023八上·冷水滩开学考)如图,是的平分线,,,则的度数为 .
10.(2023八上·南浔期中)一副三角板,按如图所示叠放在一起(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中 度.
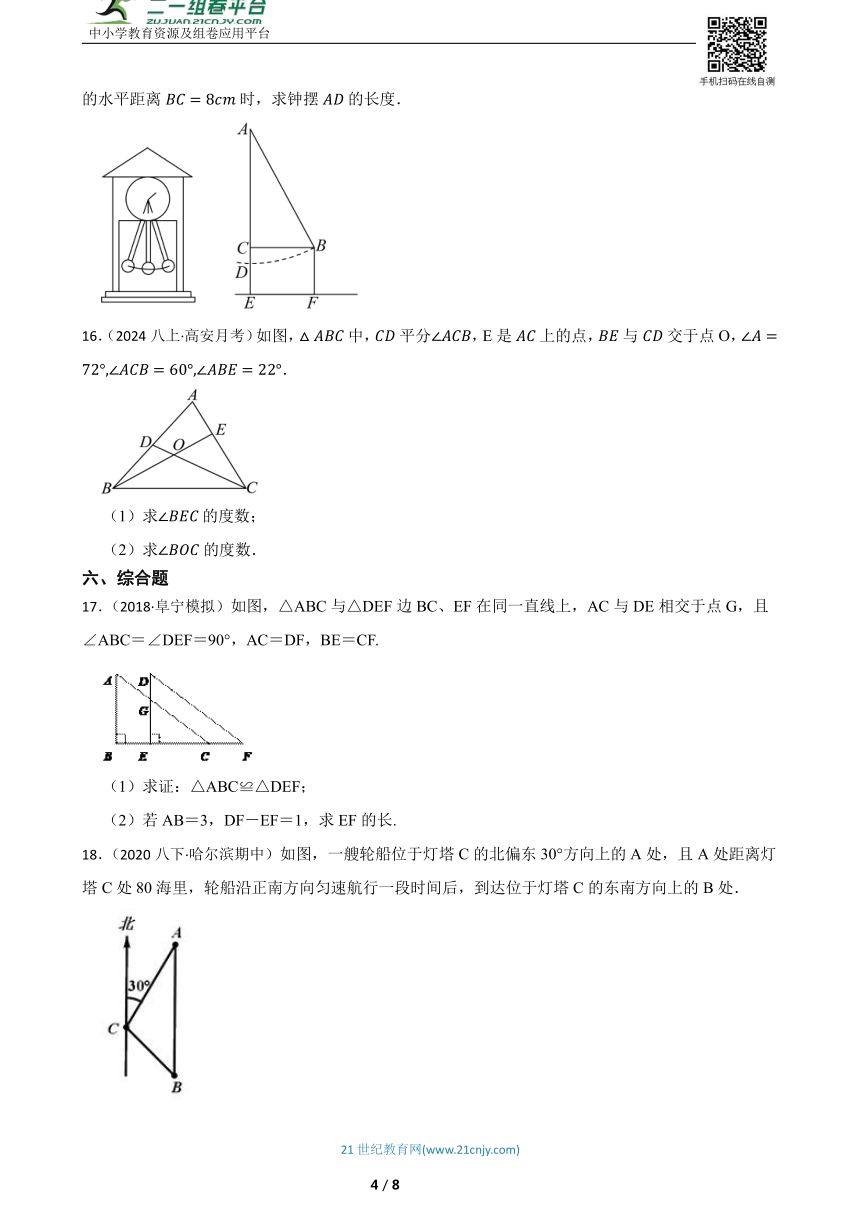
11.(2023八上·大丰期中)如图,从电杆上离地面的处向地面拉一条长为的钢缆,则地面钢缆到电线杆底部的距离是 .
12.(2023七下·西安期末)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,若S△BCD=15,BC=10,.则AD的长为 .
四、计算题
13.(2023八上·南海月考)小明想知道学校旗杆的高度,他发现旗杆顶端的绳子拉直垂到地面还多2米,然后将绳子末端拉到距离旗杆8米处,发现此时绳子末端刚好接触地面.请你帮他计算出旗杆的高度(滑轮上方的部分忽略不计)
14.(2023八下·崇阳月考)已知,如图,,,,,,计算四边形的面积.
五、解答题
15.(2024八下·江城期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度,当摆锤摆动到最高位置时,它离底座的垂直高度,此时摆锤与静止位置时的水平距离时,求钟摆的长度.
16.(2024八上·高安月考)如图,中,平分,E是上的点,与交于点O,.
(1)求的度数;
(2)求的度数.
六、综合题
17.(2018·阜宁模拟)如图,△ABC与△DEF边BC、EF在同一直线上,AC与DE相交于点G,且∠ABC=∠DEF=90°,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)若AB=3,DF-EF=1,求EF的长.
18.(2020八下·哈尔滨期中)如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C处80海里,轮船沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到达航线AB的距离;
(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果保留根号).
19.(2023八上·淮阳期中)如图,在中,,a,b,c分别是,,的对边长,且,,求的面积.
七、实践探究题
20.(2024八下·怀仁期末)某中学计划实施空地绿化工程,负责人王老师将一块四边形空地绿化费用的预算任务交给了“求知”小组,该小组的同学把“空地绿化的合理预算”作为一项课题研究,利用课余时间完成了实践调查报告.
研究课题 空地绿化的合理预算
研究目的 学会运用勾股定理及其逆定理解决生活实际问题
测量工具 测角仪、卷尺
研究方式 走访调研、实地勘察测量
研究方案及测量数据 测量示意图: 相关数据及说明: ①在四边形中,; ②多次测量并求取平均值后的相关长度如图所示; ③测量示意图中代表实际距离; ④每平方米的绿化费用为60元.
计算结果 ……
请根据调查报告,计算绿化这块空地所需的费用.
答案解析部分
1.【答案】A
【知识点】勾股定理;求算术平方根
2.【答案】C
【知识点】勾股定理的逆定理
3.【答案】A
【知识点】勾股定理的逆定理
4.【答案】B
【知识点】角平分线的性质
5.【答案】C
【知识点】角平分线的性质;尺规作图-作角的平分线
6.【答案】正确
【知识点】直角三角形的性质
7.【答案】
【知识点】角平分线的性质;对顶角及其性质
8.【答案】或或
【知识点】三角形的角平分线、中线和高;三角形的外角性质;直角三角形的性质
9.【答案】36°
【知识点】平行线的性质;角平分线的性质
10.【答案】
【知识点】三角形内角和定理;直角三角形的性质;对顶角及其性质
11.【答案】
【知识点】勾股定理
12.【答案】3
【知识点】角平分线的性质
13.【答案】旗杆的高度为15米
【知识点】勾股定理
14.【答案】36
【知识点】勾股定理;勾股定理的逆定理
15.【答案】
【知识点】勾股定理
16.【答案】(1)
(2)
【知识点】三角形的外角性质;角平分线的性质
17.【答案】(1)解:∵BE=CF,∴BC=EF,
在Rt△ABC和Rt△DEF中,
∵AC=DF,BC=EF,
∴△ABC≌△DEF(HL).
(2)解:∵△ABC≌△DEF,
∴ ,
∵ ,
.
【知识点】全等三角形的判定与性质;勾股定理
18.【答案】(1)过点C作CD⊥AB,
由题意可知CN∥AB,∠NCA=30°
∴∠CAB=30°
∴在Rt△ACD中,
答:点C到AB的距离为40海里;
(2)由题意可得:∠MCB=45°
∴在Rt△CDB中,∠DCB=45°
∴DB=CD=40
在Rt△ACD中,
∴AB=AD+DB=
∴轮船从A处到B处所用的时间为 (小时).
【知识点】含30°角的直角三角形;勾股定理的应用
19.【答案】的面积是6
【知识点】勾股定理
20.【答案】绿化这块空地所需的费用为元
【知识点】勾股定理;勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
9 / 9
[专项培优]湘教版数学八年级下册直角三角形
一、单选题
1.(2024八上·兰州期末)如图,小明用的木棒加固小树,已知,,则木棒底端C距树根B之间的距离( )
A. B. C. D.
2.(2023八上·九原月考)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
3.(2024八下·乌鲁木齐期中)以下列各组数为边长,能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.8,9,10 D.13,14,15
4.(2024七上·盐田期末)如图,射线平分,射线平分,则下列等式中成立的有( )
①;②;③;④.
A.①② B.①③ C.②③ D.②④
5.(2024八上·长沙月考)如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,则点到的距离是( )
A.6 B.8 C.10 D.12
二、判断题
6.(2022七上·丰润开学考)判断题:一个直角三角形中,有一个锐角是,另一个锐角是.
三、填空题
7.(2024七上·平潭期末)如图,已知直线,相交于O,平分,,则 .
8.(2024七下·平房期末)在中,为高,直线交于点H,若,则 .
9.(2023八上·冷水滩开学考)如图,是的平分线,,,则的度数为 .
10.(2023八上·南浔期中)一副三角板,按如图所示叠放在一起(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中 度.
11.(2023八上·大丰期中)如图,从电杆上离地面的处向地面拉一条长为的钢缆,则地面钢缆到电线杆底部的距离是 .
12.(2023七下·西安期末)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,若S△BCD=15,BC=10,.则AD的长为 .
四、计算题
13.(2023八上·南海月考)小明想知道学校旗杆的高度,他发现旗杆顶端的绳子拉直垂到地面还多2米,然后将绳子末端拉到距离旗杆8米处,发现此时绳子末端刚好接触地面.请你帮他计算出旗杆的高度(滑轮上方的部分忽略不计)
14.(2023八下·崇阳月考)已知,如图,,,,,,计算四边形的面积.
五、解答题
15.(2024八下·江城期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度,当摆锤摆动到最高位置时,它离底座的垂直高度,此时摆锤与静止位置时的水平距离时,求钟摆的长度.
16.(2024八上·高安月考)如图,中,平分,E是上的点,与交于点O,.
(1)求的度数;
(2)求的度数.
六、综合题
17.(2018·阜宁模拟)如图,△ABC与△DEF边BC、EF在同一直线上,AC与DE相交于点G,且∠ABC=∠DEF=90°,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)若AB=3,DF-EF=1,求EF的长.
18.(2020八下·哈尔滨期中)如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C处80海里,轮船沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到达航线AB的距离;
(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果保留根号).
19.(2023八上·淮阳期中)如图,在中,,a,b,c分别是,,的对边长,且,,求的面积.
七、实践探究题
20.(2024八下·怀仁期末)某中学计划实施空地绿化工程,负责人王老师将一块四边形空地绿化费用的预算任务交给了“求知”小组,该小组的同学把“空地绿化的合理预算”作为一项课题研究,利用课余时间完成了实践调查报告.
研究课题 空地绿化的合理预算
研究目的 学会运用勾股定理及其逆定理解决生活实际问题
测量工具 测角仪、卷尺
研究方式 走访调研、实地勘察测量
研究方案及测量数据 测量示意图: 相关数据及说明: ①在四边形中,; ②多次测量并求取平均值后的相关长度如图所示; ③测量示意图中代表实际距离; ④每平方米的绿化费用为60元.
计算结果 ……
请根据调查报告,计算绿化这块空地所需的费用.
答案解析部分
1.【答案】A
【知识点】勾股定理;求算术平方根
2.【答案】C
【知识点】勾股定理的逆定理
3.【答案】A
【知识点】勾股定理的逆定理
4.【答案】B
【知识点】角平分线的性质
5.【答案】C
【知识点】角平分线的性质;尺规作图-作角的平分线
6.【答案】正确
【知识点】直角三角形的性质
7.【答案】
【知识点】角平分线的性质;对顶角及其性质
8.【答案】或或
【知识点】三角形的角平分线、中线和高;三角形的外角性质;直角三角形的性质
9.【答案】36°
【知识点】平行线的性质;角平分线的性质
10.【答案】
【知识点】三角形内角和定理;直角三角形的性质;对顶角及其性质
11.【答案】
【知识点】勾股定理
12.【答案】3
【知识点】角平分线的性质
13.【答案】旗杆的高度为15米
【知识点】勾股定理
14.【答案】36
【知识点】勾股定理;勾股定理的逆定理
15.【答案】
【知识点】勾股定理
16.【答案】(1)
(2)
【知识点】三角形的外角性质;角平分线的性质
17.【答案】(1)解:∵BE=CF,∴BC=EF,
在Rt△ABC和Rt△DEF中,
∵AC=DF,BC=EF,
∴△ABC≌△DEF(HL).
(2)解:∵△ABC≌△DEF,
∴ ,
∵ ,
.
【知识点】全等三角形的判定与性质;勾股定理
18.【答案】(1)过点C作CD⊥AB,
由题意可知CN∥AB,∠NCA=30°
∴∠CAB=30°
∴在Rt△ACD中,
答:点C到AB的距离为40海里;
(2)由题意可得:∠MCB=45°
∴在Rt△CDB中,∠DCB=45°
∴DB=CD=40
在Rt△ACD中,
∴AB=AD+DB=
∴轮船从A处到B处所用的时间为 (小时).
【知识点】含30°角的直角三角形;勾股定理的应用
19.【答案】的面积是6
【知识点】勾股定理
20.【答案】绿化这块空地所需的费用为元
【知识点】勾股定理;勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
9 / 9
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
