【专项培优】湘教版数学八年级下册第二章四边形(含答案)
文档属性
| 名称 | 【专项培优】湘教版数学八年级下册第二章四边形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【专项培优】湘教版数学八年级下册第二章四边形
一、单选题
1.(2024八下·宝丰期中)下列图形中,是中心对称图形的是( )
A. B. C. D.
2.(2023九上·江油期中)用数学的眼光观察下列图形,是中心对称图形的是( )
A. B.
C. D.
3.(2023九上·监利月考)下列所示国产汽车标识中,可以看作中心对称图形的是( )
A. B.
C. D.
4.下列说法中不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的矩形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的菱形是正方形
5.(2024八下·沙市区期中)如图,平行四边形ABCD中,AB=8,BC=10,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F,且OE=3,则四边形EFCD的周长是( )
A.20 B.24 C.28 D.32
6.(2023九上·郑州经济技术开发月考)如图,四边形的对角线,交于点O,且,,下列说法错误的是( )
A.若,则是菱形
B.若,则是矩形
C.若且,则是正方形
D.若,则是正方形
7.(2024八下·龙马潭月考)如图,在四边形中,,E,F,G分别是的中点,若,则的度数为( )
A. B. C. D.
8.(2025·运城模拟)未来的生活中,AI将扮演非常重要的角色.下列是世界著名人工智能品牌公司的图标,其中是轴对称图形也是中心对称图形的是( )
A. B.
C. D.
9.(2023八下·镇平县期末)如图,在的两边上分别截取使,分别以点A,B为圆心,以的长为半径作弧,两弧交于点C,再连接,若,则四边形的面积是( )
A.240 B.130 C.120 D.65
10.(2022八下·上城期末)已知,是矩形对角线的交点,作,,,相交于点,连结下列说法正确的是( )
四边形为菱形;;;若,则.
A.①③ B.①②④ C.①④ D.③④
二、填空题
11.(2023八下·徐州月考)如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= cm.
12.已知点O为 ABCD两对角线的交点,且S△AOB=1,则S ABCD = .
13.(2023八下·三明期末)如图,在四边形中,厘米,则当 厘米时,四边形是平行四边形.
14.(2024九下·鹿寨开学考)如图,在矩形ABCD中,对角线AC、BD的交点为O,矩形的长、宽分别为7cm、4cm,EF过点O分别交AB、CD于E、F,那么图中阴影部分面积为 cm2.
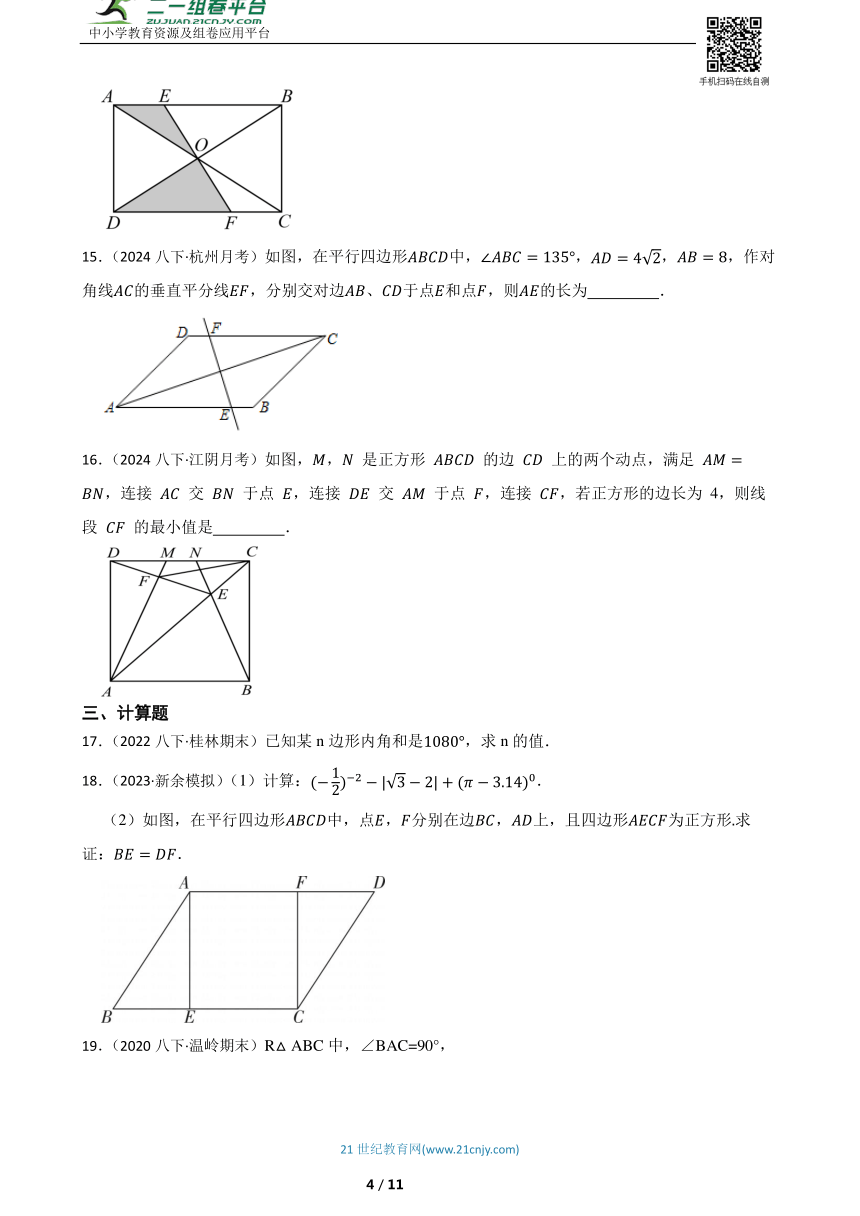
15.(2024八下·杭州月考)如图,在平行四边形中,,,,作对角线的垂直平分线,分别交对边、于点和点,则的长为 .
16.(2024八下·江阴月考)如图,, 是正方形 的边 上的两个动点,满足 ,连接 交 于点 ,连接 交 于点 ,连接 ,若正方形的边长为 4,则线段 的最小值是 .
三、计算题
17.(2022八下·桂林期末)已知某n边形内角和是,求n的值.
18.(2023·新余模拟)(1)计算:.
(2)如图,在平行四边形中,点,分别在边,上,且四边形为正方形求证:.
19.(2020八下·温岭期末)R△ABC中,∠BAC=90°,
(1)如图1,分别以AB、AC、BC为边向外作正方形ABFG、ACPE、BCDE,其面积分别记为S1,S2 ,S3
①若AB=5,AC=12,则S3= ▲ ;
②如图2,将正方形BCDE沿C折, 点D、E的对应点分别记为M、M,若点从M、N分别在直线FG和PH上, 且点M是GO中点时,求S1:S2:S3 ;
③如图3,无论R△ABC三边长度如何变化,点M必定落在直线FG上吗 请说明理由;
(2)如图4,分别以AB, AC, BC为边向外作正三角形ABD, ACF, BCE, 再将三角形BCE沿BC翻折,点E的对应点记为P,若AB= 保持不变,随着AC的长度变化,点P也随之运动,试探究AP的值是否变化,若不变,直接写出AP的值;若改变,直接写出AP的最小值.
四、解答题
20.(2024七下·大丰月考)如果一个多边形的内角和比外角和多,求这个多边形的边数和内角和.
21.(2022九下·温州模拟)如图,矩形的对角线、相交于点,若, 求的度数.
22.(2021九上·秦都期末)如图,菱形ABCD的边长为4, ,以AC为边长作正方形ACEF,求这个正方形的周长.
23. 如图, 在矩形 中, , 菱形 的三个顶点 分别在矩形 的边 上, , 连结 .
(1) 当 时,求证: 四边形 是正方形.
(2) 当 的面积为 2 时,求 的值.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】D
【知识点】中心对称及中心对称图形
3.【答案】C
【知识点】中心对称及中心对称图形
4.【答案】B
【知识点】正方形的判定
5.【答案】B
【知识点】平行四边形的性质
6.【答案】D
【知识点】菱形的判定;矩形的判定与性质;正方形的判定
7.【答案】B
【知识点】三角形内角和定理;等腰三角形的判定与性质;三角形的中位线定理
8.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】C
【知识点】菱形的判定与性质
10.【答案】C
【知识点】直角三角形全等的判定-HL;线段垂直平分线的性质;等边三角形的性质;菱形的判定与性质;矩形的性质
11.【答案】
【知识点】勾股定理;平行四边形的性质
12.【答案】4
【知识点】平行四边形的性质
13.【答案】6
【知识点】平行四边形的判定
14.【答案】7
【知识点】矩形的性质
15.【答案】
【知识点】线段垂直平分线的性质;勾股定理;平行四边形的性质
16.【答案】
【知识点】勾股定理;正方形的判定与性质;三角形全等的判定-SAS;直角三角形斜边上的中线
17.【答案】8
【知识点】多边形内角与外角
18.【答案】(1)解:原式
.
(2)证明:四边形是平行四边形,
,
四边形是正方形,
,
,
,
即.
【知识点】实数的运算;平行四边形的性质;正方形的性质
19.【答案】(1)解:①169
②设正方形ABGF的边长为a,则AB=BF=AG=FG=a,
∵正方形ABGF,正方形AHPC,∠BAC=90°,
∴∠AGO=∠GAH=∠AHO=90°
∴四边形AGOH是矩形,
∴∠F=∠NOM=90°,OG=AH
∵将正方形BCDE沿C折, 点D、E的对应点分别记为M、M
∴BM=MN,∠BMN=90°
∴∠BMF+∠NMO=90°,∠NMO+∠MNO=90°
∴∠BMF=∠MNO
在△BFM和△MON中
∴△BFM≌△MON(AAS)
∴OM=BF=a
∵点G是GO的中点,
∴OG=AH=2OM=2a,
∴正方形AHPC的边长为2a,
AB2+AC2=BC2
∴S12+S22=S32
∴S32=a2+4a2=5a2
∴ S1:S2:S3 =a2:4a2:5a2=1:4:5;
③过点M作MQ⊥HB于点Q,
∵正方形BCNM
∴BM=BC,∠BAC=∠MQB=90°,
∵∠MBQ+∠BMQ=90°,∠MBQ+∠ABC=90°,
∴∠BMQ=∠ABC
在△MBQ和△BCA中
∴△MBQ≌△BCA(AAS)
∴MQ=BA,
∵正方形ABFG,
∴AB=BF=AG,
∴FB=GA=MQ
∵BF∥AG∥MQ
∴点F、G、M三点共线即点M一定落在直线FG上.
(2)AP值会改变,AP最小值为
【知识点】矩形的判定与性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-SAS;三角形全等的判定-AAS
20.【答案】多边形的边数为6,
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
21.【答案】
【知识点】等边三角形的判定与性质;矩形的性质
22.【答案】解:∵四边形ABCD是菱形,∴AB=BC,
∵∠B=60°,∴△ABC是等边三角形,
∴AC=AB=4,∴正方形ACEF的周长是16.
【知识点】等边三角形的判定与性质;菱形的性质;正方形的性质
23.【答案】(1)证明 : ∵四边形ABCD是矩形,
∴
在菱形 中,
,
,
,
,
四边形 是正方形.
(2)解:过 作 于 连结 如图所示,
∵
∴
.
由矩形和菱形性质, 得:
,
,.
,
,
.
,
.
【知识点】菱形的性质;矩形的性质;正方形的判定与性质;三角形全等的判定-AAS
21世纪教育网(www.21cnjy.com)
2 / 11
【专项培优】湘教版数学八年级下册第二章四边形
一、单选题
1.(2024八下·宝丰期中)下列图形中,是中心对称图形的是( )
A. B. C. D.
2.(2023九上·江油期中)用数学的眼光观察下列图形,是中心对称图形的是( )
A. B.
C. D.
3.(2023九上·监利月考)下列所示国产汽车标识中,可以看作中心对称图形的是( )
A. B.
C. D.
4.下列说法中不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的矩形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的菱形是正方形
5.(2024八下·沙市区期中)如图,平行四边形ABCD中,AB=8,BC=10,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F,且OE=3,则四边形EFCD的周长是( )
A.20 B.24 C.28 D.32
6.(2023九上·郑州经济技术开发月考)如图,四边形的对角线,交于点O,且,,下列说法错误的是( )
A.若,则是菱形
B.若,则是矩形
C.若且,则是正方形
D.若,则是正方形
7.(2024八下·龙马潭月考)如图,在四边形中,,E,F,G分别是的中点,若,则的度数为( )
A. B. C. D.
8.(2025·运城模拟)未来的生活中,AI将扮演非常重要的角色.下列是世界著名人工智能品牌公司的图标,其中是轴对称图形也是中心对称图形的是( )
A. B.
C. D.
9.(2023八下·镇平县期末)如图,在的两边上分别截取使,分别以点A,B为圆心,以的长为半径作弧,两弧交于点C,再连接,若,则四边形的面积是( )
A.240 B.130 C.120 D.65
10.(2022八下·上城期末)已知,是矩形对角线的交点,作,,,相交于点,连结下列说法正确的是( )
四边形为菱形;;;若,则.
A.①③ B.①②④ C.①④ D.③④
二、填空题
11.(2023八下·徐州月考)如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= cm.
12.已知点O为 ABCD两对角线的交点,且S△AOB=1,则S ABCD = .
13.(2023八下·三明期末)如图,在四边形中,厘米,则当 厘米时,四边形是平行四边形.
14.(2024九下·鹿寨开学考)如图,在矩形ABCD中,对角线AC、BD的交点为O,矩形的长、宽分别为7cm、4cm,EF过点O分别交AB、CD于E、F,那么图中阴影部分面积为 cm2.
15.(2024八下·杭州月考)如图,在平行四边形中,,,,作对角线的垂直平分线,分别交对边、于点和点,则的长为 .
16.(2024八下·江阴月考)如图,, 是正方形 的边 上的两个动点,满足 ,连接 交 于点 ,连接 交 于点 ,连接 ,若正方形的边长为 4,则线段 的最小值是 .
三、计算题
17.(2022八下·桂林期末)已知某n边形内角和是,求n的值.
18.(2023·新余模拟)(1)计算:.
(2)如图,在平行四边形中,点,分别在边,上,且四边形为正方形求证:.
19.(2020八下·温岭期末)R△ABC中,∠BAC=90°,
(1)如图1,分别以AB、AC、BC为边向外作正方形ABFG、ACPE、BCDE,其面积分别记为S1,S2 ,S3
①若AB=5,AC=12,则S3= ▲ ;
②如图2,将正方形BCDE沿C折, 点D、E的对应点分别记为M、M,若点从M、N分别在直线FG和PH上, 且点M是GO中点时,求S1:S2:S3 ;
③如图3,无论R△ABC三边长度如何变化,点M必定落在直线FG上吗 请说明理由;
(2)如图4,分别以AB, AC, BC为边向外作正三角形ABD, ACF, BCE, 再将三角形BCE沿BC翻折,点E的对应点记为P,若AB= 保持不变,随着AC的长度变化,点P也随之运动,试探究AP的值是否变化,若不变,直接写出AP的值;若改变,直接写出AP的最小值.
四、解答题
20.(2024七下·大丰月考)如果一个多边形的内角和比外角和多,求这个多边形的边数和内角和.
21.(2022九下·温州模拟)如图,矩形的对角线、相交于点,若, 求的度数.
22.(2021九上·秦都期末)如图,菱形ABCD的边长为4, ,以AC为边长作正方形ACEF,求这个正方形的周长.
23. 如图, 在矩形 中, , 菱形 的三个顶点 分别在矩形 的边 上, , 连结 .
(1) 当 时,求证: 四边形 是正方形.
(2) 当 的面积为 2 时,求 的值.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】D
【知识点】中心对称及中心对称图形
3.【答案】C
【知识点】中心对称及中心对称图形
4.【答案】B
【知识点】正方形的判定
5.【答案】B
【知识点】平行四边形的性质
6.【答案】D
【知识点】菱形的判定;矩形的判定与性质;正方形的判定
7.【答案】B
【知识点】三角形内角和定理;等腰三角形的判定与性质;三角形的中位线定理
8.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】C
【知识点】菱形的判定与性质
10.【答案】C
【知识点】直角三角形全等的判定-HL;线段垂直平分线的性质;等边三角形的性质;菱形的判定与性质;矩形的性质
11.【答案】
【知识点】勾股定理;平行四边形的性质
12.【答案】4
【知识点】平行四边形的性质
13.【答案】6
【知识点】平行四边形的判定
14.【答案】7
【知识点】矩形的性质
15.【答案】
【知识点】线段垂直平分线的性质;勾股定理;平行四边形的性质
16.【答案】
【知识点】勾股定理;正方形的判定与性质;三角形全等的判定-SAS;直角三角形斜边上的中线
17.【答案】8
【知识点】多边形内角与外角
18.【答案】(1)解:原式
.
(2)证明:四边形是平行四边形,
,
四边形是正方形,
,
,
,
即.
【知识点】实数的运算;平行四边形的性质;正方形的性质
19.【答案】(1)解:①169
②设正方形ABGF的边长为a,则AB=BF=AG=FG=a,
∵正方形ABGF,正方形AHPC,∠BAC=90°,
∴∠AGO=∠GAH=∠AHO=90°
∴四边形AGOH是矩形,
∴∠F=∠NOM=90°,OG=AH
∵将正方形BCDE沿C折, 点D、E的对应点分别记为M、M
∴BM=MN,∠BMN=90°
∴∠BMF+∠NMO=90°,∠NMO+∠MNO=90°
∴∠BMF=∠MNO
在△BFM和△MON中
∴△BFM≌△MON(AAS)
∴OM=BF=a
∵点G是GO的中点,
∴OG=AH=2OM=2a,
∴正方形AHPC的边长为2a,
AB2+AC2=BC2
∴S12+S22=S32
∴S32=a2+4a2=5a2
∴ S1:S2:S3 =a2:4a2:5a2=1:4:5;
③过点M作MQ⊥HB于点Q,
∵正方形BCNM
∴BM=BC,∠BAC=∠MQB=90°,
∵∠MBQ+∠BMQ=90°,∠MBQ+∠ABC=90°,
∴∠BMQ=∠ABC
在△MBQ和△BCA中
∴△MBQ≌△BCA(AAS)
∴MQ=BA,
∵正方形ABFG,
∴AB=BF=AG,
∴FB=GA=MQ
∵BF∥AG∥MQ
∴点F、G、M三点共线即点M一定落在直线FG上.
(2)AP值会改变,AP最小值为
【知识点】矩形的判定与性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-SAS;三角形全等的判定-AAS
20.【答案】多边形的边数为6,
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
21.【答案】
【知识点】等边三角形的判定与性质;矩形的性质
22.【答案】解:∵四边形ABCD是菱形,∴AB=BC,
∵∠B=60°,∴△ABC是等边三角形,
∴AC=AB=4,∴正方形ACEF的周长是16.
【知识点】等边三角形的判定与性质;菱形的性质;正方形的性质
23.【答案】(1)证明 : ∵四边形ABCD是矩形,
∴
在菱形 中,
,
,
,
,
四边形 是正方形.
(2)解:过 作 于 连结 如图所示,
∵
∴
.
由矩形和菱形性质, 得:
,
,.
,
,
.
,
.
【知识点】菱形的性质;矩形的性质;正方形的判定与性质;三角形全等的判定-AAS
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
