【专项培优】湘教版数学八年级下册第三章图形与坐标(含答案)
文档属性
| 名称 | 【专项培优】湘教版数学八年级下册第三章图形与坐标(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【专项培优】湘教版数学八年级下册第三章图形与坐标
一、单选题
1.(2023八下·桥西期末)如图是象棋棋盘的一部分,若“相”位于点上,“帅”位于点上,则“兵”的坐标为( )
A. B. C. D.
2.(2023九上·南召期中)如图,与关于点成中心对称,若点A的坐标为,则点的坐标为( )
A. B. C. D.
3.(2024七下·浦城期中)下列语句正确的是( )
A.a的平方根是(a≥0)
B.在同一平面内,垂直于同一条直线的两直线平行
C.同旁内角互补
D.若ab=0,则点P(a,b)在坐标原点
4.(2023八上·汕头期中)如图,在平面直角坐标系中,已知点的坐标是,以为边在右侧作等边三角形,过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,再过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,…,按此规律继续作下去,得到等边三角形,则点的纵坐标为( )
A. B. C. D.
5.(2023七下·鹿泉期中)一个正方形在平面直角坐标系中三个顶点的坐标为、、,则第四个顶点的坐标为( )
A. B. C. D.
6.(2020·金华模拟)如图,在一单位为1的方格纸上, , , …,都是斜边在 轴上,斜边长分别为2,4,6,…的等腰直角三角形,若 的顶点坐标分别为 , , ,则依图中所示规律, 的坐标为( )
A. B. C. D.
7.与点A(-1,2)关于y轴对称的点是点B,则点B的坐标是( )
A.(1,-2) B.(-1,-2) C.(1,2) D.(2,1)
8.(2023七下·林州期末)在平面直角坐标系中,对于点P,我们把点叫做点P的伴随点.已知点的伴随点为点,的伴随点为,点的伴随点为,….若点的坐标为,则点的坐标为( )
A. B. C. D.
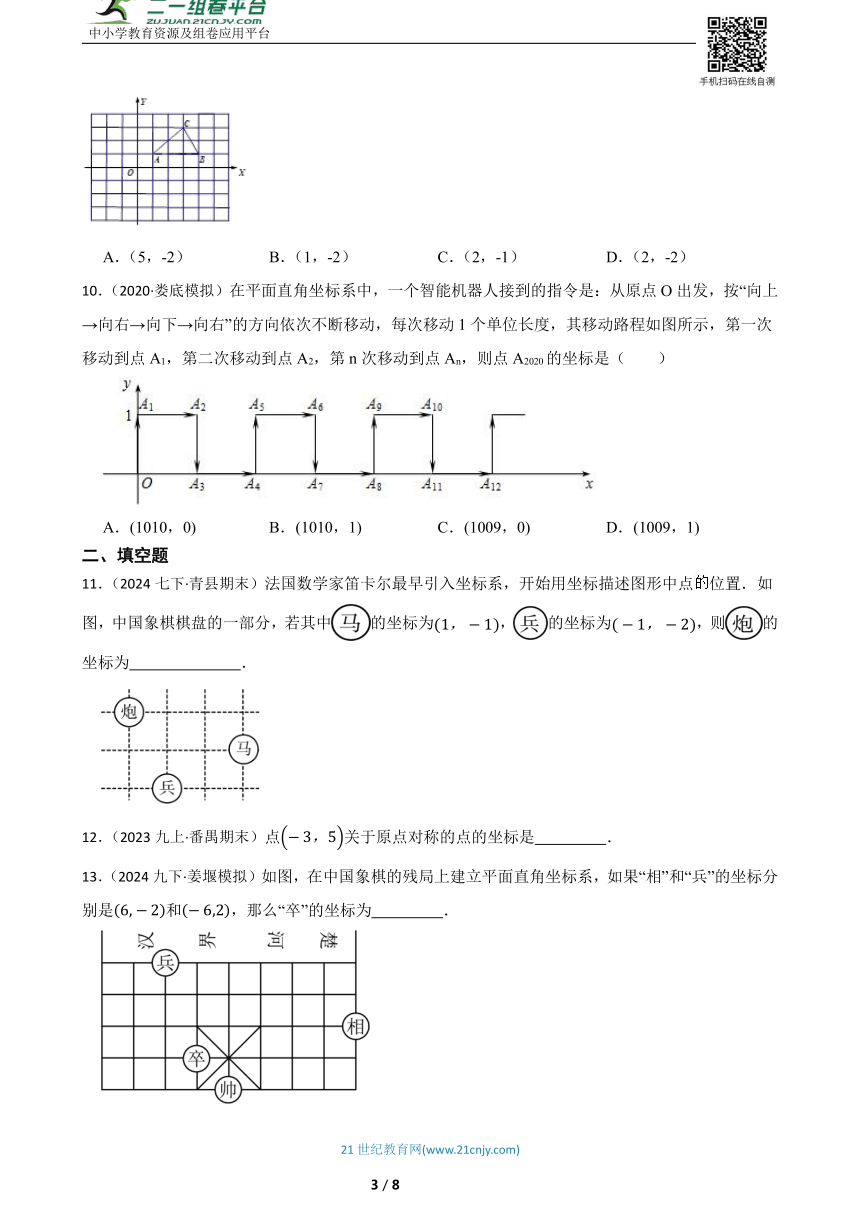
9.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,平移后C点的坐标是( )
A.(5,-2) B.(1,-2) C.(2,-1) D.(2,-2)
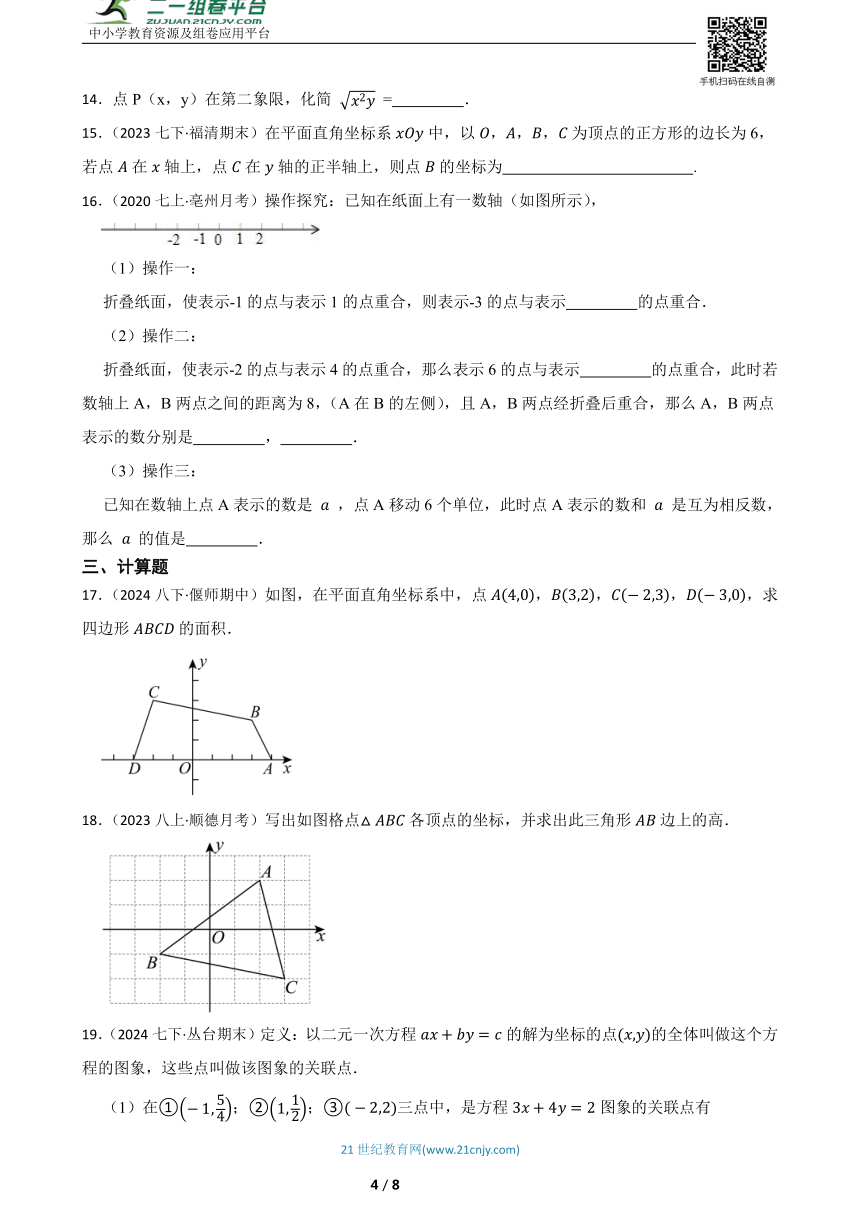
10.(2020·娄底模拟)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路程如图所示,第一次移动到点A1,第二次移动到点A2,第n次移动到点An,则点A2020的坐标是( )
A.(1010,0) B.(1010,1) C.(1009,0) D.(1009,1)
二、填空题
11.(2024七下·青县期末)法国数学家笛卡尔最早引入坐标系,开始用坐标描述图形中点位置.如图,中国象棋棋盘的一部分,若其中的坐标为,的坐标为,则的坐标为 .
12.(2023九上·番禺期末)点关于原点对称的点的坐标是 .
13.(2024九下·姜堰模拟)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是和,那么“卒”的坐标为 .
14.点P(x,y)在第二象限,化简 = .
15.(2023七下·福清期末)在平面直角坐标系中,以,,,为顶点的正方形的边长为6,若点在轴上,点在轴的正半轴上,则点的坐标为 .
16.(2020七上·亳州月考)操作探究:已知在纸面上有一数轴(如图所示),
(1)操作一:
折叠纸面,使表示-1的点与表示1的点重合,则表示-3的点与表示 的点重合.
(2)操作二:
折叠纸面,使表示-2的点与表示4的点重合,那么表示6的点与表示 的点重合,此时若数轴上A,B两点之间的距离为8,(A在B的左侧),且A,B两点经折叠后重合,那么A,B两点表示的数分别是 , .
(3)操作三:
已知在数轴上点A表示的数是 ,点A移动6个单位,此时点A表示的数和 是互为相反数,那么 的值是 .
三、计算题
17.(2024八下·偃师期中)如图,在平面直角坐标系中,点,,,,求四边形的面积.
18.(2023八上·顺德月考)写出如图格点各顶点的坐标,并求出此三角形边上的高.
19.(2024七下·丛台期末)定义:以二元一次方程的解为坐标的点的全体叫做这个方程的图象,这些点叫做该图象的关联点.
(1)在①;②;③三点中,是方程图象的关联点有______________;(填序号)
(2)已知A,C两点是方程图象的关联点,B,C两点是方程图象的关联点.若点A在x轴上,点B在y轴上,求四边形的面积.
(3)若,,三点是二元一次方程图象的关联点,探究m,n,p,q之间的关系,请直接写出你的结论.
四、解答题
20.(2023七下·武汉期中)已知平面直角坐标系中有一点.
(1)若点且轴时,求M的坐标;
(2)若点M在y轴的右边,且到y轴的距离为3时,求M的坐标.
21.(2024八上·柳州期末)已知点.
(1)若点与点的连线与轴平行,求点的坐标.
(2)若的平方根是,直线经过点,求的值.
22.(2024七下·红塔期中) 当点的坐标满足时,称点为“倒立点”.
(1)判断点 “倒立点”;点 “倒立点”;(填“是”或者“不是”)
(2)如果点是倒立点,那么点是倒立点吗?请说明理由.
(3)已知点是倒立点,,轴,且,求点的坐标.
23.(2023八上·咸丰月考)如图,在平面直角坐标系中,的顶点、在轴上,点在轴上,点,点,且、满足,.
(1)求的面积;
(2)动点从点出发,沿向终点以每秒2个单位的速度运动,连接过点作的垂线,垂足为,交轴于点,设点的运动时间为秒,的面积为,请你用含的式子表示;
(3)在(2)的条件下,,当是以为腰的等腰三角形时,求的面积.
答案解析部分
1.【答案】A
【知识点】用坐标表示地理位置
2.【答案】D
【知识点】关于原点对称的点的坐标特征
3.【答案】B
【知识点】点的坐标;平行线的判定;平行线的性质;有理数的乘法法则;平方根的概念与表示
4.【答案】B
【知识点】点的坐标;坐标与图形性质;等边三角形的性质;含30°角的直角三角形
5.【答案】A
【知识点】点的坐标
6.【答案】D
【知识点】坐标与图形性质;探索图形规律
7.【答案】C
【知识点】关于坐标轴对称的点的坐标特征
8.【答案】B
【知识点】点的坐标
9.【答案】B
【知识点】坐标与图形变化﹣平移
10.【答案】A
【知识点】点的坐标
11.【答案】
【知识点】用坐标表示地理位置
12.【答案】
【知识点】关于原点对称的点的坐标特征
13.【答案】
【知识点】用坐标表示地理位置
14.【答案】﹣x
【知识点】二次根式的性质与化简;点的坐标
15.【答案】(6,6)或(-6,6)
【知识点】坐标与图形性质;正方形的性质
16.【答案】(1)3
(2)-4;-3;5
(3)3或-3
【知识点】数轴及有理数在数轴上的表示;翻折变换(折叠问题);坐标与图形变化﹣平移
17.【答案】15
【知识点】坐标与图形性质
18.【答案】,
【知识点】坐标与图形性质;三角形的角平分线、中线和高;三角形的面积;勾股定理
19.【答案】(1)①③;
(2);
(3).
【知识点】二元一次方程的解;解二元一次方程组;坐标与图形性质
20.【答案】(1)
(2)
【知识点】点的坐标;坐标与图形性质
21.【答案】(1)
(2)1
【知识点】点的坐标;平方根的概念与表示
22.【答案】(1)不是;是
(2)解:点是倒立点,理由如下,
∵点是倒立点,
∴
即
∴点是倒立点,
(3)解:∵点是倒立点,
∴
∵,轴,
∴,
∵,
∴
∴或
当时,,
当,时,
∴
【知识点】坐标与图形性质
23.【答案】(1)
(2)
(3)或
【知识点】坐标与图形性质;等腰三角形的判定与性质;绝对值的非负性
21世纪教育网(www.21cnjy.com)
1 / 8
【专项培优】湘教版数学八年级下册第三章图形与坐标
一、单选题
1.(2023八下·桥西期末)如图是象棋棋盘的一部分,若“相”位于点上,“帅”位于点上,则“兵”的坐标为( )
A. B. C. D.
2.(2023九上·南召期中)如图,与关于点成中心对称,若点A的坐标为,则点的坐标为( )
A. B. C. D.
3.(2024七下·浦城期中)下列语句正确的是( )
A.a的平方根是(a≥0)
B.在同一平面内,垂直于同一条直线的两直线平行
C.同旁内角互补
D.若ab=0,则点P(a,b)在坐标原点
4.(2023八上·汕头期中)如图,在平面直角坐标系中,已知点的坐标是,以为边在右侧作等边三角形,过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,再过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,…,按此规律继续作下去,得到等边三角形,则点的纵坐标为( )
A. B. C. D.
5.(2023七下·鹿泉期中)一个正方形在平面直角坐标系中三个顶点的坐标为、、,则第四个顶点的坐标为( )
A. B. C. D.
6.(2020·金华模拟)如图,在一单位为1的方格纸上, , , …,都是斜边在 轴上,斜边长分别为2,4,6,…的等腰直角三角形,若 的顶点坐标分别为 , , ,则依图中所示规律, 的坐标为( )
A. B. C. D.
7.与点A(-1,2)关于y轴对称的点是点B,则点B的坐标是( )
A.(1,-2) B.(-1,-2) C.(1,2) D.(2,1)
8.(2023七下·林州期末)在平面直角坐标系中,对于点P,我们把点叫做点P的伴随点.已知点的伴随点为点,的伴随点为,点的伴随点为,….若点的坐标为,则点的坐标为( )
A. B. C. D.
9.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,平移后C点的坐标是( )
A.(5,-2) B.(1,-2) C.(2,-1) D.(2,-2)
10.(2020·娄底模拟)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路程如图所示,第一次移动到点A1,第二次移动到点A2,第n次移动到点An,则点A2020的坐标是( )
A.(1010,0) B.(1010,1) C.(1009,0) D.(1009,1)
二、填空题
11.(2024七下·青县期末)法国数学家笛卡尔最早引入坐标系,开始用坐标描述图形中点位置.如图,中国象棋棋盘的一部分,若其中的坐标为,的坐标为,则的坐标为 .
12.(2023九上·番禺期末)点关于原点对称的点的坐标是 .
13.(2024九下·姜堰模拟)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是和,那么“卒”的坐标为 .
14.点P(x,y)在第二象限,化简 = .
15.(2023七下·福清期末)在平面直角坐标系中,以,,,为顶点的正方形的边长为6,若点在轴上,点在轴的正半轴上,则点的坐标为 .
16.(2020七上·亳州月考)操作探究:已知在纸面上有一数轴(如图所示),
(1)操作一:
折叠纸面,使表示-1的点与表示1的点重合,则表示-3的点与表示 的点重合.
(2)操作二:
折叠纸面,使表示-2的点与表示4的点重合,那么表示6的点与表示 的点重合,此时若数轴上A,B两点之间的距离为8,(A在B的左侧),且A,B两点经折叠后重合,那么A,B两点表示的数分别是 , .
(3)操作三:
已知在数轴上点A表示的数是 ,点A移动6个单位,此时点A表示的数和 是互为相反数,那么 的值是 .
三、计算题
17.(2024八下·偃师期中)如图,在平面直角坐标系中,点,,,,求四边形的面积.
18.(2023八上·顺德月考)写出如图格点各顶点的坐标,并求出此三角形边上的高.
19.(2024七下·丛台期末)定义:以二元一次方程的解为坐标的点的全体叫做这个方程的图象,这些点叫做该图象的关联点.
(1)在①;②;③三点中,是方程图象的关联点有______________;(填序号)
(2)已知A,C两点是方程图象的关联点,B,C两点是方程图象的关联点.若点A在x轴上,点B在y轴上,求四边形的面积.
(3)若,,三点是二元一次方程图象的关联点,探究m,n,p,q之间的关系,请直接写出你的结论.
四、解答题
20.(2023七下·武汉期中)已知平面直角坐标系中有一点.
(1)若点且轴时,求M的坐标;
(2)若点M在y轴的右边,且到y轴的距离为3时,求M的坐标.
21.(2024八上·柳州期末)已知点.
(1)若点与点的连线与轴平行,求点的坐标.
(2)若的平方根是,直线经过点,求的值.
22.(2024七下·红塔期中) 当点的坐标满足时,称点为“倒立点”.
(1)判断点 “倒立点”;点 “倒立点”;(填“是”或者“不是”)
(2)如果点是倒立点,那么点是倒立点吗?请说明理由.
(3)已知点是倒立点,,轴,且,求点的坐标.
23.(2023八上·咸丰月考)如图,在平面直角坐标系中,的顶点、在轴上,点在轴上,点,点,且、满足,.
(1)求的面积;
(2)动点从点出发,沿向终点以每秒2个单位的速度运动,连接过点作的垂线,垂足为,交轴于点,设点的运动时间为秒,的面积为,请你用含的式子表示;
(3)在(2)的条件下,,当是以为腰的等腰三角形时,求的面积.
答案解析部分
1.【答案】A
【知识点】用坐标表示地理位置
2.【答案】D
【知识点】关于原点对称的点的坐标特征
3.【答案】B
【知识点】点的坐标;平行线的判定;平行线的性质;有理数的乘法法则;平方根的概念与表示
4.【答案】B
【知识点】点的坐标;坐标与图形性质;等边三角形的性质;含30°角的直角三角形
5.【答案】A
【知识点】点的坐标
6.【答案】D
【知识点】坐标与图形性质;探索图形规律
7.【答案】C
【知识点】关于坐标轴对称的点的坐标特征
8.【答案】B
【知识点】点的坐标
9.【答案】B
【知识点】坐标与图形变化﹣平移
10.【答案】A
【知识点】点的坐标
11.【答案】
【知识点】用坐标表示地理位置
12.【答案】
【知识点】关于原点对称的点的坐标特征
13.【答案】
【知识点】用坐标表示地理位置
14.【答案】﹣x
【知识点】二次根式的性质与化简;点的坐标
15.【答案】(6,6)或(-6,6)
【知识点】坐标与图形性质;正方形的性质
16.【答案】(1)3
(2)-4;-3;5
(3)3或-3
【知识点】数轴及有理数在数轴上的表示;翻折变换(折叠问题);坐标与图形变化﹣平移
17.【答案】15
【知识点】坐标与图形性质
18.【答案】,
【知识点】坐标与图形性质;三角形的角平分线、中线和高;三角形的面积;勾股定理
19.【答案】(1)①③;
(2);
(3).
【知识点】二元一次方程的解;解二元一次方程组;坐标与图形性质
20.【答案】(1)
(2)
【知识点】点的坐标;坐标与图形性质
21.【答案】(1)
(2)1
【知识点】点的坐标;平方根的概念与表示
22.【答案】(1)不是;是
(2)解:点是倒立点,理由如下,
∵点是倒立点,
∴
即
∴点是倒立点,
(3)解:∵点是倒立点,
∴
∵,轴,
∴,
∵,
∴
∴或
当时,,
当,时,
∴
【知识点】坐标与图形性质
23.【答案】(1)
(2)
(3)或
【知识点】坐标与图形性质;等腰三角形的判定与性质;绝对值的非负性
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
