【专项培优】湘教版数学八年级下册第四章一次函数(含答案)
文档属性
| 名称 | 【专项培优】湘教版数学八年级下册第四章一次函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【专项培优】湘教版数学八年级下册第四章一次函数
一、单选题
1.(2023八下·泸县月考)对于一次函数 y = kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,
x -1 0 1 3
y 7 5 2 -1
其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A.-1 B.2 C.5 D.7
2.(2023八上·海州期中)下列函数:①;②;③;④,其中一次函数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2024九上·南皮月考)关于的一元二次方程的根的情况,叙述正确的是( )
A.方程没有实数根
B.方程有两个实数根
C.若直线不经过第三象限,则方程有两个不相等的实数根
D.若直线不经过第一象限,则方程有两个不相等的实数根
4.(2019八上·永登期末)一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( )
A.-2 B.2 C.1 D.-2或2
5.(2023六下·岱岳期末)在某一阶段,某商品的销售量y与销售价x之间存在如表关系:
销售价x/元 90 100 110 120 130 140
销售量y/件 90 80 70 60 50 40
以下结论错误的是( )
A.当时, B.当时,
C.当时, D.当时,
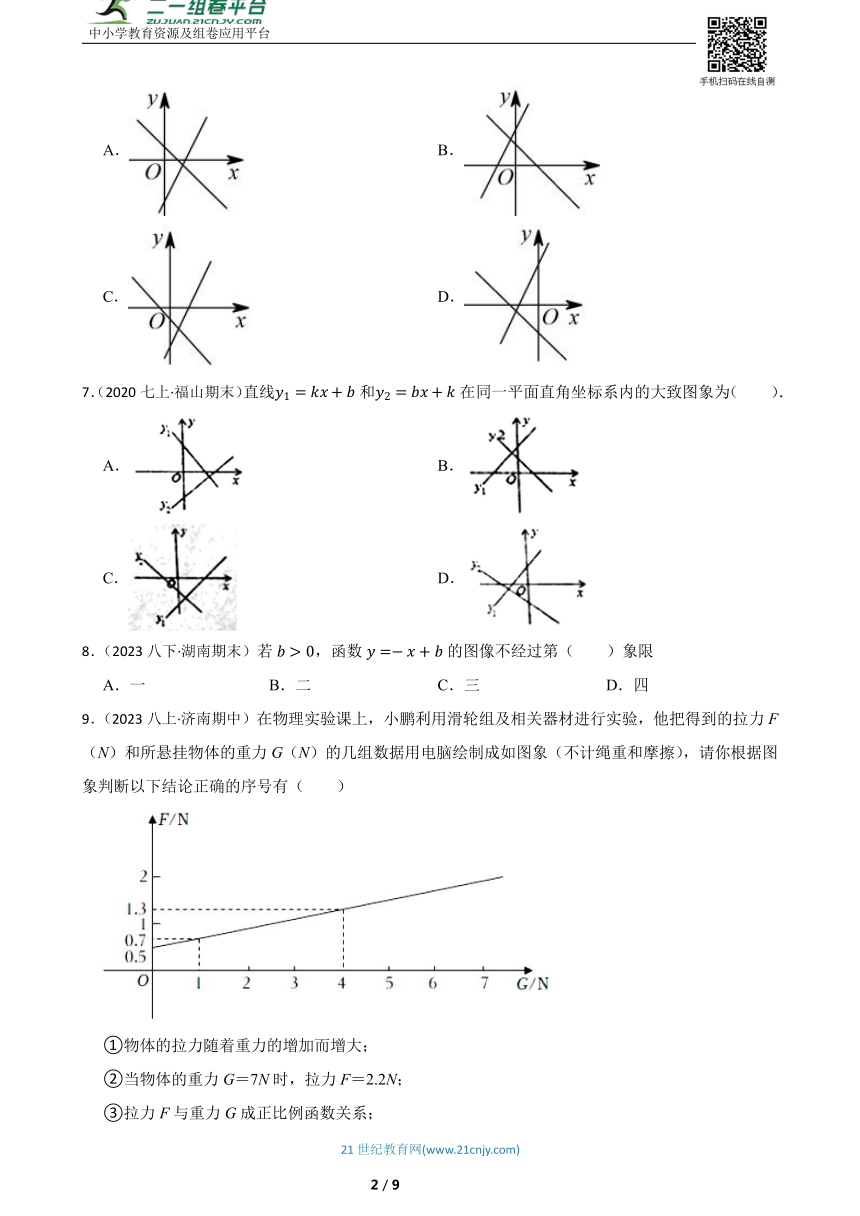
6.(2021八下·台州期中)直线y=kx+b和y=bx+k在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
7.(2020七上·福山期末)直线和在同一平面直角坐标系内的大致图象为( ).
A. B.
C. D.
8.(2023八下·湖南期末)若,函数的图像不经过第( )象限
A.一 B.二 C.三 D.四
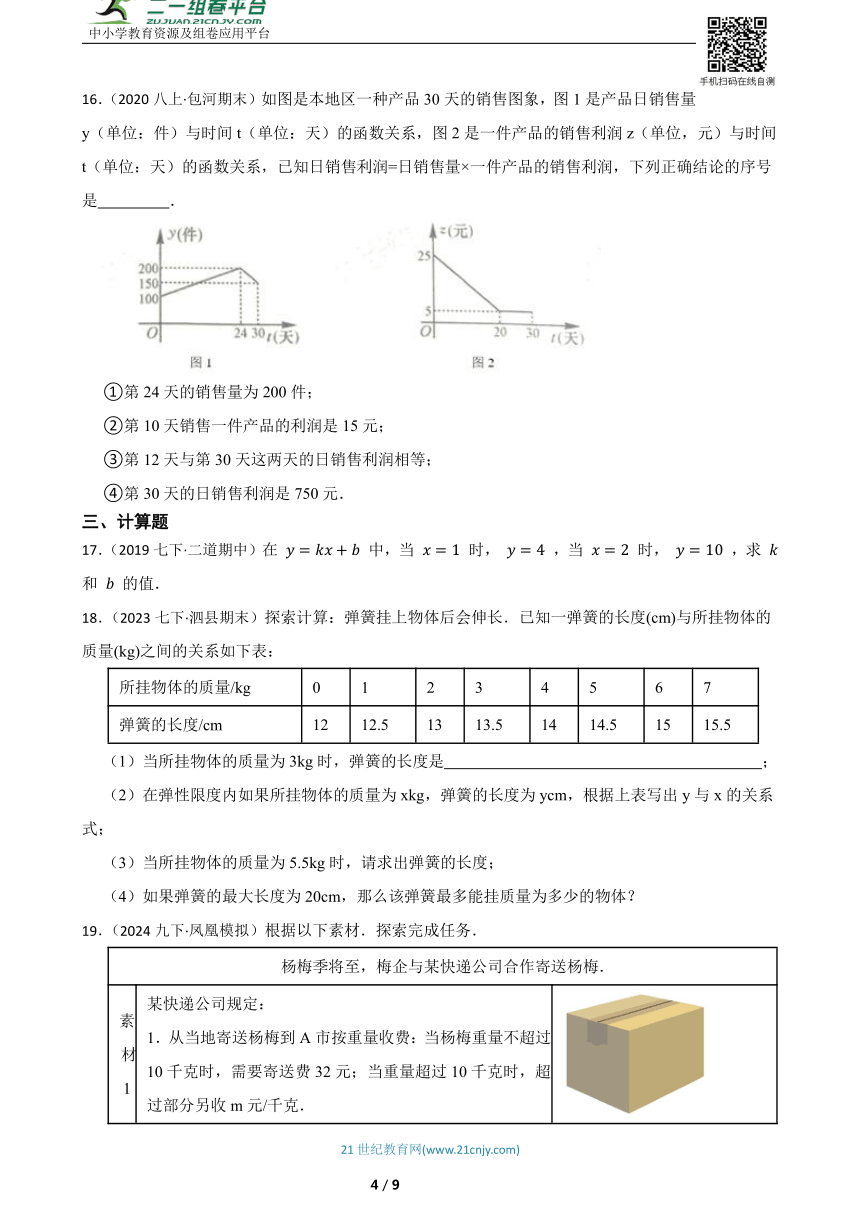
9.(2023八上·济南期中)在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7N时,拉力F=2.2N;
③拉力F与重力G成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N.
A.①② B.②④ C.①④ D.③④
10.(2023九上·东平月考)学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要
B.水温下降过程中,y与x的函数关系式是
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.水温不低于30℃的时间为
二、填空题
11.(2021九下·浦东期中)已知正比例函数,那么y的值随x的值增大而 (填“增大或“减小”)
12.(2021八下·武进月考)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
13.(2017八下·宣城期末)直线y= 不经过第 象限,y随x的增大而 .
14.(2024七下·榕城期末)王大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为米,要围成的菜园是如图所示的长方形,设边的长为米,边的长为米,则与的关系式是 .
15.(2024八上·沅江开学考)已知关于的分式方程有整数解,且一次函数图象经过第一、二、三象限,则整数的值为 .
16.(2020八上·包河期末)如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是 .
①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
三、计算题
17.(2019七下·二道期中)在 中,当 时, ,当 时, ,求 和 的值.
18.(2023七下·泗县期末)探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3kg时,弹簧的长度是 ;
(2)在弹性限度内如果所挂物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20cm,那么该弹簧最多能挂质量为多少的物体?
19.(2024九下·凤凰模拟)根据以下素材.探索完成任务.
杨梅季将至,梅企与某快递公司合作寄送杨梅.
素材1 某快递公司规定: 1.从当地寄送杨梅到A市按重量收费:当杨梅重量不超过10千克时,需要寄送费32元;当重量超过10千克时,超过部分另收m元/千克. 2.寄送杨梅重量均为整数千克.
素材2 电子存单1托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:7千克 件数:1 总费用:32元
电子存单2托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:12千克 件数:1 总费用:44元
电子存单3托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:15千克 件数:1 总费用:62元
问题解决
任务1 分析变量关系 根据以上信息,请确定m的值,并求出杨梅重量超过10千克时寄送费用y(元)关于杨梅重量x(千克)之间的函数关系式.
任务2 计算最省费用 若杨梅重量达到25千克,请求出最省的寄送费用.
任务3 探索最大重量 小聪想在当地梅企购买一批价格为50元/千克的杨梅并全部寄送给在A市的朋友们,若小聪能用来支配的钱有5000元,他最多可以购买多少千克的杨梅?并写出一种寄送方式.
四、解答题
20.(2022七下·成都期末)周末,小明和爸爸从家出发去青龙湖公园露营,早上9:00小明徒步先行出发,爸爸带上露营物资骑自行车后出发,到达露营地扎营.行进过程中爸爸和小明行驶速度均保持不变,两人离家的距离与时间如图所示.请根据图象回答问题:
(1)爸爸比小明晚出发_____min:小明徒步的速度是_____km/min﹔爸爸骑自行车的速度是____km/min;
(2)爸爸比小明早多久到达营地
21.(2024八下·福州期中)已知与成正比例,且时.
(1)求y与x之间的函数关系式;
(2)由(1)得到的函数图象上有一点P到x轴的距离为4,求点P坐标.
22.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤30)
提出概念所 用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59.0 59.8 59.9 59.8 58.3 55.0
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用时间是5分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(4)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
23.(2024八下·济南期末)如图1,在平面直角坐标系中,一次函数的图象分别交轴,轴于,两点,将绕点顺时针旋转得(点与点对应,点与点对应).
(1)直接写出直线的解析式;
(2)点为线段上一点,过点作轴交直线于点,作轴交直线于点,当时,求点的坐标;
(3)如图,若点为线段的中点,点为直线上一点,点为坐标系内一点.且以,,,为顶点的四边形为矩形,请直接写出所有符合条件的点的坐标,并写出其中一种求解点坐标的过程.
答案解析部分
1.【答案】B
【知识点】待定系数法求一次函数解析式;列一次函数关系式
2.【答案】B
【知识点】一次函数的概念
3.【答案】D
【知识点】一次函数图象、性质与系数的关系
4.【答案】B
【知识点】一次函数图象、性质与系数的关系
5.【答案】D
【知识点】待定系数法求一次函数解析式
6.【答案】A
【知识点】一次函数图象、性质与系数的关系
7.【答案】A
【知识点】一次函数图象、性质与系数的关系
8.【答案】C
【知识点】一次函数图象、性质与系数的关系
9.【答案】C
【知识点】通过函数图象获取信息
10.【答案】D
【知识点】通过函数图象获取信息
11.【答案】减小
【知识点】正比例函数的图象和性质
12.【答案】-40
【知识点】函数值
13.【答案】三;减小
【知识点】一次函数的性质
14.【答案】
【知识点】用关系式表示变量间的关系
15.【答案】3
【知识点】分式方程的解及检验;解分式方程;一次函数图象、性质与系数的关系
16.【答案】①②④
【知识点】一次函数的实际应用
17.【答案】解:当 时, ,当 时,
解得:
【知识点】待定系数法求一次函数解析式
18.【答案】(1)13.5
(2)y=0.5x+12
(3)14.75cm
(4)16kg
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
19.【答案】(1);(2)元;(3)小聪最多可以购买杨梅,寄送方式为8件,1件.
【知识点】一元一次方程的其他应用;一元一次不等式的应用;用关系式表示变量间的关系
20.【答案】(1)20;0.06;0.3
(2)爸爸比小明早60min到达营地
【知识点】通过函数图象获取信息
21.【答案】(1)
(2)或
【知识点】点的坐标;一次函数的概念;待定系数法求一次函数解析式
22.【答案】解:(1)提出概念所用的时间和对概念接受能力y两个变量;
(2)当时间是5分钟时,学生的接受能力是53.5;
(3)当提出概念13分钟时,学生的接受能力最强59.9;
(4)当2≤x≤13时,y值逐渐增大,学生的接受能力逐步增强;
当13≤x≤20时,y值逐渐减小,学生的接受能力逐步降低.
【知识点】常量、变量;函数的表示方法
23.【答案】(1)直线的解析式为;
(2)点的坐标为;
(3)点的坐标为或或或.
【知识点】待定系数法求一次函数解析式;矩形的判定与性质;旋转的性质
21世纪教育网(www.21cnjy.com)
10 / 10
【专项培优】湘教版数学八年级下册第四章一次函数
一、单选题
1.(2023八下·泸县月考)对于一次函数 y = kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,
x -1 0 1 3
y 7 5 2 -1
其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A.-1 B.2 C.5 D.7
2.(2023八上·海州期中)下列函数:①;②;③;④,其中一次函数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2024九上·南皮月考)关于的一元二次方程的根的情况,叙述正确的是( )
A.方程没有实数根
B.方程有两个实数根
C.若直线不经过第三象限,则方程有两个不相等的实数根
D.若直线不经过第一象限,则方程有两个不相等的实数根
4.(2019八上·永登期末)一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( )
A.-2 B.2 C.1 D.-2或2
5.(2023六下·岱岳期末)在某一阶段,某商品的销售量y与销售价x之间存在如表关系:
销售价x/元 90 100 110 120 130 140
销售量y/件 90 80 70 60 50 40
以下结论错误的是( )
A.当时, B.当时,
C.当时, D.当时,
6.(2021八下·台州期中)直线y=kx+b和y=bx+k在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
7.(2020七上·福山期末)直线和在同一平面直角坐标系内的大致图象为( ).
A. B.
C. D.
8.(2023八下·湖南期末)若,函数的图像不经过第( )象限
A.一 B.二 C.三 D.四
9.(2023八上·济南期中)在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7N时,拉力F=2.2N;
③拉力F与重力G成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N.
A.①② B.②④ C.①④ D.③④
10.(2023九上·东平月考)学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要
B.水温下降过程中,y与x的函数关系式是
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.水温不低于30℃的时间为
二、填空题
11.(2021九下·浦东期中)已知正比例函数,那么y的值随x的值增大而 (填“增大或“减小”)
12.(2021八下·武进月考)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y= x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
13.(2017八下·宣城期末)直线y= 不经过第 象限,y随x的增大而 .
14.(2024七下·榕城期末)王大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为米,要围成的菜园是如图所示的长方形,设边的长为米,边的长为米,则与的关系式是 .
15.(2024八上·沅江开学考)已知关于的分式方程有整数解,且一次函数图象经过第一、二、三象限,则整数的值为 .
16.(2020八上·包河期末)如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是 .
①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
三、计算题
17.(2019七下·二道期中)在 中,当 时, ,当 时, ,求 和 的值.
18.(2023七下·泗县期末)探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3kg时,弹簧的长度是 ;
(2)在弹性限度内如果所挂物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20cm,那么该弹簧最多能挂质量为多少的物体?
19.(2024九下·凤凰模拟)根据以下素材.探索完成任务.
杨梅季将至,梅企与某快递公司合作寄送杨梅.
素材1 某快递公司规定: 1.从当地寄送杨梅到A市按重量收费:当杨梅重量不超过10千克时,需要寄送费32元;当重量超过10千克时,超过部分另收m元/千克. 2.寄送杨梅重量均为整数千克.
素材2 电子存单1托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:7千克 件数:1 总费用:32元
电子存单2托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:12千克 件数:1 总费用:44元
电子存单3托寄物:杨梅 包装服务 产品类型:某快递公司 计量重量:15千克 件数:1 总费用:62元
问题解决
任务1 分析变量关系 根据以上信息,请确定m的值,并求出杨梅重量超过10千克时寄送费用y(元)关于杨梅重量x(千克)之间的函数关系式.
任务2 计算最省费用 若杨梅重量达到25千克,请求出最省的寄送费用.
任务3 探索最大重量 小聪想在当地梅企购买一批价格为50元/千克的杨梅并全部寄送给在A市的朋友们,若小聪能用来支配的钱有5000元,他最多可以购买多少千克的杨梅?并写出一种寄送方式.
四、解答题
20.(2022七下·成都期末)周末,小明和爸爸从家出发去青龙湖公园露营,早上9:00小明徒步先行出发,爸爸带上露营物资骑自行车后出发,到达露营地扎营.行进过程中爸爸和小明行驶速度均保持不变,两人离家的距离与时间如图所示.请根据图象回答问题:
(1)爸爸比小明晚出发_____min:小明徒步的速度是_____km/min﹔爸爸骑自行车的速度是____km/min;
(2)爸爸比小明早多久到达营地
21.(2024八下·福州期中)已知与成正比例,且时.
(1)求y与x之间的函数关系式;
(2)由(1)得到的函数图象上有一点P到x轴的距离为4,求点P坐标.
22.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤30)
提出概念所 用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59.0 59.8 59.9 59.8 58.3 55.0
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用时间是5分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(4)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
23.(2024八下·济南期末)如图1,在平面直角坐标系中,一次函数的图象分别交轴,轴于,两点,将绕点顺时针旋转得(点与点对应,点与点对应).
(1)直接写出直线的解析式;
(2)点为线段上一点,过点作轴交直线于点,作轴交直线于点,当时,求点的坐标;
(3)如图,若点为线段的中点,点为直线上一点,点为坐标系内一点.且以,,,为顶点的四边形为矩形,请直接写出所有符合条件的点的坐标,并写出其中一种求解点坐标的过程.
答案解析部分
1.【答案】B
【知识点】待定系数法求一次函数解析式;列一次函数关系式
2.【答案】B
【知识点】一次函数的概念
3.【答案】D
【知识点】一次函数图象、性质与系数的关系
4.【答案】B
【知识点】一次函数图象、性质与系数的关系
5.【答案】D
【知识点】待定系数法求一次函数解析式
6.【答案】A
【知识点】一次函数图象、性质与系数的关系
7.【答案】A
【知识点】一次函数图象、性质与系数的关系
8.【答案】C
【知识点】一次函数图象、性质与系数的关系
9.【答案】C
【知识点】通过函数图象获取信息
10.【答案】D
【知识点】通过函数图象获取信息
11.【答案】减小
【知识点】正比例函数的图象和性质
12.【答案】-40
【知识点】函数值
13.【答案】三;减小
【知识点】一次函数的性质
14.【答案】
【知识点】用关系式表示变量间的关系
15.【答案】3
【知识点】分式方程的解及检验;解分式方程;一次函数图象、性质与系数的关系
16.【答案】①②④
【知识点】一次函数的实际应用
17.【答案】解:当 时, ,当 时,
解得:
【知识点】待定系数法求一次函数解析式
18.【答案】(1)13.5
(2)y=0.5x+12
(3)14.75cm
(4)16kg
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
19.【答案】(1);(2)元;(3)小聪最多可以购买杨梅,寄送方式为8件,1件.
【知识点】一元一次方程的其他应用;一元一次不等式的应用;用关系式表示变量间的关系
20.【答案】(1)20;0.06;0.3
(2)爸爸比小明早60min到达营地
【知识点】通过函数图象获取信息
21.【答案】(1)
(2)或
【知识点】点的坐标;一次函数的概念;待定系数法求一次函数解析式
22.【答案】解:(1)提出概念所用的时间和对概念接受能力y两个变量;
(2)当时间是5分钟时,学生的接受能力是53.5;
(3)当提出概念13分钟时,学生的接受能力最强59.9;
(4)当2≤x≤13时,y值逐渐增大,学生的接受能力逐步增强;
当13≤x≤20时,y值逐渐减小,学生的接受能力逐步降低.
【知识点】常量、变量;函数的表示方法
23.【答案】(1)直线的解析式为;
(2)点的坐标为;
(3)点的坐标为或或或.
【知识点】待定系数法求一次函数解析式;矩形的判定与性质;旋转的性质
21世纪教育网(www.21cnjy.com)
10 / 10
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
