湖北省黄石十四中2024-2025学年第二学期期中八年级数学试卷(无答案)
文档属性
| 名称 | 湖北省黄石十四中2024-2025学年第二学期期中八年级数学试卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 210.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 00:00:00 | ||
图片预览


文档简介
2024—2025学年八年级下学期4月期中质量检测
数学试卷
(本试卷共6页,满分120分,考试用时120分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题卡上指定的位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效,作图一律用2B铅笔或黑色签字笔。
4. 考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共10题,每题3分,共30分.在每题给出的四个选项中,只有一项符合题目要求)
1. 下列二次根式是最简二次根式的是
D.
2. 下列运算,正确的是
3. 下列四组线段a、b、c,能组成直角三角形的是
A. a=8,b=15,c=17
C. a=2,b=3,c=4 D. a=4,b=5,c=6
4. 工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形,其中的道理是
A.两点之间,线段最短
B.两点确定一条直线
C.对角线相等的四边形是矩形
D.对角线相等的平行四边形是矩形
5. 下列命题的逆命题成立的是
A.如果两个实数相等,那么它们的绝对值相等
B.全等三角形的对应角相等
C.如果直角三角形的两条直角边长分别为a、b,斜边为c,那么
D.对顶角相等
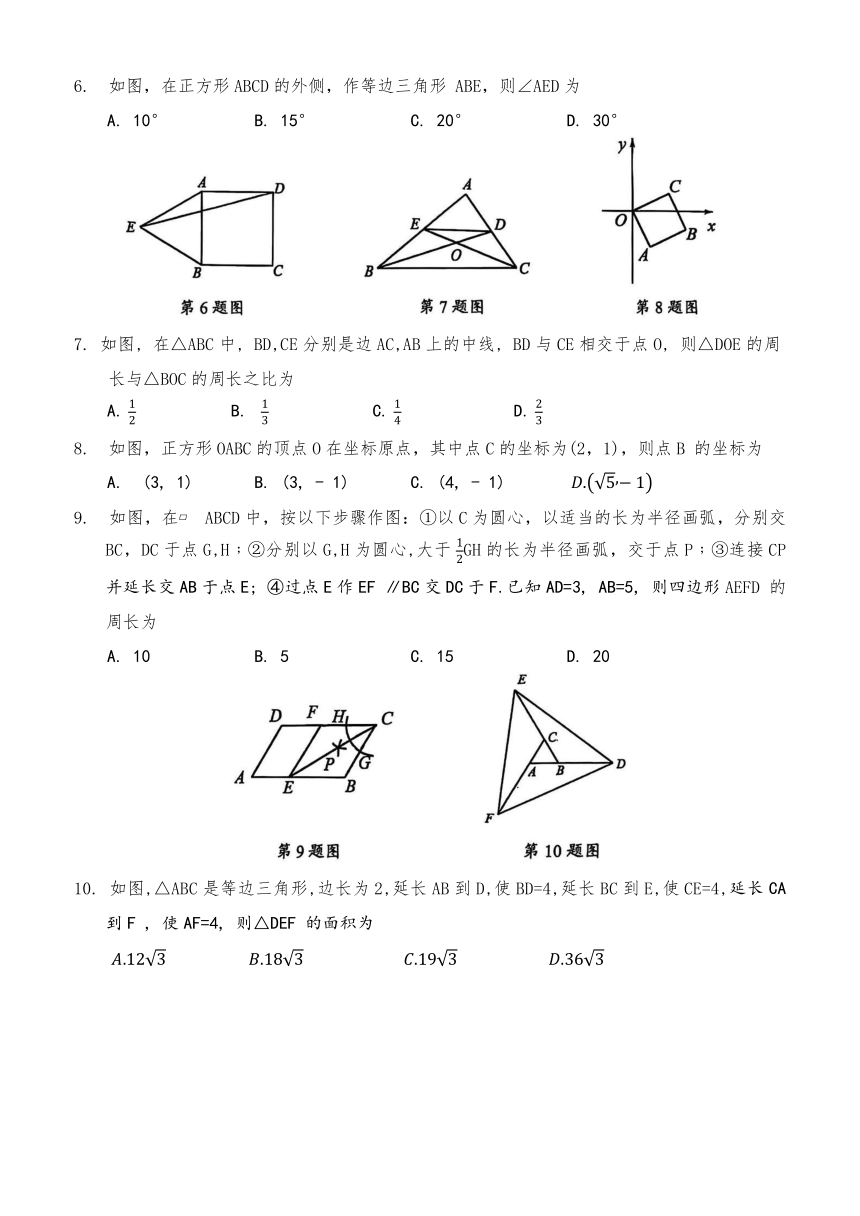
6. 如图,在正方形ABCD的外侧,作等边三角形 ABE,则∠AED为
A. 10° B. 15° C. 20° D. 30°
7. 如图, 在△ABC中, BD,CE分别是边AC,AB上的中线, BD与CE相交于点O, 则△DOE的周长与△BOC的周长之比为
A. B. C. D.
8. 如图,正方形OABC的顶点O在坐标原点,其中点C的坐标为(2,1),则点B 的坐标为
A. (3, 1) B. (3, - 1) C. (4, - 1)
9. 如图,在 ABCD中,按以下步骤作图:①以C为圆心,以适当的长为半径画弧,分别交BC,DC于点G,H﹔②分别以G,H为圆心,大于 GH的长为半径画弧,交于点P﹔③连接CP并延长交AB于点E; ④过点E作EF ∥BC交DC于F.已知AD=3, AB=5, 则四边形AEFD 的周长为
A. 10 B. 5 C. 15 D. 20
10. 如图,△ABC是等边三角形,边长为2,延长AB到D,使BD=4,延长BC到E,使CE=4,延长CA到F , 使AF=4, 则△DEF 的面积为
二、填空题(共5题,每题3分,共15分)
11. 式子 有意义,则x的取值范围是 .
12.新定义 例如 则
13. 如图, 菱形ABCD的对角线AC=24, BD=10, 则菱形的面积为 .
14. 如图, 在Rt△ABC中, ∠ACB=90°, 点D,E分别是AC,BC的中点, 则DE= .
15. 如图, 把矩形ABCD沿EF对折, 使点B与点D重合, 折痕EF 交BD于G, P为DG上一个动点, 若FC=2, DC=4, 则PF+PC的最小值为 .
三、解答题(共9题,共75分,解答应写出文字说明、证明过程或演算步骤)
16. (6分)
计算:
17. (6分)
如图,在四边形ABCD中,. 交BD于点E, 交BD于点F,且BE=DF .求证: 四边形ABCD是平行四边形.
18. (6分)
学校科技兴趣小组利用无人机测量学校旗杆的高度.无人机在距离地面60米的C处测得旗杆底部B 的俯角为( (即 CE为水平线,测得旗杆顶部A的俯角为 (即 请通过以上数据求学校旗杆的高度(精确到0.1米,
19. (8分)
如图,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
是直角吗 请说明理由.
20. (8分)
如图,在 中, CE 平分. CF平分 的外角 ,过点A作 垂足为M, 垂足为N,连接MN交AC于点O.
(1) 求证:
(2)当线段AC和MN满足什么条件时,四边形AMCN为正方形.
楚天名初试题研究院*数学试卷 (共6 页)第4 页
21. (8分)
如图,正方形ABCD的边长为10,E,F 分别是边DC, AB的中点,点G 是线段DE上一点,将 沿AG翻折,点D的对应点. 正好落在线段EF 上.
(1) 求 的度数;
(2) 求线段GE的长.
22. (10分)
如图1,正方形ABCD和正方形AEFG 的顶点A重合,正方形AEFG的对角线EG过点D,BD是正方形ABCD的对角线.
(1) 求证:
(2) 如图2, 点H是DG的中点, 连接AH , 求AH 的值.
23. (11分)
【问题提出】如图1, E是菱形 ABCD边BC上一点, 是等腰三角形, ∠AEF=∠ABC=α(α≥60°), 探究∠DCF 与α的数量关系.
(1) 【问题探究】先将问题特殊化,如图2, 当α=90°时,直接写出. 的大小:∠DCF= ;
(2)再探究一般情形,如图1,求∠DCF 与α的数量关系;
(3)【问题拓展】将图1特殊化,如图3,当α=60°时, 求菱形ABCD的面积.
24. (12分)
如图1,在四边形ABCD中, AD∥BC, ∠B=90°, AB=12cm, AD=30cm, BC=35cm.点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P,Q运动的时间为 ts.
(1) 当t= s时, PQ∥CD;
(2) 如图1, 从运动开始, 当t为何值时, QP=QD;
(3)从运动开始,当t为何值时,四边形ABQP 为矩形;
(4)从运动开始,当t为何值时,△QDC为直角三角形.
数学试卷
(本试卷共6页,满分120分,考试用时120分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题卡上指定的位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效,作图一律用2B铅笔或黑色签字笔。
4. 考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共10题,每题3分,共30分.在每题给出的四个选项中,只有一项符合题目要求)
1. 下列二次根式是最简二次根式的是
D.
2. 下列运算,正确的是
3. 下列四组线段a、b、c,能组成直角三角形的是
A. a=8,b=15,c=17
C. a=2,b=3,c=4 D. a=4,b=5,c=6
4. 工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形,其中的道理是
A.两点之间,线段最短
B.两点确定一条直线
C.对角线相等的四边形是矩形
D.对角线相等的平行四边形是矩形
5. 下列命题的逆命题成立的是
A.如果两个实数相等,那么它们的绝对值相等
B.全等三角形的对应角相等
C.如果直角三角形的两条直角边长分别为a、b,斜边为c,那么
D.对顶角相等
6. 如图,在正方形ABCD的外侧,作等边三角形 ABE,则∠AED为
A. 10° B. 15° C. 20° D. 30°
7. 如图, 在△ABC中, BD,CE分别是边AC,AB上的中线, BD与CE相交于点O, 则△DOE的周长与△BOC的周长之比为
A. B. C. D.
8. 如图,正方形OABC的顶点O在坐标原点,其中点C的坐标为(2,1),则点B 的坐标为
A. (3, 1) B. (3, - 1) C. (4, - 1)
9. 如图,在 ABCD中,按以下步骤作图:①以C为圆心,以适当的长为半径画弧,分别交BC,DC于点G,H﹔②分别以G,H为圆心,大于 GH的长为半径画弧,交于点P﹔③连接CP并延长交AB于点E; ④过点E作EF ∥BC交DC于F.已知AD=3, AB=5, 则四边形AEFD 的周长为
A. 10 B. 5 C. 15 D. 20
10. 如图,△ABC是等边三角形,边长为2,延长AB到D,使BD=4,延长BC到E,使CE=4,延长CA到F , 使AF=4, 则△DEF 的面积为
二、填空题(共5题,每题3分,共15分)
11. 式子 有意义,则x的取值范围是 .
12.新定义 例如 则
13. 如图, 菱形ABCD的对角线AC=24, BD=10, 则菱形的面积为 .
14. 如图, 在Rt△ABC中, ∠ACB=90°, 点D,E分别是AC,BC的中点, 则DE= .
15. 如图, 把矩形ABCD沿EF对折, 使点B与点D重合, 折痕EF 交BD于G, P为DG上一个动点, 若FC=2, DC=4, 则PF+PC的最小值为 .
三、解答题(共9题,共75分,解答应写出文字说明、证明过程或演算步骤)
16. (6分)
计算:
17. (6分)
如图,在四边形ABCD中,. 交BD于点E, 交BD于点F,且BE=DF .求证: 四边形ABCD是平行四边形.
18. (6分)
学校科技兴趣小组利用无人机测量学校旗杆的高度.无人机在距离地面60米的C处测得旗杆底部B 的俯角为( (即 CE为水平线,测得旗杆顶部A的俯角为 (即 请通过以上数据求学校旗杆的高度(精确到0.1米,
19. (8分)
如图,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
是直角吗 请说明理由.
20. (8分)
如图,在 中, CE 平分. CF平分 的外角 ,过点A作 垂足为M, 垂足为N,连接MN交AC于点O.
(1) 求证:
(2)当线段AC和MN满足什么条件时,四边形AMCN为正方形.
楚天名初试题研究院*数学试卷 (共6 页)第4 页
21. (8分)
如图,正方形ABCD的边长为10,E,F 分别是边DC, AB的中点,点G 是线段DE上一点,将 沿AG翻折,点D的对应点. 正好落在线段EF 上.
(1) 求 的度数;
(2) 求线段GE的长.
22. (10分)
如图1,正方形ABCD和正方形AEFG 的顶点A重合,正方形AEFG的对角线EG过点D,BD是正方形ABCD的对角线.
(1) 求证:
(2) 如图2, 点H是DG的中点, 连接AH , 求AH 的值.
23. (11分)
【问题提出】如图1, E是菱形 ABCD边BC上一点, 是等腰三角形, ∠AEF=∠ABC=α(α≥60°), 探究∠DCF 与α的数量关系.
(1) 【问题探究】先将问题特殊化,如图2, 当α=90°时,直接写出. 的大小:∠DCF= ;
(2)再探究一般情形,如图1,求∠DCF 与α的数量关系;
(3)【问题拓展】将图1特殊化,如图3,当α=60°时, 求菱形ABCD的面积.
24. (12分)
如图1,在四边形ABCD中, AD∥BC, ∠B=90°, AB=12cm, AD=30cm, BC=35cm.点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P,Q运动的时间为 ts.
(1) 当t= s时, PQ∥CD;
(2) 如图1, 从运动开始, 当t为何值时, QP=QD;
(3)从运动开始,当t为何值时,四边形ABQP 为矩形;
(4)从运动开始,当t为何值时,△QDC为直角三角形.
同课章节目录
