北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 13:23:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
2.下列式子中,不能用平方差公式运算的是( )
A.(﹣x﹣y)(﹣x+y) B.(﹣x+y)(x﹣y)
C.(y+x)(x﹣y) D.(y﹣x)(x+y)
3.小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.3,下列说法正确的是( )
A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中3次
D.小星定点投篮3次,一定投中1次
4.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
5.计算的结果是( )
A. B. C. D.
6.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
7.二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),若从二十四个节气中选一个节气,则抽到的节气在冬季的概率为( )
A. B. C. D.
8.若(x+1)(x2﹣5ax+a)的乘积中不含x2项,则常数a的值为( )
A.5 B. C. D.﹣5
9.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.若知道下列条件,仍不能求S1﹣S2值的是( )
A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差
10.如图,FG∥HK,一块三角板的顶点A在直线HK上,边BC、AC分别交直线FG于D、E两点.∠BAC=60°,∠B=90°,∠C=30°.点I在∠EDC的平分线上,连接AI,且∠CAI:∠KAI=1:3,若∠I=32°,则∠FDB的度数为( )
A.32° B.38°
C.42° D.44°
二、填空题(6小题,每题3分,共18分)
11.在一个不透明的袋子里装有若干个红球和12个黄球,这些球除颜色不同外,其余均相同.每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定于0.2.估计袋中红球的个数是 .
12.小刚将二维码打印在面积为10的正方形纸片上,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,多次试验后获得如下数据,由此可以估计此二维码中黑色阴影部分的面积为 .(结果保留整数)
重复试验次数 30 50 100 300 800
点落在阴影部分次数 19 32 59 183 483
“点落在阴影部分”的频率(结果保留两位小数) 0.67 0.64 0.59 0.61 0.60
13.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
15.若2a=3,2b=6,2c=12,则a、b、c的关系:①c=a+2;②c﹣b=1;③a+c=2b;④a+b=c+1,其中正确的是 .
16.小明将(2022x+2023)2展开后得到;小亮将(2023x﹣2022)2展开后得到,若两人计算过程无误,则c1﹣c2的值为 .
第II卷
北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2)(14x2y3﹣7xy2)÷(7xy).
18.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
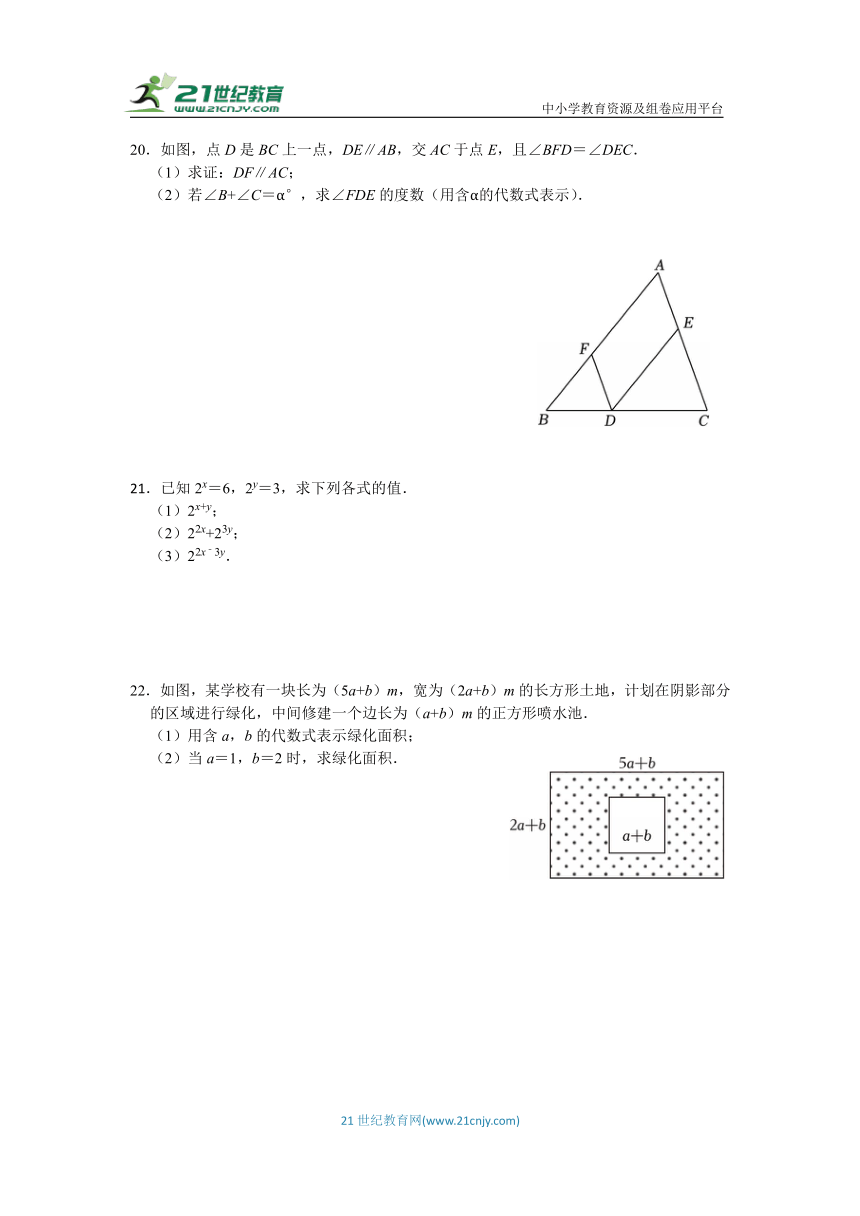
20.如图,点D是BC上一点,DE∥AB,交AC于点E,且∠BFD=∠DEC.
(1)求证:DF∥AC;
(2)若∠B+∠C=α°,求∠FDE的度数(用含α的代数式表示).
21.已知2x=6,2y=3,求下列各式的值.
(1)2x+y;
(2)22x+23y;
(3)22x﹣3y.
22.如图,某学校有一块长为(5a+b)m,宽为(2a+b)m的长方形土地,计划在阴影部分的区域进行绿化,中间修建一个边长为(a+b)m的正方形喷水池.
(1)用含a,b的代数式表示绿化面积;
(2)当a=1,b=2时,求绿化面积.
23.规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ,(﹣2,﹣32)= ;
(2)若(4,5)=a,(4,6)=b,(4,30)=c,试探究a,b,c之间存在的数量关系;
(3)若(m,8)+(m,3)=(m,t),求t的值.
24.如图,直线AB∥CD,EF∥GH,∠AEF的角平分线交CD于点P.
(1)∠EPF与∠PEF相等吗?请说明理由.
(2)若∠FHG=3∠EPF,求∠EFD的度数.
(3)点Q为射线GH上一点,连结EQ,FQ.若∠QFH=∠FQH,且∠PEQ﹣∠EQF=50°,求∠EQF的度数.
25.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
参考答案
选择题
1—10:ABBCB BABDB
二、填空题
11.【解答】解:设袋中红球有x个,
根据题意,得:0.2,
解得:x=3,
经检验,x=3是方程的解,
∴估计袋中红球的个数是3个.
故答案为:3.
12.【解答】解:∵经过大量重复实验,发现点落在黑色阴影的频率稳定在0.6左右,
∴估计点落在黑色阴影的概率为0.6,
∴黑色阴影的面积为10×0.6=6.
故答案为:6.
13.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
14.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
15.【解答】解:已知2a=3,2b=6,2c=12,
∵3×4=3×22=12,
∴2a×22=2c,
∴2a+2=2c,
∴c=a+2,则①正确;
∵12÷6=2,
∴2c÷2b=2,
∴2c﹣b=2,
∴c﹣b=1,则②正确;
∵3×12=36=62,
∴2a 2c=(2b)2,
∴2a+c=22b,
∴a+c=2b,则③正确;
∵2a+b=2a 2b=3×6=18,2c+1=2c×2=12×2=24,
∴2a+b≠2c+1,
∴a+b≠c+1,则④错误;
综上,正确的是①②③,
故答案为:①②③.
16.【解答】解:∵(2022x+2023)2展开后得到,
∴c1=20232,
∵(2023x﹣2022)2展开后得到,
∴c2=20222,
∴c1﹣c2=20232﹣20222
=(2023+2022)(2023﹣2022)
=4045×1
=4045,
故答案为:4045.
三、解答题
17.【解答】解:(1)原式=1+1+4
=6;
(2)原式=14x2y3÷7xy﹣7xy2÷7xy
=2xy2﹣y.
18.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵DE∥AB,
∴∠A=∠DEC.
∵∠DEC+∠AFD=180°,
∴∠A+∠AFD=180°.
∴DF∥AC.
(2)解:∵DE∥AB,
∴∠EDC=∠B.
∵DF∥AC,
∴∠FDB=∠C.
∵∠FDE+∠FDB+∠EDC=180°,∠B+∠C=α°,
∴∠FDE=180°﹣(∠FDB+∠EDC)
=180°﹣(∠B+∠C).
=180°﹣α°.
21.【解答】解:(1)∵2x=6,2y=3,
∴2x+y=2x 2y=6×3=18;
(2)∵2x=6,2y=3,
∴22x+23y=(2x)2+(2y)3=62+33=36+27=63;
(3)∵2x=6,2y=3,
∴;
22.解:(1)S草坪=S长方形一S正方形=(5a+b)(2a+b)﹣(a+b)2=10a2+5ab+2ab+b2﹣a2﹣2ab﹣b2=9a2+5ab,
∴绿化面积为(9a2+5ab)平方米;
(2)当a=1,b=2时,
S草坪=9a2+5ab=9+10=19(平方米),
答:绿化面积为19平方米.
23.【解答】解:(1)∵53=125,(﹣2)5=﹣32,
∴(5,125)=3,(﹣2,﹣32)=5,
故答案为:3,5;
(2)a+b=c,理由如下:
∵(4,5)=a,(4,6)=b,(4,30)=c,
∴4a=5,4b=6,4c=30,
∵5×6=30,
∴4a×4b=4c,即4a+b=4c,
∴a+b=c;
(3)设(m,8)=x,(m,3)=y,(m,t)=z,则mx=8,my=3,mz=t,
由(m,8)+(m,3)=(m,t)可得x+y=z,
∴t=mz=mx+y=mx×my=8×3=24.,
24.【解答】解:(1)∠EPF与∠PEF相等,理由如下:
∵EP是∠AEF的平分线,
∴∠PEA=∠PEF,
∵AB∥CD,
∴∠PEA=∠EPF,
∴∠EPF=∠PEF;
(2)设∠EPF=α,
∴∠FHG=3∠EPF=3α,
由(1)可知:∠EPF=∠PEF=∠PEA=α,
∴∠AEF=2α,
∵AB∥CD,
∴∠EFD=∠AEF=2α,
∵EF∥GH,
∴∠EFH+∠FHG=180°,
即2α+3α=180°,
解得:α=36°,
∴∠EFD=2α=72°;
(3)设∠EQF=β,
∵∠PEQ﹣∠EQF=50°,
∴∠PEQ=50°+β,
∵点Q为射线GH上一点,
∴有以下两种情况:
①当点Q在线段GH上时,如图1所示:
∵EF∥GH,
∴∠1=∠FQH,
∵∠QFH=∠FQH,
∴∠1=∠QFH,
∴∠1=∠EFD,
∵EP是∠AEF的平分线,
∴∠2=∠AEF,
∵AB∥CD,
∴∠AEF=∠EFD,
∴∠1=∠2,
∴PE∥FQ,
∴∠PEQ+∠EQF=180°,
即50°+β+β=180°,
解得:β=65°,
即∠EQF=β=65°;
②当点Q在线段GH的延长线上时,
过点Q作QR∥CD交EF的延长线于R,如图2所示:
∵EF∥GH,
∴∠1=∠FQH,∠3=∠QFH,
∵∠QFH=∠FQH,
∴∠1=∠QFH=∠3,
∴∠RFH=2∠1=2∠3,
∵∠RFH=∠PFE,
∴∠PFE=2∠3,
∵EP是∠AEF的平分线,
∴∠AEF=2∠2,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2∠3+2∠2=180°,
∴∠3+∠2=90°,
∵AB∥CD,QR∥CD,
∴AB∥QR,
∴∠AEQ+∠EQR=180°,
即∠2+50°+β+∠3+β=180°,
解得:β=20°,
∴∠EQF=β=20°,
综上所述:∠EQF的度数为65°或20°.
25.【解答】解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=[(x+y)2﹣(x2+y2)]
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得[(4﹣m)﹣(5﹣m)]2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=[(4﹣m)﹣(5﹣m)]2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
2.下列式子中,不能用平方差公式运算的是( )
A.(﹣x﹣y)(﹣x+y) B.(﹣x+y)(x﹣y)
C.(y+x)(x﹣y) D.(y﹣x)(x+y)
3.小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.3,下列说法正确的是( )
A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中3次
D.小星定点投篮3次,一定投中1次
4.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
5.计算的结果是( )
A. B. C. D.
6.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
7.二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),若从二十四个节气中选一个节气,则抽到的节气在冬季的概率为( )
A. B. C. D.
8.若(x+1)(x2﹣5ax+a)的乘积中不含x2项,则常数a的值为( )
A.5 B. C. D.﹣5
9.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.若知道下列条件,仍不能求S1﹣S2值的是( )
A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差
10.如图,FG∥HK,一块三角板的顶点A在直线HK上,边BC、AC分别交直线FG于D、E两点.∠BAC=60°,∠B=90°,∠C=30°.点I在∠EDC的平分线上,连接AI,且∠CAI:∠KAI=1:3,若∠I=32°,则∠FDB的度数为( )
A.32° B.38°
C.42° D.44°
二、填空题(6小题,每题3分,共18分)
11.在一个不透明的袋子里装有若干个红球和12个黄球,这些球除颜色不同外,其余均相同.每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定于0.2.估计袋中红球的个数是 .
12.小刚将二维码打印在面积为10的正方形纸片上,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,多次试验后获得如下数据,由此可以估计此二维码中黑色阴影部分的面积为 .(结果保留整数)
重复试验次数 30 50 100 300 800
点落在阴影部分次数 19 32 59 183 483
“点落在阴影部分”的频率(结果保留两位小数) 0.67 0.64 0.59 0.61 0.60
13.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
15.若2a=3,2b=6,2c=12,则a、b、c的关系:①c=a+2;②c﹣b=1;③a+c=2b;④a+b=c+1,其中正确的是 .
16.小明将(2022x+2023)2展开后得到;小亮将(2023x﹣2022)2展开后得到,若两人计算过程无误,则c1﹣c2的值为 .
第II卷
北师大版2024—2025学年七年级下册数学期中考试模拟试卷(一)
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2)(14x2y3﹣7xy2)÷(7xy).
18.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.如图,点D是BC上一点,DE∥AB,交AC于点E,且∠BFD=∠DEC.
(1)求证:DF∥AC;
(2)若∠B+∠C=α°,求∠FDE的度数(用含α的代数式表示).
21.已知2x=6,2y=3,求下列各式的值.
(1)2x+y;
(2)22x+23y;
(3)22x﹣3y.
22.如图,某学校有一块长为(5a+b)m,宽为(2a+b)m的长方形土地,计划在阴影部分的区域进行绿化,中间修建一个边长为(a+b)m的正方形喷水池.
(1)用含a,b的代数式表示绿化面积;
(2)当a=1,b=2时,求绿化面积.
23.规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ,(﹣2,﹣32)= ;
(2)若(4,5)=a,(4,6)=b,(4,30)=c,试探究a,b,c之间存在的数量关系;
(3)若(m,8)+(m,3)=(m,t),求t的值.
24.如图,直线AB∥CD,EF∥GH,∠AEF的角平分线交CD于点P.
(1)∠EPF与∠PEF相等吗?请说明理由.
(2)若∠FHG=3∠EPF,求∠EFD的度数.
(3)点Q为射线GH上一点,连结EQ,FQ.若∠QFH=∠FQH,且∠PEQ﹣∠EQF=50°,求∠EQF的度数.
25.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
参考答案
选择题
1—10:ABBCB BABDB
二、填空题
11.【解答】解:设袋中红球有x个,
根据题意,得:0.2,
解得:x=3,
经检验,x=3是方程的解,
∴估计袋中红球的个数是3个.
故答案为:3.
12.【解答】解:∵经过大量重复实验,发现点落在黑色阴影的频率稳定在0.6左右,
∴估计点落在黑色阴影的概率为0.6,
∴黑色阴影的面积为10×0.6=6.
故答案为:6.
13.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
14.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
15.【解答】解:已知2a=3,2b=6,2c=12,
∵3×4=3×22=12,
∴2a×22=2c,
∴2a+2=2c,
∴c=a+2,则①正确;
∵12÷6=2,
∴2c÷2b=2,
∴2c﹣b=2,
∴c﹣b=1,则②正确;
∵3×12=36=62,
∴2a 2c=(2b)2,
∴2a+c=22b,
∴a+c=2b,则③正确;
∵2a+b=2a 2b=3×6=18,2c+1=2c×2=12×2=24,
∴2a+b≠2c+1,
∴a+b≠c+1,则④错误;
综上,正确的是①②③,
故答案为:①②③.
16.【解答】解:∵(2022x+2023)2展开后得到,
∴c1=20232,
∵(2023x﹣2022)2展开后得到,
∴c2=20222,
∴c1﹣c2=20232﹣20222
=(2023+2022)(2023﹣2022)
=4045×1
=4045,
故答案为:4045.
三、解答题
17.【解答】解:(1)原式=1+1+4
=6;
(2)原式=14x2y3÷7xy﹣7xy2÷7xy
=2xy2﹣y.
18.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵DE∥AB,
∴∠A=∠DEC.
∵∠DEC+∠AFD=180°,
∴∠A+∠AFD=180°.
∴DF∥AC.
(2)解:∵DE∥AB,
∴∠EDC=∠B.
∵DF∥AC,
∴∠FDB=∠C.
∵∠FDE+∠FDB+∠EDC=180°,∠B+∠C=α°,
∴∠FDE=180°﹣(∠FDB+∠EDC)
=180°﹣(∠B+∠C).
=180°﹣α°.
21.【解答】解:(1)∵2x=6,2y=3,
∴2x+y=2x 2y=6×3=18;
(2)∵2x=6,2y=3,
∴22x+23y=(2x)2+(2y)3=62+33=36+27=63;
(3)∵2x=6,2y=3,
∴;
22.解:(1)S草坪=S长方形一S正方形=(5a+b)(2a+b)﹣(a+b)2=10a2+5ab+2ab+b2﹣a2﹣2ab﹣b2=9a2+5ab,
∴绿化面积为(9a2+5ab)平方米;
(2)当a=1,b=2时,
S草坪=9a2+5ab=9+10=19(平方米),
答:绿化面积为19平方米.
23.【解答】解:(1)∵53=125,(﹣2)5=﹣32,
∴(5,125)=3,(﹣2,﹣32)=5,
故答案为:3,5;
(2)a+b=c,理由如下:
∵(4,5)=a,(4,6)=b,(4,30)=c,
∴4a=5,4b=6,4c=30,
∵5×6=30,
∴4a×4b=4c,即4a+b=4c,
∴a+b=c;
(3)设(m,8)=x,(m,3)=y,(m,t)=z,则mx=8,my=3,mz=t,
由(m,8)+(m,3)=(m,t)可得x+y=z,
∴t=mz=mx+y=mx×my=8×3=24.,
24.【解答】解:(1)∠EPF与∠PEF相等,理由如下:
∵EP是∠AEF的平分线,
∴∠PEA=∠PEF,
∵AB∥CD,
∴∠PEA=∠EPF,
∴∠EPF=∠PEF;
(2)设∠EPF=α,
∴∠FHG=3∠EPF=3α,
由(1)可知:∠EPF=∠PEF=∠PEA=α,
∴∠AEF=2α,
∵AB∥CD,
∴∠EFD=∠AEF=2α,
∵EF∥GH,
∴∠EFH+∠FHG=180°,
即2α+3α=180°,
解得:α=36°,
∴∠EFD=2α=72°;
(3)设∠EQF=β,
∵∠PEQ﹣∠EQF=50°,
∴∠PEQ=50°+β,
∵点Q为射线GH上一点,
∴有以下两种情况:
①当点Q在线段GH上时,如图1所示:
∵EF∥GH,
∴∠1=∠FQH,
∵∠QFH=∠FQH,
∴∠1=∠QFH,
∴∠1=∠EFD,
∵EP是∠AEF的平分线,
∴∠2=∠AEF,
∵AB∥CD,
∴∠AEF=∠EFD,
∴∠1=∠2,
∴PE∥FQ,
∴∠PEQ+∠EQF=180°,
即50°+β+β=180°,
解得:β=65°,
即∠EQF=β=65°;
②当点Q在线段GH的延长线上时,
过点Q作QR∥CD交EF的延长线于R,如图2所示:
∵EF∥GH,
∴∠1=∠FQH,∠3=∠QFH,
∵∠QFH=∠FQH,
∴∠1=∠QFH=∠3,
∴∠RFH=2∠1=2∠3,
∵∠RFH=∠PFE,
∴∠PFE=2∠3,
∵EP是∠AEF的平分线,
∴∠AEF=2∠2,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2∠3+2∠2=180°,
∴∠3+∠2=90°,
∵AB∥CD,QR∥CD,
∴AB∥QR,
∴∠AEQ+∠EQR=180°,
即∠2+50°+β+∠3+β=180°,
解得:β=20°,
∴∠EQF=β=20°,
综上所述:∠EQF的度数为65°或20°.
25.【解答】解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=[(x+y)2﹣(x2+y2)]
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得[(4﹣m)﹣(5﹣m)]2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=[(4﹣m)﹣(5﹣m)]2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
21世纪教育网(www.21cnjy.com)
同课章节目录
