浙教版2024—2025学年七年级下学期数学期中考试模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期中考试模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 426.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 00:00:00 | ||
图片预览



文档简介
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第三章整式的乘除
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.计算的结果等于( )
A.﹣5 B.5 C. D.
4.若(x﹣n)(x﹣2)=x2+5x+m,则常数m,n的值分别为( )
A.m=﹣14,n=7 B.m=14,n=﹣7
C.m=14,n=7 D.m=﹣14,n=﹣7
5.我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
6.方程组的解x,y的值互为相反数,则a的值是( )
A.12 B.﹣3.6 C.8 D.2.5
7.若a,b是正整数,且满足2a+2a+2a+2a=2b 2b 2b 2b,则a与b的关系正确的是( )
A.a+2=4b B.a=b C.a+2=b4 D.4a=b4
8.已知关于x,y的二元一次方程组的解为,则关于x,y的二元一次方程组的解为( )
A. B. C. D.
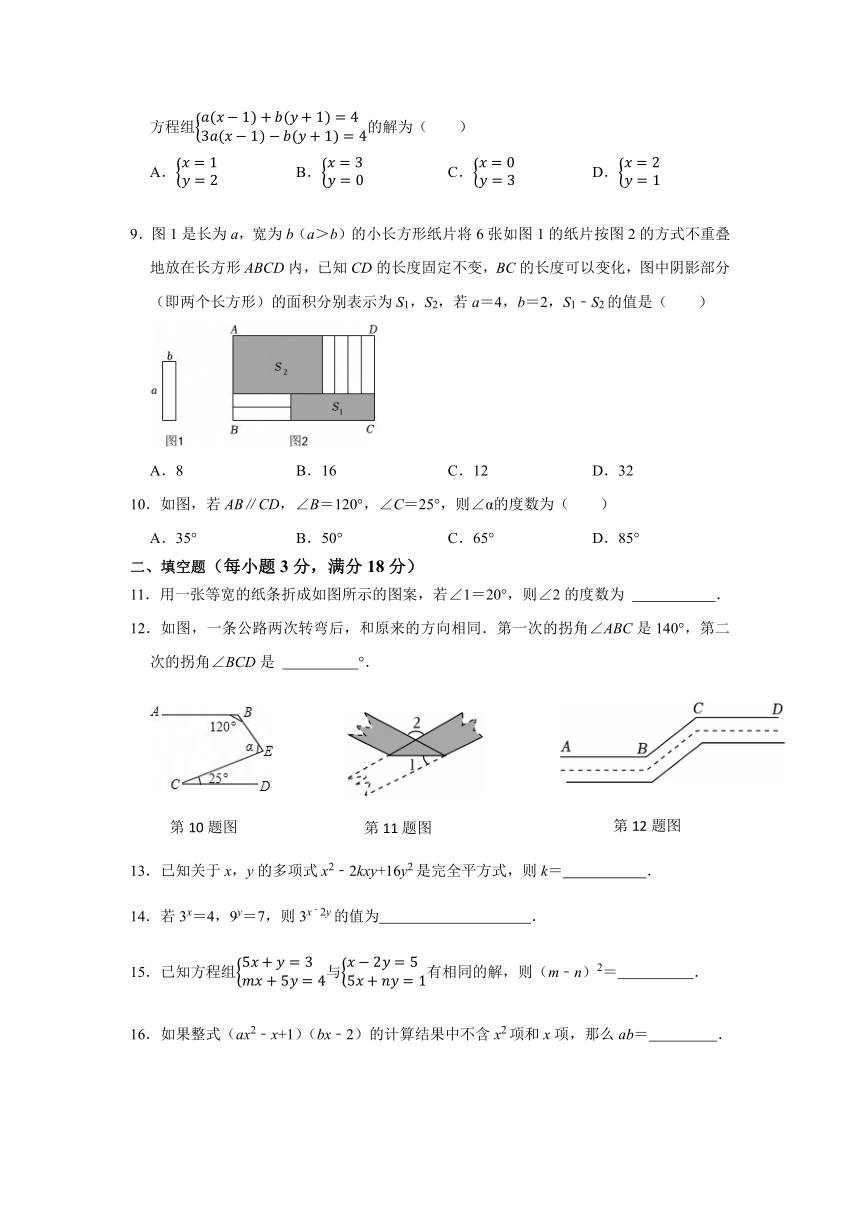
9.图1是长为a,宽为b(a>b)的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形ABCD内,已知CD的长度固定不变,BC的长度可以变化,图中阴影部分(即两个长方形)的面积分别表示为S1,S2,若a=4,b=2,S1﹣S2的值是( )
A.8 B.16 C.12 D.32
10.如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )
A.35° B.50° C.65° D.85°
二、填空题(每小题3分,满分18分)
11.用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
12.如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC是140°,第二次的拐角∠BCD是 °.
13.已知关于x,y的多项式x2﹣2kxy+16y2是完全平方式,则k= .
14.若3x=4,9y=7,则3x﹣2y的值为 .
15.已知方程组与有相同的解,则(m﹣n)2= .
16.如果整式(ax2﹣x+1)(bx﹣2)的计算结果中不含x2项和x项,那么ab= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
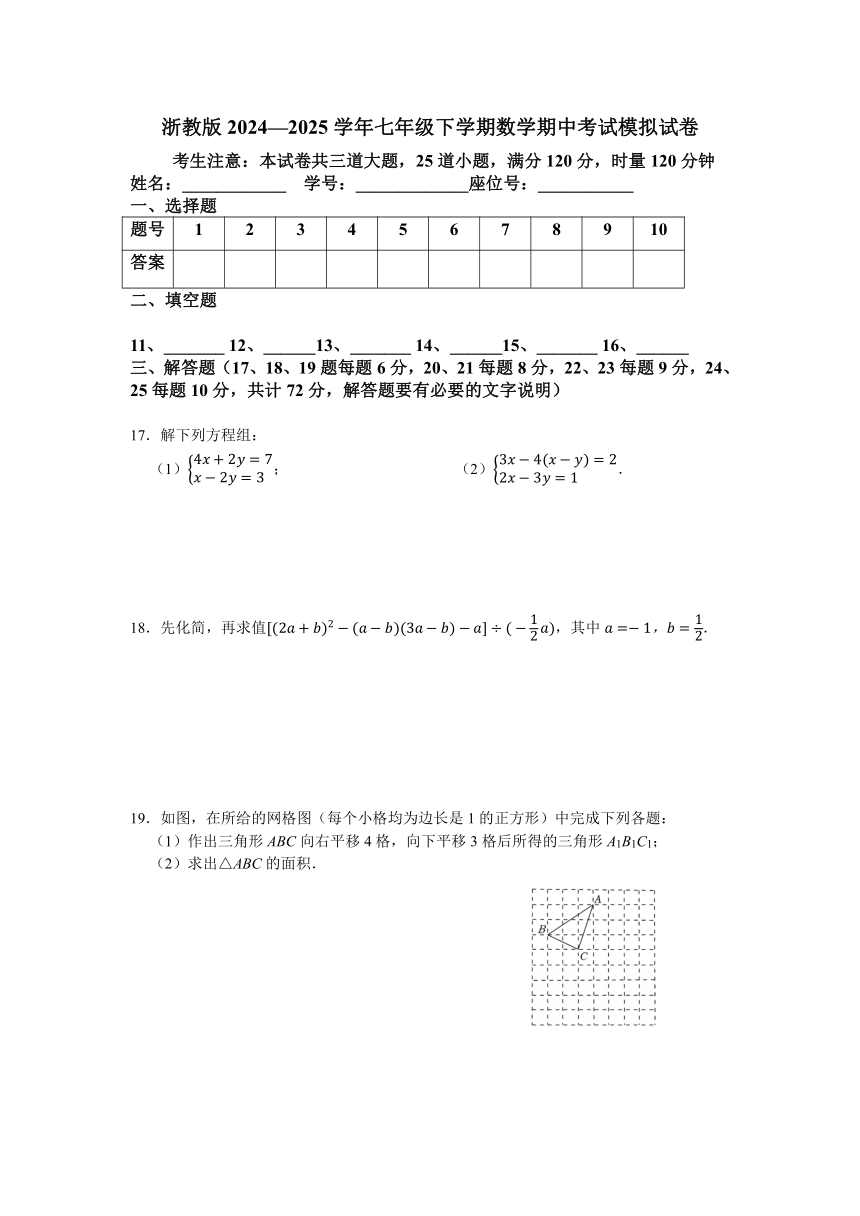
17.解下列方程组:
(1); (2).
18.先化简,再求值,其中.
19.如图,在所给的网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)作出三角形ABC向右平移4格,向下平移3格后所得的三角形A1B1C1;
(2)求出△ABC的面积.
20.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
21.某中学开设ADD的校本课程,购买了A,B两种型号的机器人模型,已知A型机器人模型单价比B型机器人模型单价多300元,购买3台A型机器人模型的费用比购买4台B型机器人模型的奇用多400元.
(1)请问A型,B型机器人模型的单价分别是多少元?
(2)现在学校要求买A、B两种机器人模型,刚好用完一万现金,有几种方案呢?
22.在解方程组时,由于粗心,甲看错了方程组中的a,得到的解为:乙看错了方程组中的b,得到的解为.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
23.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
24.定义:关于x,y的二元一次方程ax+by=c(其中a≠b≠c)中的常数项c与未知数系数a,b之一互换,得到的方程叫“交换系数方程”,例如:ax+by=c 的交换系数方程为cx+by=a或ax+cy=b.
(1)方程 3x+2y=4 与它的“交换系数方程”组成的方程组的解为 ;
(2)已知关于x,y的二元一次方程ax+by=c的系数满足a+b+c=0,且ax+by=c与它的“交换系数方程”组成的方程组的解恰好是关于x,y的二元一次方程mx+ny=p的一个解,求代数式(m+n)m﹣p(n+p)+2023的值;
(3)已知整数m,n,t满足条件t<n<8m,并且(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,求m的值.
25.【教材原题】观察图①,用等式表示图中图形的面积的运算为(a+b)2=a2+2ab+b2.
【类比探究】观察图②,用等式表示图中阴影部分图形的面积和的运算为 .
【应用】(1)根据图②所得的公式,若a+b=15,ab=4,则a2+b2= .
(2)若x满足(5﹣x)(x﹣1)=2,求(5﹣x)2+(x﹣1)2的值.
【拓展】如图③,某学校有一块梯形空地ABCD,AC⊥BD于点E,AE=DE,BE=CE.该校计划在△AED和△BEC区域内种花,在△CDE和△ABE的区域内种草.经测量种花区域的面积和为109平方米,米,求种草区域的面积和.
参考答案
一、选择题
1—5:DDBDA
6—10:BADBD
二、填空题
11.【解答】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
12.【解答】解:∵道路是平行的,
∴∠ABC=∠BCD=140°(两直线平行,内错角相等).
故答案为:140.
13.【解答】解:∵x2﹣2kxy+16y2=x2﹣kxy+(4y)2,
∴﹣2kxy=±2x×4y,
解得k=±4.
故答案为:4和﹣4.
14.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
15.【解答】解:原式=2x÷22y=2x÷4y.
故答案为:.
16.【解答】解:∵多项式(ax2﹣x+1)(bx﹣2)=abx3+(﹣2a﹣b)x2+(b+2)x﹣2不含x2项和x项,
∴﹣2a﹣b=0且b+2=0,
解得a=1,b=﹣2,
∴ab=﹣2.
故答案为:﹣2.
三、解答题
17.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
18.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
19.【解答】解:(1)如图,A1B1C1即为所求;
(2)△ABC的面积=3×32×31×21×3=3.5.
20.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
21.【解答】解:(1)设A型机器人模型的单价是x元,B型机器人模型的单价是y元,
根据题意得:,
解得:,
答:A型机器人模型的单价是800元,B型机器人模型的单价是500元;
(2)设学校购买m台A型机器人模型,n台B型机器人模型,
根据题意得:800m+500n=10000,
整理得:n=20m,
∵m、n均为正整数,
∴或,
∴有2种方案.
22.【解答】解:(1)由题意得,
解得;
(2)把a、b的值代入得,,
①×2得,﹣2x+10y=30③,
②+③得,2x=28,
解得x=14,
把x=14代入①得,﹣14+5y=15,
解得y,
所以,原方程组的正确解是.
23.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
24.【解答】解:(1)∵方程3x+2y=4的“交换系数方程”为4x+2y=3或3x+4y=2,
∴方程 3x+2y=4 与它的“交换系数方程”组成的方程组为①或②.
∴方程组①的解为,方程组②的解为.
故答案为:或.
(2)方程ax+by=c与它的“交换系数方程”组成的方程组为①或②.
∴方程组①的解为.当a+b+c=0时,方程组①的解为;
方程组②的解为.当a+b+c=0时,方程组②的解为 .
∴方程ax+by=c与它的“交换系数方程”组成的方程组解为.
将代入mx+ny=p,得﹣(m+n)=p.
∴(m+n)m﹣p(n+p)+2023=﹣pm﹣pn﹣p2+2023=﹣p(m+n)﹣p2+2023=(﹣p)2﹣p2+2023=2023.
(3)(1+n)x+2023y=2m+2的“交换系数方程”为(2m+2)x+2023y=1+n或(1+n)x+(2m+2)y=2023.
∵(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,
∴(10m﹣t)x+2023y=m+t各系数与(2m+2)x+2023y=1+n各系数对应相等,得①,
∴(10m﹣t)x+2023y=m+t各系数与(1+n)x+(2m+2)y=2023各系数对应相等,得②.
解方程组①得.
∵t<n<8m,
∴tt+2,解得6<t<22(t为整数).
∴8<t+2<24,
∴若m为整数,必须有t+2=16,此时m=2.
∴t=14.
当t=14时,n15.
∴m=2.
解方程组②得m(不是整数),
∴方程组②的解不符合题意,需舍去.
综上,m=2.
25.【解答】解:【类比探究】观察图②,用等式表示图中阴影部分图形的面积和的运算为a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(1)∵a+b=15,ab=4,a2+b2=(a+b)2﹣2ab,
∴a2+b2=152﹣2×4=217,
故答案为:217;
(2)设m=5﹣x,n=x﹣1,则m+n=4,mn=(5﹣x)(x﹣1)=2,
所以(5﹣x)2+(x﹣1)2
=m2+n2
=(m+n)2﹣2mn
=16﹣4
=12;
【拓展】设AE=DE=a,BE=CE=b,由题意得,a+b=AE+CE=AC=13,S△AED+S△BECa2b2=109,即a2+b2=218,
S种草区域=S△CDE+S△ABE
abab
=ab
=60,
即种草区域的面积和为60.
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第三章整式的乘除
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.计算的结果等于( )
A.﹣5 B.5 C. D.
4.若(x﹣n)(x﹣2)=x2+5x+m,则常数m,n的值分别为( )
A.m=﹣14,n=7 B.m=14,n=﹣7
C.m=14,n=7 D.m=﹣14,n=﹣7
5.我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
6.方程组的解x,y的值互为相反数,则a的值是( )
A.12 B.﹣3.6 C.8 D.2.5
7.若a,b是正整数,且满足2a+2a+2a+2a=2b 2b 2b 2b,则a与b的关系正确的是( )
A.a+2=4b B.a=b C.a+2=b4 D.4a=b4
8.已知关于x,y的二元一次方程组的解为,则关于x,y的二元一次方程组的解为( )
A. B. C. D.
9.图1是长为a,宽为b(a>b)的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形ABCD内,已知CD的长度固定不变,BC的长度可以变化,图中阴影部分(即两个长方形)的面积分别表示为S1,S2,若a=4,b=2,S1﹣S2的值是( )
A.8 B.16 C.12 D.32
10.如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )
A.35° B.50° C.65° D.85°
二、填空题(每小题3分,满分18分)
11.用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
12.如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC是140°,第二次的拐角∠BCD是 °.
13.已知关于x,y的多项式x2﹣2kxy+16y2是完全平方式,则k= .
14.若3x=4,9y=7,则3x﹣2y的值为 .
15.已知方程组与有相同的解,则(m﹣n)2= .
16.如果整式(ax2﹣x+1)(bx﹣2)的计算结果中不含x2项和x项,那么ab= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1); (2).
18.先化简,再求值,其中.
19.如图,在所给的网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)作出三角形ABC向右平移4格,向下平移3格后所得的三角形A1B1C1;
(2)求出△ABC的面积.
20.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
21.某中学开设ADD的校本课程,购买了A,B两种型号的机器人模型,已知A型机器人模型单价比B型机器人模型单价多300元,购买3台A型机器人模型的费用比购买4台B型机器人模型的奇用多400元.
(1)请问A型,B型机器人模型的单价分别是多少元?
(2)现在学校要求买A、B两种机器人模型,刚好用完一万现金,有几种方案呢?
22.在解方程组时,由于粗心,甲看错了方程组中的a,得到的解为:乙看错了方程组中的b,得到的解为.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
23.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
24.定义:关于x,y的二元一次方程ax+by=c(其中a≠b≠c)中的常数项c与未知数系数a,b之一互换,得到的方程叫“交换系数方程”,例如:ax+by=c 的交换系数方程为cx+by=a或ax+cy=b.
(1)方程 3x+2y=4 与它的“交换系数方程”组成的方程组的解为 ;
(2)已知关于x,y的二元一次方程ax+by=c的系数满足a+b+c=0,且ax+by=c与它的“交换系数方程”组成的方程组的解恰好是关于x,y的二元一次方程mx+ny=p的一个解,求代数式(m+n)m﹣p(n+p)+2023的值;
(3)已知整数m,n,t满足条件t<n<8m,并且(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,求m的值.
25.【教材原题】观察图①,用等式表示图中图形的面积的运算为(a+b)2=a2+2ab+b2.
【类比探究】观察图②,用等式表示图中阴影部分图形的面积和的运算为 .
【应用】(1)根据图②所得的公式,若a+b=15,ab=4,则a2+b2= .
(2)若x满足(5﹣x)(x﹣1)=2,求(5﹣x)2+(x﹣1)2的值.
【拓展】如图③,某学校有一块梯形空地ABCD,AC⊥BD于点E,AE=DE,BE=CE.该校计划在△AED和△BEC区域内种花,在△CDE和△ABE的区域内种草.经测量种花区域的面积和为109平方米,米,求种草区域的面积和.
参考答案
一、选择题
1—5:DDBDA
6—10:BADBD
二、填空题
11.【解答】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
12.【解答】解:∵道路是平行的,
∴∠ABC=∠BCD=140°(两直线平行,内错角相等).
故答案为:140.
13.【解答】解:∵x2﹣2kxy+16y2=x2﹣kxy+(4y)2,
∴﹣2kxy=±2x×4y,
解得k=±4.
故答案为:4和﹣4.
14.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
15.【解答】解:原式=2x÷22y=2x÷4y.
故答案为:.
16.【解答】解:∵多项式(ax2﹣x+1)(bx﹣2)=abx3+(﹣2a﹣b)x2+(b+2)x﹣2不含x2项和x项,
∴﹣2a﹣b=0且b+2=0,
解得a=1,b=﹣2,
∴ab=﹣2.
故答案为:﹣2.
三、解答题
17.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
18.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
19.【解答】解:(1)如图,A1B1C1即为所求;
(2)△ABC的面积=3×32×31×21×3=3.5.
20.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
21.【解答】解:(1)设A型机器人模型的单价是x元,B型机器人模型的单价是y元,
根据题意得:,
解得:,
答:A型机器人模型的单价是800元,B型机器人模型的单价是500元;
(2)设学校购买m台A型机器人模型,n台B型机器人模型,
根据题意得:800m+500n=10000,
整理得:n=20m,
∵m、n均为正整数,
∴或,
∴有2种方案.
22.【解答】解:(1)由题意得,
解得;
(2)把a、b的值代入得,,
①×2得,﹣2x+10y=30③,
②+③得,2x=28,
解得x=14,
把x=14代入①得,﹣14+5y=15,
解得y,
所以,原方程组的正确解是.
23.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
24.【解答】解:(1)∵方程3x+2y=4的“交换系数方程”为4x+2y=3或3x+4y=2,
∴方程 3x+2y=4 与它的“交换系数方程”组成的方程组为①或②.
∴方程组①的解为,方程组②的解为.
故答案为:或.
(2)方程ax+by=c与它的“交换系数方程”组成的方程组为①或②.
∴方程组①的解为.当a+b+c=0时,方程组①的解为;
方程组②的解为.当a+b+c=0时,方程组②的解为 .
∴方程ax+by=c与它的“交换系数方程”组成的方程组解为.
将代入mx+ny=p,得﹣(m+n)=p.
∴(m+n)m﹣p(n+p)+2023=﹣pm﹣pn﹣p2+2023=﹣p(m+n)﹣p2+2023=(﹣p)2﹣p2+2023=2023.
(3)(1+n)x+2023y=2m+2的“交换系数方程”为(2m+2)x+2023y=1+n或(1+n)x+(2m+2)y=2023.
∵(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,
∴(10m﹣t)x+2023y=m+t各系数与(2m+2)x+2023y=1+n各系数对应相等,得①,
∴(10m﹣t)x+2023y=m+t各系数与(1+n)x+(2m+2)y=2023各系数对应相等,得②.
解方程组①得.
∵t<n<8m,
∴tt+2,解得6<t<22(t为整数).
∴8<t+2<24,
∴若m为整数,必须有t+2=16,此时m=2.
∴t=14.
当t=14时,n15.
∴m=2.
解方程组②得m(不是整数),
∴方程组②的解不符合题意,需舍去.
综上,m=2.
25.【解答】解:【类比探究】观察图②,用等式表示图中阴影部分图形的面积和的运算为a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(1)∵a+b=15,ab=4,a2+b2=(a+b)2﹣2ab,
∴a2+b2=152﹣2×4=217,
故答案为:217;
(2)设m=5﹣x,n=x﹣1,则m+n=4,mn=(5﹣x)(x﹣1)=2,
所以(5﹣x)2+(x﹣1)2
=m2+n2
=(m+n)2﹣2mn
=16﹣4
=12;
【拓展】设AE=DE=a,BE=CE=b,由题意得,a+b=AE+CE=AC=13,S△AED+S△BECa2b2=109,即a2+b2=218,
S种草区域=S△CDE+S△ABE
abab
=ab
=60,
即种草区域的面积和为60.
同课章节目录
