2025年中考数学二轮复习专题4 一线三等角模型 课件(共20张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习专题4 一线三等角模型 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 430.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 00:00:00 | ||
图片预览



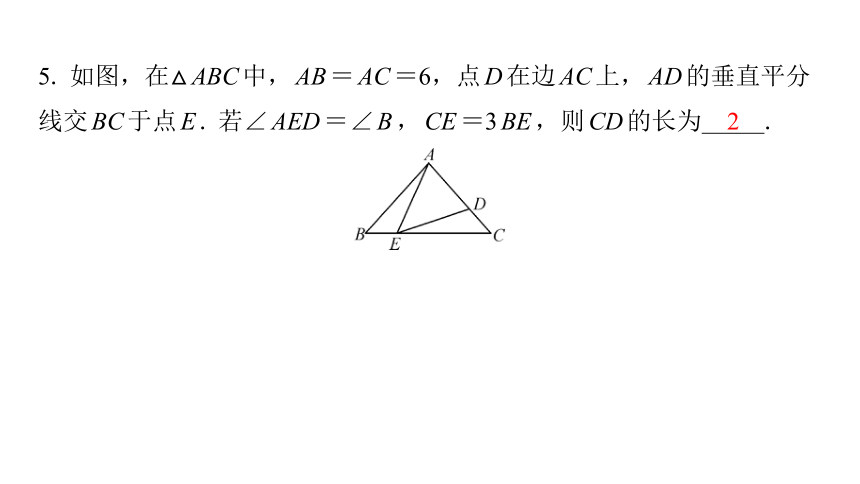
文档简介
(共20张PPT)
专题四 一线三等角模型
如图,三个相等角(∠1=∠2=∠3)的顶点在同一条直线上,可
利用三角形外角的性质定理得到两个三角形另一组角相等,进而可得
中间等角两侧的两个三角形全等或相似(△ACP≌△BPD或
△ACP∽△BPD).在具体运用该模型时,有边相等证全等,无边相等
证相似.
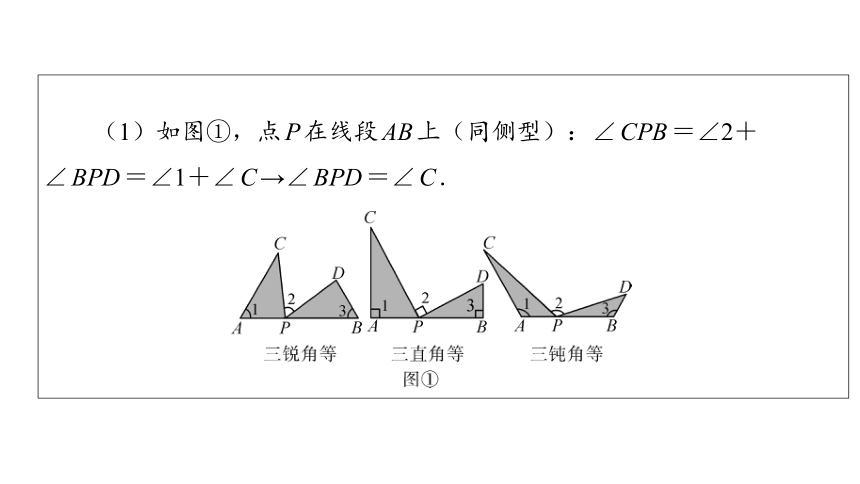
(1)如图①,点P在线段AB上(同侧型):∠CPB=∠2+
∠BPD=∠1+∠C→∠BPD=∠C.
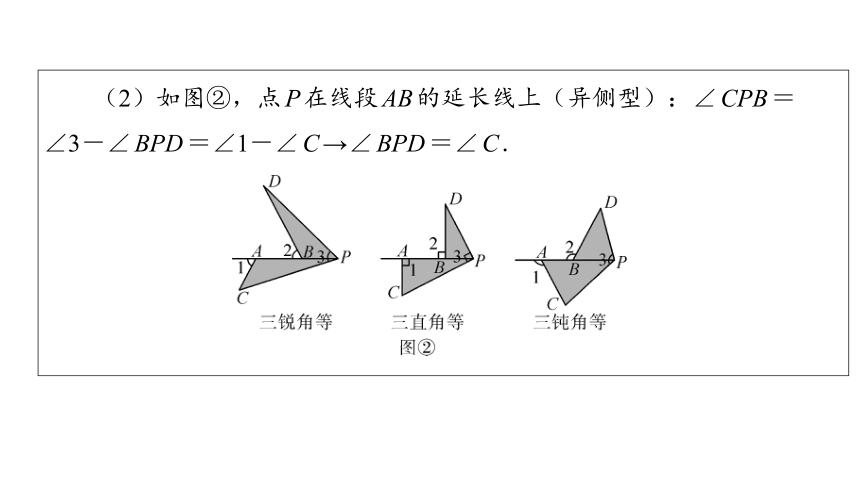
(2)如图②,点P在线段AB的延长线上(异侧型):∠CPB=
∠3-∠BPD=∠1-∠C→∠BPD=∠C.
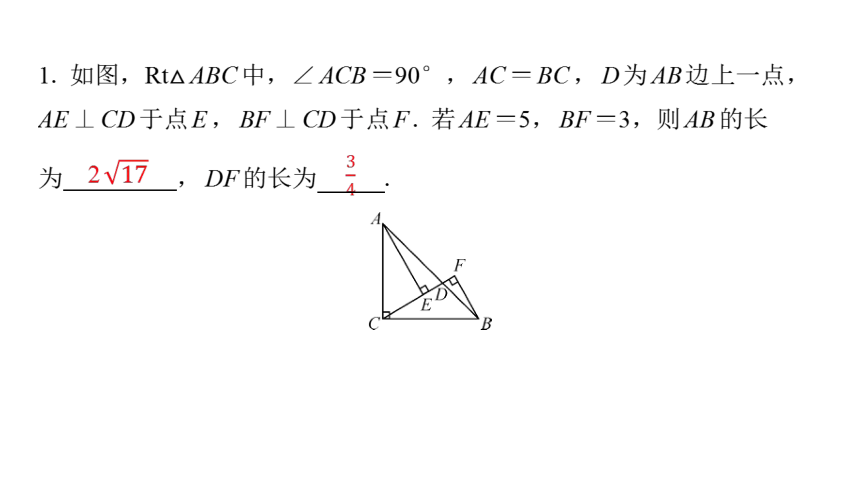
1. 如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,
AE⊥CD于点E,BF⊥CD于点F. 若AE=5,BF=3,则AB的长
为 2 ,DF的长为 .
2
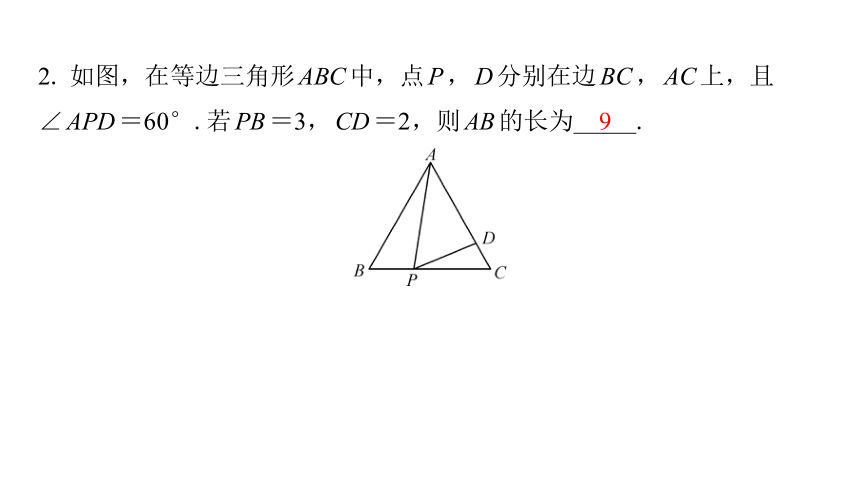
2. 如图,在等边三角形ABC中,点P,D分别在边BC,AC上,且
∠APD=60°.若PB=3,CD=2,则AB的长为 .
9
3. 如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,且CD
=2BD,点E,F在线段AD上,∠1=∠2=∠BAC. 若△ABC的面积
为15,则△ABE和△CDF的面积之和为 .
10
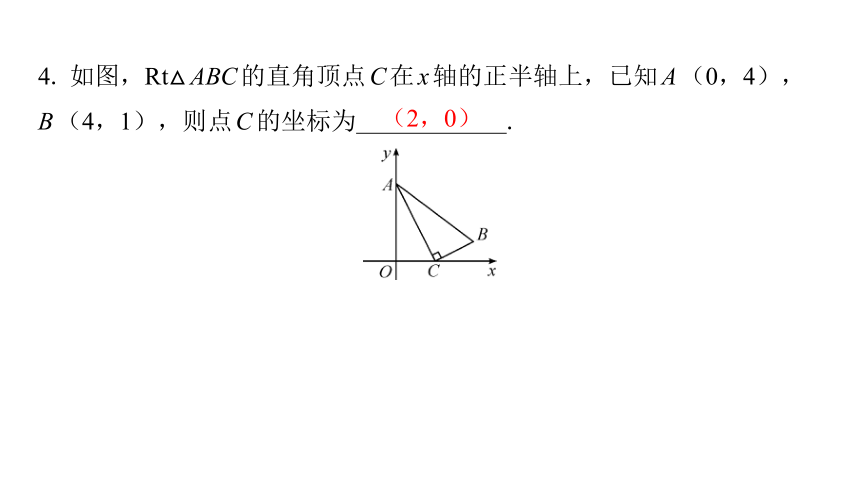
4. 如图,Rt△ABC的直角顶点C在x轴的正半轴上,已知A(0,4),
B(4,1),则点C的坐标为 .
(2,0)
5. 如图,在△ABC中,AB=AC=6,点D在边AC上,AD的垂直平分
线交BC于点E. 若∠AED=∠B,CE=3BE,则CD的长为 .
2
6. 如图,在平面直角坐标系中,A是双曲线y= (x>0)上任意一
点,连接OA,作OB⊥OA交双曲线y= (x<0)于点B. 若OA=
2OB,则 的值是 .
-4
7. 如图,D是等边三角形ABC边AB上的点,AD=2,BD=4,现将
△ABC折叠,使点C与点D重合,折痕为EF,且点E,F分别在边AC
和BC上,则 的值为 .
8. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作
EF⊥AE,交CD于点F,连接AF,求AF的最小值.
解:∵四边形ABCD为正方形,∴AB=BC=CD=AD=4,∠B=
∠C=90°,
∴∠BAE+∠AEB=90°.∵EF⊥AE,∴∠CEF+∠AEB=90°,
∴∠BAE=∠CEF. 又∠B=∠C=90°,∴△ABE∽△ECF,
∴ = .设BE=x,则 = ,
整理可得CF=- x2+x=- (x-2)2+1,∴当x=2时,CF取得
最大值为1,
当CF取得最大值1时,DF取得最小值为3.
∵AF= = =5,∴当DF=3时,AF取得最小值
为5.
9. 如图,在 ABCD中,AB=6,∠A=120°,点E,F分别在边
BC,AB上,DE=EF,∠DEF=120°.若CE=2,求 ABCD的周
长.
解:如图,在BC上截取BG=BF,连接FG.
∵AD∥BC,∠A=120°,∴∠B=60°,△BFG为等边三角形,
∴GF=BF=BG,∠BGF=60°,∴∠FGE=∠C=120°.
∵∠FEC=∠DEF+∠DEC=∠EFG+∠FGE,∠DEF=∠FGE=
120°,
∴∠DEC=∠EFG. 又∵DE=EF,∴△DEC≌△EFG(AAS),
∴GF=CE=2,EG=DC=AB=6,∴BC=BG+EG+CE=10.
∴ ABCD的周长为2(AB+BC)=
2×(6+10)=32.
10. 如图,已知点A(3,0),点B在y轴的正半轴上,将线段AB绕
点A顺时针旋转120°得到线段AC,若点C的坐标为(7,h),求h
的值.
解:如图,在x轴上取点D,E,使得∠ADB=∠AEC=120°,过点
C作CF⊥x轴于点F,
∴∠CEF=60°,EF= = h,CE= = h.
∵∠BAE=∠BAC+∠CAE=∠ADB+∠ABD,∠ADB=∠BAC=
120°,
∴∠CAE=∠ABD. 又∵AC=BA,∴△ACE≌△BAD(AAS),
∴AD=CE= h,∴OD=OA-AD=3- h,∴AE=BD=
2OD=6- h.
∵OA+AE+EF=OF=7,∴3+6- h+ h=7,解得h= .
谢谢观看
专题四 一线三等角模型
如图,三个相等角(∠1=∠2=∠3)的顶点在同一条直线上,可
利用三角形外角的性质定理得到两个三角形另一组角相等,进而可得
中间等角两侧的两个三角形全等或相似(△ACP≌△BPD或
△ACP∽△BPD).在具体运用该模型时,有边相等证全等,无边相等
证相似.
(1)如图①,点P在线段AB上(同侧型):∠CPB=∠2+
∠BPD=∠1+∠C→∠BPD=∠C.
(2)如图②,点P在线段AB的延长线上(异侧型):∠CPB=
∠3-∠BPD=∠1-∠C→∠BPD=∠C.
1. 如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,
AE⊥CD于点E,BF⊥CD于点F. 若AE=5,BF=3,则AB的长
为 2 ,DF的长为 .
2
2. 如图,在等边三角形ABC中,点P,D分别在边BC,AC上,且
∠APD=60°.若PB=3,CD=2,则AB的长为 .
9
3. 如图,在△ABC中,AB=AC,AB>BC,点D在边BC上,且CD
=2BD,点E,F在线段AD上,∠1=∠2=∠BAC. 若△ABC的面积
为15,则△ABE和△CDF的面积之和为 .
10
4. 如图,Rt△ABC的直角顶点C在x轴的正半轴上,已知A(0,4),
B(4,1),则点C的坐标为 .
(2,0)
5. 如图,在△ABC中,AB=AC=6,点D在边AC上,AD的垂直平分
线交BC于点E. 若∠AED=∠B,CE=3BE,则CD的长为 .
2
6. 如图,在平面直角坐标系中,A是双曲线y= (x>0)上任意一
点,连接OA,作OB⊥OA交双曲线y= (x<0)于点B. 若OA=
2OB,则 的值是 .
-4
7. 如图,D是等边三角形ABC边AB上的点,AD=2,BD=4,现将
△ABC折叠,使点C与点D重合,折痕为EF,且点E,F分别在边AC
和BC上,则 的值为 .
8. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作
EF⊥AE,交CD于点F,连接AF,求AF的最小值.
解:∵四边形ABCD为正方形,∴AB=BC=CD=AD=4,∠B=
∠C=90°,
∴∠BAE+∠AEB=90°.∵EF⊥AE,∴∠CEF+∠AEB=90°,
∴∠BAE=∠CEF. 又∠B=∠C=90°,∴△ABE∽△ECF,
∴ = .设BE=x,则 = ,
整理可得CF=- x2+x=- (x-2)2+1,∴当x=2时,CF取得
最大值为1,
当CF取得最大值1时,DF取得最小值为3.
∵AF= = =5,∴当DF=3时,AF取得最小值
为5.
9. 如图,在 ABCD中,AB=6,∠A=120°,点E,F分别在边
BC,AB上,DE=EF,∠DEF=120°.若CE=2,求 ABCD的周
长.
解:如图,在BC上截取BG=BF,连接FG.
∵AD∥BC,∠A=120°,∴∠B=60°,△BFG为等边三角形,
∴GF=BF=BG,∠BGF=60°,∴∠FGE=∠C=120°.
∵∠FEC=∠DEF+∠DEC=∠EFG+∠FGE,∠DEF=∠FGE=
120°,
∴∠DEC=∠EFG. 又∵DE=EF,∴△DEC≌△EFG(AAS),
∴GF=CE=2,EG=DC=AB=6,∴BC=BG+EG+CE=10.
∴ ABCD的周长为2(AB+BC)=
2×(6+10)=32.
10. 如图,已知点A(3,0),点B在y轴的正半轴上,将线段AB绕
点A顺时针旋转120°得到线段AC,若点C的坐标为(7,h),求h
的值.
解:如图,在x轴上取点D,E,使得∠ADB=∠AEC=120°,过点
C作CF⊥x轴于点F,
∴∠CEF=60°,EF= = h,CE= = h.
∵∠BAE=∠BAC+∠CAE=∠ADB+∠ABD,∠ADB=∠BAC=
120°,
∴∠CAE=∠ABD. 又∵AC=BA,∴△ACE≌△BAD(AAS),
∴AD=CE= h,∴OD=OA-AD=3- h,∴AE=BD=
2OD=6- h.
∵OA+AE+EF=OF=7,∴3+6- h+ h=7,解得h= .
谢谢观看
同课章节目录
