2025年中考数学二轮复习专题7 对角互补模型 课件(共16张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习专题7 对角互补模型 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 419.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 09:30:54 | ||
图片预览


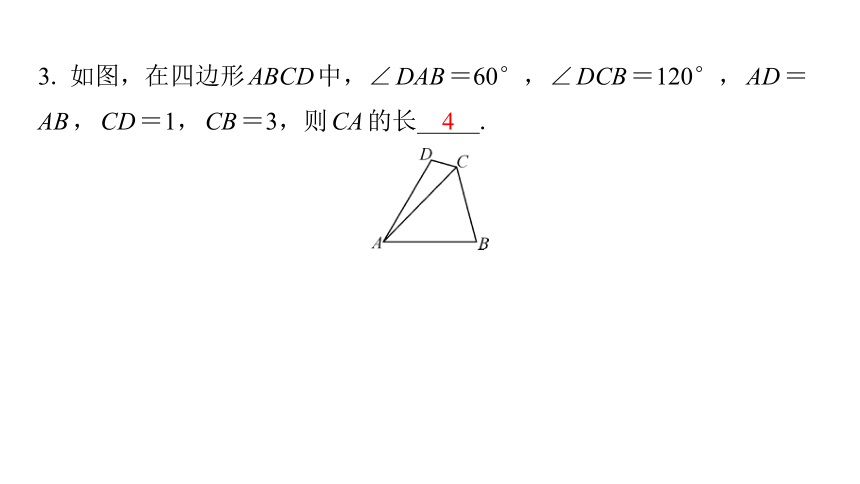
文档简介
(共16张PPT)
专题七 对角互补模型
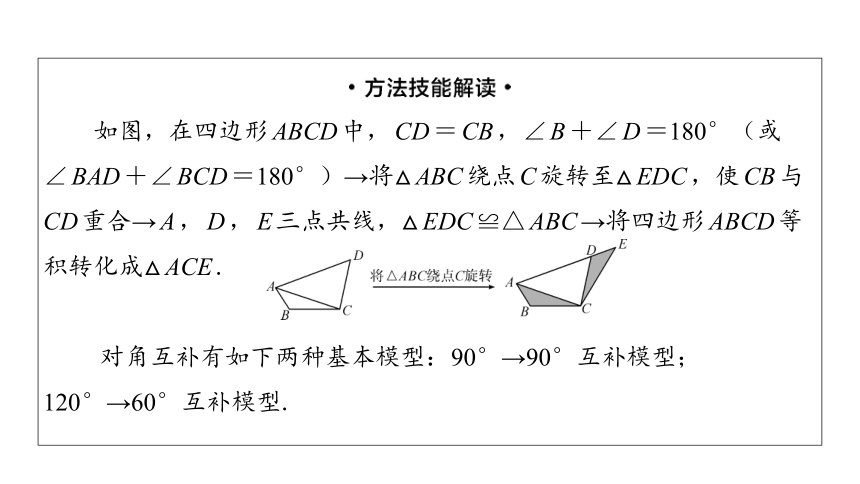
如图,在四边形ABCD中,CD=CB,∠B+∠D=180°(或
∠BAD+∠BCD=180°)→将△ABC绕点C旋转至△EDC,使CB与
CD重合→A,D,E三点共线,△EDC≌△ABC→将四边形ABCD等
积转化成△ACE.
对角互补有如下两种基本模型:90°→90°互补模型;120°→60°互补模型.
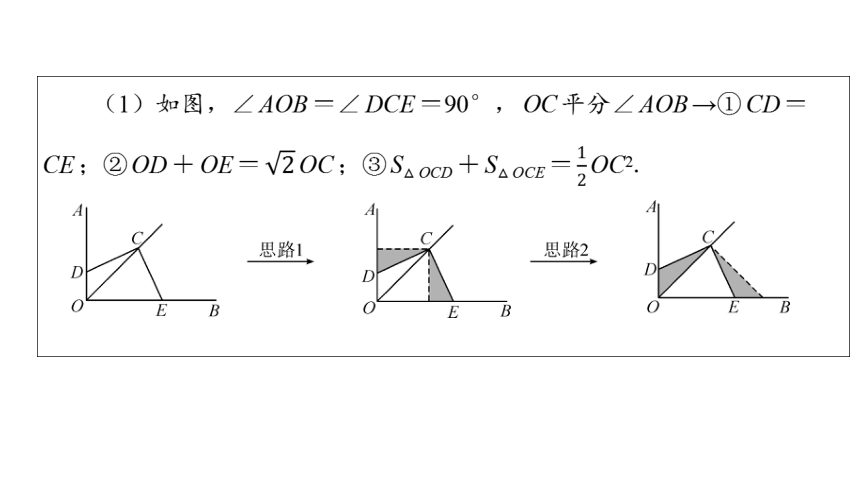
(1)如图,∠AOB=∠DCE=90°,OC平分∠AOB→①CD=
CE;②OD+OE= OC;③S△OCD+S△OCE= OC2.
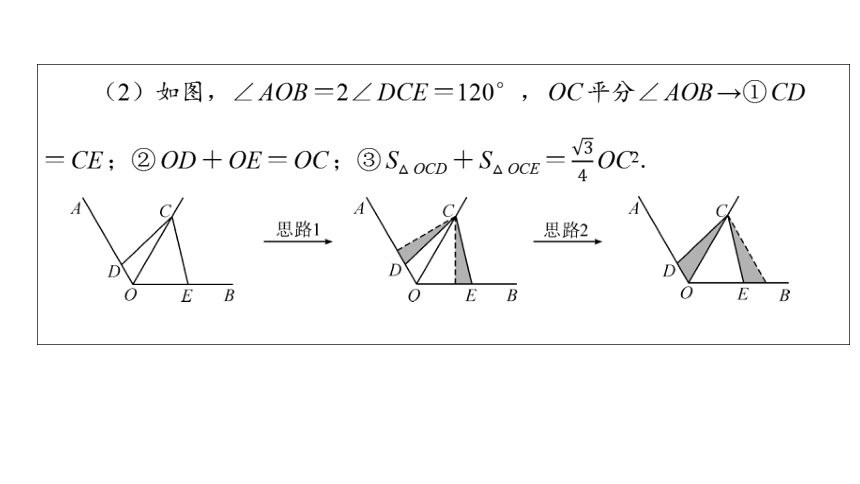
(2)如图,∠AOB=2∠DCE=120°,OC平分∠AOB→①CD
=CE;②OD+OE=OC;③S△OCD+S△OCE= OC2.
1. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连
接AC. 线段BC,CD,AC之间的数量关系是 .
BC+CD= AC
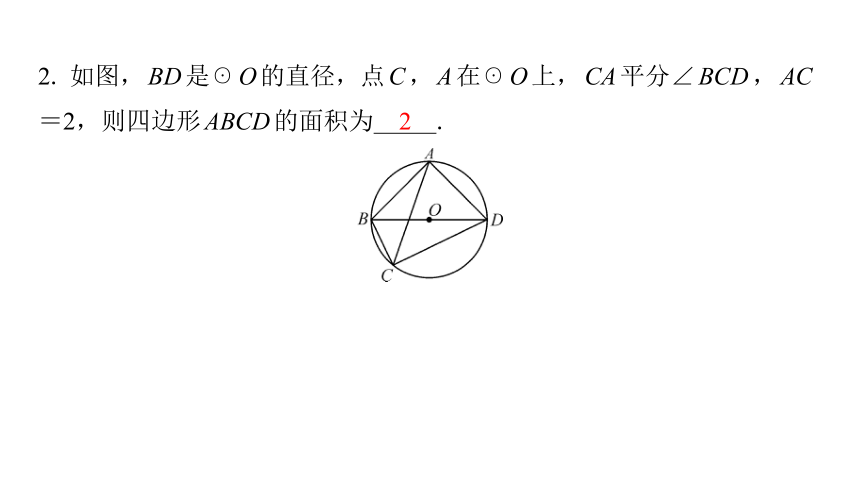
2. 如图,BD是☉O的直径,点C,A在☉O上,CA平分∠BCD,AC
=2,则四边形ABCD的面积为 .
2
3. 如图,在四边形ABCD中,∠DAB=60°,∠DCB=120°,AD=
AB,CD=1,CB=3,则CA的长 .
4
4. 如图,Rt△EPF的直角顶点P在矩形ABCD的对角线上,两直角边分
别与矩形的两邻边交于点M,N. 若AD= AB,则 的值为 .
5. 如图,正方形ABCD在平面直角坐标系中,对角线AC,BD相交于
点M. 若A(0,2),OM=3 ,求点C的坐标.
解:如图,过点M作MN⊥OM,交x轴于点N,连接CN.
∵ABCD为正方形,∴AM=BM,∠AMB=90°,
∴∠AMO+∠OMB=∠BMN+∠OMB=90°,∴∠AMO=∠BMN.
∵∠AOB=∠AMB=90°,∴∠MAO+∠MBO=180°.
∵∠MBN+∠MBO=180°,∴∠MAO=∠MBN,
∴△MAO≌△MBN(ASA),∴BN=AO=2,NM=OM=3 ,
∴ON= OM=3 × =6,∴OB=ON-BN=6-2=4.
∵AB=BC,∠BAO=∠CBN,AO=BN,∴△CBN≌△BAO
(SAS),
∴NC=OB=4,∠CNB=∠BOA=90°,∴CN⊥x轴,∴点C的坐
标为(6,4).
6. 如图,四边形ABCD内接于☉O,AC平分∠BCD. 若BC=m,
DC=n,∠BCD=2θ,求AC的长(用含m,n,θ的式子表示).
解:∵AC平分∠BCD,∴∠BCA=∠ACD,∴AB=AD.
如图,将△ACD绕点A顺时针旋转至△AFB,则△ABF≌△ADC,
∴BF=DC=n,∠ABF=∠ADC,∠F=∠ACD=θ,AF=AC.
又∵∠ABC+∠ADC=180°,∴∠ABC+∠ABF=180°,
∴F,B,C三点共线,∴CF=BF+BC=DC+BC=m+n.
如图,过点A作AE⊥BC于点E,则CE= CF= .
∵ cos ∠ACE= ,∴AC= = = .
7. 如图,在四边形ABCD中,对角线AC⊥AB,∠CAD=30°,
∠BCD=60°,求证:AB+2AD= AC.
证明:如图,作∠ECA=∠BCD=60°,交AB的延长线于点E,
∴∠ECB=∠ACD. 又∵AC⊥AB,∴∠E=30°=∠CAD,
∴△ECB∽△ACD,∴ = =2,即EB=2AD.
又∵tanE= ,∴tan30°= = ,
即 = ,整理可得AB+2AD= AC.
谢谢观看
专题七 对角互补模型
如图,在四边形ABCD中,CD=CB,∠B+∠D=180°(或
∠BAD+∠BCD=180°)→将△ABC绕点C旋转至△EDC,使CB与
CD重合→A,D,E三点共线,△EDC≌△ABC→将四边形ABCD等
积转化成△ACE.
对角互补有如下两种基本模型:90°→90°互补模型;120°→60°互补模型.
(1)如图,∠AOB=∠DCE=90°,OC平分∠AOB→①CD=
CE;②OD+OE= OC;③S△OCD+S△OCE= OC2.
(2)如图,∠AOB=2∠DCE=120°,OC平分∠AOB→①CD
=CE;②OD+OE=OC;③S△OCD+S△OCE= OC2.
1. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连
接AC. 线段BC,CD,AC之间的数量关系是 .
BC+CD= AC
2. 如图,BD是☉O的直径,点C,A在☉O上,CA平分∠BCD,AC
=2,则四边形ABCD的面积为 .
2
3. 如图,在四边形ABCD中,∠DAB=60°,∠DCB=120°,AD=
AB,CD=1,CB=3,则CA的长 .
4
4. 如图,Rt△EPF的直角顶点P在矩形ABCD的对角线上,两直角边分
别与矩形的两邻边交于点M,N. 若AD= AB,则 的值为 .
5. 如图,正方形ABCD在平面直角坐标系中,对角线AC,BD相交于
点M. 若A(0,2),OM=3 ,求点C的坐标.
解:如图,过点M作MN⊥OM,交x轴于点N,连接CN.
∵ABCD为正方形,∴AM=BM,∠AMB=90°,
∴∠AMO+∠OMB=∠BMN+∠OMB=90°,∴∠AMO=∠BMN.
∵∠AOB=∠AMB=90°,∴∠MAO+∠MBO=180°.
∵∠MBN+∠MBO=180°,∴∠MAO=∠MBN,
∴△MAO≌△MBN(ASA),∴BN=AO=2,NM=OM=3 ,
∴ON= OM=3 × =6,∴OB=ON-BN=6-2=4.
∵AB=BC,∠BAO=∠CBN,AO=BN,∴△CBN≌△BAO
(SAS),
∴NC=OB=4,∠CNB=∠BOA=90°,∴CN⊥x轴,∴点C的坐
标为(6,4).
6. 如图,四边形ABCD内接于☉O,AC平分∠BCD. 若BC=m,
DC=n,∠BCD=2θ,求AC的长(用含m,n,θ的式子表示).
解:∵AC平分∠BCD,∴∠BCA=∠ACD,∴AB=AD.
如图,将△ACD绕点A顺时针旋转至△AFB,则△ABF≌△ADC,
∴BF=DC=n,∠ABF=∠ADC,∠F=∠ACD=θ,AF=AC.
又∵∠ABC+∠ADC=180°,∴∠ABC+∠ABF=180°,
∴F,B,C三点共线,∴CF=BF+BC=DC+BC=m+n.
如图,过点A作AE⊥BC于点E,则CE= CF= .
∵ cos ∠ACE= ,∴AC= = = .
7. 如图,在四边形ABCD中,对角线AC⊥AB,∠CAD=30°,
∠BCD=60°,求证:AB+2AD= AC.
证明:如图,作∠ECA=∠BCD=60°,交AB的延长线于点E,
∴∠ECB=∠ACD. 又∵AC⊥AB,∴∠E=30°=∠CAD,
∴△ECB∽△ACD,∴ = =2,即EB=2AD.
又∵tanE= ,∴tan30°= = ,
即 = ,整理可得AB+2AD= AC.
谢谢观看
同课章节目录
