湘教版初中八年级下册数学 4.3.2 一次函数的图象与性质 课件(共28张PPT)
文档属性
| 名称 | 湘教版初中八年级下册数学 4.3.2 一次函数的图象与性质 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第四章 一次函数 4.3
一次函数的图象
4.3.2 一次函数的图象与性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.函数图象概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
2.一次函数的解析式:
y=kx+b(k≠0)
3.正比例函数的解析式:
y=kx(k≠0)
新课导入
4.作函数图象有几个步骤?
列表
描点
连线
5.正比例函数图象有什么特点?
正比例函数y=kx(k为常数,k≠0)的图象是经过点(0,0)和点(1,k)的一条直线,直线上的点与y=kx对应的x、y的值一一对应.
当k>0时,图象过一、三象限,y随x的增大而增大;
当k<0时,图象过二、四象限,y随x的增大而减小.
新课导入
思考
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?它们图象之间有什么关系?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
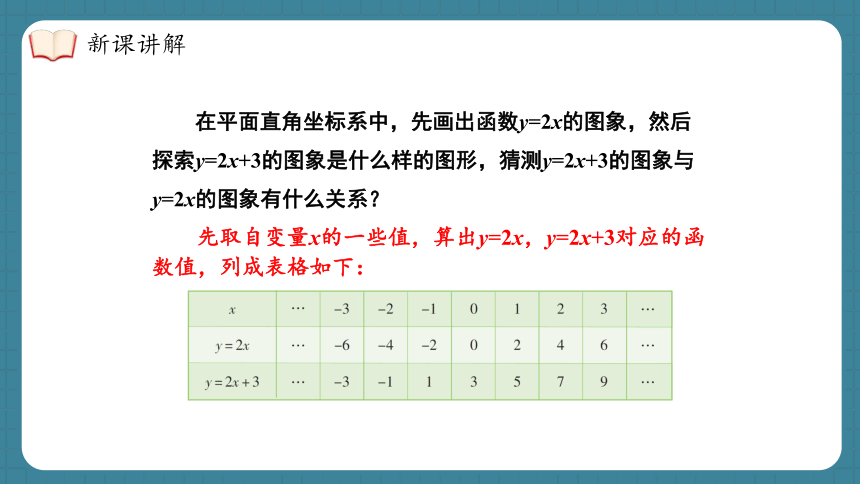
在平面直角坐标系中,先画出函数y=2x的图象,然后探索y=2x+3的图象是什么样的图形,猜测y=2x+3的图象与y=2x的图象有什么关系?
先取自变量x的一些值,算出y=2x,y=2x+3对应的函数值,列成表格如下:
新课讲解
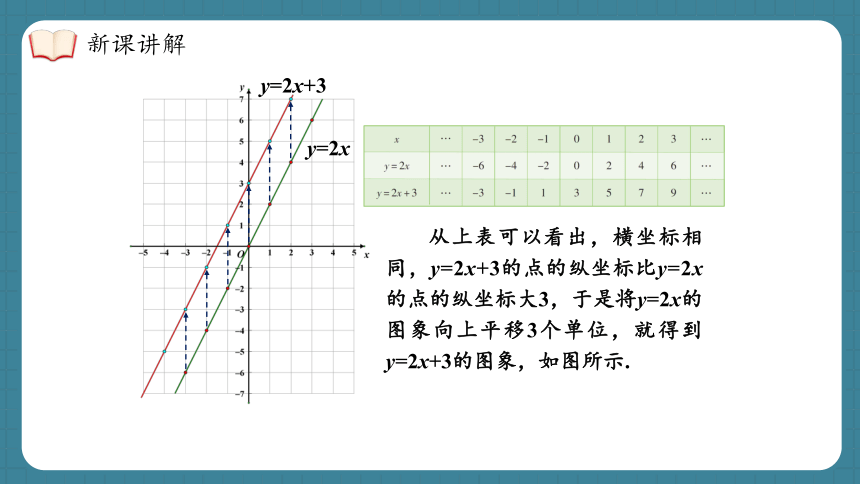
从上表可以看出,横坐标相同,y=2x+3的点的纵坐标比y=2x的点的纵坐标大3,于是将y=2x的图象向上平移3个单位,就得到y=2x+3的图象,如图所示.
y=2x
y=2x+3
新课讲解
观察两个函数图象发现:
相同点:都是一条直线;倾斜程度相同;y随x的增大而增大.
不同点:y=2x的图象过原点;y=2x+3的图象与y轴交于点(0,3).
联系:y=2x+3的图象可以看作是y=2x的图象向上平移3个长度单位得到.
y=2x
y=2x+3
新课讲解
y=2x
y=2x+3
(1)一次函数y=kx+b的图象是______
____,称它为直线y=kx+b.
(2)一次函数y=kx+b(k≠0)的图象可以看作由直线y=kx平移______个单位长度而得到.
当b>0时,向_____平移,
当b<0时,向_____平移.
一条
直线
|b|
上
下
归纳小结
一次函数y=kx+b表达式的平移公式
y=kx+b
y=kx+(b+m)
向上平移m个单位
向下平移m个单位
y=kx+(b-m)
上下平移:常数项b增加或减少
新课讲解
一次函数y=kx+b(k≠0)的图象是一条直线,因为两点确定一条直线,所以画一次函数的图象时,只要描出图象上的两点即可画出一条直线.
选哪两个点最简单?
一般选直线与坐标轴的两个交点.
新课讲解
画出一次函数y=-2x-3的图象.
解:当x=0时,y=-3;
当x=1时,y=-5.
在平面直角坐标系中描出两点A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数y=-2x-3的图象,如图所示.
A(0,-3)
B(1,-5)
y=-2x-3
【教材P125页】
新课讲解
y=-2x-3
y=2x+3
观察画出的一次函数y=2x+3,y=-2x-3的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗?
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
新课讲解
y=-2x-3
y=2x+3
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
对于y=-2x-3,当自变量x的取值由小变大时,对应的函数值y由大变小.
新课讲解
一般地,一次函数y=kx+b(k,b为常数,k≠0)具有如下性质:
新课讲解
图中描述了某一天小亮从家骑车去书店购书,然后又骑车回家的情况。你能说出小亮在路上的情形吗?
分析:小亮骑车离家的距离y是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.
【教材P126页】
新课讲解
解:第一段是从原点出发的线段OA. 从横坐标看出,小亮路上花了30min,当横坐标从0变化到30时,纵坐标均匀增加,这说明小亮从家出发匀速前进30min,到达书店.
第二段是与x轴平行的一条线段AB,当横坐标从30变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min.
新课讲解
第三段是与x轴有交点的线段BC.从横坐标看出,小亮路上花了40min.当横坐标从60变化到100时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
新课讲解
1.(1)将直线y=3x向下平移2个单位,得到直线____________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________.
y=3x-2
y=-x
【教材P127页】
新课讲解
2.过两点分别作出一次函数 和 的图象,并指出函数值如何随自变量的变化而变化?
当自变量x的取值由小变大时,对应的函数值y由小变大.
当自变量x的取值由小变大时,对应的函数值y由大变小.
【教材P127页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.下列函数中,y随x的增大而减小的函数是( )
A. y=2x+8 B. y=-2+4x C. y=-2x+8 D. y=4x
2.已知一次函数y=kx+b的图象如图所示,则k、b的符号是( )
A. k>0,b>0 B. k>0,b<0
C. k<0,b>0 D. k<0,b<0
C
B
课堂练习
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,-3),则k=_____,b=_____.
y=-2x
-2
-3
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
通过本课时的学习,需要我们掌握
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
课堂小结
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 一次函数的图象和性质
课堂小结
第四章 一次函数 4.3
一次函数的图象
4.3.2 一次函数的图象与性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.函数图象概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
2.一次函数的解析式:
y=kx+b(k≠0)
3.正比例函数的解析式:
y=kx(k≠0)
新课导入
4.作函数图象有几个步骤?
列表
描点
连线
5.正比例函数图象有什么特点?
正比例函数y=kx(k为常数,k≠0)的图象是经过点(0,0)和点(1,k)的一条直线,直线上的点与y=kx对应的x、y的值一一对应.
当k>0时,图象过一、三象限,y随x的增大而增大;
当k<0时,图象过二、四象限,y随x的增大而减小.
新课导入
思考
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?它们图象之间有什么关系?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在平面直角坐标系中,先画出函数y=2x的图象,然后探索y=2x+3的图象是什么样的图形,猜测y=2x+3的图象与y=2x的图象有什么关系?
先取自变量x的一些值,算出y=2x,y=2x+3对应的函数值,列成表格如下:
新课讲解
从上表可以看出,横坐标相同,y=2x+3的点的纵坐标比y=2x的点的纵坐标大3,于是将y=2x的图象向上平移3个单位,就得到y=2x+3的图象,如图所示.
y=2x
y=2x+3
新课讲解
观察两个函数图象发现:
相同点:都是一条直线;倾斜程度相同;y随x的增大而增大.
不同点:y=2x的图象过原点;y=2x+3的图象与y轴交于点(0,3).
联系:y=2x+3的图象可以看作是y=2x的图象向上平移3个长度单位得到.
y=2x
y=2x+3
新课讲解
y=2x
y=2x+3
(1)一次函数y=kx+b的图象是______
____,称它为直线y=kx+b.
(2)一次函数y=kx+b(k≠0)的图象可以看作由直线y=kx平移______个单位长度而得到.
当b>0时,向_____平移,
当b<0时,向_____平移.
一条
直线
|b|
上
下
归纳小结
一次函数y=kx+b表达式的平移公式
y=kx+b
y=kx+(b+m)
向上平移m个单位
向下平移m个单位
y=kx+(b-m)
上下平移:常数项b增加或减少
新课讲解
一次函数y=kx+b(k≠0)的图象是一条直线,因为两点确定一条直线,所以画一次函数的图象时,只要描出图象上的两点即可画出一条直线.
选哪两个点最简单?
一般选直线与坐标轴的两个交点.
新课讲解
画出一次函数y=-2x-3的图象.
解:当x=0时,y=-3;
当x=1时,y=-5.
在平面直角坐标系中描出两点A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数y=-2x-3的图象,如图所示.
A(0,-3)
B(1,-5)
y=-2x-3
【教材P125页】
新课讲解
y=-2x-3
y=2x+3
观察画出的一次函数y=2x+3,y=-2x-3的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗?
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
新课讲解
y=-2x-3
y=2x+3
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
对于y=-2x-3,当自变量x的取值由小变大时,对应的函数值y由大变小.
新课讲解
一般地,一次函数y=kx+b(k,b为常数,k≠0)具有如下性质:
新课讲解
图中描述了某一天小亮从家骑车去书店购书,然后又骑车回家的情况。你能说出小亮在路上的情形吗?
分析:小亮骑车离家的距离y是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.
【教材P126页】
新课讲解
解:第一段是从原点出发的线段OA. 从横坐标看出,小亮路上花了30min,当横坐标从0变化到30时,纵坐标均匀增加,这说明小亮从家出发匀速前进30min,到达书店.
第二段是与x轴平行的一条线段AB,当横坐标从30变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min.
新课讲解
第三段是与x轴有交点的线段BC.从横坐标看出,小亮路上花了40min.当横坐标从60变化到100时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
新课讲解
1.(1)将直线y=3x向下平移2个单位,得到直线____________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________.
y=3x-2
y=-x
【教材P127页】
新课讲解
2.过两点分别作出一次函数 和 的图象,并指出函数值如何随自变量的变化而变化?
当自变量x的取值由小变大时,对应的函数值y由小变大.
当自变量x的取值由小变大时,对应的函数值y由大变小.
【教材P127页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.下列函数中,y随x的增大而减小的函数是( )
A. y=2x+8 B. y=-2+4x C. y=-2x+8 D. y=4x
2.已知一次函数y=kx+b的图象如图所示,则k、b的符号是( )
A. k>0,b>0 B. k>0,b<0
C. k<0,b>0 D. k<0,b<0
C
B
课堂练习
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,-3),则k=_____,b=_____.
y=-2x
-2
-3
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
通过本课时的学习,需要我们掌握
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
课堂小结
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 一次函数的图象和性质
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
