湘教版初中八年级下册数学 5.1 频数与频率 课件(共30张PPT)
文档属性
| 名称 | 湘教版初中八年级下册数学 5.1 频数与频率 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 07:28:10 | ||
图片预览





文档简介
(共30张PPT)
第五章 数据的频数分布 5.1
频数与频率
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
射击运动员进行射击训练,教练员需要根据前一阶段的得分情况进行分析,这就需要用到频数和频数直方图.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
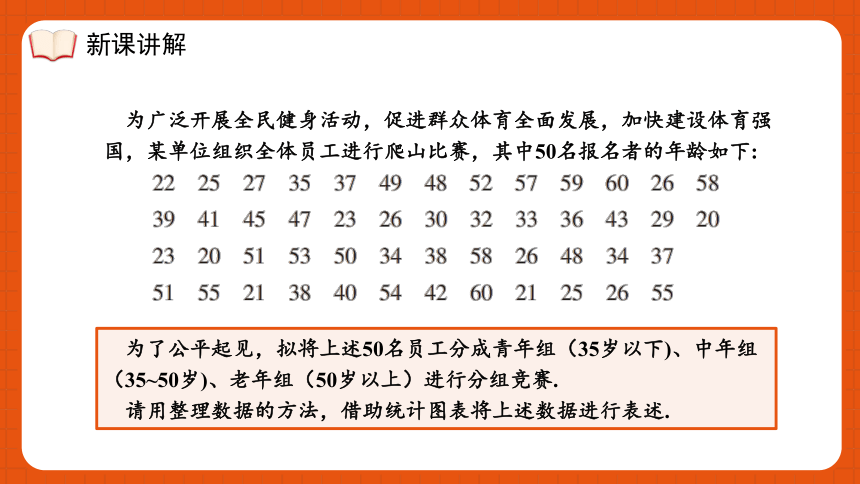
为广泛开展全民健身活动,促进群众体育全面发展,加快建设体育强国,某单位组织全体员工进行爬山比赛,其中50名报名者的年龄如下:
为了公平起见,拟将上述50名员工分成青年组(35岁以下)、中年组(35~50岁)、老年组(50岁以上)进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
新课讲解
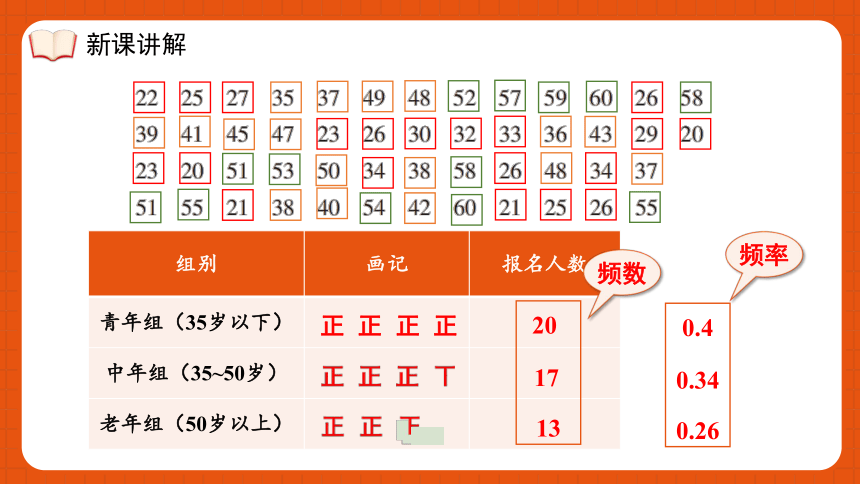
组别 画记 报名人数
青年组(35岁以下)
中年组(35~50岁)
老年组(50岁以上)
正 正 正 正
20
17
13
频数
0.4
0.34
0.26
频率
新课讲解
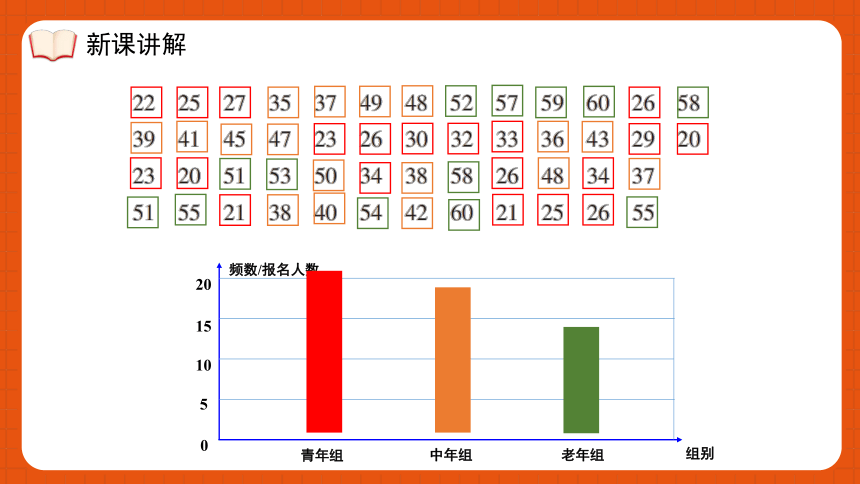
频数/报名人数
组别
青年组
中年组
老年组
0
5
10
15
20
新课讲解
小芳参加校射击队,在一次射击训练中,她先射击了15次,教练对其射击方法作了一些指导后,又射击了15次.她两次射击得分情况如下表所示:
【教材P149】
新课讲解
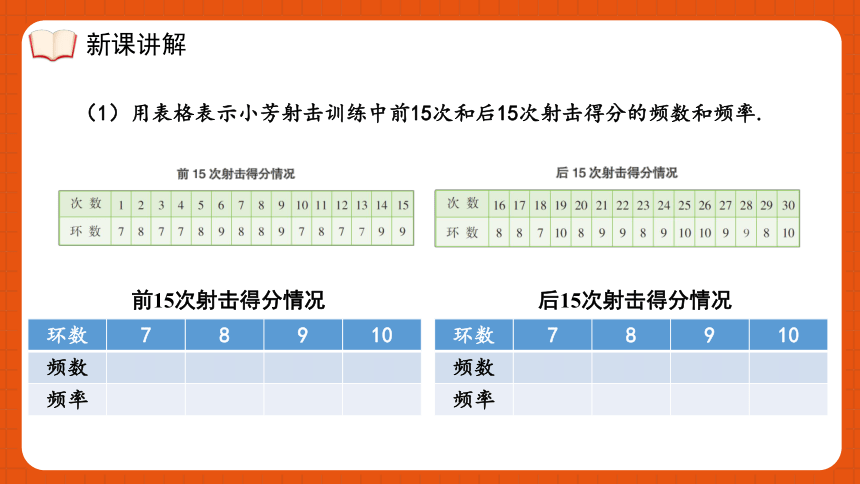
(1)用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
前15次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.33 0.27
后15次射击得分情况
新课讲解
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.33 0.27
前15次射击得分情况
后15次射击得分情况
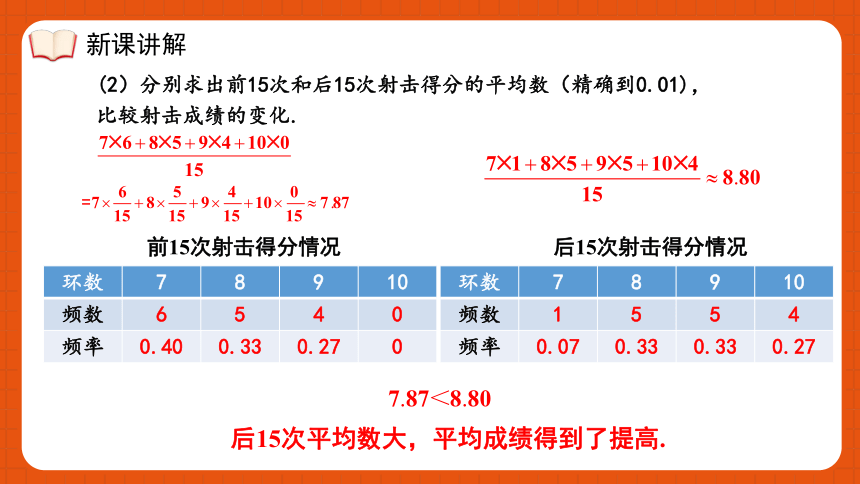
(2)分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
后15次平均数大,平均成绩得到了提高.
新课讲解
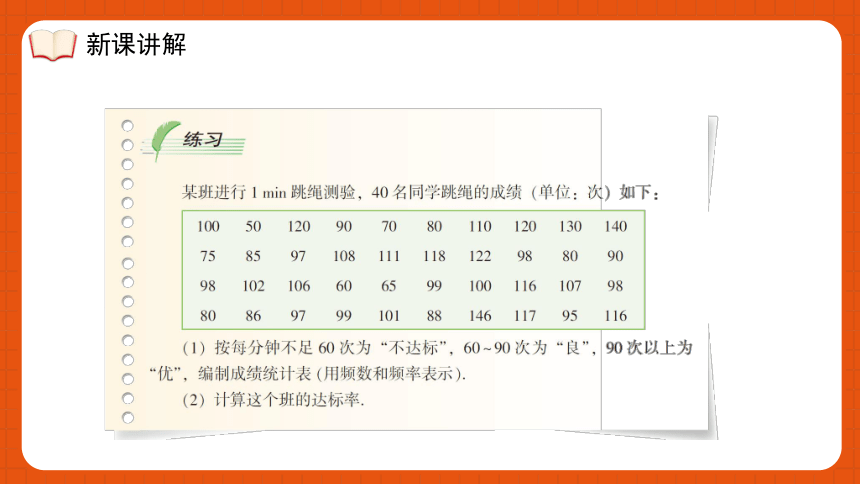
新课讲解
次数 不达标 良 优
频数 1 12 27
频率 0.025 0.3 0.675
(1)
(2)
39÷40=0.975
答:达标率是0.975.
新课讲解
一枚硬币有两面,我们称有国徽的一面为“正面”,另一面为“反面”.掷一枚硬币,当硬币落在桌面时,可能出现“正面朝上”,也可能出现“反面朝上” .每次掷币,两种情形必然出现一种,也只能出现一种.究竟出现哪种情形,在掷币之前无法预测,只有掷币之后才能知道.
新课讲解
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1)计算“正面朝上”和“反面朝上”的频数各是多少,它们之间有什么关系?
(2)计算“正面朝上”和“反面朝上”的频率各是多少,它们之间有什么关系?
新课讲解
假设某同学掷10次硬币的结果如下:
次 数 1 2 3 4 5 6 7 8 9 10
结 果 反 正 正 正 反 反 反 正 反 反
结果 正 反
频数 4 6
频率 0.4 0.6
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
新课讲解
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A.两枚硬币都是“正面朝上”;
B.两枚硬币都是“反面朝上”;
C.一枚硬币“正面朝上”,另一枚硬币“反面朝上”.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
现在全班同学每人各掷两枚硬币5次,记录所得结果,将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
课堂练习
课堂练习
课堂练习
1.某中学八年级(2)班40名同学投票选举班长,候选人包括陈佳、彭晓、黄敏和汤伟四位.为了方便记录,他们的得票分别以C,P,H,T来代表,投票结果如下:
(1)请根据上述投票结果完成下表:
8
11
9
12
0.2
0.275
0.225
0.3
(选自教材P153习题5.1)
课堂练习
(2)如果得票最高的候选人被选为班长,则四人中哪一位会当选?
8
11
9
12
0.2
0.275
0.225
0.3
汤伟会当选.
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(1)计算这些车的平均车速.
(40×20+45×30+48×40+50×10+52×10)÷(20+30+40+10+10)
≈46.3(km/h)
(选自教材P154习题5.1)
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(2)以哪一个速度行驶的车辆最多?以不超过50km/h的速度行驶的汽车占总监测量的百分之几?
(20+30+40+10)÷(20+30+40+10+10)≈90.9%
(选自教材P154习题5.1)
答:车速是48km/h的车最多,不超过50km/h的占总监测量的90.9%.
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(3)若要对该隧道的通行速度进行限制,你有什么好的建议?
车辆限速45~48km/h(答案不唯一,可根据实际情况确定).
(选自教材P154习题5.1)
课堂练习
3.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(1)上表中m=_______, n=______.
(2)在这次抽样调查中,哪类读物最受学生欢迎?哪类读物受欢迎程度最少?
84
0.33
0.14
200
28
(选自教材P154习题5.1)
0.33
84
课堂练习
3.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(3)若学校计划购买3000册图书,你对购书计划能提出什么好的建议吗?
购书计划:文学类购买3000×0.42=1260(册);
艺术类购买3000×0.11=330(册);
科普类购买3000×0.33=990(册);其他类购买3000-1260-330-990=420(册).
(选自教材P154习题5.1)
0.14
200
28
0.33
84
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第五章 数据的频数分布 5.1
频数与频率
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
射击运动员进行射击训练,教练员需要根据前一阶段的得分情况进行分析,这就需要用到频数和频数直方图.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
为广泛开展全民健身活动,促进群众体育全面发展,加快建设体育强国,某单位组织全体员工进行爬山比赛,其中50名报名者的年龄如下:
为了公平起见,拟将上述50名员工分成青年组(35岁以下)、中年组(35~50岁)、老年组(50岁以上)进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
新课讲解
组别 画记 报名人数
青年组(35岁以下)
中年组(35~50岁)
老年组(50岁以上)
正 正 正 正
20
17
13
频数
0.4
0.34
0.26
频率
新课讲解
频数/报名人数
组别
青年组
中年组
老年组
0
5
10
15
20
新课讲解
小芳参加校射击队,在一次射击训练中,她先射击了15次,教练对其射击方法作了一些指导后,又射击了15次.她两次射击得分情况如下表所示:
【教材P149】
新课讲解
(1)用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
前15次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.33 0.27
后15次射击得分情况
新课讲解
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.33 0.27
前15次射击得分情况
后15次射击得分情况
(2)分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
后15次平均数大,平均成绩得到了提高.
新课讲解
新课讲解
次数 不达标 良 优
频数 1 12 27
频率 0.025 0.3 0.675
(1)
(2)
39÷40=0.975
答:达标率是0.975.
新课讲解
一枚硬币有两面,我们称有国徽的一面为“正面”,另一面为“反面”.掷一枚硬币,当硬币落在桌面时,可能出现“正面朝上”,也可能出现“反面朝上” .每次掷币,两种情形必然出现一种,也只能出现一种.究竟出现哪种情形,在掷币之前无法预测,只有掷币之后才能知道.
新课讲解
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1)计算“正面朝上”和“反面朝上”的频数各是多少,它们之间有什么关系?
(2)计算“正面朝上”和“反面朝上”的频率各是多少,它们之间有什么关系?
新课讲解
假设某同学掷10次硬币的结果如下:
次 数 1 2 3 4 5 6 7 8 9 10
结 果 反 正 正 正 反 反 反 正 反 反
结果 正 反
频数 4 6
频率 0.4 0.6
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
新课讲解
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A.两枚硬币都是“正面朝上”;
B.两枚硬币都是“反面朝上”;
C.一枚硬币“正面朝上”,另一枚硬币“反面朝上”.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
现在全班同学每人各掷两枚硬币5次,记录所得结果,将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
课堂练习
课堂练习
课堂练习
1.某中学八年级(2)班40名同学投票选举班长,候选人包括陈佳、彭晓、黄敏和汤伟四位.为了方便记录,他们的得票分别以C,P,H,T来代表,投票结果如下:
(1)请根据上述投票结果完成下表:
8
11
9
12
0.2
0.275
0.225
0.3
(选自教材P153习题5.1)
课堂练习
(2)如果得票最高的候选人被选为班长,则四人中哪一位会当选?
8
11
9
12
0.2
0.275
0.225
0.3
汤伟会当选.
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(1)计算这些车的平均车速.
(40×20+45×30+48×40+50×10+52×10)÷(20+30+40+10+10)
≈46.3(km/h)
(选自教材P154习题5.1)
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(2)以哪一个速度行驶的车辆最多?以不超过50km/h的速度行驶的汽车占总监测量的百分之几?
(20+30+40+10)÷(20+30+40+10+10)≈90.9%
(选自教材P154习题5.1)
答:车速是48km/h的车最多,不超过50km/h的占总监测量的90.9%.
课堂练习
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(3)若要对该隧道的通行速度进行限制,你有什么好的建议?
车辆限速45~48km/h(答案不唯一,可根据实际情况确定).
(选自教材P154习题5.1)
课堂练习
3.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(1)上表中m=_______, n=______.
(2)在这次抽样调查中,哪类读物最受学生欢迎?哪类读物受欢迎程度最少?
84
0.33
0.14
200
28
(选自教材P154习题5.1)
0.33
84
课堂练习
3.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(3)若学校计划购买3000册图书,你对购书计划能提出什么好的建议吗?
购书计划:文学类购买3000×0.42=1260(册);
艺术类购买3000×0.11=330(册);
科普类购买3000×0.33=990(册);其他类购买3000-1260-330-990=420(册).
(选自教材P154习题5.1)
0.14
200
28
0.33
84
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
