湘教版初中八年级下册数学 第四章 一次函数 小结与复习 课件(共30张PPT)
文档属性
| 名称 | 湘教版初中八年级下册数学 第四章 一次函数 小结与复习 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
第四章 一次函数
小结与复习
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
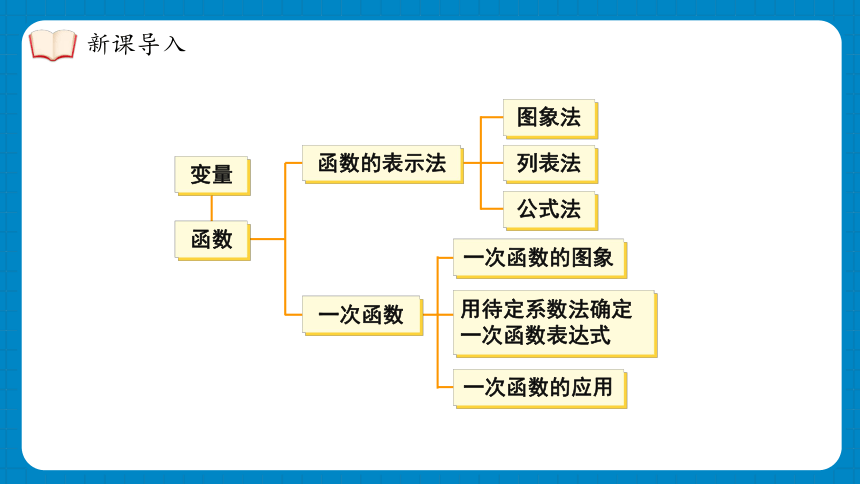
变量
函数
函数的表示法
一次函数
列表法
图象法
公式法
一次函数的图象
用待定系数法确定一次函数表达式
一次函数的应用
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.一次函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k_____),那么y叫做x的一次函数.
kx+b
≠0
特别地,当b____时,函数y=____(k____)叫做正比例函数.
kx
=0
≠0
★理解一次函数概念应注意下面两点:
⑴自变量x的次数是___次,
⑵比例系数_____.
1
≠0
新课讲解
例1.若y=(m-1)x|m|+1是一次函数,则m的值为______.
【解析】本题考查一次函数的概念.由一次函数的概念可知表达式中自变量x的次数是1次,故|m|=1,所以m=±1,又因为m-1≠0,所以m=-1.
-1
新课讲解
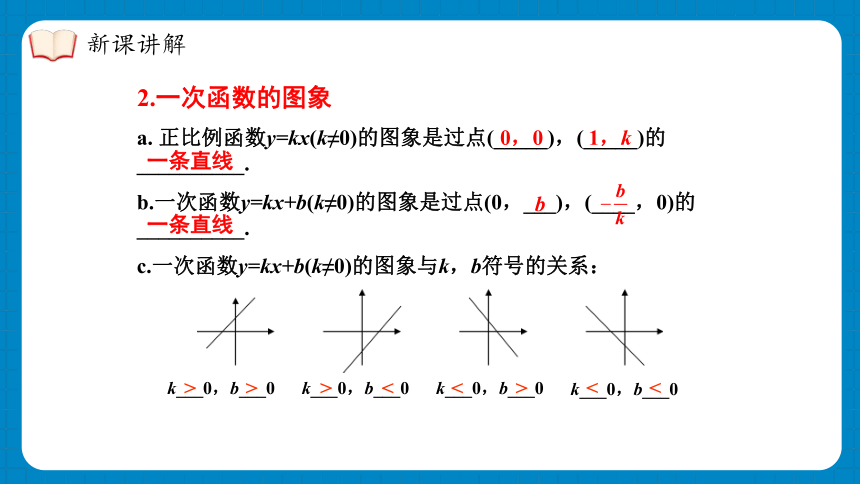
2.一次函数的图象
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(_____)的__________.
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________.
0,0
1,k
一条直线
b
一条直线
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
>
>
<
<
>
<
<
新课讲解
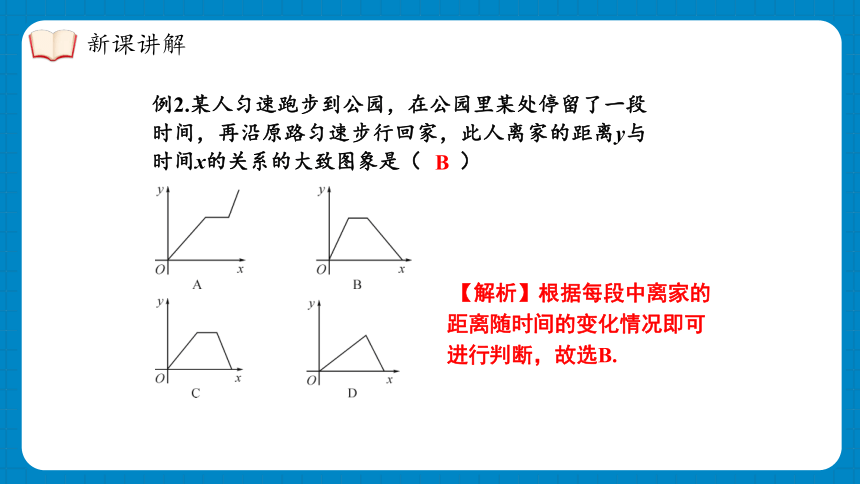
例2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
【解析】根据每段中离家的距离随时间的变化情况即可进行判断,故选B.
B
新课讲解
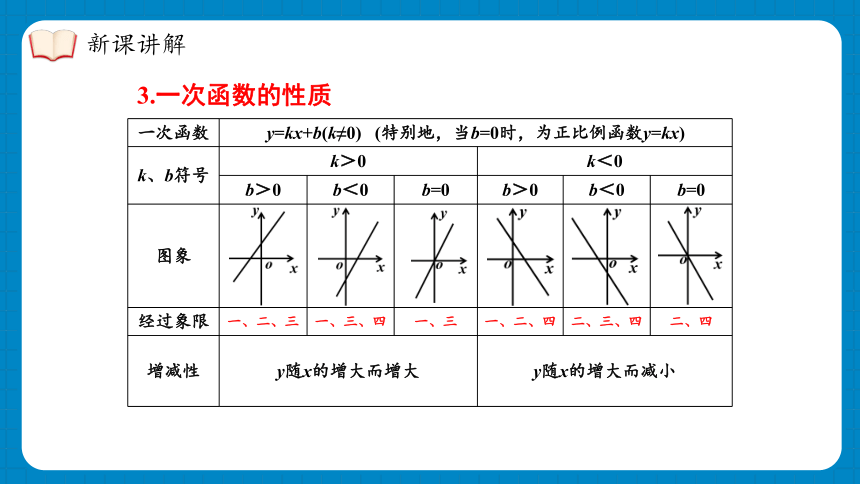
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 3.一次函数的性质
新课讲解
例3. (1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
【解析】(1)因为k=2>0,所以由正比例函数的性质可知,它的图象经过第一、三象限,y随x的增大而增大;(2)y=(2m-1)xm -3是正比例函数的条件是m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这些条件得:当m2-3=1,2m-1<0时, y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,故(1)一、三;增大;(2)-2.
一、三
增大
-2
新课讲解
4.一次函数的应用
(1)待定系数法:
①设这个函数表达式为y=kx+b;
②把已知点的坐标x,y的对应值代入表达式列出方程组;
③解这个二元一次方程组,求出k、b的值;
④把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
新课讲解
(2)利用一次函数解决实际问题:
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.验证并化简函数表达式,得出问题的变化规律.
新课讲解
例4.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
新课讲解
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:货车的速度V货=300÷5=60(千米/时),由图象可知货车比轿车迟到0.5小时,∴此时货车距乙地的路程为0.5×60=30(千米);
新课讲解
(2)求线段CD对应的函数表达式.
解:设CD段函数表达式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴2.5k+b=80,4.5k+b=300,解得k=110,b=-195.
∴CD段函数表达式为:y=110x-195(2.5≤x≤4.5);
新课讲解
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,
∵v货车=60千米/时,
v轿车=(300-80)÷(4.5-2.5)=110(千米/时)
∴110(x-4.5)+60x=300,解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.某型号体温计中,刻度为35 ℃处,水银柱长2.5 cm.体温每升高1 ℃,水银柱就伸长0.7 cm.
(1)求水银柱长y(cm) 随体温x(℃) 而变化的函数表达式,其中35≤x≤42. 这是不是一次函数?画出它的图象.
(2)分别求当体温为37 ℃,38.6 ℃时,水银柱长多少?
课堂练习
(1)解:y=2.5+(x-35)·0.7=0.7x-22(35≤x≤42),是一次函数.
(2)解:当x=37时,y=3.9;
当x=38.6时,y=5.02.
课堂练习
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
解:图象法:与x轴的交点分别为(-6,0),( ,0),( ,0).
课堂练习
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
公式法:令 x+3=0,解得x=-6.令2x-1=0,解得x= .令-3x+5=0,解得x= .所以它们与x轴的交点坐标分别是(-6,0),( ,0),( ,0).
课堂练习
3.某公司急需租一辆汽车,甲汽车出租公司的出租条件为每千米的租车费为2 元,乙汽车出租公司的条件是每月需支付固定租金800 元,另外每千米的租车费为1.2 元. 若设汽车行驶路程为x(km),租用甲公司的费用为y1(元),租用乙公司的费用为y2(元).
(1)分别写出y1,y2随x而变化的函数表达式;
(2)在1 个月内,当汽车行驶路程超过多少千米时, 租用乙公司的汽车较合算?
课堂练习
(1)解:y1=2x(x≥0);y2=800+1.2x (x≥0)
y1=2x
y2=800+1.2x
(2)解:分别画出函数y1=2x(x≥0)与y2=800+1.2x (x≥0)图象如下图所示,由图象可知当汽车行驶路程超过1000km时, 租用乙公司的汽车较合算.
课堂练习
4.某城市的一种出租汽车,当行驶路程小于3 km时,车费都为10 元;大于或等于3 km,但小于15 km时,超过3 km 的那部分路程每千米收费1.6 元;大于或等于15 km 时,超过15 km 的那部分每千米收费2.4元. 乘客为了估算应付的车费, 需要一个较简单的计费公式.
课堂练习
(1)你能给出估算车费y(元)与行驶路程x(km)之间的函数表达式吗?
解:由题意得出:当行驶路小于3km时,车费都为10元;则y=10(0<x<3);当大于或等于3km但小于15km时,超过3km的那部分路程每千米收费1.6元;则y=10+1.6(x-3)(3≤x<15);当大于或等于15km时,超过15km的那部分每千米收费2.4元,则y=10+1.6(15-3)+2.4(x-15)=29.2+2.4(x-15)(x≥15),
综上所述
课堂练习
(2)画出这个函数的图象;
课堂练习
(3)当行驶路程为30 km时, 估算车费是多少?
解:当行驶路程为30km时,车费是:
29.2+2.4×(30-15)=65.2(元).
答:当行驶路程为30 km时, 估算车费是65.2元.
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课堂小结
第四章 一次函数
小结与复习
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
变量
函数
函数的表示法
一次函数
列表法
图象法
公式法
一次函数的图象
用待定系数法确定一次函数表达式
一次函数的应用
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.一次函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k_____),那么y叫做x的一次函数.
kx+b
≠0
特别地,当b____时,函数y=____(k____)叫做正比例函数.
kx
=0
≠0
★理解一次函数概念应注意下面两点:
⑴自变量x的次数是___次,
⑵比例系数_____.
1
≠0
新课讲解
例1.若y=(m-1)x|m|+1是一次函数,则m的值为______.
【解析】本题考查一次函数的概念.由一次函数的概念可知表达式中自变量x的次数是1次,故|m|=1,所以m=±1,又因为m-1≠0,所以m=-1.
-1
新课讲解
2.一次函数的图象
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(_____)的__________.
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________.
0,0
1,k
一条直线
b
一条直线
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
>
>
<
<
>
<
<
新课讲解
例2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
【解析】根据每段中离家的距离随时间的变化情况即可进行判断,故选B.
B
新课讲解
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 3.一次函数的性质
新课讲解
例3. (1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
【解析】(1)因为k=2>0,所以由正比例函数的性质可知,它的图象经过第一、三象限,y随x的增大而增大;(2)y=(2m-1)xm -3是正比例函数的条件是m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这些条件得:当m2-3=1,2m-1<0时, y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,故(1)一、三;增大;(2)-2.
一、三
增大
-2
新课讲解
4.一次函数的应用
(1)待定系数法:
①设这个函数表达式为y=kx+b;
②把已知点的坐标x,y的对应值代入表达式列出方程组;
③解这个二元一次方程组,求出k、b的值;
④把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
新课讲解
(2)利用一次函数解决实际问题:
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.验证并化简函数表达式,得出问题的变化规律.
新课讲解
例4.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
新课讲解
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:货车的速度V货=300÷5=60(千米/时),由图象可知货车比轿车迟到0.5小时,∴此时货车距乙地的路程为0.5×60=30(千米);
新课讲解
(2)求线段CD对应的函数表达式.
解:设CD段函数表达式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴2.5k+b=80,4.5k+b=300,解得k=110,b=-195.
∴CD段函数表达式为:y=110x-195(2.5≤x≤4.5);
新课讲解
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,
∵v货车=60千米/时,
v轿车=(300-80)÷(4.5-2.5)=110(千米/时)
∴110(x-4.5)+60x=300,解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.某型号体温计中,刻度为35 ℃处,水银柱长2.5 cm.体温每升高1 ℃,水银柱就伸长0.7 cm.
(1)求水银柱长y(cm) 随体温x(℃) 而变化的函数表达式,其中35≤x≤42. 这是不是一次函数?画出它的图象.
(2)分别求当体温为37 ℃,38.6 ℃时,水银柱长多少?
课堂练习
(1)解:y=2.5+(x-35)·0.7=0.7x-22(35≤x≤42),是一次函数.
(2)解:当x=37时,y=3.9;
当x=38.6时,y=5.02.
课堂练习
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
解:图象法:与x轴的交点分别为(-6,0),( ,0),( ,0).
课堂练习
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
公式法:令 x+3=0,解得x=-6.令2x-1=0,解得x= .令-3x+5=0,解得x= .所以它们与x轴的交点坐标分别是(-6,0),( ,0),( ,0).
课堂练习
3.某公司急需租一辆汽车,甲汽车出租公司的出租条件为每千米的租车费为2 元,乙汽车出租公司的条件是每月需支付固定租金800 元,另外每千米的租车费为1.2 元. 若设汽车行驶路程为x(km),租用甲公司的费用为y1(元),租用乙公司的费用为y2(元).
(1)分别写出y1,y2随x而变化的函数表达式;
(2)在1 个月内,当汽车行驶路程超过多少千米时, 租用乙公司的汽车较合算?
课堂练习
(1)解:y1=2x(x≥0);y2=800+1.2x (x≥0)
y1=2x
y2=800+1.2x
(2)解:分别画出函数y1=2x(x≥0)与y2=800+1.2x (x≥0)图象如下图所示,由图象可知当汽车行驶路程超过1000km时, 租用乙公司的汽车较合算.
课堂练习
4.某城市的一种出租汽车,当行驶路程小于3 km时,车费都为10 元;大于或等于3 km,但小于15 km时,超过3 km 的那部分路程每千米收费1.6 元;大于或等于15 km 时,超过15 km 的那部分每千米收费2.4元. 乘客为了估算应付的车费, 需要一个较简单的计费公式.
课堂练习
(1)你能给出估算车费y(元)与行驶路程x(km)之间的函数表达式吗?
解:由题意得出:当行驶路小于3km时,车费都为10元;则y=10(0<x<3);当大于或等于3km但小于15km时,超过3km的那部分路程每千米收费1.6元;则y=10+1.6(x-3)(3≤x<15);当大于或等于15km时,超过15km的那部分每千米收费2.4元,则y=10+1.6(15-3)+2.4(x-15)=29.2+2.4(x-15)(x≥15),
综上所述
课堂练习
(2)画出这个函数的图象;
课堂练习
(3)当行驶路程为30 km时, 估算车费是多少?
解:当行驶路程为30km时,车费是:
29.2+2.4×(30-15)=65.2(元).
答:当行驶路程为30 km时, 估算车费是65.2元.
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
