专项1 单项选择2(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项1 单项选择2(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 663.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览


文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项1 单项选择2(浙江中考真题+中考模拟)
一、选择题
1.(2024·浙江)2024年浙江经济一季度GDP为201370000万元,其中201370000用科学记数法表示为( )
A. B.
C. D.
2.(2025·衢州模拟)计算:( )
A. B.3a C. D.3
3.(2024·浙江)有编号分别为的8个球,其中6个球一样重,另外两个都轻1克,为了找出这两个轻球,用天平称了三次:第一次比重,第二次比轻,第三次和一样重,则两个轻球的编号应该是( )
A.④⑤ B.③⑥ C.③⑤ D.③④
4.(2025·衢江模拟)(我国古代算题)马四匹,牛六头,共价四十八两(我国古代货币单位);马三匹,牛五头,共价三十八两.问马,牛各价几何?设马价为每匹两,牛价为每头两,则可列方程组为( )
A. B.
C. D.
5.(2025·鹿城模拟)小明在学习了勾股定理的证明后,尝试制作了四个全等三角形纸板,并拼出一个新图形,如图所示,若,则正方形的周长为( )
A.14 B.17 C.20 D.24
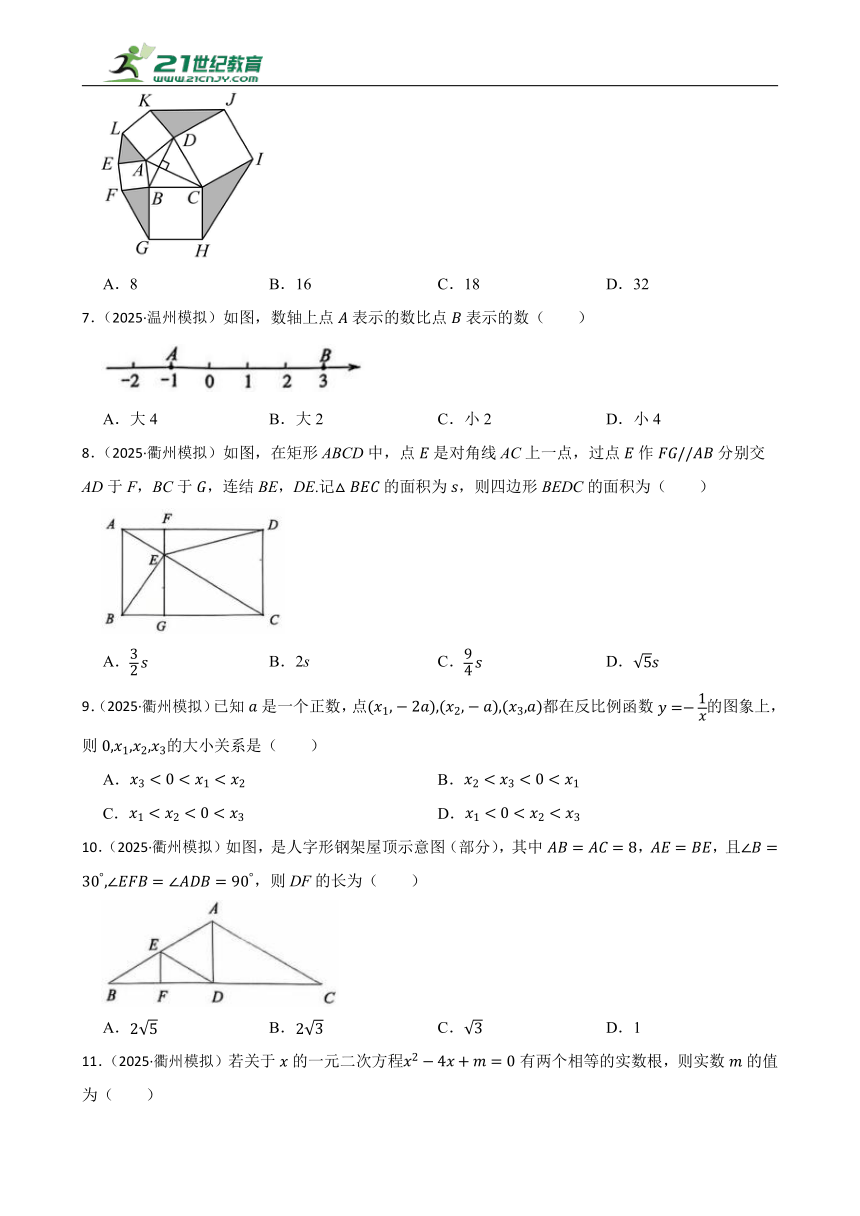
6.(2024·浙江)如图,在四边形中,,且,分别以四边形的四条边为边向形外作正方形、正方形、正方形、正方形,则图中各阴影部分面积和的最大值为( )
A.8 B.16 C.18 D.32
7.(2025·温州模拟)如图,数轴上点表示的数比点表示的数( )
A.大4 B.大2 C.小2 D.小4
8.(2025·衢州模拟)如图,在矩形ABCD中,点是对角线AC上一点,过点作分别交AD于F,BC于,连结BE,DE.记的面积为,则四边形BEDC的面积为( )
A. B.2s C. D.
9.(2025·衢州模拟)已知是一个正数,点都在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
10.(2025·衢州模拟)如图,是人字形钢架屋顶示意图(部分),其中,,且,则DF的长为( )
A. B. C. D.1
11.(2025·衢州模拟)若关于的一元二次方程有两个相等的实数根,则实数的值为( )
A.-16 B.-4 C.4 D.16
12.(2025·衢州模拟)因式分解:( )
A. B.
C. D.
13.(2025·衢州模拟)如图,在平面直角坐标系中,线段与线段AB是位似图形,位似中心为点.已知点的坐标分别为.若,则点的对应点的坐标是( )
A. B. C. D.
14.(2025·衢州模拟)某高速路段上的一台机动车雷达测速仪记录了一段时间内通过的九辆机动车速度,数据如下(单位:千米/时):100,96,86,77,96,93,108,96,95.这组数据的中位数是( )
A.96.5 B.96 C.95.5 D.94.5
15.(2025·衢州模拟)如图,点是正方形网格中的格点,点是以为圆心的圆与网格线的交点,直线经过点与点,则点关于直线的对称点是( )
A. B. C. D.
16.(2025·衢州模拟)下列四个数中,最小的数是( )
A.-2 B.-1 C.0 D.5
17.(2025·鹿城模拟)如图,在中,,设,,且是定值,点是上一点,点为中点,连接,将线段沿绕点顺时针旋转,得到线段交于点,若点关于直线的对称点恰为点,则下列线段长为定值的是( )
A. B. C. D.
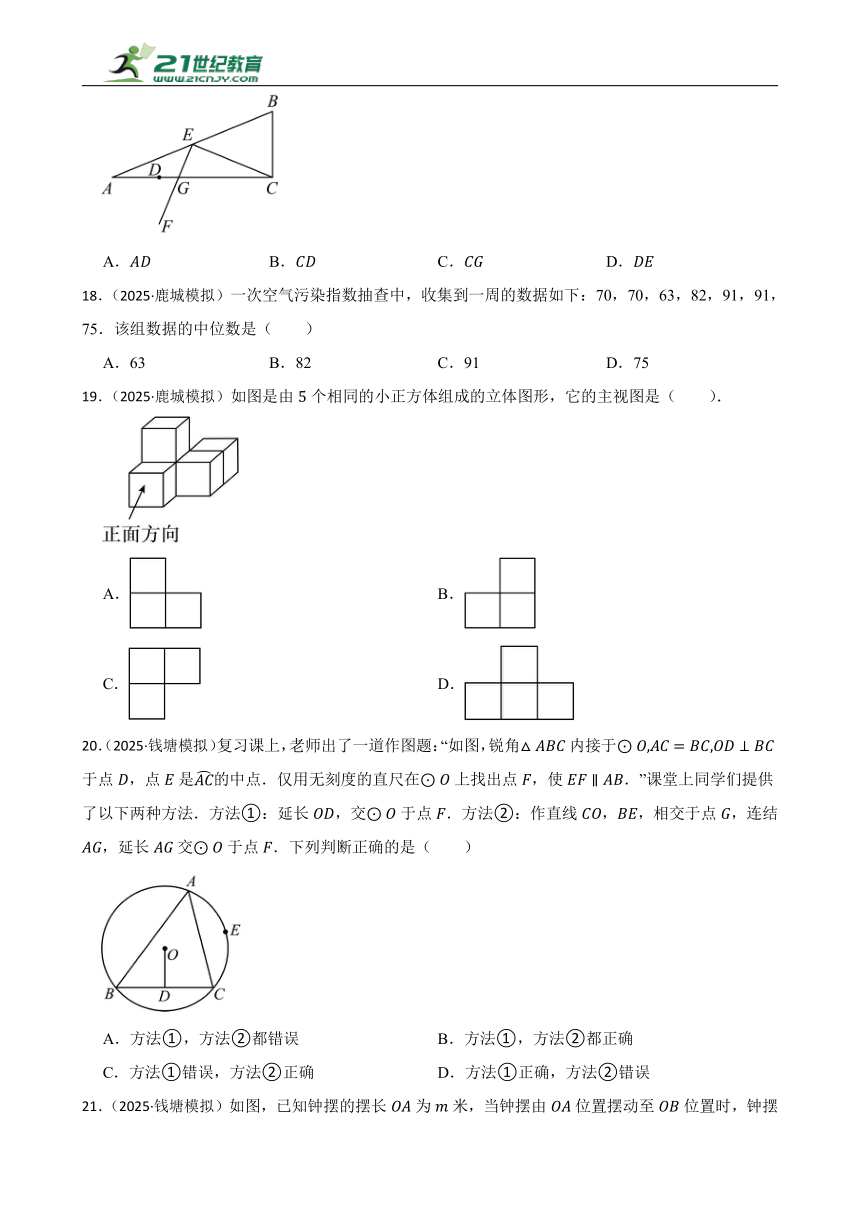
18.(2025·鹿城模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
19.(2025·鹿城模拟)如图是由个相同的小正方体组成的立体图形,它的主视图是( ).
A. B.
C. D.
20.(2025·钱塘模拟)复习课上,老师出了一道作图题:“如图,锐角内接于于点,点是的中点.仅用无刻度的直尺在上找出点,使.”课堂上同学们提供了以下两种方法.方法①:延长,交于点.方法②:作直线,,相交于点,连结,延长交于点.下列判断正确的是( )
A.方法①,方法②都错误 B.方法①,方法②都正确
C.方法①错误,方法②正确 D.方法①正确,方法②错误
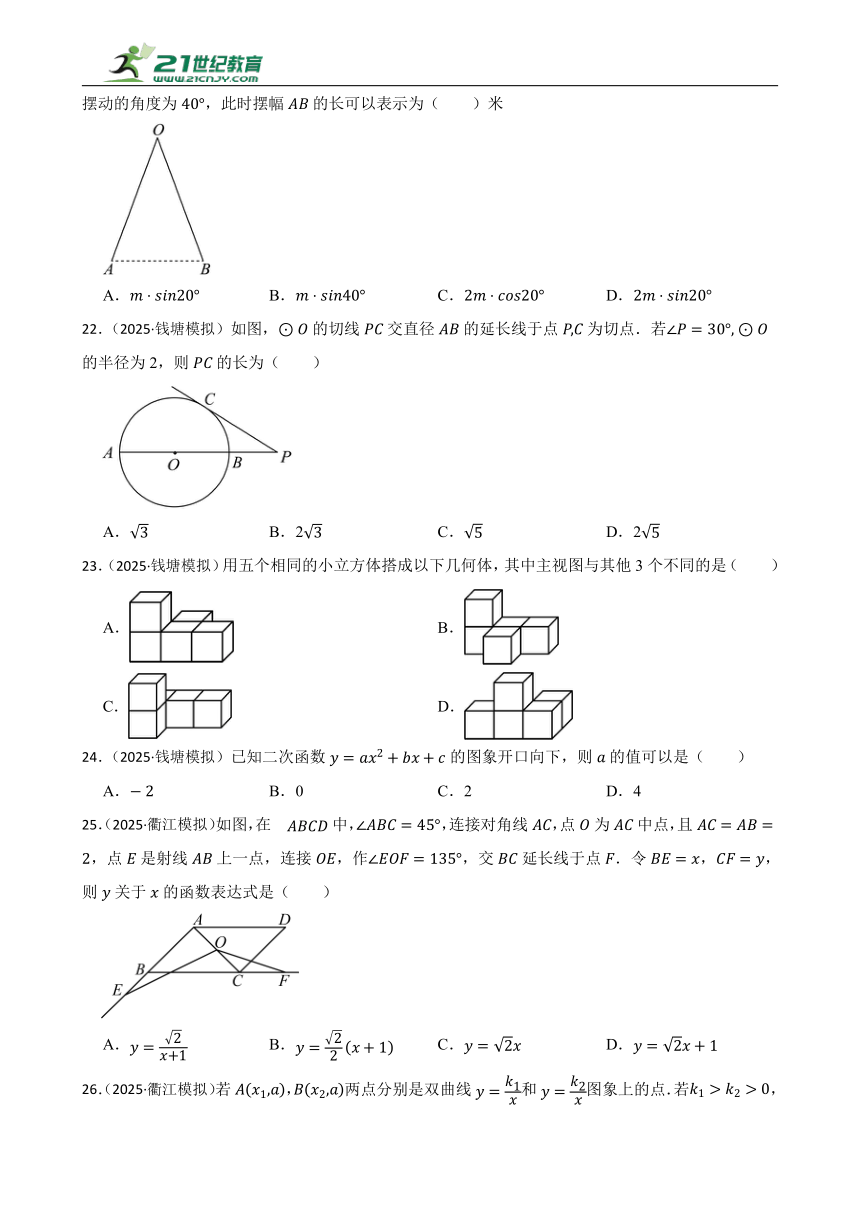
21.(2025·钱塘模拟)如图,已知钟摆的摆长为米,当钟摆由位置摆动至位置时,钟摆摆动的角度为,此时摆幅的长可以表示为( )米
A. B. C. D.
22.(2025·钱塘模拟)如图,的切线交直径的延长线于点为切点.若的半径为2,则的长为( )
A. B.2 C. D.2
23.(2025·钱塘模拟)用五个相同的小立方体搭成以下几何体,其中主视图与其他3个不同的是( )
A. B.
C. D.
24.(2025·钱塘模拟)已知二次函数的图象开口向下,则的值可以是( )
A. B.0 C.2 D.4
25.(2025·衢江模拟)如图,在中,,连接对角线,点为中点,且,点是射线上一点,连接,作,交延长线于点.令,,则关于的函数表达式是( )
A. B. C. D.
26.(2025·衢江模拟)若,两点分别是双曲线和图象上的点.若,且,则和的大小为( )
A. B. C. D.
27.(2025·衢江模拟)如图,在直角坐标系中,的三个顶点分别为,,,现以原点为位似中心,在第一象限内作与的位似比为的位似图形,则点坐标为( )
A. B. C. D.
28.(2025·衢江模拟)下列式子的运算结果为的是( )
A. B. C. D.
29.(2025·衢江模拟)如图,已知两平行线、被直线所截,,则的度数为( )
A. B. C. D.
30.(2025·衢江模拟)下列各数中最大的数是( )
A.1 B.0 C. D.
31.(2025·镇海区模拟)已知二次函数的图象与轴没有交点,且,则( )
A. B. C. D.
32.(2025·镇海区模拟)已知矩形的顶点在半径为5的半圆上,顶点在直径上.若,则矩形的面积等于( )
A.22 B.23 C.24 D.25
33.(2025·镇海区模拟)在平面直角坐标系中,点一定位于( )
A.一次函数图象的上方 B.一次函数图象的下方
C.一次函数图象的上方 D.一次函数图象的下方
34.(2025·镇海区模拟)如图,在正方形中,将对角线绕点逆时针旋转角度,使得(为正实数).设.( )
A.若,则 B.若,则
C.若,则 D.若,则
35.(2025·镇海区模拟)已知一次函数的图象与反比例函数交于两点.当时,的面积为1,则当时,的面积为( )
A. B.1 C. D.2
36.(2025·镇海区模拟)如图,多边形是边长为1的正六边形,则( )
A. B. C. D.
37.(2025·镇海区模拟)我国“北斗导航系统”用的原子钟以纳秒级计算时间.已知1秒=1000000000纳秒,则数据1000000000用科学记数法可以表示为( )
A. B. C. D.
38.(2025·镇海区模拟)透过城市文旅LOGO可以窥见城市独有的文旅魅力.下列城市文旅LOGO是轴对称图形的是( )
A. B.
C. D.
39.(2025·金华模拟)下列运算中,不正确的是( )
A. B. C. D.
40.(2025·湖州模拟)中,,点,分别在边,上,连结,,,若,,,则的大小为( )
A. B. C. D.
41.(2025·湖州模拟)如图,在扇形中,,,过OB的中点C作交于点D,以C为圆心,的长为半径作弧交的延长线于点E,则图中阴影部分的面积为( )
A. B. C. D.
42.(2025·湖州模拟)与式子的值最接近的整数是( )
A.3 B.4 C.5 D.6
43.(2025·湖州模拟)计算结果为的是( )
A. B. C. D.
44.(2025·湖州模拟)按照国家统计局的数据,2024年中国生产芯片在4300亿颗以上,数据4300亿用科学记数法表示为( )
A. B. C. D.
45.(2025九下·东阳模拟)解不等式组:时,不等式①和不等式②的解集在数轴上表示正确的是( )
A. B.
C. D.
46.(2025九下·东阳模拟)如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以点O为位似中心的位似图形,且相似比为1:3,两个正方形在原点O同侧,点A、B、E在x轴上,其余顶点在第一象限,若正方形ABCD的边长为2,则点F的坐标( )
A.(9,6)
B.(3,2)
C.(6,9)
D.(2,3)
47.(2025九下·东阳模拟)下列运算正确的是( )
A.a3 a4=a12 B.(a2)3=a6 C.a6÷a3=a2 D.a3+a4=a7
48.(2025九下·东阳模拟)截止2025年2月23日15时26分。动画电影《哪吒之魔童闹海》累计票房(含预售)突破135亿,成为我国首部百亿电影!将数据“135亿”用科学记数法表示为( )
A.1.35×1011 B.13.5×1010 C.1.35×1010 D.1.35×109
49.(2025九下·东阳模拟)下列四个数中,最小的数是( )
A.0 B.-1 C.-2 D.-3
50.(2025九下·东阳模拟)下列选项中可以用来说明命题“若x2>1,则x>1”是假命题的反例是( )
A.x=1 B.x=-1 C.x=2 D.x=-2
答案解析部分
1.D
解:201370000=2.137×108.
故答案为:D.
根据科学记数法的表示形式为:a×10n,其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1
2.C
解:.
故答案为:C.
利用同分母分式相减法则计算.
3.A
4.D
解:由题意,可列方程组为:
;
故答案为:D.
根据题中的相等关系"四匹马的价格+六头牛的价格=四十八两,三匹马的价格+五头牛的价格=三十八两"列出关于x、y的方程组并结合各选项即可判断求解.
5.C
解:设每个三角形的长直角边为,短直角边为,
由题意可得,解得,
∴,
∴正方形的周长为,
故答案为:C.
设每个三角形的长直角边为,短直角边为,然后根据题意和图形可得关于a、b的方程组,解方程组求出的值,再根据勾股定理求得的长,最后根据正方形的周长边长计算即可求解.
6.B
7.D
解:
答案为:D.
数轴上右边的点表示的数字总比左边的点表示的数字大,其中大小差就是这两点之间的距离.
8.B
解:过点B作BM⊥AC于点M,过点D作DN⊥AC于点N,
∵四边形ABCD是矩形,
∴AB=CD,AB//CD,
∴∠BAM=∠DCN,
在△ABM与△CDN中,
,
∴△ABM≌△CDN(AAS),
∴BM=DN,
∵,
∴,
∴四边形BEDC的面积为2s.
故答案为:B.
先利用矩形的性质,证明△ABM≌△CDN,再根据全等三角形的性质,得出BM=DN,再利用三角形面积公式求解,从而求得四边形BEDC的面积.
9.A
解:∵ 点都在反比例函数的图象上,
∴
解得:
∵是一个正数,
∴
∴中最小,只有A符合.
故答案为:A.
先分别求得三个自变量的值,再根据a的符号来确定三个自变量的符号,然后利用排除法求解.
10.B
解:∵,,,
∴AE=BE=DE=4,
∵,
∴,
∴,解得:BF=.
又BE=DE,,
∴DF=BF=.
故答案为:B.
先根据直角三角形斜边上的中线的性质求得AE=BE=DE=4,再余弦求得BF,然后利用等腰三角形三线合一求得DF.
11.C
解:∵关于的一元二次方程有两个相等的实数根,
∴(-4)2-4m=0,解得:m=4.
故答案为:C.
根据一元二次方程有两个相等的实数根,列出关于m的方程求解.
12.D
解:.
故答案为:D.
利用平方差公式分解因式.
13.A
解:∵ 线段与线段AB是位似图形,位似中心为点 ,
∴OA':OA=OB':OB=A'B':AB,
∵ 点的坐标分别为,
∴A'B'=4-2=2.
又,
∴OA':OA=OB':OB=A'B':AB=2:3,
∴A的横坐标为2,纵坐标为3.
即A(3,).
故答案为:A.
先根据位似图形的性质,列出比例式,再求出A'B',结合AB=3求出位似比,再求出A点的坐标.
14.B
解:将数据从小到大排列为:77,86,93,95,96,96,96,100,108,所以中位数为.
故答案为:B.
先将数据从小到大排列,再求中位数.
15.D
解:∵PP4被直线m垂直平分,
∴关于直线的对称点是P4.
故答案为:D.
根据“关于一条直线对称的两个点的连线被这条直线垂直平分”求解.
16.A
解:将-2,-1,0,5从小到大排列为-2<-1<0<5,所以最小的数是-2.
故答案为:A.
先将四个数从小到大排列,再找出最小的数.
17.B
解:连接,,,在上取点H,使,连接,过点E作于点K,如图所示:
∵在中,,点为中点,
∴,
∴,
根据旋转可知:,,
∴和为等腰三角形,,
设,则,
∴,
∴,
根据轴对称可知:,,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,,
,
∴,
∴,
∴,
∴,
∴为的中位线,
∴,
∴、均不是定值,
∴,
∴为定值,
∵,,
∴,
∵,
∴,
∴,
∴,
∴为的中位线,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴不是定值,
综上分析可知,为定值.
故答案为:B.
连接,,,在上取点H,使,连接,过点E作于点K,根据直角三角形的性质得出,设,则,求出,得出,求出,得出,求出,,得出,求出,根据“平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例”可得比例式,结合比例式将AD=DK、ED用含x、y的代数式表示出来,由线段的和差将CD用含x、y的代数式表示出来,根据平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似可得△KEG∽△DFG,于是可得比例式,结合比例式可将DG用含x、y的代数式表示出来,由线段的和差将CG用含x、y的代数式表示出来即可求解.
18.D
解:将这组数据重新排序为:63,70,70,75,82, 91,91,
则其中位数为75,
故答案为:D.
中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数;根据中位数的定义并结合题意即可求解.
19.A
解:从正面看,底层是两个小正方形,第二层左边是一个小正方形,
故它的主视图是.
故答案为: .
根据主视图是从正面看得到的图形即可求解.
20.B
21.D
22.B
23.D
24.A
25.B
解:设交于点,过点作,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∵点为中点,
∴,,
∴,
∴,
∴,
∵,
∴,
∴,即:,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,即:,
∴;
故答案为:B.
设交于点,过点作,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的对应边的比相等可得比例式,同理可证,由相似三角形的对应边的比相等可得比例式,根据这个比例式可将BH用含x的代数式表示出来,根据“有两个角对应相等的两个三角形相似”可证,由相似三角形的对应边的比相等可得比例式,由比例式可得y与x之间的函数关系式.
26.A
解:将,两点分别代入和
得:,,
∴,,
∴,
∵,,
∴,
∴,
故答案为:A.
由题意,将,两点分别代入和可将x1、x2用含a、k1、k2的代数式表示出来,计算x1-x2的值,结合","即可判断符号,然后根据不等式的性质即可求解.
27.C
解:∵以原点为位似中心,在第一象限内作与的位似比为的位似图形,且点C的坐标为,
∴点坐标为,即:;
故答案为:C.
根据关于原点为位似中心的两个位似图形的对应点的坐标关系“横、纵坐标变为原来的2倍”计算即可求解.
28.D
解:A、∵,∴此选项不符合题意;
B、∵,∴此选项不符合题意;
C、∵,∴此选项不符合题意;
D、∵,∴此选项符合题意;
故答案为:D.
A、根据合并同类项法则“把同类项的系数相加,字母和字母的指数不变”可求解;
B、根据同底数幂的乘法法则“同底数幂相乘,底数不变,指数相加”可求解;
C、根据同底数幂的除法法则“同底数幂相除,底数不变,指数相减”可求解;
D、根据幂的乘方法则“幂的乘方,底数不变,指数相乘”可求解.
29.B
解:
∵,
∴,
∴;
故答案为:B.
根据平行线的性质“两直线平行,同位角相等”可得,再根据邻补角互补即可求解.
30.A
解:∵;
∴最大的数是1;
故答案为:A.
根据有理数大小的比较法则"负数小于0,0小于正数,两个负数,绝对值大的反而小"判断即可求解.
31.A
32.C
33.C
34.B
35.B
36.D
37.B
38.A
39.D
解:,故A正确;
,故B正确;
,故C正确;
,故D错误.
故答案为:D.
(1)利用合并同类项法则计算;
(2)利用同底数幂相乘法则计算;
(3)利用单项式除以单项式法则计算;
(4)利用幂的乘方法则计算.
40.D
41.D
42.B
43.C
44.C
45.C
解:由①得:x<2,
由②得:x≥-3,
∴此不等式组的解集为-3≤x<2,
此不等式组的解集在数轴上表示符合题意的是选项C.
故答案为:C.
分别求出不等式组中每一个不等式的解集,再确定出不等式组的解集,观察各选项,可得答案.
46.A
解:∵ 正方形ABCD与正方形BEFG是以点O为位似中心的位似图形,且相似比为1:3,
∴△ODC∽△OGF,△OCB∽△OFE,
∴
∴
∴FG=6,
∵正方形BGFE
∴GF=BE=6=EF,
∴
解之:OB=3
∴OE=OB+BE=3+6=9
∵点F在第一象限,
∴点F(9,6)
故答案为:A.
利用位似图形的性质,可证得△ODC∽△OGF,△OCB∽△OFE,利用相似三角形的性质可求出FG的长,同时可证得,利用正方形的性质可推出GF=BE=6=EF,代入计算求出OB的长,即可得到OE的长,可得到点F的坐标.
47.B
解:A、a3 a4=a7,故A不符合题意;
B、(a2)3=a6,故B符合题意;
C、a6÷a3=a3,故C不符合题意;
D、a3+a4,不能合并,故D不符合题意;
故答案为:B.
利用同底数幂相乘,底数不变,指数相加,可对A作出判断;利用幂的乘方法则,可对B作出判断;利用同底数幂相乘,底数不变,指数相减,可对C作出判断;只有同类项才能合并,可对D作出判断.
48.C
解:135亿=1.35×1010.
故答案为:C.
科学记数数法的表示形式为a×10n的形式。其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1(一亿=108),据此可得答案.
49.D
解:∵|-1|=1,|-2|=2,|-3|=3,
∴1<2<3,
∴,0>1>-2>-3,
∴最小的数是-3.
故答案为:D.
利用负数都小于0,几个负数比较大小,绝对值大的反而小,据此可得答案.
50.D
解:
但则明命题“若x2>1,则x>1”是假命题,
故答案为:D.
根据有理数的乘方计算法则以及假命题的概念即可求解.
专项1 单项选择2(浙江中考真题+中考模拟)
一、选择题
1.(2024·浙江)2024年浙江经济一季度GDP为201370000万元,其中201370000用科学记数法表示为( )
A. B.
C. D.
2.(2025·衢州模拟)计算:( )
A. B.3a C. D.3
3.(2024·浙江)有编号分别为的8个球,其中6个球一样重,另外两个都轻1克,为了找出这两个轻球,用天平称了三次:第一次比重,第二次比轻,第三次和一样重,则两个轻球的编号应该是( )
A.④⑤ B.③⑥ C.③⑤ D.③④
4.(2025·衢江模拟)(我国古代算题)马四匹,牛六头,共价四十八两(我国古代货币单位);马三匹,牛五头,共价三十八两.问马,牛各价几何?设马价为每匹两,牛价为每头两,则可列方程组为( )
A. B.
C. D.
5.(2025·鹿城模拟)小明在学习了勾股定理的证明后,尝试制作了四个全等三角形纸板,并拼出一个新图形,如图所示,若,则正方形的周长为( )
A.14 B.17 C.20 D.24
6.(2024·浙江)如图,在四边形中,,且,分别以四边形的四条边为边向形外作正方形、正方形、正方形、正方形,则图中各阴影部分面积和的最大值为( )
A.8 B.16 C.18 D.32
7.(2025·温州模拟)如图,数轴上点表示的数比点表示的数( )
A.大4 B.大2 C.小2 D.小4
8.(2025·衢州模拟)如图,在矩形ABCD中,点是对角线AC上一点,过点作分别交AD于F,BC于,连结BE,DE.记的面积为,则四边形BEDC的面积为( )
A. B.2s C. D.
9.(2025·衢州模拟)已知是一个正数,点都在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
10.(2025·衢州模拟)如图,是人字形钢架屋顶示意图(部分),其中,,且,则DF的长为( )
A. B. C. D.1
11.(2025·衢州模拟)若关于的一元二次方程有两个相等的实数根,则实数的值为( )
A.-16 B.-4 C.4 D.16
12.(2025·衢州模拟)因式分解:( )
A. B.
C. D.
13.(2025·衢州模拟)如图,在平面直角坐标系中,线段与线段AB是位似图形,位似中心为点.已知点的坐标分别为.若,则点的对应点的坐标是( )
A. B. C. D.
14.(2025·衢州模拟)某高速路段上的一台机动车雷达测速仪记录了一段时间内通过的九辆机动车速度,数据如下(单位:千米/时):100,96,86,77,96,93,108,96,95.这组数据的中位数是( )
A.96.5 B.96 C.95.5 D.94.5
15.(2025·衢州模拟)如图,点是正方形网格中的格点,点是以为圆心的圆与网格线的交点,直线经过点与点,则点关于直线的对称点是( )
A. B. C. D.
16.(2025·衢州模拟)下列四个数中,最小的数是( )
A.-2 B.-1 C.0 D.5
17.(2025·鹿城模拟)如图,在中,,设,,且是定值,点是上一点,点为中点,连接,将线段沿绕点顺时针旋转,得到线段交于点,若点关于直线的对称点恰为点,则下列线段长为定值的是( )
A. B. C. D.
18.(2025·鹿城模拟)一次空气污染指数抽查中,收集到一周的数据如下:70,70,63,82,91,91,75.该组数据的中位数是( )
A.63 B.82 C.91 D.75
19.(2025·鹿城模拟)如图是由个相同的小正方体组成的立体图形,它的主视图是( ).
A. B.
C. D.
20.(2025·钱塘模拟)复习课上,老师出了一道作图题:“如图,锐角内接于于点,点是的中点.仅用无刻度的直尺在上找出点,使.”课堂上同学们提供了以下两种方法.方法①:延长,交于点.方法②:作直线,,相交于点,连结,延长交于点.下列判断正确的是( )
A.方法①,方法②都错误 B.方法①,方法②都正确
C.方法①错误,方法②正确 D.方法①正确,方法②错误
21.(2025·钱塘模拟)如图,已知钟摆的摆长为米,当钟摆由位置摆动至位置时,钟摆摆动的角度为,此时摆幅的长可以表示为( )米
A. B. C. D.
22.(2025·钱塘模拟)如图,的切线交直径的延长线于点为切点.若的半径为2,则的长为( )
A. B.2 C. D.2
23.(2025·钱塘模拟)用五个相同的小立方体搭成以下几何体,其中主视图与其他3个不同的是( )
A. B.
C. D.
24.(2025·钱塘模拟)已知二次函数的图象开口向下,则的值可以是( )
A. B.0 C.2 D.4
25.(2025·衢江模拟)如图,在中,,连接对角线,点为中点,且,点是射线上一点,连接,作,交延长线于点.令,,则关于的函数表达式是( )
A. B. C. D.
26.(2025·衢江模拟)若,两点分别是双曲线和图象上的点.若,且,则和的大小为( )
A. B. C. D.
27.(2025·衢江模拟)如图,在直角坐标系中,的三个顶点分别为,,,现以原点为位似中心,在第一象限内作与的位似比为的位似图形,则点坐标为( )
A. B. C. D.
28.(2025·衢江模拟)下列式子的运算结果为的是( )
A. B. C. D.
29.(2025·衢江模拟)如图,已知两平行线、被直线所截,,则的度数为( )
A. B. C. D.
30.(2025·衢江模拟)下列各数中最大的数是( )
A.1 B.0 C. D.
31.(2025·镇海区模拟)已知二次函数的图象与轴没有交点,且,则( )
A. B. C. D.
32.(2025·镇海区模拟)已知矩形的顶点在半径为5的半圆上,顶点在直径上.若,则矩形的面积等于( )
A.22 B.23 C.24 D.25
33.(2025·镇海区模拟)在平面直角坐标系中,点一定位于( )
A.一次函数图象的上方 B.一次函数图象的下方
C.一次函数图象的上方 D.一次函数图象的下方
34.(2025·镇海区模拟)如图,在正方形中,将对角线绕点逆时针旋转角度,使得(为正实数).设.( )
A.若,则 B.若,则
C.若,则 D.若,则
35.(2025·镇海区模拟)已知一次函数的图象与反比例函数交于两点.当时,的面积为1,则当时,的面积为( )
A. B.1 C. D.2
36.(2025·镇海区模拟)如图,多边形是边长为1的正六边形,则( )
A. B. C. D.
37.(2025·镇海区模拟)我国“北斗导航系统”用的原子钟以纳秒级计算时间.已知1秒=1000000000纳秒,则数据1000000000用科学记数法可以表示为( )
A. B. C. D.
38.(2025·镇海区模拟)透过城市文旅LOGO可以窥见城市独有的文旅魅力.下列城市文旅LOGO是轴对称图形的是( )
A. B.
C. D.
39.(2025·金华模拟)下列运算中,不正确的是( )
A. B. C. D.
40.(2025·湖州模拟)中,,点,分别在边,上,连结,,,若,,,则的大小为( )
A. B. C. D.
41.(2025·湖州模拟)如图,在扇形中,,,过OB的中点C作交于点D,以C为圆心,的长为半径作弧交的延长线于点E,则图中阴影部分的面积为( )
A. B. C. D.
42.(2025·湖州模拟)与式子的值最接近的整数是( )
A.3 B.4 C.5 D.6
43.(2025·湖州模拟)计算结果为的是( )
A. B. C. D.
44.(2025·湖州模拟)按照国家统计局的数据,2024年中国生产芯片在4300亿颗以上,数据4300亿用科学记数法表示为( )
A. B. C. D.
45.(2025九下·东阳模拟)解不等式组:时,不等式①和不等式②的解集在数轴上表示正确的是( )
A. B.
C. D.
46.(2025九下·东阳模拟)如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以点O为位似中心的位似图形,且相似比为1:3,两个正方形在原点O同侧,点A、B、E在x轴上,其余顶点在第一象限,若正方形ABCD的边长为2,则点F的坐标( )
A.(9,6)
B.(3,2)
C.(6,9)
D.(2,3)
47.(2025九下·东阳模拟)下列运算正确的是( )
A.a3 a4=a12 B.(a2)3=a6 C.a6÷a3=a2 D.a3+a4=a7
48.(2025九下·东阳模拟)截止2025年2月23日15时26分。动画电影《哪吒之魔童闹海》累计票房(含预售)突破135亿,成为我国首部百亿电影!将数据“135亿”用科学记数法表示为( )
A.1.35×1011 B.13.5×1010 C.1.35×1010 D.1.35×109
49.(2025九下·东阳模拟)下列四个数中,最小的数是( )
A.0 B.-1 C.-2 D.-3
50.(2025九下·东阳模拟)下列选项中可以用来说明命题“若x2>1,则x>1”是假命题的反例是( )
A.x=1 B.x=-1 C.x=2 D.x=-2
答案解析部分
1.D
解:201370000=2.137×108.
故答案为:D.
根据科学记数法的表示形式为:a×10n,其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1
2.C
解:.
故答案为:C.
利用同分母分式相减法则计算.
3.A
4.D
解:由题意,可列方程组为:
;
故答案为:D.
根据题中的相等关系"四匹马的价格+六头牛的价格=四十八两,三匹马的价格+五头牛的价格=三十八两"列出关于x、y的方程组并结合各选项即可判断求解.
5.C
解:设每个三角形的长直角边为,短直角边为,
由题意可得,解得,
∴,
∴正方形的周长为,
故答案为:C.
设每个三角形的长直角边为,短直角边为,然后根据题意和图形可得关于a、b的方程组,解方程组求出的值,再根据勾股定理求得的长,最后根据正方形的周长边长计算即可求解.
6.B
7.D
解:
答案为:D.
数轴上右边的点表示的数字总比左边的点表示的数字大,其中大小差就是这两点之间的距离.
8.B
解:过点B作BM⊥AC于点M,过点D作DN⊥AC于点N,
∵四边形ABCD是矩形,
∴AB=CD,AB//CD,
∴∠BAM=∠DCN,
在△ABM与△CDN中,
,
∴△ABM≌△CDN(AAS),
∴BM=DN,
∵,
∴,
∴四边形BEDC的面积为2s.
故答案为:B.
先利用矩形的性质,证明△ABM≌△CDN,再根据全等三角形的性质,得出BM=DN,再利用三角形面积公式求解,从而求得四边形BEDC的面积.
9.A
解:∵ 点都在反比例函数的图象上,
∴
解得:
∵是一个正数,
∴
∴中最小,只有A符合.
故答案为:A.
先分别求得三个自变量的值,再根据a的符号来确定三个自变量的符号,然后利用排除法求解.
10.B
解:∵,,,
∴AE=BE=DE=4,
∵,
∴,
∴,解得:BF=.
又BE=DE,,
∴DF=BF=.
故答案为:B.
先根据直角三角形斜边上的中线的性质求得AE=BE=DE=4,再余弦求得BF,然后利用等腰三角形三线合一求得DF.
11.C
解:∵关于的一元二次方程有两个相等的实数根,
∴(-4)2-4m=0,解得:m=4.
故答案为:C.
根据一元二次方程有两个相等的实数根,列出关于m的方程求解.
12.D
解:.
故答案为:D.
利用平方差公式分解因式.
13.A
解:∵ 线段与线段AB是位似图形,位似中心为点 ,
∴OA':OA=OB':OB=A'B':AB,
∵ 点的坐标分别为,
∴A'B'=4-2=2.
又,
∴OA':OA=OB':OB=A'B':AB=2:3,
∴A的横坐标为2,纵坐标为3.
即A(3,).
故答案为:A.
先根据位似图形的性质,列出比例式,再求出A'B',结合AB=3求出位似比,再求出A点的坐标.
14.B
解:将数据从小到大排列为:77,86,93,95,96,96,96,100,108,所以中位数为.
故答案为:B.
先将数据从小到大排列,再求中位数.
15.D
解:∵PP4被直线m垂直平分,
∴关于直线的对称点是P4.
故答案为:D.
根据“关于一条直线对称的两个点的连线被这条直线垂直平分”求解.
16.A
解:将-2,-1,0,5从小到大排列为-2<-1<0<5,所以最小的数是-2.
故答案为:A.
先将四个数从小到大排列,再找出最小的数.
17.B
解:连接,,,在上取点H,使,连接,过点E作于点K,如图所示:
∵在中,,点为中点,
∴,
∴,
根据旋转可知:,,
∴和为等腰三角形,,
设,则,
∴,
∴,
根据轴对称可知:,,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,,
,
∴,
∴,
∴,
∴,
∴为的中位线,
∴,
∴、均不是定值,
∴,
∴为定值,
∵,,
∴,
∵,
∴,
∴,
∴,
∴为的中位线,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴不是定值,
综上分析可知,为定值.
故答案为:B.
连接,,,在上取点H,使,连接,过点E作于点K,根据直角三角形的性质得出,设,则,求出,得出,求出,得出,求出,,得出,求出,根据“平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例”可得比例式,结合比例式将AD=DK、ED用含x、y的代数式表示出来,由线段的和差将CD用含x、y的代数式表示出来,根据平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似可得△KEG∽△DFG,于是可得比例式,结合比例式可将DG用含x、y的代数式表示出来,由线段的和差将CG用含x、y的代数式表示出来即可求解.
18.D
解:将这组数据重新排序为:63,70,70,75,82, 91,91,
则其中位数为75,
故答案为:D.
中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数;根据中位数的定义并结合题意即可求解.
19.A
解:从正面看,底层是两个小正方形,第二层左边是一个小正方形,
故它的主视图是.
故答案为: .
根据主视图是从正面看得到的图形即可求解.
20.B
21.D
22.B
23.D
24.A
25.B
解:设交于点,过点作,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∵点为中点,
∴,,
∴,
∴,
∴,
∵,
∴,
∴,即:,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,即:,
∴;
故答案为:B.
设交于点,过点作,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的对应边的比相等可得比例式,同理可证,由相似三角形的对应边的比相等可得比例式,根据这个比例式可将BH用含x的代数式表示出来,根据“有两个角对应相等的两个三角形相似”可证,由相似三角形的对应边的比相等可得比例式,由比例式可得y与x之间的函数关系式.
26.A
解:将,两点分别代入和
得:,,
∴,,
∴,
∵,,
∴,
∴,
故答案为:A.
由题意,将,两点分别代入和可将x1、x2用含a、k1、k2的代数式表示出来,计算x1-x2的值,结合","即可判断符号,然后根据不等式的性质即可求解.
27.C
解:∵以原点为位似中心,在第一象限内作与的位似比为的位似图形,且点C的坐标为,
∴点坐标为,即:;
故答案为:C.
根据关于原点为位似中心的两个位似图形的对应点的坐标关系“横、纵坐标变为原来的2倍”计算即可求解.
28.D
解:A、∵,∴此选项不符合题意;
B、∵,∴此选项不符合题意;
C、∵,∴此选项不符合题意;
D、∵,∴此选项符合题意;
故答案为:D.
A、根据合并同类项法则“把同类项的系数相加,字母和字母的指数不变”可求解;
B、根据同底数幂的乘法法则“同底数幂相乘,底数不变,指数相加”可求解;
C、根据同底数幂的除法法则“同底数幂相除,底数不变,指数相减”可求解;
D、根据幂的乘方法则“幂的乘方,底数不变,指数相乘”可求解.
29.B
解:
∵,
∴,
∴;
故答案为:B.
根据平行线的性质“两直线平行,同位角相等”可得,再根据邻补角互补即可求解.
30.A
解:∵;
∴最大的数是1;
故答案为:A.
根据有理数大小的比较法则"负数小于0,0小于正数,两个负数,绝对值大的反而小"判断即可求解.
31.A
32.C
33.C
34.B
35.B
36.D
37.B
38.A
39.D
解:,故A正确;
,故B正确;
,故C正确;
,故D错误.
故答案为:D.
(1)利用合并同类项法则计算;
(2)利用同底数幂相乘法则计算;
(3)利用单项式除以单项式法则计算;
(4)利用幂的乘方法则计算.
40.D
41.D
42.B
43.C
44.C
45.C
解:由①得:x<2,
由②得:x≥-3,
∴此不等式组的解集为-3≤x<2,
此不等式组的解集在数轴上表示符合题意的是选项C.
故答案为:C.
分别求出不等式组中每一个不等式的解集,再确定出不等式组的解集,观察各选项,可得答案.
46.A
解:∵ 正方形ABCD与正方形BEFG是以点O为位似中心的位似图形,且相似比为1:3,
∴△ODC∽△OGF,△OCB∽△OFE,
∴
∴
∴FG=6,
∵正方形BGFE
∴GF=BE=6=EF,
∴
解之:OB=3
∴OE=OB+BE=3+6=9
∵点F在第一象限,
∴点F(9,6)
故答案为:A.
利用位似图形的性质,可证得△ODC∽△OGF,△OCB∽△OFE,利用相似三角形的性质可求出FG的长,同时可证得,利用正方形的性质可推出GF=BE=6=EF,代入计算求出OB的长,即可得到OE的长,可得到点F的坐标.
47.B
解:A、a3 a4=a7,故A不符合题意;
B、(a2)3=a6,故B符合题意;
C、a6÷a3=a3,故C不符合题意;
D、a3+a4,不能合并,故D不符合题意;
故答案为:B.
利用同底数幂相乘,底数不变,指数相加,可对A作出判断;利用幂的乘方法则,可对B作出判断;利用同底数幂相乘,底数不变,指数相减,可对C作出判断;只有同类项才能合并,可对D作出判断.
48.C
解:135亿=1.35×1010.
故答案为:C.
科学记数数法的表示形式为a×10n的形式。其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1(一亿=108),据此可得答案.
49.D
解:∵|-1|=1,|-2|=2,|-3|=3,
∴1<2<3,
∴,0>1>-2>-3,
∴最小的数是-3.
故答案为:D.
利用负数都小于0,几个负数比较大小,绝对值大的反而小,据此可得答案.
50.D
解:
但则明命题“若x2>1,则x>1”是假命题,
故答案为:D.
根据有理数的乘方计算法则以及假命题的概念即可求解.
同课章节目录
