专项1 单项选择3(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项1 单项选择3(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 692.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 13:17:06 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项1 单项选择3(浙江中考真题+中考模拟)
一、选择题
1.(2024·浙江)如图,正方形由四个全等的直角三角形(,,,)和中间一个小正方形组成,连接.若,,则( )
A.5 B. C. D.4
2.(2025·镇海区模拟)如图,在平面直角坐标系中,A、B两点在反比例函数 的图象上,延 长交x轴于C点,且,D是第二象限一点,且,若的面积是15, 则k的值为( )
A.8 B.10 C.11.5 D.13
3.(2024·金华真题)已知,则的值等于( )
A.10 B.-10 C.0 D.10或-10
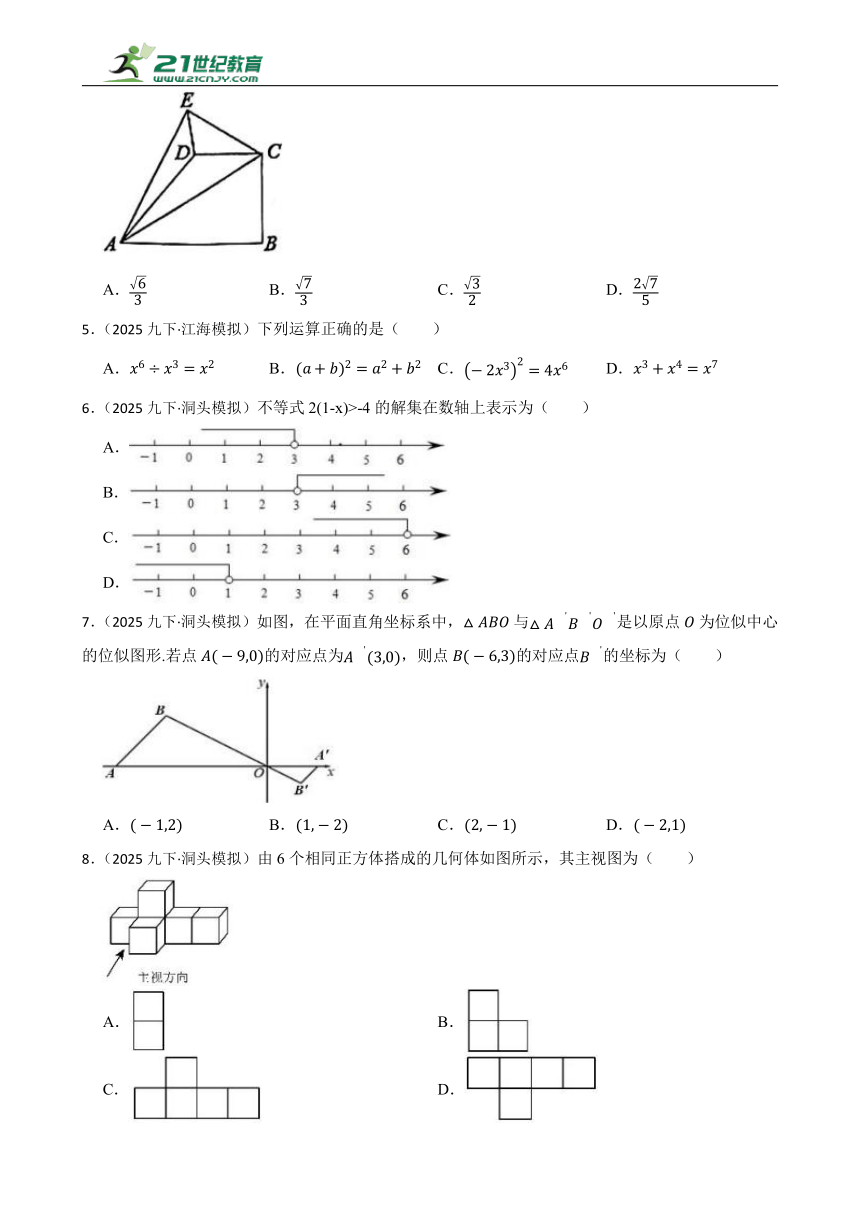
4.(2024·金华真题)如图,在四边形ABCD中,,把Rt沿着AC翻折得到Rt,若,则线段DE的长度( )
A. B. C. D.
5.(2025九下·江海模拟)下列运算正确的是( )
A. B. C. D.
6.(2025九下·洞头模拟)不等式2(1-x)>-4的解集在数轴上表示为( )
A.
B.
C.
D.
7.(2025九下·洞头模拟)如图,在平面直角坐标系中,与是以原点为位似中心的位似图形.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
8.(2025九下·洞头模拟)由6个相同正方体搭成的几何体如图所示,其主视图为( )
A. B.
C. D.
9.(2025九下·洞头模拟)下表记录了四个地区的最低海拔.
死海 吐鲁番 乌鲁木齐 青岛
-392米 -155米 918米 0米
以上四个地区海拔最低的地区是( )
A.死海 B.吐鲁番 C.乌鲁木齐 D.青岛
10.(2025·萧山模拟)如图,是的内接三角形,是的直径,若,,则图中阴影部分的面积为( )
A. B. C. D.
11.(2025·萧山模拟)实数2023的相反数是( )
A. B. C. D.2023
12.(2025·镇海区模拟)如图,已知内接于,点M为的中点,连接交于点E,且C为弧的中点,连接 ,在上存在点 H,使得 若 , 则的长( )
A.4 B. C. D.
13.(2025·镇海区模拟)在菱形中, 点E,F分别是, 的中点, 连接, .若 ,, 则的长为( )
A. B. C. D.6
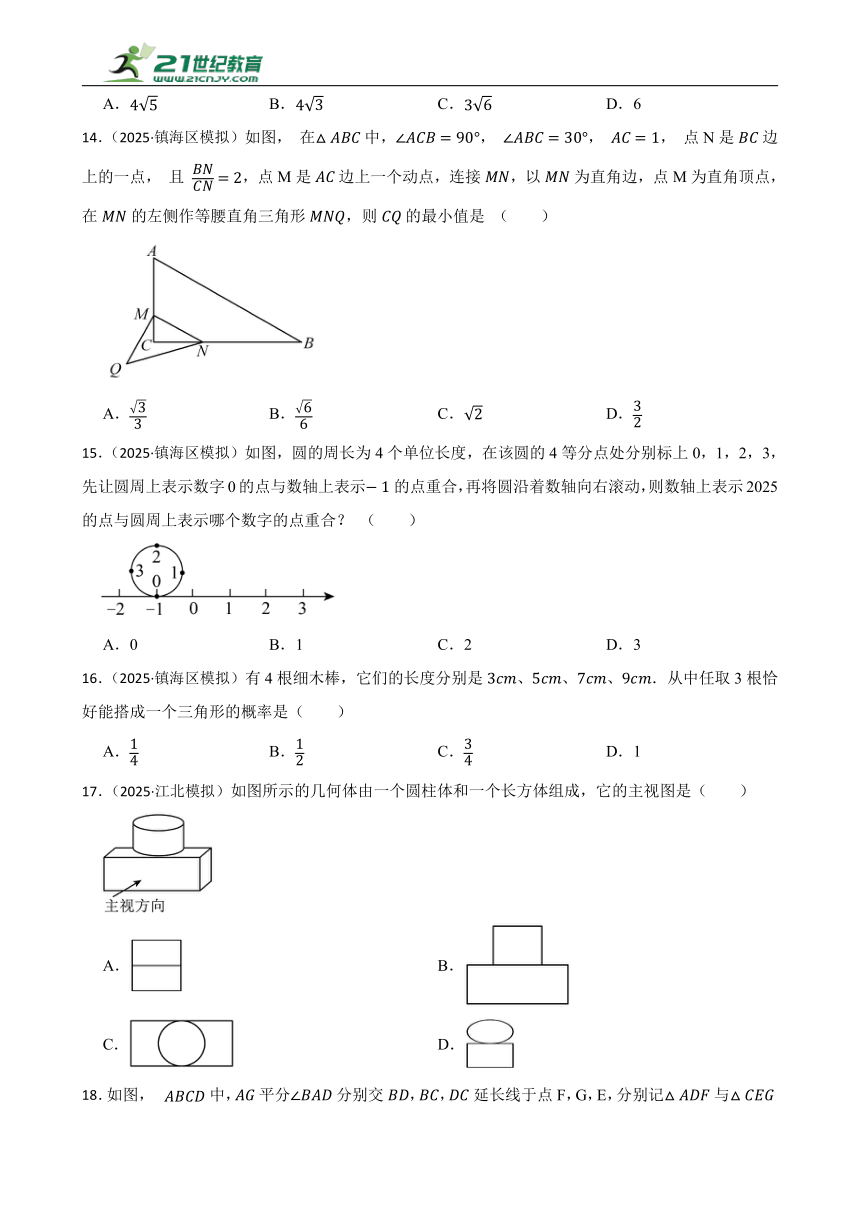
14.(2025·镇海区模拟)如图, 在中,, , , 点N是边上的一点, 且 ,点M是边上一个动点,连接,以为直角边,点M为直角顶点,在的左侧作等腰直角三角形,则的最小值是 ( )
A. B. C. D.
15.(2025·镇海区模拟)如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示的点重合,再将圆沿着数轴向右滚动,则数轴上表示2025的点与圆周上表示哪个数字的点重合? ( )
A.0 B.1 C.2 D.3
16.(2025·镇海区模拟)有4根细木棒,它们的长度分别是、、、.从中任取3根恰好能搭成一个三角形的概率是( )
A. B. C. D.1
17.(2025·江北模拟)如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )
A. B.
C. D.
18.如图,中,平分分别交,,延长线于点F,G,E,分别记与的面积为和.若,则的值是( )
A. B. C. D.
19.(2025·金华模拟)如图,在数轴上,点、分别表示、,且.若、两点之间的距离为6,则点表示的数为( )
A. B.0 C.3 D.
20.(2025·金华模拟)下列运算中,不正确的是( )
A. B. C. D.
21.(2025·金华模拟)下列说法中错误的是( )
A.两点之间线段最短
B.如果∠α=53°38',那么∠α余角的度数为36°22'
C.一个锐角的余角比这个角的补角小
D.互补的两个角一个是锐角一个是钝角
22.(2025·金华模拟)如图 所示为一个几何体的三视图, 那么这个几何体的侧面积是( )
A. B. C. D.
23.(2025九下·奉化模拟)若关于的一元二次方程有实数根,则字母的取值范围是( )
A.且 B. C. D.且
24.(2025九下·奉化模拟)下列计算正确的是( )
A. B.
C. D.
25.(2025九下·奉化模拟)2024年8月8日至11日期间,椒江葭沚老街举办了台州暑期消费季活动,四天的客流量超过58万人次,现场销售额高达4580000元,其中数据“4580000”用科学记数法表示为( )
A. B. C. D.
26.(2025九下·奉化模拟)如图,在正方形中,点在边上,是边上的中点,平分.若,则的长为( )
A. B. C. D.
27.(2025九下·奉化模拟)如图 29-9, 在边长为 1 的小正方形组成的网格中, 四个点均在格点上, 与 相交于点 , 连结 ,则 与 的周长比为 ( )
A. B. C. D.
28.(2025·鄞州模拟)在中,,a,b,c分别为的对边,且有,则的值为( )
A. B. C. D.
29.(2025·鄞州模拟)实数、在数轴上的位置如图所示,则下列说法正确的是( )
A. B. C. D.
30.(2025·鄞州模拟) 将点向下平移个单位长度后,再向左平移个单位长度的点为( )
A. B. C. D.
31.(2025·鄞州模拟)操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点纸片利用率100%.以上方案一、二的利用率分别为a、b,则( )
A. B. C. D.
32.(2025·鄞州模拟)下列说法正确的是
A.非零两数的和一定大于任何一个加数
B.非零两数的差一定小于被减数
C.大于1的两数之积一定大于任何一个因数
D.小于1的两数之商一定小于被除数
33.(2025·绍兴模拟)如图,正方形,分别取和边的中点、,连接、连接相交于点,连接,若,则的度数为( )
A. B. C. D.
34.(2025·绍兴模拟)下列说法:①一个数的绝对值一定是正数;②一个角的补角一定比这个角大;③若,则P是线段的中点;④多项式是三次四项式;⑤同角的余角相等.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
35.(2025·绍兴模拟)若,,则( )
A.或 B.或 C.或 D.或
36.(2025·绍兴模拟) 如图,分别以点A,B为圆心,大于AB 的长为半径作弧,交点分别为 M,N,连结MN交AC 于点D,下列说法一定正确的是( )
A.△ABD是直角三角形 B.△BCD是等腰三角形
C.△ABD是等腰三角形 D.△ABC是等腰三角形
37.(2025·绍兴模拟) 假期到了, 17 名女教师去外地培训, 住宿时有 2 人间和 3 人间可供租住, 每个房间都要住满, 她们的租住方案有( )
A.5 种 B.4 种 C.3 种 D.2 种
38.(2025九下·定海模拟)已知反比例函数 的图象与一次函数的图象交于点,.则下列各式的值最大的是( )
A. B. C. D.
39.(2025九下·定海模拟)下列各式在实数范围内不能分解因式的是( )
A. B. C. D.
40.(2025九下·定海模拟)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
41.(2025九下·定海模拟)下列两个数中,互为相反数的是( )
A.和 B.和 C.和 D.和
42.(2025九下·温州模拟)如图,在中,,设,且是定值.点是AC上一点,点为AB中点,连接CE,将线段CE绕点顺时针旋转,得到线段EF交AC于点,若点关于直线DE的对称点恰为点,则下列线段长为定值的是( )
A.AD B.CD C.CG D.DE
43.(2025·鹿城模拟)已知点在反比例函数的图象上,下列说法正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
44.(2025九下·温州模拟)小雯在学习了勾股定理的证明后,尝试制作了四个全等三角形纸板,并拼出一个新图形如图所示,若,则正方形ABCD的周长为( )
A.14 B.17 C.20 D.24
45.(2025九下·温州模拟)如图,在平面直角坐标系中,与是以点为位似中心的位似图形,若,,则点的坐标为( )
A. B. C. D.
46.(2025九下·温州模拟)不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
47.(2025九下·温州模拟)下列运算正确的是( )
A. B.
C. D.
48.(2025九下·温州模拟)如图是由5个相同的小正方体组成的立体图形,它的主视图是( )
A. B.
C. D.
49.(2025九下·温州模拟)下列四个数中,比-2小的数是( )
A.0 B.-1 C. D.-3
50.(2025九下·温州模拟)据统计我国每年浪费的粮食约35000000吨,我们要勤俭节约,反对浪费,积极的加入“光盘行动”中来.用科学记数法表示35000000是( ).
A.3.5×106 B.3.5×107 C.35×106 D.35×107
答案解析部分
1.C
解:∵ 正方形由四个全等的直角三角形(,,,)和中间一个小正方形组成,
∴AE=BF=DH=4,EF=HE,AH=BE=3,∠DHE=90°,
∴EF=BF-BE=4-3,
∴.
故答案为:C.
利用全等三角形的性质和正方形的性质可证得AE=BF=DH=4,EF=HE,AH=BE=3,∠DHE=90°,可求出EF的长,利用勾股定理求出DE的长.
2.B
3.D
4.B
解:如图,过点D作DM⊥CE,
由折叠可知:∠AEC=∠B=90°,
∴AE//DM,
∴∠AED=∠EDM,
∴,
∵∠ACB=60°,∠ECD=30°,
设,由折叠性质可知,,
∴,
由翻折可知:∠ECA=∠BCA=60°,
∴∠ECD=30°,
∴,
∴,
∴,
即,
解得:,
∴,,
在直角三角形EDM中,DE2=DM2+EM2,
解得:,
故答案为:B.
过点D作DM⊥CE,首先得到∠ACB=60度,∠ECD=30度,再根据折叠可得到∠AED=∠EDM,设,由折叠性质可知,EC=CB,在直角三角形EDM中,根据勾股定理即可得DE的长.
5.C
6.A
解:解不等式,
可得,
将解集在数轴上表示出来,如下图所示:
故答案为:A.
本题考查解一元一次不等式以及在数轴上表示不等式的解集.先去括号解不等式可得:,在将解集在数轴上表示出来可选出答案.
7.C
解:∵,,
∴,
∴,
∵与是以原点为位似中心的位似图形,
∴与的相似比为3,
又∵,
∴.
故答案为:C.
本题考查位似图形.已知点、点的坐标,可得,据此可求出,进而可得与的相似比为3,再根据,利用位似的性质可求出对应点的坐标.
8.C
解:几何体的主视图是:
故答案为:C.
本题考查组合体的三视图.根据主视图的定义,主视图是从正面看到的图形,进而可选出答案.
9.A
解:∵,
∴海拔最低的地区是死海.
故答案为:A.
本题考查有理数大小比较的实际应用.根据负数小于零、正数大于零,先将四个数进行比较可得:,据此可找出四个地区海拔最低的地区.
10.C
11.A
12.C
13.A
14.B
15.C
16.C
17.B
解:从正面看下面是一个比较长的矩形,上面是一个比较窄的矩形.
故答案为:B.
根据主视图的定义"主视图是从前面看所得到的图形"并结合几何体和各选项即可求解.
18.A
19.A
解:
∴a、b互为相反数,
∵A、B两点间的距离为6,
∴点A、B分别在距离原点3的位置上,
∴点A表示的数为
故答案为:C.
根据 A、B两点间的距离为6判断出点A、B分别表示的数即可.
20.C
解:A: 故A正确;
B: 故B正确;
C: 故C错误;
D: 故D正确.
故答案为:C.
根据合并同类项、同底数幂的乘法、幂的乘方以及同底数幂的除法法则逐项判断解题.
21.D
解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38',那么∠α余角的度数为90°-53°38'= 36°22',故本小题正确,不符合题意;
C、一个锐角α的余角是90°-α,这个角的补角是180°- x,(180°-α)-(90°-α)= 90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故答案为:D.
根据线段的性质,余角与补角的定义对各小题分析判断后利用排除法求解.
22.B
解:根据题意,圆锥的底面半径r为:6÷2=3.
母线l=,
则由圆锥的侧面积公式得S=πrl=π 5 3=15π.
故答案为:B.
根据几何体的主视图和左视图都是等腰三角形,俯视图是圆,判断出该几何体是圆锥.再根据圆锥的侧面积公式解答即可.
23.D
解:∵关于x的一元二次方程 有实数根,
且
解得: 且
故答案为:D.
利用一元二次方程的定义和根的判别式的意义即可求解.
24.D
解:与 不是同类项,不能合并,故本选项错误;
故本选项错误;
故本选项错误;
故本选项正确.
故答案为:D.
根据合并同类项、幂的乘方、同底数幂的除法、单项式乘以单项式的运算法则逐一判断解题.
25.A
解:4580000用科学记数法表示为.
故答案为:A.
科学记数法一般形式为,其中,n是小数点向左移动的位数.
26.C
解:如图,延长,相交于点,
∵正方形,,
∴,,
∴,
∴,,
∵是边上的中点,
∴,
∴,
∴,
∵平分,
∴,
∴,
∴,
设,则,,
在中,,
∴,
解得,
∴,
故答案为:.
延长,相交于点,即可得到,求出,利用平行线和角平分线得到,即可得到,设,在中根据勾股定理求出的值解题即可.
27.D
解:设AB过格点M,如图忾示,
观察图形可得,,,
∴,
而,
∴四边形为平行四边形,
∴,
∴,,
∴,
∴.
故答案为:D.
先证明四边形为平行四边形,再证明,利相似三角形周长的比等于相似比即可求出.
28.D
解:
如图所示:
得到
故答案为:D.
首先根据题意画出图形,然后利用 得到 ,然后利用勾股定理求出 然后利用正弦的概念求解即可.
29.B
解:观察数轴可知:
此 选项的计算错误,故此选项不符合题意;
此选项的计算正确,故此选项符合题意;
此 选项的计算错误,故此选项不符合题意;
∴此选项的判断错误,故此选项不符合题意;
故答案为:B.
先观察数轴判断a,b的大小和绝对值的大小,从而判断D选项的正误;根据有理数的加法法则判断 的大小,从而判断A选项的正误;根据有理数的减法法则判断 大小,从而判断B选项的正误;根据有理数的乘法法则判断 ab的大小,从而判断C选项的正误.
30.A
解:将点A(3,2)向下平移2个单位长度后,再向左平移4个单位长度的点为(
即
故答案为:A.
根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算即可.
31.D
解:方案一中,连接,,,
,
∵棱长为1cm的正方体纸盒,
∴,,
∴,即,
∴为该圆的直径,
∴该圆的半径为:,
∴,
方案二中先将图进行命名:
,
∵,,
∴,
∴,即,
∴,即,
∵,
∴,
∴,即,
∴,
∴,
∵,
∴,
故答案为:D.
连接,,,根据勾股定理的逆定理可得,即可得到为该圆的直径,利用勾股定理即可求出,方案二中得到,,然后根据相似三角形的对应边成比例解题即可.
32.C
解: 两个负数的和小于任何一个加数,
选项 不符合题意;
当减数是小于或等于0的数时,差是大于或等于被减数的,
选项 不符合题意;
大于1的两数之积一定大于任何一个因数,
选项 符合题意;
当除数是真分数,被除数是正数时,商大于被除数,
选项 不符合题意.
故答案为:C.
根据有理数的加法法则可判断A;根据有理数的减法法则可判断B;根据有理数的乘法法则可判断C;根据有理数的除法法则可判断D.
33.D
解:延长AF交BC的延长线于H,如图所示:
∵四边形ABCD是正方形,
∥BC,
∵点E, F分别是AD, BC的中点,
在 和 中,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠1=α.
∵∠1+∠2 =∠BAD = 90°,
∴∠ABE+∠2=90°,
∴∠BGA=90°
∴∠BGH=90°,
∵AD∥BC,
∴∠1=∠H =α,
在△ADF和△HCF中,
∴△ADF≌△HCF(AAS),
∴AD=CH=BC,
即点D是Rt△BCH斜边上的中点,
∴CG=BC=CH,
∴∠CGH=∠H=α,
∴∠BCG =∠CGH+∠H = 2α,
∴∠DCG=90°-∠BCG=90°--2α.
故答案为:D.
延长AF交BC的延长线于H,先证明△ABE和△DAF全等得∠ABE=∠1=α, 进而得∠BGA=∠BGH =90°, 再证明△ADF和△HCF全等得AD =CH = BC, 由此可得CG=BC=CH, 则∠CGH=∠H=α, 进而得∠BCG=2α, 由此即可得出答案.
34.A
解:①一个数的绝对值一定是正数或0,故①错误;
②一个角的补角不一定比这个角大,如钝角的补角是锐角,故②错误;
③若 ,且P在线段AB上,则P是线段AB的中点,故③错误;
④多项式: 是三次四项式,正确;
⑤同角的余角相等,正确.
故答案为:A.
根据绝对值的性质,余角和补角,线段中点的定义,多项式的定义,逐一判断即可解答.
35.D
解:
或
解得: 或
当 时,
当 时,
综上, 的值为5或3,
故答案为:D.
根据绝对值的性质求出a,再将a、b的值代入计算即可.
36.C
解:由作图过程可得MN是AB的垂直平分线,
∴AD=BD,
∴△ABD是等腰三角形.
故答案为:C.
由作图过程可得MN是AB的垂直平分线,由线段垂直平分线上的点到线段两端点的距离相等得AD=BD,进而根据两边相等的三角形就是等腰三角形即可判断得出答案.
37.C
解:设住3人间的需要有x间,住2人间的需要有y间,
根据题意可得:3x+2y=17,
∵2y是偶数,17是奇数,
∴3x只能是奇数,即x必须是奇数,
当x=1时,y=7,
当x=3时,y=4,
当x=5时,y=1,
综合以上得知,第一种是:1间住3人的,7间住2人的,
第二种是:3间住3人的,4间住2人的,
第三种是:5间住3人的,1间住2人的,
∴有3种不同的安排.
故答案为:C.
设住3人间的需要有x间,住2人间的需要有y间,根据“17 名女教师去外地培训”列出方程3x+2y=17,再求解即可.
38.B
解:∵反比例函数 的象与一次函数 的象交于点.
∴反比例函数象分布在第一、三象限,点A、B不在同一象限内, 当点A在第三象限,点B在第一象限,且
故答案为:B.
根据反比例函数和一次函数的图象可知交点分别位于分别一、三象限,然后根据增减性逐一判断解题.
39.C
解:A、令 则 所以在实数范围内能分解因式;
B、令 则 所以在实数范围内能分解因式;
C、令 则 所以 在实数范围内不能分解因式;
D、令 则 当 时, 所以 在实数范围内能分解因式.
故答案为:C.
根据二次多项式在实数范围内可以分解因式当且仅当其判别式 Δ=b2 4ac大于或等于0逐项判断解题.
40.B
解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、不是轴对称图形,也不是中心对称图形,故本选项错误;
C、是轴对称图形,不是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
根据轴对称图形与中心对称图形的概念“ 轴对称图形是指一个图形沿一条直线折叠,直线两旁的部分能够互相重合;而中心对称图形是指一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合 ”对各选项分析判断后利用排除法求解.
41.D
解:故 和 不互为相反数,原选项不符合题意;
故 和|4|不互为相反数,原选项不符合题意;
和 不互为相反数,原选项不符合题意;
故 和 互为相反数,原选项符合题意;
故答案为:D.
根据相反数的定义和化简绝对值逐项排除即可.
42.B
解:如图所示,连接.
中,
为的中点
中,
关于直线对称
设,则
中,,即:
整理得:,即:
是定值,
为定值.
故答案为:B.
由于轴对称图形的对应角相等,结合旋转的定义可推导出是直角,则是和的公共斜边,由直角三角形斜边上的中线等于斜边的一半及勾股定理可表示出的平方值,进而可表示出的平方值,此时可设出的长,则可分别表示出的长,利用勾股定理可得出,由于只知道是定值,即都是变量,所以线段的值不固定,但由于则可继续表示出的值,此时恰好得出的值是的一半,则只有是定值.
43.C
解:反比例函数
异号,即双曲线的两个分支分别在第二、四象限
(1)当时
当时,
当且时,
(2)当时
当时,
当且时,
综上所述:
A、若,则或,结果错误;
B、若,则或,结果错误;
C、若,则,即结果正确;
D、若,则,结果错误;
故答案为:C.
由于反比例系数,所以与符号相反,当时,与异号,则必然有与异号,即,故选项C正确;当时,应分类讨论,若两点都在第二象限,则与同号,此时;若两点分别在第二和第四象限,则与异号,此时;反之亦然,故选项都错误;当时,则与同号,则两点在同一象限,即与也同号,则,故选项D错误。
44.C
解:由题意知:
设,则
解得:
正方形ABCD的周长为
故答案为:C.
求正方形的周长,实质是求边长的值;由于图中四个直角三角形全等,则实质告诉了中两直角边与的和与差,则容易求得与的值,再利用勾股定理即可求出的值。
45.A
解:
,即点为中点
,即
故答案为:A.
由于位似图形是相似图形,且其中一组对应边可知,则利用相似比可确定点为中点,又点坐标已知,可借助中点公式直接求出点的坐标。
46.B
47.C
解:A、,结果错误;
B、,结果错误;
C、,结果正确;
D、,结果错误;
故答案为:C.
整式运算中首先要牢记合并同类项法则,即字母与字母的指数都不变,只把系数加减;其次要熟练使用幂的一些运算,如:
48.A
解:A、主视图,正确;
B、是从物体后面观察到的视图,不符合题意;
C、无论从哪个方向观察也得不到这个视图,不符合题意;
D、是左视图,不符合题意
故答案为:A.
主视图是指从物体正面观察得到的视图,左视图是指从物体从左边观察得到的视图,主视图是指从物体上面观察得到的视图.
49.D
解:
故答案为:D.
负数比较大小,绝对值大的反而小。
50.B
解:用科学记数法表示35000000是:3.5×107
故答案为:B.
科学记数法表示一个绝对值大于或等于1的数可以写成a×10n的形式,其中1≤<10,n等于原数的整数位数减1,据此即可解决问题.
专项1 单项选择3(浙江中考真题+中考模拟)
一、选择题
1.(2024·浙江)如图,正方形由四个全等的直角三角形(,,,)和中间一个小正方形组成,连接.若,,则( )
A.5 B. C. D.4
2.(2025·镇海区模拟)如图,在平面直角坐标系中,A、B两点在反比例函数 的图象上,延 长交x轴于C点,且,D是第二象限一点,且,若的面积是15, 则k的值为( )
A.8 B.10 C.11.5 D.13
3.(2024·金华真题)已知,则的值等于( )
A.10 B.-10 C.0 D.10或-10
4.(2024·金华真题)如图,在四边形ABCD中,,把Rt沿着AC翻折得到Rt,若,则线段DE的长度( )
A. B. C. D.
5.(2025九下·江海模拟)下列运算正确的是( )
A. B. C. D.
6.(2025九下·洞头模拟)不等式2(1-x)>-4的解集在数轴上表示为( )
A.
B.
C.
D.
7.(2025九下·洞头模拟)如图,在平面直角坐标系中,与是以原点为位似中心的位似图形.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
8.(2025九下·洞头模拟)由6个相同正方体搭成的几何体如图所示,其主视图为( )
A. B.
C. D.
9.(2025九下·洞头模拟)下表记录了四个地区的最低海拔.
死海 吐鲁番 乌鲁木齐 青岛
-392米 -155米 918米 0米
以上四个地区海拔最低的地区是( )
A.死海 B.吐鲁番 C.乌鲁木齐 D.青岛
10.(2025·萧山模拟)如图,是的内接三角形,是的直径,若,,则图中阴影部分的面积为( )
A. B. C. D.
11.(2025·萧山模拟)实数2023的相反数是( )
A. B. C. D.2023
12.(2025·镇海区模拟)如图,已知内接于,点M为的中点,连接交于点E,且C为弧的中点,连接 ,在上存在点 H,使得 若 , 则的长( )
A.4 B. C. D.
13.(2025·镇海区模拟)在菱形中, 点E,F分别是, 的中点, 连接, .若 ,, 则的长为( )
A. B. C. D.6
14.(2025·镇海区模拟)如图, 在中,, , , 点N是边上的一点, 且 ,点M是边上一个动点,连接,以为直角边,点M为直角顶点,在的左侧作等腰直角三角形,则的最小值是 ( )
A. B. C. D.
15.(2025·镇海区模拟)如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示的点重合,再将圆沿着数轴向右滚动,则数轴上表示2025的点与圆周上表示哪个数字的点重合? ( )
A.0 B.1 C.2 D.3
16.(2025·镇海区模拟)有4根细木棒,它们的长度分别是、、、.从中任取3根恰好能搭成一个三角形的概率是( )
A. B. C. D.1
17.(2025·江北模拟)如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )
A. B.
C. D.
18.如图,中,平分分别交,,延长线于点F,G,E,分别记与的面积为和.若,则的值是( )
A. B. C. D.
19.(2025·金华模拟)如图,在数轴上,点、分别表示、,且.若、两点之间的距离为6,则点表示的数为( )
A. B.0 C.3 D.
20.(2025·金华模拟)下列运算中,不正确的是( )
A. B. C. D.
21.(2025·金华模拟)下列说法中错误的是( )
A.两点之间线段最短
B.如果∠α=53°38',那么∠α余角的度数为36°22'
C.一个锐角的余角比这个角的补角小
D.互补的两个角一个是锐角一个是钝角
22.(2025·金华模拟)如图 所示为一个几何体的三视图, 那么这个几何体的侧面积是( )
A. B. C. D.
23.(2025九下·奉化模拟)若关于的一元二次方程有实数根,则字母的取值范围是( )
A.且 B. C. D.且
24.(2025九下·奉化模拟)下列计算正确的是( )
A. B.
C. D.
25.(2025九下·奉化模拟)2024年8月8日至11日期间,椒江葭沚老街举办了台州暑期消费季活动,四天的客流量超过58万人次,现场销售额高达4580000元,其中数据“4580000”用科学记数法表示为( )
A. B. C. D.
26.(2025九下·奉化模拟)如图,在正方形中,点在边上,是边上的中点,平分.若,则的长为( )
A. B. C. D.
27.(2025九下·奉化模拟)如图 29-9, 在边长为 1 的小正方形组成的网格中, 四个点均在格点上, 与 相交于点 , 连结 ,则 与 的周长比为 ( )
A. B. C. D.
28.(2025·鄞州模拟)在中,,a,b,c分别为的对边,且有,则的值为( )
A. B. C. D.
29.(2025·鄞州模拟)实数、在数轴上的位置如图所示,则下列说法正确的是( )
A. B. C. D.
30.(2025·鄞州模拟) 将点向下平移个单位长度后,再向左平移个单位长度的点为( )
A. B. C. D.
31.(2025·鄞州模拟)操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点纸片利用率100%.以上方案一、二的利用率分别为a、b,则( )
A. B. C. D.
32.(2025·鄞州模拟)下列说法正确的是
A.非零两数的和一定大于任何一个加数
B.非零两数的差一定小于被减数
C.大于1的两数之积一定大于任何一个因数
D.小于1的两数之商一定小于被除数
33.(2025·绍兴模拟)如图,正方形,分别取和边的中点、,连接、连接相交于点,连接,若,则的度数为( )
A. B. C. D.
34.(2025·绍兴模拟)下列说法:①一个数的绝对值一定是正数;②一个角的补角一定比这个角大;③若,则P是线段的中点;④多项式是三次四项式;⑤同角的余角相等.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
35.(2025·绍兴模拟)若,,则( )
A.或 B.或 C.或 D.或
36.(2025·绍兴模拟) 如图,分别以点A,B为圆心,大于AB 的长为半径作弧,交点分别为 M,N,连结MN交AC 于点D,下列说法一定正确的是( )
A.△ABD是直角三角形 B.△BCD是等腰三角形
C.△ABD是等腰三角形 D.△ABC是等腰三角形
37.(2025·绍兴模拟) 假期到了, 17 名女教师去外地培训, 住宿时有 2 人间和 3 人间可供租住, 每个房间都要住满, 她们的租住方案有( )
A.5 种 B.4 种 C.3 种 D.2 种
38.(2025九下·定海模拟)已知反比例函数 的图象与一次函数的图象交于点,.则下列各式的值最大的是( )
A. B. C. D.
39.(2025九下·定海模拟)下列各式在实数范围内不能分解因式的是( )
A. B. C. D.
40.(2025九下·定海模拟)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
41.(2025九下·定海模拟)下列两个数中,互为相反数的是( )
A.和 B.和 C.和 D.和
42.(2025九下·温州模拟)如图,在中,,设,且是定值.点是AC上一点,点为AB中点,连接CE,将线段CE绕点顺时针旋转,得到线段EF交AC于点,若点关于直线DE的对称点恰为点,则下列线段长为定值的是( )
A.AD B.CD C.CG D.DE
43.(2025·鹿城模拟)已知点在反比例函数的图象上,下列说法正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
44.(2025九下·温州模拟)小雯在学习了勾股定理的证明后,尝试制作了四个全等三角形纸板,并拼出一个新图形如图所示,若,则正方形ABCD的周长为( )
A.14 B.17 C.20 D.24
45.(2025九下·温州模拟)如图,在平面直角坐标系中,与是以点为位似中心的位似图形,若,,则点的坐标为( )
A. B. C. D.
46.(2025九下·温州模拟)不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
47.(2025九下·温州模拟)下列运算正确的是( )
A. B.
C. D.
48.(2025九下·温州模拟)如图是由5个相同的小正方体组成的立体图形,它的主视图是( )
A. B.
C. D.
49.(2025九下·温州模拟)下列四个数中,比-2小的数是( )
A.0 B.-1 C. D.-3
50.(2025九下·温州模拟)据统计我国每年浪费的粮食约35000000吨,我们要勤俭节约,反对浪费,积极的加入“光盘行动”中来.用科学记数法表示35000000是( ).
A.3.5×106 B.3.5×107 C.35×106 D.35×107
答案解析部分
1.C
解:∵ 正方形由四个全等的直角三角形(,,,)和中间一个小正方形组成,
∴AE=BF=DH=4,EF=HE,AH=BE=3,∠DHE=90°,
∴EF=BF-BE=4-3,
∴.
故答案为:C.
利用全等三角形的性质和正方形的性质可证得AE=BF=DH=4,EF=HE,AH=BE=3,∠DHE=90°,可求出EF的长,利用勾股定理求出DE的长.
2.B
3.D
4.B
解:如图,过点D作DM⊥CE,
由折叠可知:∠AEC=∠B=90°,
∴AE//DM,
∴∠AED=∠EDM,
∴,
∵∠ACB=60°,∠ECD=30°,
设,由折叠性质可知,,
∴,
由翻折可知:∠ECA=∠BCA=60°,
∴∠ECD=30°,
∴,
∴,
∴,
即,
解得:,
∴,,
在直角三角形EDM中,DE2=DM2+EM2,
解得:,
故答案为:B.
过点D作DM⊥CE,首先得到∠ACB=60度,∠ECD=30度,再根据折叠可得到∠AED=∠EDM,设,由折叠性质可知,EC=CB,在直角三角形EDM中,根据勾股定理即可得DE的长.
5.C
6.A
解:解不等式,
可得,
将解集在数轴上表示出来,如下图所示:
故答案为:A.
本题考查解一元一次不等式以及在数轴上表示不等式的解集.先去括号解不等式可得:,在将解集在数轴上表示出来可选出答案.
7.C
解:∵,,
∴,
∴,
∵与是以原点为位似中心的位似图形,
∴与的相似比为3,
又∵,
∴.
故答案为:C.
本题考查位似图形.已知点、点的坐标,可得,据此可求出,进而可得与的相似比为3,再根据,利用位似的性质可求出对应点的坐标.
8.C
解:几何体的主视图是:
故答案为:C.
本题考查组合体的三视图.根据主视图的定义,主视图是从正面看到的图形,进而可选出答案.
9.A
解:∵,
∴海拔最低的地区是死海.
故答案为:A.
本题考查有理数大小比较的实际应用.根据负数小于零、正数大于零,先将四个数进行比较可得:,据此可找出四个地区海拔最低的地区.
10.C
11.A
12.C
13.A
14.B
15.C
16.C
17.B
解:从正面看下面是一个比较长的矩形,上面是一个比较窄的矩形.
故答案为:B.
根据主视图的定义"主视图是从前面看所得到的图形"并结合几何体和各选项即可求解.
18.A
19.A
解:
∴a、b互为相反数,
∵A、B两点间的距离为6,
∴点A、B分别在距离原点3的位置上,
∴点A表示的数为
故答案为:C.
根据 A、B两点间的距离为6判断出点A、B分别表示的数即可.
20.C
解:A: 故A正确;
B: 故B正确;
C: 故C错误;
D: 故D正确.
故答案为:C.
根据合并同类项、同底数幂的乘法、幂的乘方以及同底数幂的除法法则逐项判断解题.
21.D
解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38',那么∠α余角的度数为90°-53°38'= 36°22',故本小题正确,不符合题意;
C、一个锐角α的余角是90°-α,这个角的补角是180°- x,(180°-α)-(90°-α)= 90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故答案为:D.
根据线段的性质,余角与补角的定义对各小题分析判断后利用排除法求解.
22.B
解:根据题意,圆锥的底面半径r为:6÷2=3.
母线l=,
则由圆锥的侧面积公式得S=πrl=π 5 3=15π.
故答案为:B.
根据几何体的主视图和左视图都是等腰三角形,俯视图是圆,判断出该几何体是圆锥.再根据圆锥的侧面积公式解答即可.
23.D
解:∵关于x的一元二次方程 有实数根,
且
解得: 且
故答案为:D.
利用一元二次方程的定义和根的判别式的意义即可求解.
24.D
解:与 不是同类项,不能合并,故本选项错误;
故本选项错误;
故本选项错误;
故本选项正确.
故答案为:D.
根据合并同类项、幂的乘方、同底数幂的除法、单项式乘以单项式的运算法则逐一判断解题.
25.A
解:4580000用科学记数法表示为.
故答案为:A.
科学记数法一般形式为,其中,n是小数点向左移动的位数.
26.C
解:如图,延长,相交于点,
∵正方形,,
∴,,
∴,
∴,,
∵是边上的中点,
∴,
∴,
∴,
∵平分,
∴,
∴,
∴,
设,则,,
在中,,
∴,
解得,
∴,
故答案为:.
延长,相交于点,即可得到,求出,利用平行线和角平分线得到,即可得到,设,在中根据勾股定理求出的值解题即可.
27.D
解:设AB过格点M,如图忾示,
观察图形可得,,,
∴,
而,
∴四边形为平行四边形,
∴,
∴,,
∴,
∴.
故答案为:D.
先证明四边形为平行四边形,再证明,利相似三角形周长的比等于相似比即可求出.
28.D
解:
如图所示:
得到
故答案为:D.
首先根据题意画出图形,然后利用 得到 ,然后利用勾股定理求出 然后利用正弦的概念求解即可.
29.B
解:观察数轴可知:
此 选项的计算错误,故此选项不符合题意;
此选项的计算正确,故此选项符合题意;
此 选项的计算错误,故此选项不符合题意;
∴此选项的判断错误,故此选项不符合题意;
故答案为:B.
先观察数轴判断a,b的大小和绝对值的大小,从而判断D选项的正误;根据有理数的加法法则判断 的大小,从而判断A选项的正误;根据有理数的减法法则判断 大小,从而判断B选项的正误;根据有理数的乘法法则判断 ab的大小,从而判断C选项的正误.
30.A
解:将点A(3,2)向下平移2个单位长度后,再向左平移4个单位长度的点为(
即
故答案为:A.
根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算即可.
31.D
解:方案一中,连接,,,
,
∵棱长为1cm的正方体纸盒,
∴,,
∴,即,
∴为该圆的直径,
∴该圆的半径为:,
∴,
方案二中先将图进行命名:
,
∵,,
∴,
∴,即,
∴,即,
∵,
∴,
∴,即,
∴,
∴,
∵,
∴,
故答案为:D.
连接,,,根据勾股定理的逆定理可得,即可得到为该圆的直径,利用勾股定理即可求出,方案二中得到,,然后根据相似三角形的对应边成比例解题即可.
32.C
解: 两个负数的和小于任何一个加数,
选项 不符合题意;
当减数是小于或等于0的数时,差是大于或等于被减数的,
选项 不符合题意;
大于1的两数之积一定大于任何一个因数,
选项 符合题意;
当除数是真分数,被除数是正数时,商大于被除数,
选项 不符合题意.
故答案为:C.
根据有理数的加法法则可判断A;根据有理数的减法法则可判断B;根据有理数的乘法法则可判断C;根据有理数的除法法则可判断D.
33.D
解:延长AF交BC的延长线于H,如图所示:
∵四边形ABCD是正方形,
∥BC,
∵点E, F分别是AD, BC的中点,
在 和 中,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠1=α.
∵∠1+∠2 =∠BAD = 90°,
∴∠ABE+∠2=90°,
∴∠BGA=90°
∴∠BGH=90°,
∵AD∥BC,
∴∠1=∠H =α,
在△ADF和△HCF中,
∴△ADF≌△HCF(AAS),
∴AD=CH=BC,
即点D是Rt△BCH斜边上的中点,
∴CG=BC=CH,
∴∠CGH=∠H=α,
∴∠BCG =∠CGH+∠H = 2α,
∴∠DCG=90°-∠BCG=90°--2α.
故答案为:D.
延长AF交BC的延长线于H,先证明△ABE和△DAF全等得∠ABE=∠1=α, 进而得∠BGA=∠BGH =90°, 再证明△ADF和△HCF全等得AD =CH = BC, 由此可得CG=BC=CH, 则∠CGH=∠H=α, 进而得∠BCG=2α, 由此即可得出答案.
34.A
解:①一个数的绝对值一定是正数或0,故①错误;
②一个角的补角不一定比这个角大,如钝角的补角是锐角,故②错误;
③若 ,且P在线段AB上,则P是线段AB的中点,故③错误;
④多项式: 是三次四项式,正确;
⑤同角的余角相等,正确.
故答案为:A.
根据绝对值的性质,余角和补角,线段中点的定义,多项式的定义,逐一判断即可解答.
35.D
解:
或
解得: 或
当 时,
当 时,
综上, 的值为5或3,
故答案为:D.
根据绝对值的性质求出a,再将a、b的值代入计算即可.
36.C
解:由作图过程可得MN是AB的垂直平分线,
∴AD=BD,
∴△ABD是等腰三角形.
故答案为:C.
由作图过程可得MN是AB的垂直平分线,由线段垂直平分线上的点到线段两端点的距离相等得AD=BD,进而根据两边相等的三角形就是等腰三角形即可判断得出答案.
37.C
解:设住3人间的需要有x间,住2人间的需要有y间,
根据题意可得:3x+2y=17,
∵2y是偶数,17是奇数,
∴3x只能是奇数,即x必须是奇数,
当x=1时,y=7,
当x=3时,y=4,
当x=5时,y=1,
综合以上得知,第一种是:1间住3人的,7间住2人的,
第二种是:3间住3人的,4间住2人的,
第三种是:5间住3人的,1间住2人的,
∴有3种不同的安排.
故答案为:C.
设住3人间的需要有x间,住2人间的需要有y间,根据“17 名女教师去外地培训”列出方程3x+2y=17,再求解即可.
38.B
解:∵反比例函数 的象与一次函数 的象交于点.
∴反比例函数象分布在第一、三象限,点A、B不在同一象限内, 当点A在第三象限,点B在第一象限,且
故答案为:B.
根据反比例函数和一次函数的图象可知交点分别位于分别一、三象限,然后根据增减性逐一判断解题.
39.C
解:A、令 则 所以在实数范围内能分解因式;
B、令 则 所以在实数范围内能分解因式;
C、令 则 所以 在实数范围内不能分解因式;
D、令 则 当 时, 所以 在实数范围内能分解因式.
故答案为:C.
根据二次多项式在实数范围内可以分解因式当且仅当其判别式 Δ=b2 4ac大于或等于0逐项判断解题.
40.B
解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、不是轴对称图形,也不是中心对称图形,故本选项错误;
C、是轴对称图形,不是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
根据轴对称图形与中心对称图形的概念“ 轴对称图形是指一个图形沿一条直线折叠,直线两旁的部分能够互相重合;而中心对称图形是指一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合 ”对各选项分析判断后利用排除法求解.
41.D
解:故 和 不互为相反数,原选项不符合题意;
故 和|4|不互为相反数,原选项不符合题意;
和 不互为相反数,原选项不符合题意;
故 和 互为相反数,原选项符合题意;
故答案为:D.
根据相反数的定义和化简绝对值逐项排除即可.
42.B
解:如图所示,连接.
中,
为的中点
中,
关于直线对称
设,则
中,,即:
整理得:,即:
是定值,
为定值.
故答案为:B.
由于轴对称图形的对应角相等,结合旋转的定义可推导出是直角,则是和的公共斜边,由直角三角形斜边上的中线等于斜边的一半及勾股定理可表示出的平方值,进而可表示出的平方值,此时可设出的长,则可分别表示出的长,利用勾股定理可得出,由于只知道是定值,即都是变量,所以线段的值不固定,但由于则可继续表示出的值,此时恰好得出的值是的一半,则只有是定值.
43.C
解:反比例函数
异号,即双曲线的两个分支分别在第二、四象限
(1)当时
当时,
当且时,
(2)当时
当时,
当且时,
综上所述:
A、若,则或,结果错误;
B、若,则或,结果错误;
C、若,则,即结果正确;
D、若,则,结果错误;
故答案为:C.
由于反比例系数,所以与符号相反,当时,与异号,则必然有与异号,即,故选项C正确;当时,应分类讨论,若两点都在第二象限,则与同号,此时;若两点分别在第二和第四象限,则与异号,此时;反之亦然,故选项都错误;当时,则与同号,则两点在同一象限,即与也同号,则,故选项D错误。
44.C
解:由题意知:
设,则
解得:
正方形ABCD的周长为
故答案为:C.
求正方形的周长,实质是求边长的值;由于图中四个直角三角形全等,则实质告诉了中两直角边与的和与差,则容易求得与的值,再利用勾股定理即可求出的值。
45.A
解:
,即点为中点
,即
故答案为:A.
由于位似图形是相似图形,且其中一组对应边可知,则利用相似比可确定点为中点,又点坐标已知,可借助中点公式直接求出点的坐标。
46.B
47.C
解:A、,结果错误;
B、,结果错误;
C、,结果正确;
D、,结果错误;
故答案为:C.
整式运算中首先要牢记合并同类项法则,即字母与字母的指数都不变,只把系数加减;其次要熟练使用幂的一些运算,如:
48.A
解:A、主视图,正确;
B、是从物体后面观察到的视图,不符合题意;
C、无论从哪个方向观察也得不到这个视图,不符合题意;
D、是左视图,不符合题意
故答案为:A.
主视图是指从物体正面观察得到的视图,左视图是指从物体从左边观察得到的视图,主视图是指从物体上面观察得到的视图.
49.D
解:
故答案为:D.
负数比较大小,绝对值大的反而小。
50.B
解:用科学记数法表示35000000是:3.5×107
故答案为:B.
科学记数法表示一个绝对值大于或等于1的数可以写成a×10n的形式,其中1≤<10,n等于原数的整数位数减1,据此即可解决问题.
同课章节目录
