专项2 填空题1(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项2 填空题1(浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 13:20:10 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项2 填空题1(浙江中考真题+中考模拟)
一、填空题
1.(2024·浙江)(1)若,,且,则的最小值为 .
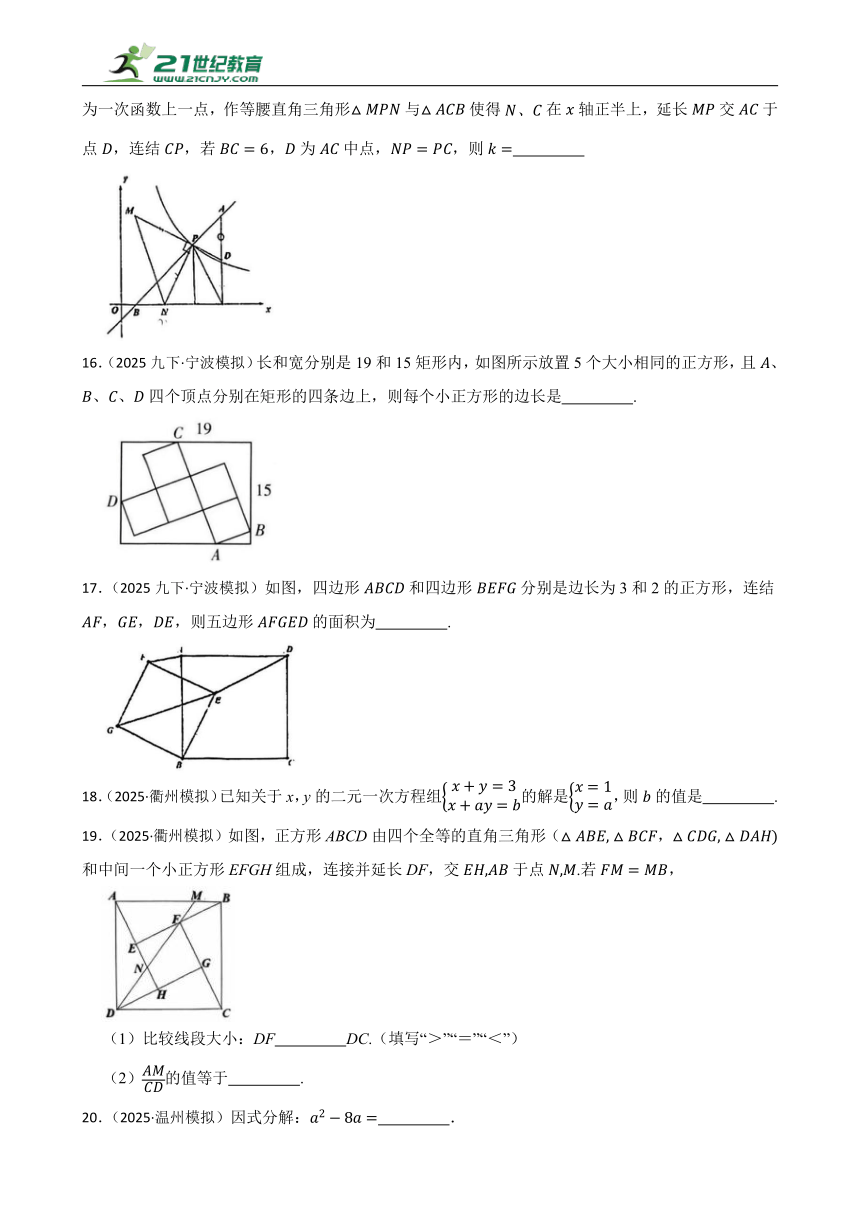
(2)如图,是的外接圆,点D是半圆弧的中点,交延长线于点E,连结,.若与的面积比为,则 .
2.(2024·浙江)已知实数a,b满是,则的最大值为 .
3.(2024·浙江)一组数据的平均数为5,方差为16,n是正整数,则另一组数据的标准差是 .
4.(2025·杭州模拟)因式分解: .
5.(2025九下·钱塘模拟)已知二次函数,当时,函数值 .
6.(2025·新昌模拟)如图,水暖管横截面是圆,当半径的水暖管有积水(阴影部分),水面的宽度为,则积水的最大深度是 .
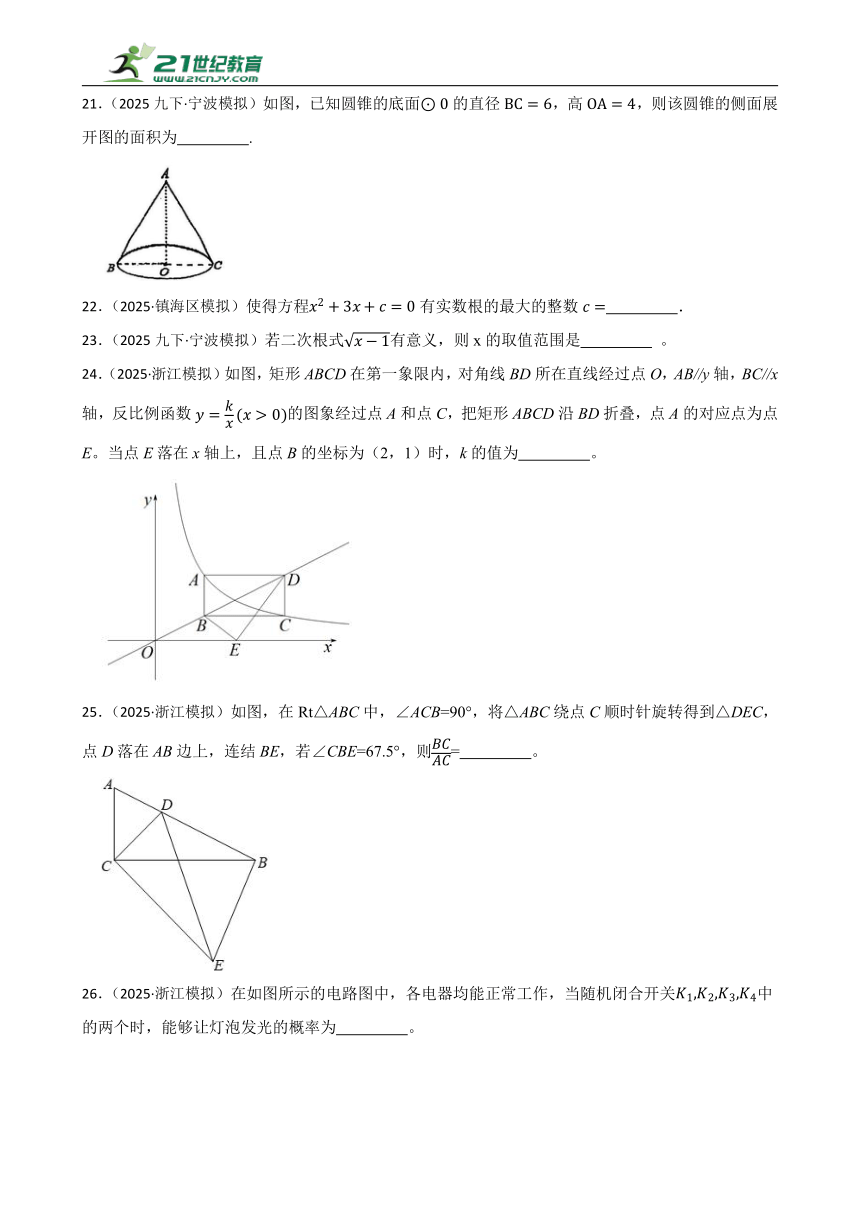
7.(2025·杭州模拟)一个不透明的袋子中装有四个小球,它们除了分别标有的数字1,2,3,4不同外,其它完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之和为5的概率是 .
8.(2025九下·浙江模拟)七巧板是中国古代人民创造的益智玩具,被誉为“东方魔板”.小明用一个边长为4的正方形制作出如图1的七巧板,再用这副七巧板拼出了如图2的“灵蛇献瑞”图.过该图形的三个顶点作圆,则这个圆的半径长为 .
9.(2025九下·浙江模拟)如图,在一张矩形纸片中,,分别是和的中点.现将纸片按如图方式折叠,使点与上的点重合.若平分,则的长为 .
10.(2025九下·浙江模拟)有12张卡片,每张卡片上分别写有不同的从1到12的一个自然数.从中任意抽出一张卡片,则这张卡片上的数既是3的倍数又是偶数的概率是 .
11.(2025九下·浙江模拟)如图,是的直径.点在上,是的切线,且为切点.已知,则 .
12.(2025九下·浙江模拟)当x 时,分式值为0.
13.(2025九下·浙江模拟)分解因式: -9= .
14.(2025·浙江模拟)如图,在等腰三角形ABC中,AB=AC,经过A,B两点的⊙O与边AC切于点A,与边BC交于点D,AE为⊙O直径,连结DE,若∠C=37°,则∠BDE的度数为 。
15.(2025九下·宁波模拟)如图所示,已知一次函数与反比例函数交于点为一次函数上一点,作等腰直角三角形与使得在轴正半上,延长交于点,连结,若,为中点,,则
16.(2025九下·宁波模拟)长和宽分别是19和15矩形内,如图所示放置5个大小相同的正方形,且、、、四个顶点分别在矩形的四条边上,则每个小正方形的边长是 .
17.(2025九下·宁波模拟)如图,四边形和四边形分别是边长为3和2的正方形,连结,,,则五边形的面积为 .
18.(2025·衢州模拟)已知关于x,y的二元一次方程组的解是,则的值是 .
19.(2025·衢州模拟)如图,正方形ABCD由四个全等的直角三角形(,和中间一个小正方形EFGH组成,连接并延长DF,交于点.若,
(1)比较线段大小:DF DC.(填写“>”“=”“<”)
(2)的值等于 .
20.(2025·温州模拟)因式分解: .
21.(2025九下·宁波模拟)如图,已知圆锥的底面的直径,高,则该圆锥的侧面展开图的面积为 .
22.(2025·镇海区模拟)使得方程有实数根的最大的整数 .
23.(2025九下·宁波模拟)若二次根式有意义,则x的取值范围是 。
24.(2025·浙江模拟)如图,矩形ABCD在第一象限内,对角线BD所在直线经过点O,AB//y轴,BC//x轴,反比例函数的图象经过点A和点C,把矩形ABCD沿BD折叠,点A的对应点为点E。当点E落在x轴上,且点B的坐标为(2,1)时,k的值为 。
25.(2025·浙江模拟)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在AB边上,连结BE,若∠CBE=67.5°,则= 。
26.(2025·浙江模拟)在如图所示的电路图中,各电器均能正常工作,当随机闭合开关中的两个时,能够让灯泡发光的概率为 。
27.(2025·衢州模拟)不等式的解是 .
28.(2025·浙江模拟)已知是方程的一个解,则k的值是 。
29.(2025·温州模拟)如图,点E,F分别在的边AB,CD上,连结DE,EF,点关于EF的对称点恰好在AB的延长线上,连结FG交BC于点.若,则 ,AE= .
30.(2025·温州模拟)如图,将Rt沿斜边AB向右平移得到与DF交于点,延长AC,EF交于点,连结GH.若,则AE的长为 .
31.(2025·温州模拟)一个布袋里只有红色、黄色、黑色三种球,它们除颜色外其余都相同,红球、黄球、黑球的个数之比为5:6:7.从布袋里任意摸出1个球,该球为黑球的概率是 .
32.(2025·温州模拟)如图,AB是半圆的直径,为AB延长线上一点,CD切半圆于点,连结OD,BD.若,则等于 度.
33.(2025·温州模拟)方程组的解为 .
34.(2025·衢州模拟)如图,直线BC与相切于点C,点A在上,AB⊥BC于点B.若AB=3,BC=6,则的半径为 cm.
35.(2025·衢州模拟)如图,转盘的白色扇形和灰色扇形的圆心角分别为和.让转盘自由转动一次,指针落在白色区域的概率是 .
36.(2025·衢州模拟)二次根式 中,a的取值范围是 .
37.(2025·鹿城模拟)小周要在一块三角形钢板中裁出一个矩形,裁剪方案如图所示,顶点、在边上,顶点,分别在边、上,已知,,,则当矩形的面积最大时, .
38.(2025·鹿城模拟)如图,,是的切线,切点分别是,,如果,那么的度数等于 .
39.(2025·镇海区模拟)如图,四边形是平行四边形,已知,,则 .
40.(2025·鹿城模拟)如图,点D、E分别为的中点,平分交于点F,若,则 .
41.(2025·钱塘模拟)如图,已知四边形内接于,延长,交于点.若,,则圆的半径为 .
42.(2025·钱塘模拟)如图,在扇形中,过的中点作,垂足分别为.已知,则图中阴影部分的面积为 (结果保留).
43.(2025·衢江模拟)如图,在中,将沿弦翻折,连结并延长交翻折后的弧于点,连结,若,,则的长为 .
44.(2025·衢江模拟)如图,在中,,点是边上的一点,满足.若,则的度数为 °.(请用含的代数式表示)
45.(2025·衢江模拟)已知圆锥的母线长为,底面半径为,则这个圆锥的侧面积为 .
46.(2025·衢江模拟)一只不透明的袋中装有8个白球和若干个红球,这些球除颜色外都相同,搅匀后每次随机从袋中摸出一个球,记下颜色后放回袋中.通过大量重复摸球试验后发现,摸到白球的频率是,则袋中约有红球 个.
47.(2025·镇海区模拟)已知正方形中,射线与边交于点,过点分别作射线的垂线,垂足分别为.设,若,则的最小值为 .
48.(2025·镇海区模拟)已知是镜子,球在两镜子之间的地面上.球在镜子中的像为,在中的像为.若镜子,之间的距离为66,则 .
49.(2025·镇海区模拟)已知如下的两组数据:
第一组:20,21,22,25,24,23;
第二组:20,21,23,25,,26.
若两组数据的中位数相等,实数 .
50.(2025·镇海区模拟)方程的解是 .
答案解析部分
1.;
2.55
3.12
4.a(a-4)
a2﹣4a=a(a﹣4).
故答案为a(a﹣4).
直接把公因式a提出来即可.
5.0
6.
7.
解:列出摸出的2球的树从图如下所示:
总共有12种情况,两球数字之和为5的情况有4种,故概率为P=
故答案为:.
利用树众图将可能所有情况列出,即可求出和为5的概率.
8.
解:如图2,设圆心为O,延长AF交PH于点E,交⊙O于点D, 连接EI,
∴四边形EFGH是平行四边形,且平行四边形 平行四边形BILK,
且
∴四边形EILH是平行四边形,
∵大正方形的边长为4,
且
∴EI垂直平分BC,
∴圆心O在EI上,
∴EI垂直平分AD,
,
连接OD、OB, 则
解得
∴这个圆的半径长为
故答案为:
在图2中标出相应的字母,设圆心为O,延长AF交PH于点E,交⊙O于点D,连接EI,则四边形EFGH是平行四边形,且 可证明四边形EILH是平行四边形,由大正方形的边长为4, 可知 则 得. 则EI垂直平分BC,所以圆心O在EI上,则EI垂直平分AD,连接OD、OB,由 根据勾股定理求得即可求出OD长于是得到问题的答案.
9.
解:过点G作 于M,
∵E, F分别是AD和BC的中点,
∵AG平分 ,
由折叠可知,
故答案为:
过点G作于M,则 由AG平分 可得 由折叠可知, ,再由勾股定理得到长,则 进而求得AB长.
10.
解:从1到12的自然数中,既是3的倍数又是偶数的6,12, 共2种结果,
故答案为:
从1到12的自然数中,既是3的倍数又是偶数的6,12,共2种结果,据此计算即可.
11.67
解:∵AD是⊙O的直径, 点B在⊙O上, AC是⊙O的切线, A为切点.
在中,
故答案为:67.
根据切线的性质得到 由此得到 根据AD是直径可得 由直角三角形两锐角互余即可求解.
12.=-1
解:∵分式 值为0,
且
解得
故答案为:=-1.
若分式的值为零,需同时具备两个条件:①分子的值为0,②分母的值不为0,这两个条件缺一不可.
13.
-9= .
14.16
解:∵AB=AC,∠C=37°,
∴ ∠B=∠C=37°,
∴∠BAC=180°-∠B-∠C=106°.
∵⊙O与边AC切于点A,
∴∠CAE=90°,
∴∠BDE=∠BAE=∠BAC-∠CAE=16°.
故答案为:16.
先根据等边对等角,求得∠B,再利用三角形内角和定理求得∠BAC,然后利用切线的性质证得∠CAE=90°,再用两角之差求得∠BDE.
15.20
解:过点P作PH⊥x轴于点H,延长HP,过点M作MG⊥PH交PH于点G,
令y=0.则x-1=0,解得x=1,
∴点B的坐标为(1,0),∴OB=1,
∵BC=6,
∴OC=OB+BC=1+6=7,∴点C的坐标为(7,0),
把x=7代入得y=7-1=6,∴点A的坐标为(7,6),
又∵D是AC的中点,∴点D的坐标为(7,3),
又∵AC=6=BC,∴∠ABC=∠CAB=45°,
∵PH⊥x轴,
∴∠PHB=90°,
∴△PBH为等要直角三角形,
∴BH=PH,
设OH=m,则BH=OH-OB=m-1,
∴PH=BH=m-1,即点P的坐标为(m,m-1),
∵△PMN是等腰直角三角形,
∴MP=PN,
∵MG⊥PH,PH⊥x轴,
∴∠G=∠MPN=∠PHB=90°,
∴∠GMP+∠GPM=∠NPH=∠GPM=90°,
∴∠GMP=∠NPH,
∴△MPG≌△PNH,
∴MG=PH=m-1,PG=NH=CH=OC-OH=7-m,
∴NH=CH=PG,
∵,,
∴点M的坐标为(1,6),
设直线MD的解析式为y=kx+b,代入得:
,解得,
∴直线MD的解析式为,
把P(m,m-1)代入得到,解得m=5,
∴点P的坐标为(5,4),
把点P(5,4)代入得到k=5×4=20,
故答案为,20.
过点P作PH⊥x轴于点H,延长HP,过点M作MG⊥PH交PH于点G,设OH=m,即可得到△MPG≌△PNH,求出点M的坐标,然后求出直线MD的解析式,再求出点P的坐标,代入反比例函数解析式即可解题.
16.
解:
设正方形边长为x,假设AC在矩形里与其它线段分别交于点T和点P,过T做平行于点C所在的矩形边,交矩形另外两边于点E和点F;过点P做平行于点B所在的矩形边,交矩形另外两边于点J和点H;EF和JH相交于点O, EF垂直于JH, 设EF与DT边成的角为θ,则PJ与PC边成的角也为θ,
在 中,
可得 ①
解得
两边平方相加得
所以正方形的边长
故答案为:.
如图,设正方形边长为x,设EF与DT边成的角为θ,则PJ与PC边成的角也为θ,利用三角函数值表示出EF和JH的值求出然后根据一个角的正弦与余弦的平方和为1求出x值即可.
17.4.5
解:如图, 过点A作. 于T,连接AE,过点E作 于P,
设
∵四边形ABCD和四边形BEFG为正方形,
,
.
故答案为: 4.5.
如图,过点A作. 于T, 连接AE,过点E作 于P, 设. 由勾股定理得 利用余弦列式为 可表示BN的长,证明 利用余弦的定义可得AT的长,最后由面积和即可解答.
18.5
解:∵ 关于x,y的二元一次方程组的解是,
∴,解得:.
故答案为:5.
根据方程组解的意义,将解代入方程组,转化为关于字母参数的方程求解.
19.(1)=
(2)
解:(1)∵FM=MB,
∴∠MFB=∠MBF=∠EFN,
∵∠MBF+∠FBC=90°,
∠EFN+∠DFC=90°,
∴∠FBC=∠DFC.
∵△ABC≌△CDG,
∴∠FBC=∠DFC=∠DCF,
∴DF=DC.
故答案为:=.
(2)∵四边形ABCD是正方形,
∴AB=BC=CD=AD=x,MB=y,
∵DM2=AD2+AM2,
∴(x+y)2=x2+(x-y)2.解得:x2=4xy.
∵x>0,
∴x=4y,
∴.
故答案为:.
(1)先根据等腰三角形的性质以及对顶角相等,证明∠FBC=∠DFC,再结合等角的余角相等,证得∠FBC=∠DFC,然后利用全等三角形的性质证得∠FBC=∠DFC=∠DCF,再利用等角对等边可得DF=DC;
(2)先用x、y表示出AM,DM,再利用勾股定理求得x与y的关系,然后求得.
20.
解:
故答案为:.
分解因式的一般策略是“一提二套”,即当多项式的各项都有公因式时,先提公因式,再考虑对另一个因式套用乘法公式继续分解因式,直到每一个因式不能再分解为止.
21.
解:在 中,
所以这个圆锥的侧面展开图的面积
故答案为:.
先利用勾股定理计算出AB,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解即可.
22.2
23.x≥1
根据二次根式有意义的条件,x﹣1≥0,∴x≥1.故答案为:x≥1.
根据二次根式的性质可知,被开方数大于等于0,列出不等式即可求出x的取值范围.
24.
解:设E(x,0),
∵AB//y轴,BC//x轴,点B的坐标为(2,1), 反比例函数的图象经过点A和点C,
∴A(2,),C(k,1),
∴AB=-1,
∵四边形ABCD是矩形,
∴D(k,),
∴AD=BC=k-2.
∵把矩形ABCD沿BD折叠,点A的对应点为点E,
∴BE=AB=-1,DE=ADk-2.
∴BE2=(x-2)2+12=(-1)2,
DE2=(x-k)2+()2=(k-2)2,
解得:x1=2,x2=.
∵ 反比例函数,,
∴k=4x-8>0,解得:x>2.
∴x=,
∴k=4x-8=.
故答案为:.
先根据矩形的性质,用k表示出A,C,D,再计算BE2与DE2,求得x,根据x的范围确定x的值,再求出k.
25.
解:设BD=x,
∵ 将△ABC绕点C顺时针旋转得到△DEC,
∴CE=BC,AC=CD,∠ACB=∠DCE=90 ° ,∠ABC=∠CED.
∵ ∠CBE=67.5°,
∴∠BEC=∠CBE=67.5°,
∴∠BCE=180°-∠BEC-∠CBE=45°.
∴∠BCD=∠DCE-∠BCE=45°.
∴∠ACD=∠ACB-∠BCD=45°.
∴∠A=∠ADC=(180°-∠ACD)=67.5°.
∴∠ABC=∠CED=90°-∠A=22.5°.
∴∠DBE=∠CBE+∠ABC=90°,∠DEB=∠CEB-∠CED=45°.
∴△BDE是等腰直角三角形,
∴BD=BE,
∴DE=AB=.
∴AD=AB-BD=.
∵∠A=∠ADC=∠CBE=∠CEB=67.5°,
∴△CBE∽△CAD.
∴.
故答案为:.
先利用旋转的性质,证得CE=BC,AC=CD,∠ACB=∠DCE=90 ° ,∠ABC=∠CED.再利用等边对等角求得∠BEC,然后证明△BDE是等腰直角三角形,用x表示出DE和AD,再利用△CBE∽△CAD,列出比例式,求得.
26.
解:画树状图.
共有12种等可能的结果,其中能够让灯泡发光的结果有8种,
∴能够让灯泡发光的概率.
故答案为:.
先画树状图,求出所有等可能结果数与符合条件的结果数,再利用概率公式求解.
27.
解:,
去分母,得2x+3>4,
移项,得2x>4-3,
合并同类项,得2x>1,
即x>.
故答案为:.
先去分母,再移项,合并同类项,系数化为1求解.
28.4
解:∵是方程的一个解,
∴1+2k=9,解得:k=4.
故答案为:4.
根据方程解的意义,转化为k的方程求解.
29.;
解:如图所示,连接DG交EF于点O.
关于直线EF对称
四边形ABCD是平行四边形
四边形DEGF是菱形
设,则
四边形ABCD和四边形DEGF都是平行四边形
故答案分别为:和.
第一空:由轴对称的性质知EF垂直平分DG,则FD等于FG,再等腰三角形三线合一知FE平分,由于平行四边形的对边平行,由平行线的性质结合等量代换得等于,则GE等于GF,可将线段GH与EG的比转化为GH与FG的比,从而利用比例的基本性质得到FH与GH的比值;第二空:由第一空的推理可得四边形DEGF是菱形,则可设FH等于3a,则GH等于5a,则DE、EG、FG都是8a,此时利用平行四边形的对边平行,可借助内错角相等证明与相似,再借助同位角相等证明与相似,由于CF已知,两组三角形的相似比可以计算出来,则可先求出BG的值,进而求出AE的值.
30.8
解:如图,连接CF.
、
四边形CHFG是平行四边形
是矩形
四边形ADFC是平行四边形
故答案为:8.
由于平移不改变图形的形状与大小,且平移前后对应线段平行且相等,或在同一条直线上,因此可连接CF,则四边形ADFC是平行四边形;同理四边形CHFG也是平行四边形,由于已知是直角,则平行四边形CHFG还是矩形,则对角线CF等于GH,则AD等于3,结合已知得AB等于5;由于DE等于AB等于5,则AE可求.
31.
解:
故答案为:.
直接利用简单随机事件概率的求解方法计算即可.
32.130
解:是的切线
,即
故答案为:130.
由于切线垂直于过切点的半径,因此可知等于90度;由于已知,则可求;由于半径处处相等,因此等于;最后利用外角的性质可直接求出度数.
33.
解:
得:
把代入得:
原方程组的解为
故答案为:.
解二元一次方程组时,当两个方程中某一个未知数的系数相等或互为相反数时,可直接利用加减消元法求解.
34.
解:如图,连结OA,OC,过点A作AD⊥OC于点D,设的半径为r,
∵直线BC与相切于点C,
∴BC⊥OC,
∵AB⊥BC于点B ,
∴四边形ABCD是矩形,
∴CD=AB=3,AD=BC=6,
∴OD=r-3,
∵OA2=DA2+OD2,
∴r2=62+(r-3)2,解得:r=.
故答案为:.
先证明四边形ABCD是矩形,再利用勾股定理,得到关于r的方程求解.
35.
解:∵ 转盘的白色扇形和灰色扇形的圆心角分别为和,
∴转动一次,指针落在白色区域的概率为.
故答案为:.
利用概率公式求解.
36.a≥1
解:由题意得,a﹣1≥0,
解得,a≥1,
故答案为:a≥1.
根据二次根式有意义的条件列出不等式,解不等式即可.
37.
解:过点作于点,交于点,
,
,
即,
解得,
四边形为矩形,
,
,
,
四边形为矩形,
,
,
,
,
,即,
,
,
故当时,矩形面积最大,
,
此时,
故答案为:.
过点作于点,交于点,根据三角形ABC的面积等于40看求出的值,由“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的对应边的比相等可得比例式,根据比例式可将DE用含DG的代数式表示出来,于是,将S矩形DEFG与DG之间的函数关系式配成顶点式,然后根据二次函数的性质可求解.
38.
解:连接,,
、是的切线,切点分别是、,
,
,
,
.
故答案为:.
由切线的性质“圆的切线垂直于经过切点的半径”可得,根据圆周角定理“同弧所对的圆周角等于它所对的圆心角的一半”可得∠AOB=2∠C,然后根据四边形内角和定理可求解.
39.
40.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
41.7
42.
43.
解:延长交于点D,过点B作于点H,连接,
∵和是圆周角所对的弧,
∴,
∴,
∴,
设,
∴,,
∵,
∴,
∵是直径,
∴,
∵,
∴,
∴,
∴,
在中,,
∴,
整理得,
解得或(舍去),
∴,,
在,,
故答案为:.
延长交于点D,过点B作于点H,连接,先根据“在同圆或等圆中,相等的圆周角所对的弧相等”,得到,即,根据等腰三角形三线合一性质,得到,设,则,结合已知根据“有两个角对应相等的两个三角形相似”可得,由相似三角形的对应边的比相等可得比例式,整理可得,在中,利用勾股定理得到,即,解方程求出a的值,在Rt△ABH中,用勾股定理计算即可求解.
44.
解:设,
∵,
∴,
∵,
∴,
由三角形内角和定理得,
即,
∴,
故答案为:.
设,由等边对等角得∠B=,在△ABC中,根据三角形内角和定理可得关于x的方程,解方程即可求解.
45.
解:由题意,得:圆锥的侧面积为;
故答案为:.
根据圆锥的侧面积公式计算即可求解.
46.12
解:设红球有x个,由题意可得,
,
解得:,
经检验:是方程的解,
故答案为:12.
设红球有x个,根据频率=红球个数÷总数可得关于x的方程,解方程即可求解.
47.
48.132
49.22
50.
专项2 填空题1(浙江中考真题+中考模拟)
一、填空题
1.(2024·浙江)(1)若,,且,则的最小值为 .
(2)如图,是的外接圆,点D是半圆弧的中点,交延长线于点E,连结,.若与的面积比为,则 .
2.(2024·浙江)已知实数a,b满是,则的最大值为 .
3.(2024·浙江)一组数据的平均数为5,方差为16,n是正整数,则另一组数据的标准差是 .
4.(2025·杭州模拟)因式分解: .
5.(2025九下·钱塘模拟)已知二次函数,当时,函数值 .
6.(2025·新昌模拟)如图,水暖管横截面是圆,当半径的水暖管有积水(阴影部分),水面的宽度为,则积水的最大深度是 .
7.(2025·杭州模拟)一个不透明的袋子中装有四个小球,它们除了分别标有的数字1,2,3,4不同外,其它完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之和为5的概率是 .
8.(2025九下·浙江模拟)七巧板是中国古代人民创造的益智玩具,被誉为“东方魔板”.小明用一个边长为4的正方形制作出如图1的七巧板,再用这副七巧板拼出了如图2的“灵蛇献瑞”图.过该图形的三个顶点作圆,则这个圆的半径长为 .
9.(2025九下·浙江模拟)如图,在一张矩形纸片中,,分别是和的中点.现将纸片按如图方式折叠,使点与上的点重合.若平分,则的长为 .
10.(2025九下·浙江模拟)有12张卡片,每张卡片上分别写有不同的从1到12的一个自然数.从中任意抽出一张卡片,则这张卡片上的数既是3的倍数又是偶数的概率是 .
11.(2025九下·浙江模拟)如图,是的直径.点在上,是的切线,且为切点.已知,则 .
12.(2025九下·浙江模拟)当x 时,分式值为0.
13.(2025九下·浙江模拟)分解因式: -9= .
14.(2025·浙江模拟)如图,在等腰三角形ABC中,AB=AC,经过A,B两点的⊙O与边AC切于点A,与边BC交于点D,AE为⊙O直径,连结DE,若∠C=37°,则∠BDE的度数为 。
15.(2025九下·宁波模拟)如图所示,已知一次函数与反比例函数交于点为一次函数上一点,作等腰直角三角形与使得在轴正半上,延长交于点,连结,若,为中点,,则
16.(2025九下·宁波模拟)长和宽分别是19和15矩形内,如图所示放置5个大小相同的正方形,且、、、四个顶点分别在矩形的四条边上,则每个小正方形的边长是 .
17.(2025九下·宁波模拟)如图,四边形和四边形分别是边长为3和2的正方形,连结,,,则五边形的面积为 .
18.(2025·衢州模拟)已知关于x,y的二元一次方程组的解是,则的值是 .
19.(2025·衢州模拟)如图,正方形ABCD由四个全等的直角三角形(,和中间一个小正方形EFGH组成,连接并延长DF,交于点.若,
(1)比较线段大小:DF DC.(填写“>”“=”“<”)
(2)的值等于 .
20.(2025·温州模拟)因式分解: .
21.(2025九下·宁波模拟)如图,已知圆锥的底面的直径,高,则该圆锥的侧面展开图的面积为 .
22.(2025·镇海区模拟)使得方程有实数根的最大的整数 .
23.(2025九下·宁波模拟)若二次根式有意义,则x的取值范围是 。
24.(2025·浙江模拟)如图,矩形ABCD在第一象限内,对角线BD所在直线经过点O,AB//y轴,BC//x轴,反比例函数的图象经过点A和点C,把矩形ABCD沿BD折叠,点A的对应点为点E。当点E落在x轴上,且点B的坐标为(2,1)时,k的值为 。
25.(2025·浙江模拟)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在AB边上,连结BE,若∠CBE=67.5°,则= 。
26.(2025·浙江模拟)在如图所示的电路图中,各电器均能正常工作,当随机闭合开关中的两个时,能够让灯泡发光的概率为 。
27.(2025·衢州模拟)不等式的解是 .
28.(2025·浙江模拟)已知是方程的一个解,则k的值是 。
29.(2025·温州模拟)如图,点E,F分别在的边AB,CD上,连结DE,EF,点关于EF的对称点恰好在AB的延长线上,连结FG交BC于点.若,则 ,AE= .
30.(2025·温州模拟)如图,将Rt沿斜边AB向右平移得到与DF交于点,延长AC,EF交于点,连结GH.若,则AE的长为 .
31.(2025·温州模拟)一个布袋里只有红色、黄色、黑色三种球,它们除颜色外其余都相同,红球、黄球、黑球的个数之比为5:6:7.从布袋里任意摸出1个球,该球为黑球的概率是 .
32.(2025·温州模拟)如图,AB是半圆的直径,为AB延长线上一点,CD切半圆于点,连结OD,BD.若,则等于 度.
33.(2025·温州模拟)方程组的解为 .
34.(2025·衢州模拟)如图,直线BC与相切于点C,点A在上,AB⊥BC于点B.若AB=3,BC=6,则的半径为 cm.
35.(2025·衢州模拟)如图,转盘的白色扇形和灰色扇形的圆心角分别为和.让转盘自由转动一次,指针落在白色区域的概率是 .
36.(2025·衢州模拟)二次根式 中,a的取值范围是 .
37.(2025·鹿城模拟)小周要在一块三角形钢板中裁出一个矩形,裁剪方案如图所示,顶点、在边上,顶点,分别在边、上,已知,,,则当矩形的面积最大时, .
38.(2025·鹿城模拟)如图,,是的切线,切点分别是,,如果,那么的度数等于 .
39.(2025·镇海区模拟)如图,四边形是平行四边形,已知,,则 .
40.(2025·鹿城模拟)如图,点D、E分别为的中点,平分交于点F,若,则 .
41.(2025·钱塘模拟)如图,已知四边形内接于,延长,交于点.若,,则圆的半径为 .
42.(2025·钱塘模拟)如图,在扇形中,过的中点作,垂足分别为.已知,则图中阴影部分的面积为 (结果保留).
43.(2025·衢江模拟)如图,在中,将沿弦翻折,连结并延长交翻折后的弧于点,连结,若,,则的长为 .
44.(2025·衢江模拟)如图,在中,,点是边上的一点,满足.若,则的度数为 °.(请用含的代数式表示)
45.(2025·衢江模拟)已知圆锥的母线长为,底面半径为,则这个圆锥的侧面积为 .
46.(2025·衢江模拟)一只不透明的袋中装有8个白球和若干个红球,这些球除颜色外都相同,搅匀后每次随机从袋中摸出一个球,记下颜色后放回袋中.通过大量重复摸球试验后发现,摸到白球的频率是,则袋中约有红球 个.
47.(2025·镇海区模拟)已知正方形中,射线与边交于点,过点分别作射线的垂线,垂足分别为.设,若,则的最小值为 .
48.(2025·镇海区模拟)已知是镜子,球在两镜子之间的地面上.球在镜子中的像为,在中的像为.若镜子,之间的距离为66,则 .
49.(2025·镇海区模拟)已知如下的两组数据:
第一组:20,21,22,25,24,23;
第二组:20,21,23,25,,26.
若两组数据的中位数相等,实数 .
50.(2025·镇海区模拟)方程的解是 .
答案解析部分
1.;
2.55
3.12
4.a(a-4)
a2﹣4a=a(a﹣4).
故答案为a(a﹣4).
直接把公因式a提出来即可.
5.0
6.
7.
解:列出摸出的2球的树从图如下所示:
总共有12种情况,两球数字之和为5的情况有4种,故概率为P=
故答案为:.
利用树众图将可能所有情况列出,即可求出和为5的概率.
8.
解:如图2,设圆心为O,延长AF交PH于点E,交⊙O于点D, 连接EI,
∴四边形EFGH是平行四边形,且平行四边形 平行四边形BILK,
且
∴四边形EILH是平行四边形,
∵大正方形的边长为4,
且
∴EI垂直平分BC,
∴圆心O在EI上,
∴EI垂直平分AD,
,
连接OD、OB, 则
解得
∴这个圆的半径长为
故答案为:
在图2中标出相应的字母,设圆心为O,延长AF交PH于点E,交⊙O于点D,连接EI,则四边形EFGH是平行四边形,且 可证明四边形EILH是平行四边形,由大正方形的边长为4, 可知 则 得. 则EI垂直平分BC,所以圆心O在EI上,则EI垂直平分AD,连接OD、OB,由 根据勾股定理求得即可求出OD长于是得到问题的答案.
9.
解:过点G作 于M,
∵E, F分别是AD和BC的中点,
∵AG平分 ,
由折叠可知,
故答案为:
过点G作于M,则 由AG平分 可得 由折叠可知, ,再由勾股定理得到长,则 进而求得AB长.
10.
解:从1到12的自然数中,既是3的倍数又是偶数的6,12, 共2种结果,
故答案为:
从1到12的自然数中,既是3的倍数又是偶数的6,12,共2种结果,据此计算即可.
11.67
解:∵AD是⊙O的直径, 点B在⊙O上, AC是⊙O的切线, A为切点.
在中,
故答案为:67.
根据切线的性质得到 由此得到 根据AD是直径可得 由直角三角形两锐角互余即可求解.
12.=-1
解:∵分式 值为0,
且
解得
故答案为:=-1.
若分式的值为零,需同时具备两个条件:①分子的值为0,②分母的值不为0,这两个条件缺一不可.
13.
-9= .
14.16
解:∵AB=AC,∠C=37°,
∴ ∠B=∠C=37°,
∴∠BAC=180°-∠B-∠C=106°.
∵⊙O与边AC切于点A,
∴∠CAE=90°,
∴∠BDE=∠BAE=∠BAC-∠CAE=16°.
故答案为:16.
先根据等边对等角,求得∠B,再利用三角形内角和定理求得∠BAC,然后利用切线的性质证得∠CAE=90°,再用两角之差求得∠BDE.
15.20
解:过点P作PH⊥x轴于点H,延长HP,过点M作MG⊥PH交PH于点G,
令y=0.则x-1=0,解得x=1,
∴点B的坐标为(1,0),∴OB=1,
∵BC=6,
∴OC=OB+BC=1+6=7,∴点C的坐标为(7,0),
把x=7代入得y=7-1=6,∴点A的坐标为(7,6),
又∵D是AC的中点,∴点D的坐标为(7,3),
又∵AC=6=BC,∴∠ABC=∠CAB=45°,
∵PH⊥x轴,
∴∠PHB=90°,
∴△PBH为等要直角三角形,
∴BH=PH,
设OH=m,则BH=OH-OB=m-1,
∴PH=BH=m-1,即点P的坐标为(m,m-1),
∵△PMN是等腰直角三角形,
∴MP=PN,
∵MG⊥PH,PH⊥x轴,
∴∠G=∠MPN=∠PHB=90°,
∴∠GMP+∠GPM=∠NPH=∠GPM=90°,
∴∠GMP=∠NPH,
∴△MPG≌△PNH,
∴MG=PH=m-1,PG=NH=CH=OC-OH=7-m,
∴NH=CH=PG,
∵,,
∴点M的坐标为(1,6),
设直线MD的解析式为y=kx+b,代入得:
,解得,
∴直线MD的解析式为,
把P(m,m-1)代入得到,解得m=5,
∴点P的坐标为(5,4),
把点P(5,4)代入得到k=5×4=20,
故答案为,20.
过点P作PH⊥x轴于点H,延长HP,过点M作MG⊥PH交PH于点G,设OH=m,即可得到△MPG≌△PNH,求出点M的坐标,然后求出直线MD的解析式,再求出点P的坐标,代入反比例函数解析式即可解题.
16.
解:
设正方形边长为x,假设AC在矩形里与其它线段分别交于点T和点P,过T做平行于点C所在的矩形边,交矩形另外两边于点E和点F;过点P做平行于点B所在的矩形边,交矩形另外两边于点J和点H;EF和JH相交于点O, EF垂直于JH, 设EF与DT边成的角为θ,则PJ与PC边成的角也为θ,
在 中,
可得 ①
解得
两边平方相加得
所以正方形的边长
故答案为:.
如图,设正方形边长为x,设EF与DT边成的角为θ,则PJ与PC边成的角也为θ,利用三角函数值表示出EF和JH的值求出然后根据一个角的正弦与余弦的平方和为1求出x值即可.
17.4.5
解:如图, 过点A作. 于T,连接AE,过点E作 于P,
设
∵四边形ABCD和四边形BEFG为正方形,
,
.
故答案为: 4.5.
如图,过点A作. 于T, 连接AE,过点E作 于P, 设. 由勾股定理得 利用余弦列式为 可表示BN的长,证明 利用余弦的定义可得AT的长,最后由面积和即可解答.
18.5
解:∵ 关于x,y的二元一次方程组的解是,
∴,解得:.
故答案为:5.
根据方程组解的意义,将解代入方程组,转化为关于字母参数的方程求解.
19.(1)=
(2)
解:(1)∵FM=MB,
∴∠MFB=∠MBF=∠EFN,
∵∠MBF+∠FBC=90°,
∠EFN+∠DFC=90°,
∴∠FBC=∠DFC.
∵△ABC≌△CDG,
∴∠FBC=∠DFC=∠DCF,
∴DF=DC.
故答案为:=.
(2)∵四边形ABCD是正方形,
∴AB=BC=CD=AD=x,MB=y,
∵DM2=AD2+AM2,
∴(x+y)2=x2+(x-y)2.解得:x2=4xy.
∵x>0,
∴x=4y,
∴.
故答案为:.
(1)先根据等腰三角形的性质以及对顶角相等,证明∠FBC=∠DFC,再结合等角的余角相等,证得∠FBC=∠DFC,然后利用全等三角形的性质证得∠FBC=∠DFC=∠DCF,再利用等角对等边可得DF=DC;
(2)先用x、y表示出AM,DM,再利用勾股定理求得x与y的关系,然后求得.
20.
解:
故答案为:.
分解因式的一般策略是“一提二套”,即当多项式的各项都有公因式时,先提公因式,再考虑对另一个因式套用乘法公式继续分解因式,直到每一个因式不能再分解为止.
21.
解:在 中,
所以这个圆锥的侧面展开图的面积
故答案为:.
先利用勾股定理计算出AB,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解即可.
22.2
23.x≥1
根据二次根式有意义的条件,x﹣1≥0,∴x≥1.故答案为:x≥1.
根据二次根式的性质可知,被开方数大于等于0,列出不等式即可求出x的取值范围.
24.
解:设E(x,0),
∵AB//y轴,BC//x轴,点B的坐标为(2,1), 反比例函数的图象经过点A和点C,
∴A(2,),C(k,1),
∴AB=-1,
∵四边形ABCD是矩形,
∴D(k,),
∴AD=BC=k-2.
∵把矩形ABCD沿BD折叠,点A的对应点为点E,
∴BE=AB=-1,DE=ADk-2.
∴BE2=(x-2)2+12=(-1)2,
DE2=(x-k)2+()2=(k-2)2,
解得:x1=2,x2=.
∵ 反比例函数,,
∴k=4x-8>0,解得:x>2.
∴x=,
∴k=4x-8=.
故答案为:.
先根据矩形的性质,用k表示出A,C,D,再计算BE2与DE2,求得x,根据x的范围确定x的值,再求出k.
25.
解:设BD=x,
∵ 将△ABC绕点C顺时针旋转得到△DEC,
∴CE=BC,AC=CD,∠ACB=∠DCE=90 ° ,∠ABC=∠CED.
∵ ∠CBE=67.5°,
∴∠BEC=∠CBE=67.5°,
∴∠BCE=180°-∠BEC-∠CBE=45°.
∴∠BCD=∠DCE-∠BCE=45°.
∴∠ACD=∠ACB-∠BCD=45°.
∴∠A=∠ADC=(180°-∠ACD)=67.5°.
∴∠ABC=∠CED=90°-∠A=22.5°.
∴∠DBE=∠CBE+∠ABC=90°,∠DEB=∠CEB-∠CED=45°.
∴△BDE是等腰直角三角形,
∴BD=BE,
∴DE=AB=.
∴AD=AB-BD=.
∵∠A=∠ADC=∠CBE=∠CEB=67.5°,
∴△CBE∽△CAD.
∴.
故答案为:.
先利用旋转的性质,证得CE=BC,AC=CD,∠ACB=∠DCE=90 ° ,∠ABC=∠CED.再利用等边对等角求得∠BEC,然后证明△BDE是等腰直角三角形,用x表示出DE和AD,再利用△CBE∽△CAD,列出比例式,求得.
26.
解:画树状图.
共有12种等可能的结果,其中能够让灯泡发光的结果有8种,
∴能够让灯泡发光的概率.
故答案为:.
先画树状图,求出所有等可能结果数与符合条件的结果数,再利用概率公式求解.
27.
解:,
去分母,得2x+3>4,
移项,得2x>4-3,
合并同类项,得2x>1,
即x>.
故答案为:.
先去分母,再移项,合并同类项,系数化为1求解.
28.4
解:∵是方程的一个解,
∴1+2k=9,解得:k=4.
故答案为:4.
根据方程解的意义,转化为k的方程求解.
29.;
解:如图所示,连接DG交EF于点O.
关于直线EF对称
四边形ABCD是平行四边形
四边形DEGF是菱形
设,则
四边形ABCD和四边形DEGF都是平行四边形
故答案分别为:和.
第一空:由轴对称的性质知EF垂直平分DG,则FD等于FG,再等腰三角形三线合一知FE平分,由于平行四边形的对边平行,由平行线的性质结合等量代换得等于,则GE等于GF,可将线段GH与EG的比转化为GH与FG的比,从而利用比例的基本性质得到FH与GH的比值;第二空:由第一空的推理可得四边形DEGF是菱形,则可设FH等于3a,则GH等于5a,则DE、EG、FG都是8a,此时利用平行四边形的对边平行,可借助内错角相等证明与相似,再借助同位角相等证明与相似,由于CF已知,两组三角形的相似比可以计算出来,则可先求出BG的值,进而求出AE的值.
30.8
解:如图,连接CF.
、
四边形CHFG是平行四边形
是矩形
四边形ADFC是平行四边形
故答案为:8.
由于平移不改变图形的形状与大小,且平移前后对应线段平行且相等,或在同一条直线上,因此可连接CF,则四边形ADFC是平行四边形;同理四边形CHFG也是平行四边形,由于已知是直角,则平行四边形CHFG还是矩形,则对角线CF等于GH,则AD等于3,结合已知得AB等于5;由于DE等于AB等于5,则AE可求.
31.
解:
故答案为:.
直接利用简单随机事件概率的求解方法计算即可.
32.130
解:是的切线
,即
故答案为:130.
由于切线垂直于过切点的半径,因此可知等于90度;由于已知,则可求;由于半径处处相等,因此等于;最后利用外角的性质可直接求出度数.
33.
解:
得:
把代入得:
原方程组的解为
故答案为:.
解二元一次方程组时,当两个方程中某一个未知数的系数相等或互为相反数时,可直接利用加减消元法求解.
34.
解:如图,连结OA,OC,过点A作AD⊥OC于点D,设的半径为r,
∵直线BC与相切于点C,
∴BC⊥OC,
∵AB⊥BC于点B ,
∴四边形ABCD是矩形,
∴CD=AB=3,AD=BC=6,
∴OD=r-3,
∵OA2=DA2+OD2,
∴r2=62+(r-3)2,解得:r=.
故答案为:.
先证明四边形ABCD是矩形,再利用勾股定理,得到关于r的方程求解.
35.
解:∵ 转盘的白色扇形和灰色扇形的圆心角分别为和,
∴转动一次,指针落在白色区域的概率为.
故答案为:.
利用概率公式求解.
36.a≥1
解:由题意得,a﹣1≥0,
解得,a≥1,
故答案为:a≥1.
根据二次根式有意义的条件列出不等式,解不等式即可.
37.
解:过点作于点,交于点,
,
,
即,
解得,
四边形为矩形,
,
,
,
四边形为矩形,
,
,
,
,
,即,
,
,
故当时,矩形面积最大,
,
此时,
故答案为:.
过点作于点,交于点,根据三角形ABC的面积等于40看求出的值,由“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的对应边的比相等可得比例式,根据比例式可将DE用含DG的代数式表示出来,于是,将S矩形DEFG与DG之间的函数关系式配成顶点式,然后根据二次函数的性质可求解.
38.
解:连接,,
、是的切线,切点分别是、,
,
,
,
.
故答案为:.
由切线的性质“圆的切线垂直于经过切点的半径”可得,根据圆周角定理“同弧所对的圆周角等于它所对的圆心角的一半”可得∠AOB=2∠C,然后根据四边形内角和定理可求解.
39.
40.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
41.7
42.
43.
解:延长交于点D,过点B作于点H,连接,
∵和是圆周角所对的弧,
∴,
∴,
∴,
设,
∴,,
∵,
∴,
∵是直径,
∴,
∵,
∴,
∴,
∴,
在中,,
∴,
整理得,
解得或(舍去),
∴,,
在,,
故答案为:.
延长交于点D,过点B作于点H,连接,先根据“在同圆或等圆中,相等的圆周角所对的弧相等”,得到,即,根据等腰三角形三线合一性质,得到,设,则,结合已知根据“有两个角对应相等的两个三角形相似”可得,由相似三角形的对应边的比相等可得比例式,整理可得,在中,利用勾股定理得到,即,解方程求出a的值,在Rt△ABH中,用勾股定理计算即可求解.
44.
解:设,
∵,
∴,
∵,
∴,
由三角形内角和定理得,
即,
∴,
故答案为:.
设,由等边对等角得∠B=,在△ABC中,根据三角形内角和定理可得关于x的方程,解方程即可求解.
45.
解:由题意,得:圆锥的侧面积为;
故答案为:.
根据圆锥的侧面积公式计算即可求解.
46.12
解:设红球有x个,由题意可得,
,
解得:,
经检验:是方程的解,
故答案为:12.
设红球有x个,根据频率=红球个数÷总数可得关于x的方程,解方程即可求解.
47.
48.132
49.22
50.
同课章节目录
