专项2 填空题2 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项2 填空题2 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 684.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项2 填空题2 (浙江中考真题+中考模拟)
一、填空题
1.(2024·浙江)有甲、乙两只大小不同的水箱,容量分别为升、升,且已各装有一些水,若将甲水箱中的水全倒入乙水箱,乙水箱只可再装升的水;若将乙水箱中的水倒入甲水箱,装满甲水箱后,乙水箱还剩升的水.则与之间的数量关系是 .
2.(2024·浙江)关于x的一元一次不等式组的解为,则m的取值范围为 .
3.(2024·金华真题)若平面直角坐标系内的点满足横、纵坐标都为整数,则把这样的点叫做"整点".例如:都是"整点".抛物线与轴交于点M、N两点,若该抛物线在M、N之间的部分与线段MN'所围成的区域(包括边界)恰有七个整点,则t的取值范围是 。
4.(2024·金华真题),点是边AB上的动点,以PC为边,在AC上方构造等边三角形,连接BQ.则面积的最大值是 .
5.(2025·湖州模拟)如图,在平行四边形中,是点B关于对角线的对称点,连结交于点E,连结交于点F,交于点G.,,则的面积是 .
6.(2025·湖州模拟)如图,A是函数的图象上一点,过点A作轴,交函数的图象于点B,点C在x轴上,若的面积是2,则k的值是 .
7.(2025·湖州模拟)关于x的方程有实数根,则m的取值范围是 .
8.(2025·湖州模拟)一个布袋里装有7个红球,2个黑球,1个白球,它们除颜色外其余都相同,从袋中随机摸出的一个球是黑球的概率为 .
9.(2025九下·南山模拟)因式分解:x2-4x= 。
10.(2025·浙江模拟) 如图,把一张矩形纸片ABCD沿 BE折叠,点A 的对应点为F,EF交 BD于点 G.若点 G为EF的中点,BF平分∠DBC,则= .
11.(2025·浙江模拟) 如图,已知AD//BC,BD⊥AC,AC=4,BD=8,则 sin∠DBC= .
12.(2025·浙江模拟)若一元二次方程x2-2x+k=0有两个相等的实数根,则k= .
13.(2025·浙江模拟) 如图,AB与⊙O相切于点A,连接OB与⊙O交于点C,连接AC.若AC=AO,则∠B= °.
14.(2025·浙江模拟)作为一个悠久历史和灿烂文化的文明古国,中国古代数学家曾写下不少数学著作,现从《九章算术》、《周髀算经》、《孙子算经》、《海岛算经》、《缉古算经》5本著作中随机挑选一本来研读,恰好选择《九章算术》的概率是 .
15.(2025·浙江模拟)因式分解:x2-4=
16.(2025九下·浙江模拟) 如图,△ABC中,∠ACB=90°,BC=1,AC=2,以斜边AB为边,向上作等边三角形ABD,则CD的长为 .
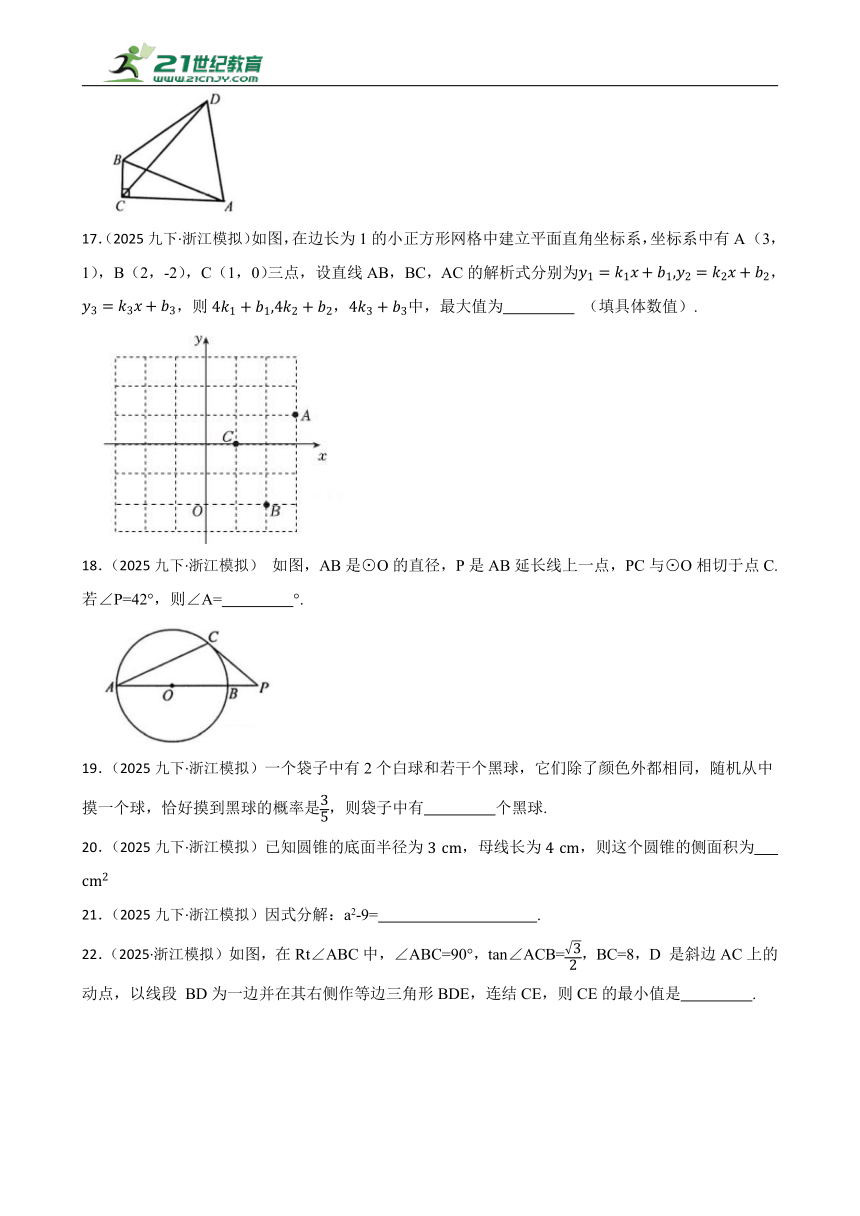
17.(2025九下·浙江模拟)如图,在边长为1的小正方形网格中建立平面直角坐标系,坐标系中有A (3, 1), B (2, -2), C (1, 0)三点, 设直线AB, BC, AC的解析式分别为,,则,中,最大值为 (填具体数值).
18.(2025九下·浙江模拟) 如图,AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C.若∠P=42°,则∠A= °.
19.(2025九下·浙江模拟)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 个黑球.
20.(2025九下·浙江模拟)已知圆锥的底面半径为,母线长为,则这个圆锥的侧面积为
21.(2025九下·浙江模拟)因式分解:a2-9= .
22.(2025·浙江模拟)如图,在Rt∠ABC中,∠ABC=90°,tan∠ACB=,BC=8,D 是斜边AC上的动点,以线段 BD为一边并在其右侧作等边三角形BDE,连结CE,则CE的最小值是 .
23.(2025·浙江模拟)如图,在四边形ABCD中,AD//BC,∠ABC=90°,点E在AB的延长线上,DE分别交BC,AC于点F,G.若AB=5,AE=AD=8,EF=DG,则BC= .
24.(2025·浙江模拟)如图,扇形OAB的半径为cm,且∠AOB=45°,则它的面积为 cm2.
25.(2025·浙江模拟) 当x= 时,分式的值为0.
26.(2025·浙江模拟)因式分解:x2-x= .
27.(2024九下·湖州模拟)已知圆的半径为,则的圆心角所对的弧的长是 cm. (结果保留根号)
28.(2024·余姚模拟)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
29.(2024九下·玉环模拟)分解因式:a2+2a= .
30.(2024九下·乐清模拟)如图,O为斜边AB上一点,以为半径的交边于点D,恰好为的切线,若,则 度.
31.(2024九下·乐清模拟)计算: .
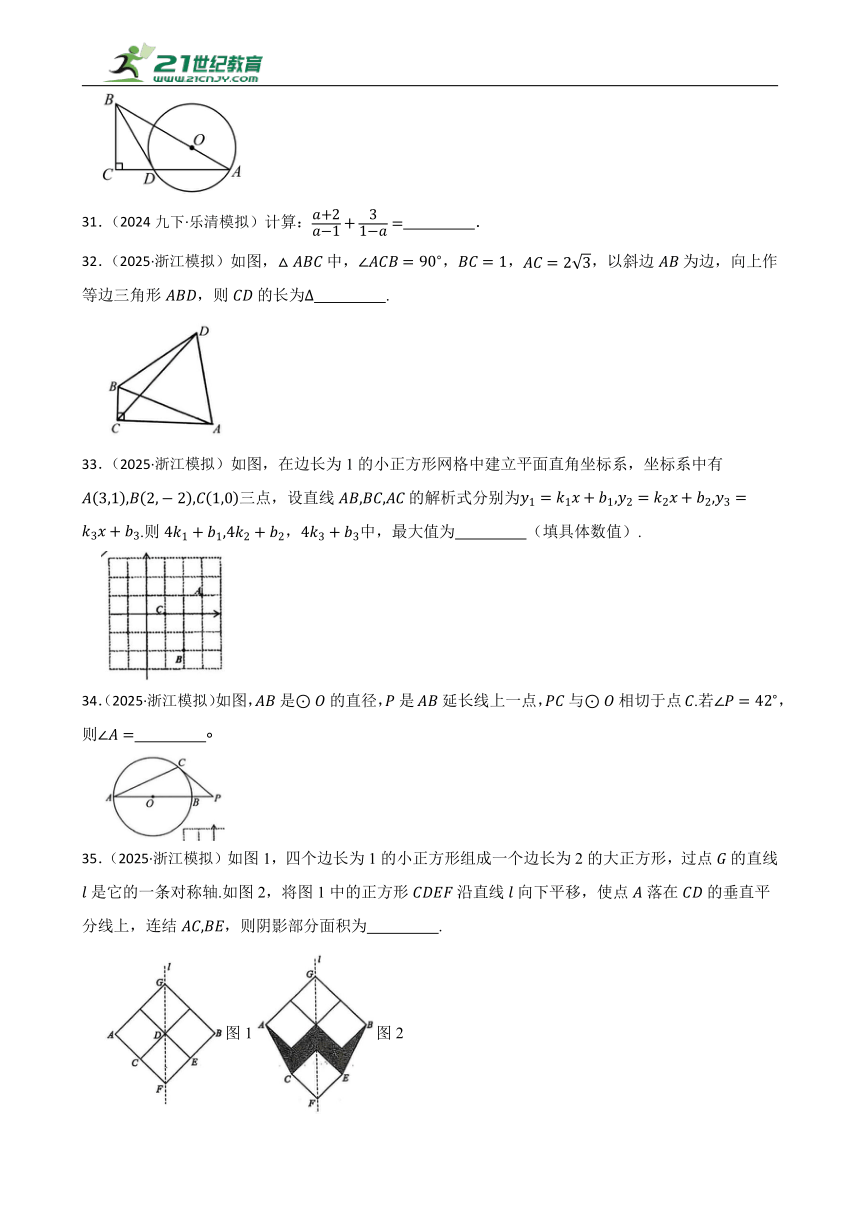
32.(2025·浙江模拟)如图,中,,,,以斜边为边,向上作等边三角形,则的长为 .
33.(2025·浙江模拟)如图,在边长为1的小正方形网格中建立平面直角坐标系,坐标系中有三点,设直线的解析式分别为.则,中,最大值为 (填具体数值).
34.(2025·浙江模拟)如图,是的直径,是延长线上一点,与相切于点.若,则
35.(2025·浙江模拟)如图1,四个边长为1的小正方形组成一个边长为2的大正方形,过点的直线是它的一条对称轴.如图2,将图1中的正方形沿直线向下平移,使点落在的垂直平分线上,连结,则阴影部分面积为 .
图1图2
36.(2025·浙江模拟)如图,,点在边上,,分别交于点,.若,则 (用含的式子表示).
37.(2025·浙江模拟)已知,代数式的值为 .
38.(2025·浙江模拟)现有一组数据:5,6,6,7,9,9,方差为;去掉数字7得到一组新的数据,方差为;则 (填“>”,“=”或“”).
39.(2025·浙江模拟)正十边形的一个外角的度数为 。
40.(2025·浙江模拟)若分式有意义,则应满足 .
41.(2025·浙江模拟)如图,在菱形ABCD中,,点为AB中点,将菱形沿FG折叠,使点与点重合,连结EF,~EG,则 .
42.(2025·浙江模拟)如图,在中,AD是BC上的中线,交AD于点.若,,则AB的长为 .
43.(2025·浙江模拟)如图,直线AB与的相切于点C,AO交于点,连结CD,OC.若,则的度数是 .
44.(2025·浙江模拟)若分式的值为2,则 .
45.(2025·浙江模拟)一个袋子中有5个红球和4个黑球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到黑球的概率是 .
46.(2025·汇川模拟)因式分解: .
47.(2025·浙江模拟)因式分解: = .
48.(2025九下·洞头模拟)有3张卡片,上面分别写着数1,2,3,从中随机抽取2张,数字之和是偶数的概率是 .
49.(2025九下·洞头模拟)若,则 .
50.(2024·中山模拟)分解因式: .
答案解析部分
1.
2.
3.
4.
解:如图,延长BA到E,使AE=AC,连QE,过Q作QF⊥AE交AE于点F,
∵∠BAC=120°,
∴∠CAE=60°,
∴△ACE为等边三角形,
∴CE=AC,∠CAE=∠CEA=∠ECA=60°,
∵△PCQ为等边三角形,
∴∠PCQ=∠ACE=60°,CP=CQ,
∴∠PCA=∠QCE,
∴△ACP≌△ECQ(SAS),
∴∠PAC=∠QEC=120°,PA=QE,
∴∠QEF=∠QEC-∠AEC=120°-60°=60°,
∴∠FQE=90°-60°=30°,
∴,
∴,
∵AB=AC=18,
∴BP=AB-PA=18-QE,
∴
∵,
∴当QE=9时,S△BPQ有最大值,最大值为.
故答案为:.
如图,延长BA到E,使AE=AC,连QE,过Q作OF⊥AE交AE于点F,证出
△ACP≌△ECO(SAS)得出∠FOE=30°,然后利用勾股定理得出,用含QE的式子表示出△BPO面积,最后利用二次函数的性质即可得解.
5.
6.3
7.
8.
9.x(x-4)
解:x2-4x= x(x-4);
故答案为:x(x-4).
提取公因式x, 分解因式即可。
10.
解:延长EF交BC于点H,设EG=y,DG=x,
根据折叠的性质,可得AB=BF,∠A=∠BFG=90°=∠BFH,AE=EF,
∵BF平分∠DBC,
∴∠FBG=∠FBH=∠DBC,
在△BFG与△BFH中,
∴△BFG≌△BFH(ASA),
∴FG=FH,
∵G为EF的中点,
∴GE=GF,
∴GF=FH=y,
∴AE=EF=2y,
∵四边形ABCD是矩形,
∴AD//BC,AD=BC,
∴EG:GH=DG:BG=DE:BH,
∴y:(y+y)=x:BG,解得BG=2x,
∴BH=BG=2x,
∴DE:2x=y:2y,解得DE=x.
∴AD=AE+DE=2y+x=BC.
∴,
,
∵AB=BF,
∴AB2=BF2,
∴,解得y=-2x(舍去)或3y=2x.
∴.
∴.
∴.
故答案为:.
设EG=y,DG=x,先利用ASA证明△BFG≌△BFH,再根据矩形的性质,得出AD//BC,AD=BC,根据平行线截的线段成比例,列出比例式求出BG=2x,再利用勾股定理,分别求出AB2,BF2,根据AB2=BF2,求出x与y的关系,再求出.
11.
解:过点D作DE//AC,交BC延长线于点E,
∵AD//BC,
∴四边形ADEC是平行四边形,
∴AC=DE=4,
∵DB⊥AC,
∴BD⊥DE.
∴∠BDE=90°.
∴BE===4.
∴sin∠DBC=.
故答案为:.
先证明四边形ADEC是平行四边形,根据平行四边形的性质可得AC=DE=4,再证明∠BDE=90°,利用勾股定理求得BE,再求得sin∠DBC.
12.1
解:∵一元二次方程x2-2x+k=0有两个相等的实数根,
∴(-2)2-4×1×k=0,解得k=1
故答案为:1.
根据一元二次方程有两个相等的实数根,计算判别式,得到关于k的方程求解.
13.30
解:∵AC=AO,OA=OC,
∴△OAC是等边三角形,
∴∠AOC=60°,
∵AB与⊙O相切于点A,
∴∠OAB=90°,
∴∠B=180°-∠OAB-∠AOB=180°-90°-60°=30°.
故答案为:30.
先证明△OAC是等边三角形,再根据切线的性质与三角形内角和定理求得 ∠B .
14.
解:从5本著作中随机挑选一本来研读,恰好选择《九章算术》的概率是.
故答案为:.
根据概率公式直接求解.
15.(x+2)(x-2)
解:x2-4=(x+2)(x-2).
故答案为:(x+2)(x-2).
直接利用平方差公式法分解即可。
16.
解:过点D作DH⊥AC于点H,DG⊥BC交CB延长线于点G,设CH=x,
∴∠G=90°,∠DHC=90°,
∵∠ACB=90°,
∴四边形CHDG是矩形,
∵BC=1,AC=2,
∴AB=.
∴AH=2-r,GD=CH=r,
∴DH2=AD2-AH2=13-(2-r)2,
∴BG2=BD2-DG2=13-r2,
∵GB+BC=GC=DH,
∴,
∴r2-2r+=0,
,
解得r1=,r2=.
当r=时,CD=.
当r=时,CD=.
在△BCD中, ∠CBD>90°,
∴CD>BD=,
∴CD=不符合题意.
故答案为:.
过点D作DH⊥AC于点H,DG⊥BC交CB延长线于点G,设CH=x,可证明四边形CHDG是矩形,利用勾股定理可求得AB,接着用r表示出AH,DG,然后利用GB+BC=GC=DH,得到关于r的方程,求出r,再求出CD的值.
17.4
解:∵ A (3, 1), B (2, -2), 直线AB的解析式为,
∴,解得.
∵ B (2, -2), C (1, 0),直线BC的解析式为,
∴,解得.
∵ A (3, 1), C (1, 0),直线AC的解析式为,
∴,解得.
∴,,,
∴,,中最大值为4.
故答案为:4.
先分别求出三直线的解析式,再求出,的值,然后写了最大值.
18.24
解:连结OC,
∵ PC与⊙O相切于点C
∴OC⊥CP,
∴∠P+ ∠COP=90 ° ,
∵ ∠P=42°,
∴42°+ ∠COP=90 ° ,解得∠COP=48° ,
又∠COP是△ACO的一个外角,OC=OA,
∴∠COP=∠A+∠ACO=2∠A,
∴2∠A=48° ,解得∠A=24°.
故答案为:24.
先利用切线的意义,说明OC⊥CP,再利用直角三角形的两个锐角互余,求出∠COP,再利用三角形外角的性质求出∠A.
19.3
解:设袋子中有x个黑球,
根据题意,得,
解得:x=3,
经检验x=3是分数方程的解,
∴袋子中有3个黑球,
故答案为:3.
设袋子中有x个黑球,根据概率公式得关于x的分式方程,解方程即可求解.
20.
解:∵圆锥的底面半径为3cm,母线长为4cm,
∴这个圆锥的侧面积为,
故答案为:.
根据圆锥侧面积公式(r是圆锥底面圆半径,l是圆锥母线长)直接求解即可.
21.(a+3)(a﹣3)
解:a2-9=(a+3)(a-3)。
故答案为: (a+3)(a﹣3) 。
利用平方差公式分解即可。
22.
解:∵在Rt△ABC中,∠ABC=90°,
∴tan∠ACB=.
∵tan∠ACB=,BC=8,
∴=,解得AB=4.
∴AC=.
以BC为边在BC上方作等边△BCF,连接DF,AF,过点F作FG⊥BC于点G,
∵△BDE是等边三角形,
∴BD=BE,BC=BF=8, ∠DBE=∠FBC=60°,
∴∠DBE-∠FBE=∠FBC-∠FBE,
∴∠DBF=∠EBC,
∴△DBF≌△EBC(SAS),
∴CE=DF,
当DF⊥AC时,DF的值最小,CE的值就最小,
∵BG=BC=4,“
∴FG==4,
∴FG=AB,
∵FG//AB,
∴四边形ABGF是平行四边形,
∵∠ABC=90°,
∴四边形ABGF是矩形,
∴AF//BC,AF =BG=4,
∴∠FAC=∠ACB,
∵∠ADF=∠ABC=90°,
∴△ADF∽△CBA,
∴DF:AB=AF:AC,
∴DF:4=4:4,解得DF=.
∴CE的最小值为.
故答案为:.
先利用正切求出AB,再利用勾股定理求出AC,以BC为边在BC上方作等边△BCF,连接DF,AF,过点F作FG⊥BC于点G,利用SAS证明△DBF≌△EBC,根据全等三角形的性质可得CE=DF,当DF⊥AC时,DF的值最小,CE的值就最小,利用勾股定理求得FG,再证明四边形ABGF是矩形,根据矩形的性质,可证明△ADF∽△CBA,列出关于DF的比例式,求出DF,即为CE的最小值.
23.
解:∵AB=5,AE=AD=8,
∴BE=AE-AB=3,
∵AD//BC,∠ABC=90°,
∴∠DAE=∠FBE=90°,
∴DE=.
∴∠ADE=∠AED =(180°-∠DAE)=45°,
∴∠BFE=∠ADE=45°,
∴BF=BE=3,
∴EF=.
∴DG=EF=3.
∴FG=DE-DG-EF=2.
∵AD//BC,
∴△ADG∽△CFG.
∴CF:AD=FG:DG,
∴CF:8=2:3,解得CF=.
∴BC=BF+CF=3+=.
故答案为:.
先利用线段差求出BE,再利用勾股定理求得DE,EF,然后求出FG,再证明△ADG∽△CFG,列出关于CF的比例式,求出CF,再根据BC=BF+CF,求出BC.
24.
解:∵ 扇形OAB的半径为cm,且∠AOB=45°,
∴扇形AOB的面积为(cm2).
故答案为:.
直接利用扇形面积公式求解.
25.3
解:∵分式的值为0,
∴x-3=0且x-1≠0,解得x=3.
故答案为:3.
根据分式的值为0,列出方程求解.
26.x(x-1)
解:x2-x=x(x-1)
答案为:x(x-1)
观察此多项式含有公因式,提取公因式即可。
27.
解:由题意知,,∴(cm),
故答案为:.
此题主要考查了扇形的弧长公式。直接利用扇形的弧长公式,将公式列出之后代入相关数据计算即可得出结论.
28.3
解:根据题意可知:球的总个数为:,
∴n=9-6=3.
故答案为:3.
根据红球的个数以及任意摸出一个球是红球的概率为可以求得球的总个数,进而即可得到答案。
29.a(a+2)
解:a2+2a=a(a+2).
故答案为:a(a+2).
直接提取公因式a,进而得出答案.
30.31
解:连接,
∵恰好为的切线,
∴,
∵
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:31.
有切线,连半径是解决圆的计算与证明的常用策略,因此连接OD,则得到直角三角形ODB,利用内角和定理可知度数,再利用外角的性质可知度数,再利用外角的性质可知度数,最后利用直角三角形两锐角互余即可.
31.1
解:原式
,
故答案为:1.
由于分母是一对相反数,直接应用同分母分式的减法运算法则即可.
32.
解:如图,以AC为边向下作等边,过点E作EF⊥BC,交BC延长线于F,连接CE,BE,
∴AC=AE=CE,∠CAE=∠ACE=60°,∠F=90°,
∵是等边三角形,
∴AD=AB,∠BAD=60°,
∴∠BAD+∠BAC=∠BAC+∠CAE,
∴∠DAC=∠BAE,
在和中,
,
∴,
∴CD=BE,
∵∠ACB=90°,∠ACE=60°,
∴∠ECF=180°-90°-60°=30°,
∵,
∴,
∴,
∴,
∵BC=1,
∴BF=BC+CF=1+3=4,
∴,
故答案为:.
以AC为边向下作等边,过点E作EF⊥BC,交BC延长线于F,连接CE,BE,根据等边三角形的性质,利用“手拉手全等”模型证明,得CD=BE,然后求出∠ECF=30°,根据含30°的直角三角形的性质得,从而利用勾股定理求出CF=3,进而得BF=4,最后再利用勾股定理求出BE的值.
33.4
解:将A(3,1),B(2,-2)代入,得,
解得:,
∴,
将B(2,-2),C(1,0)代入,得,
解得:,
∴,
将A(3,1),C(1,0)代入,得,
解得:,
∴,
∴,中,最大值为4,
故答案为:4.
将A,B,C的坐标分别代入三个解析式中求出的值,再求出,的值进行比较即可.
34.24
解:如图,连接OC,
∵PC与相切于点C,
∴OC⊥PC,
∴∠PCO=90°,
∵∠P=42°,
∴∠COP=90°-∠P=90°-42°=48°,
∵OA=OC,
∴∠A=∠ACO,
∵∠COP=∠A+∠ACO,
∴∠A=24°,
故答案为:24.
连接OC,根据切线的性质得∠PCO=90°,从而得∠COP=48°,根据等腰三角形“等边对等角”性质得∠A=∠ACO,再根据三角形外角性质求解即可.
35.
解:如图, 连接MC, 延长AM交CD于点N,
∵点A落在CD的垂直平分线上,
由平移,得
故答案为:
连接MC,延长AM交CD于点N,根据垂直平分线的性质得到由平移的性质得到 求出 即可解答.
36.
解:设AB=a,则AC=ma,
∵△ABC≌△DAC,
∴AD=AB=a,
∴DC=AC-AD=ma-a,
又∵∠BAC=∠ADE=90°,
∴∠BAC+∠ADE=180°,
∴DE∥AB,
∴CG:BG=CD:AD=(ma-a):a=m-1,
故答案为:m-1.
设AB=a,则AC=ma,根据全等得到AD=AB=a,然后得到DE∥AB,即可得到CG:BG=CD:AD解题即可.
37.9
解:
则原式
故答案为:9.
原式利用完全平方公式,多项式乘多项式法则计算,去括号合并得到最简结果,把已知等式代入计算即可求出值.
38.
解:
;去掉数字7后,
,
.
故答案为:<.
先根据方差公式计算 和 的值,然后比较解题.
39.36
解:
故答案为:36.
根据多边形的外角和是360°解题即可.
40.
解:解:∵ 分式有意义,
∴,
解得,
故答案为:.
根据分式有意义的条件为分母不为零解题即可.
41.1.2
解:如图,过点G作GH垂直AB的延长线于点H,则∠GHB=90°,
∵四边形ABCD是菱形,且AB=4,
∴AD∥BC,BC=AB=4,
设BG=x,
由折叠性质可得EG=CG=4-x,
∵点E是AB的中点,
∴BE=,
∵AD∥BC,∠A=60°,
∴∠CBH=∠A=60°,
∴∠BGH=90°-∠CBH=30°,
∴BH=BG=x,HG=x,
∴EH=EB+BH=2+x,
在Rt△HGE中,∵EH2+HG2=EG2,
∴
解得x=1.2,即BG=1.2.
故答案为:1.2.
如图,过点G作GH垂直AB的延长线于点H,则∠GHB=90°,由菱形的性质得AD∥BC,BC=AB=4,设BG=x,由折叠性质可得EG=CG=4-x,由二直线平行,同位角相等得∠CBH=∠A=60°,根据三角形内角和定理求出∠BGH=30°,由含30°角直角三角形的性质可用含x的式子表示出BH、HG的长,在Rt△HGE中,利用勾股定理建立方程可求出x的值,从而得出答案.
42.
解:取BE的中点G,连接DG,如图,则BE=2GE,
∵AD是BC上的中线,
∴点D是BC的中点,
∴GD是△BCE的中位线,
∴GD∥AC,GD=CE=1,
∴∠EAF=∠FDG,∠AEF=∠DGF,
又AF=DF,
∴△AEF≌△DGF(AAS),
∴GF=EF=,AE=GD=1,
∴GE=EF+GF=,
∴BE=2GE=3,
∵BE⊥AC,
∴∠AEB=90°,
在Rt△AEB中,.
故答案为:.
取BE的中点G,连接DG,如图,则BE=2GE,由三角形的中位线定理得GD∥AC,GD=CE=1,由二直线平行,内错角相等,得∠EAF=∠FDG,∠AEF=∠DGF,从而由AAS判断出△AEF≌△DGF,根据全等三角形的对应边相等得GF=EF=,AE=GD=1,则可得BE=2GE=3,最后在Rt△AEB中,利用勾股定理可算出AB的长.
43.64°
解:∵直线AB与的相切于点,
∴∠ACO=90°,
又∵∠ACD=32°,
∴∠OCD=∠ACO-∠ACD=58°,
∵OC=OD,
∴∠OCD=∠ODC=58°,
∴∠COD=180°-∠OCD-∠ODC=64°.
故答案为:64°.
由圆的切线垂直于经过切点的半径可得∠ACO=90°,然后根据角的构成可算出∠OCD=∠ACO-∠ACD=58°,由等边对等角得∠OCD=∠ODC=58°,最后根据三角形的内角和定理可算出∠COD的度数.
44.9
解:由题意得,
去分母得1+x=2x-8,
移项、合并同类项,得x=9,
经检验,x=9是原分式方程的根.
故答案为:9.
由分式的值为2可列出关于字母x的分式方程,方程两边同时乘以x-4约去分母将分式方程转化为整式方程,解整式方程求出x的值,再检验即可得出答案.
45.
解:由题意可得: 随机从中摸一个球,恰好摸到黑球的概率是.
故答案为:.
根据概率公式,用袋中黑色小球的个数比上袋中小球的总个数即可得出随机从中摸一个球,恰好摸到黑球的概率.
46.
a2-9=(a+3)(a-3)。
故答案为:(a+3)(a-3)。
由平方差公式:a2-b2=(a+b)(a-b)可得。
47.
解:a2﹣3a=a(a﹣3).故答案为:a(a﹣3).
根据提取公因式法进行因式分解即可。
48.
解:列表如下:
1 2 3
1 — 3 4
2 3 — 5
3 4 5 —
由上表可知,共有6种等可能得结果,其中偶数有2种,
数字之和是偶数的概率是,
故答案为:.
本题考查列表法求概率.先列表求出从中随机抽取2张,数字之和的全部结果数,再数出偶数结果数,再利用简单概率公式进行计算可求出概率.
49.1
解:,
去分母得,,
移项、合并同类项得,
解得.
检验:把代入,
是原分式方程的解.
故答案为:.
本题考查分式方程的解法.先去分母化成一元一次方程,移项、合并同类项得,再将x的系数化为1可求出x的值,再进行检验可求出方程的解.
50.
解:,
故答案为:.
利用提公因式法因式分解即可.
专项2 填空题2 (浙江中考真题+中考模拟)
一、填空题
1.(2024·浙江)有甲、乙两只大小不同的水箱,容量分别为升、升,且已各装有一些水,若将甲水箱中的水全倒入乙水箱,乙水箱只可再装升的水;若将乙水箱中的水倒入甲水箱,装满甲水箱后,乙水箱还剩升的水.则与之间的数量关系是 .
2.(2024·浙江)关于x的一元一次不等式组的解为,则m的取值范围为 .
3.(2024·金华真题)若平面直角坐标系内的点满足横、纵坐标都为整数,则把这样的点叫做"整点".例如:都是"整点".抛物线与轴交于点M、N两点,若该抛物线在M、N之间的部分与线段MN'所围成的区域(包括边界)恰有七个整点,则t的取值范围是 。
4.(2024·金华真题),点是边AB上的动点,以PC为边,在AC上方构造等边三角形,连接BQ.则面积的最大值是 .
5.(2025·湖州模拟)如图,在平行四边形中,是点B关于对角线的对称点,连结交于点E,连结交于点F,交于点G.,,则的面积是 .
6.(2025·湖州模拟)如图,A是函数的图象上一点,过点A作轴,交函数的图象于点B,点C在x轴上,若的面积是2,则k的值是 .
7.(2025·湖州模拟)关于x的方程有实数根,则m的取值范围是 .
8.(2025·湖州模拟)一个布袋里装有7个红球,2个黑球,1个白球,它们除颜色外其余都相同,从袋中随机摸出的一个球是黑球的概率为 .
9.(2025九下·南山模拟)因式分解:x2-4x= 。
10.(2025·浙江模拟) 如图,把一张矩形纸片ABCD沿 BE折叠,点A 的对应点为F,EF交 BD于点 G.若点 G为EF的中点,BF平分∠DBC,则= .
11.(2025·浙江模拟) 如图,已知AD//BC,BD⊥AC,AC=4,BD=8,则 sin∠DBC= .
12.(2025·浙江模拟)若一元二次方程x2-2x+k=0有两个相等的实数根,则k= .
13.(2025·浙江模拟) 如图,AB与⊙O相切于点A,连接OB与⊙O交于点C,连接AC.若AC=AO,则∠B= °.
14.(2025·浙江模拟)作为一个悠久历史和灿烂文化的文明古国,中国古代数学家曾写下不少数学著作,现从《九章算术》、《周髀算经》、《孙子算经》、《海岛算经》、《缉古算经》5本著作中随机挑选一本来研读,恰好选择《九章算术》的概率是 .
15.(2025·浙江模拟)因式分解:x2-4=
16.(2025九下·浙江模拟) 如图,△ABC中,∠ACB=90°,BC=1,AC=2,以斜边AB为边,向上作等边三角形ABD,则CD的长为 .
17.(2025九下·浙江模拟)如图,在边长为1的小正方形网格中建立平面直角坐标系,坐标系中有A (3, 1), B (2, -2), C (1, 0)三点, 设直线AB, BC, AC的解析式分别为,,则,中,最大值为 (填具体数值).
18.(2025九下·浙江模拟) 如图,AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C.若∠P=42°,则∠A= °.
19.(2025九下·浙江模拟)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 个黑球.
20.(2025九下·浙江模拟)已知圆锥的底面半径为,母线长为,则这个圆锥的侧面积为
21.(2025九下·浙江模拟)因式分解:a2-9= .
22.(2025·浙江模拟)如图,在Rt∠ABC中,∠ABC=90°,tan∠ACB=,BC=8,D 是斜边AC上的动点,以线段 BD为一边并在其右侧作等边三角形BDE,连结CE,则CE的最小值是 .
23.(2025·浙江模拟)如图,在四边形ABCD中,AD//BC,∠ABC=90°,点E在AB的延长线上,DE分别交BC,AC于点F,G.若AB=5,AE=AD=8,EF=DG,则BC= .
24.(2025·浙江模拟)如图,扇形OAB的半径为cm,且∠AOB=45°,则它的面积为 cm2.
25.(2025·浙江模拟) 当x= 时,分式的值为0.
26.(2025·浙江模拟)因式分解:x2-x= .
27.(2024九下·湖州模拟)已知圆的半径为,则的圆心角所对的弧的长是 cm. (结果保留根号)
28.(2024·余姚模拟)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
29.(2024九下·玉环模拟)分解因式:a2+2a= .
30.(2024九下·乐清模拟)如图,O为斜边AB上一点,以为半径的交边于点D,恰好为的切线,若,则 度.
31.(2024九下·乐清模拟)计算: .
32.(2025·浙江模拟)如图,中,,,,以斜边为边,向上作等边三角形,则的长为 .
33.(2025·浙江模拟)如图,在边长为1的小正方形网格中建立平面直角坐标系,坐标系中有三点,设直线的解析式分别为.则,中,最大值为 (填具体数值).
34.(2025·浙江模拟)如图,是的直径,是延长线上一点,与相切于点.若,则
35.(2025·浙江模拟)如图1,四个边长为1的小正方形组成一个边长为2的大正方形,过点的直线是它的一条对称轴.如图2,将图1中的正方形沿直线向下平移,使点落在的垂直平分线上,连结,则阴影部分面积为 .
图1图2
36.(2025·浙江模拟)如图,,点在边上,,分别交于点,.若,则 (用含的式子表示).
37.(2025·浙江模拟)已知,代数式的值为 .
38.(2025·浙江模拟)现有一组数据:5,6,6,7,9,9,方差为;去掉数字7得到一组新的数据,方差为;则 (填“>”,“=”或“”).
39.(2025·浙江模拟)正十边形的一个外角的度数为 。
40.(2025·浙江模拟)若分式有意义,则应满足 .
41.(2025·浙江模拟)如图,在菱形ABCD中,,点为AB中点,将菱形沿FG折叠,使点与点重合,连结EF,~EG,则 .
42.(2025·浙江模拟)如图,在中,AD是BC上的中线,交AD于点.若,,则AB的长为 .
43.(2025·浙江模拟)如图,直线AB与的相切于点C,AO交于点,连结CD,OC.若,则的度数是 .
44.(2025·浙江模拟)若分式的值为2,则 .
45.(2025·浙江模拟)一个袋子中有5个红球和4个黑球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到黑球的概率是 .
46.(2025·汇川模拟)因式分解: .
47.(2025·浙江模拟)因式分解: = .
48.(2025九下·洞头模拟)有3张卡片,上面分别写着数1,2,3,从中随机抽取2张,数字之和是偶数的概率是 .
49.(2025九下·洞头模拟)若,则 .
50.(2024·中山模拟)分解因式: .
答案解析部分
1.
2.
3.
4.
解:如图,延长BA到E,使AE=AC,连QE,过Q作QF⊥AE交AE于点F,
∵∠BAC=120°,
∴∠CAE=60°,
∴△ACE为等边三角形,
∴CE=AC,∠CAE=∠CEA=∠ECA=60°,
∵△PCQ为等边三角形,
∴∠PCQ=∠ACE=60°,CP=CQ,
∴∠PCA=∠QCE,
∴△ACP≌△ECQ(SAS),
∴∠PAC=∠QEC=120°,PA=QE,
∴∠QEF=∠QEC-∠AEC=120°-60°=60°,
∴∠FQE=90°-60°=30°,
∴,
∴,
∵AB=AC=18,
∴BP=AB-PA=18-QE,
∴
∵,
∴当QE=9时,S△BPQ有最大值,最大值为.
故答案为:.
如图,延长BA到E,使AE=AC,连QE,过Q作OF⊥AE交AE于点F,证出
△ACP≌△ECO(SAS)得出∠FOE=30°,然后利用勾股定理得出,用含QE的式子表示出△BPO面积,最后利用二次函数的性质即可得解.
5.
6.3
7.
8.
9.x(x-4)
解:x2-4x= x(x-4);
故答案为:x(x-4).
提取公因式x, 分解因式即可。
10.
解:延长EF交BC于点H,设EG=y,DG=x,
根据折叠的性质,可得AB=BF,∠A=∠BFG=90°=∠BFH,AE=EF,
∵BF平分∠DBC,
∴∠FBG=∠FBH=∠DBC,
在△BFG与△BFH中,
∴△BFG≌△BFH(ASA),
∴FG=FH,
∵G为EF的中点,
∴GE=GF,
∴GF=FH=y,
∴AE=EF=2y,
∵四边形ABCD是矩形,
∴AD//BC,AD=BC,
∴EG:GH=DG:BG=DE:BH,
∴y:(y+y)=x:BG,解得BG=2x,
∴BH=BG=2x,
∴DE:2x=y:2y,解得DE=x.
∴AD=AE+DE=2y+x=BC.
∴,
,
∵AB=BF,
∴AB2=BF2,
∴,解得y=-2x(舍去)或3y=2x.
∴.
∴.
∴.
故答案为:.
设EG=y,DG=x,先利用ASA证明△BFG≌△BFH,再根据矩形的性质,得出AD//BC,AD=BC,根据平行线截的线段成比例,列出比例式求出BG=2x,再利用勾股定理,分别求出AB2,BF2,根据AB2=BF2,求出x与y的关系,再求出.
11.
解:过点D作DE//AC,交BC延长线于点E,
∵AD//BC,
∴四边形ADEC是平行四边形,
∴AC=DE=4,
∵DB⊥AC,
∴BD⊥DE.
∴∠BDE=90°.
∴BE===4.
∴sin∠DBC=.
故答案为:.
先证明四边形ADEC是平行四边形,根据平行四边形的性质可得AC=DE=4,再证明∠BDE=90°,利用勾股定理求得BE,再求得sin∠DBC.
12.1
解:∵一元二次方程x2-2x+k=0有两个相等的实数根,
∴(-2)2-4×1×k=0,解得k=1
故答案为:1.
根据一元二次方程有两个相等的实数根,计算判别式,得到关于k的方程求解.
13.30
解:∵AC=AO,OA=OC,
∴△OAC是等边三角形,
∴∠AOC=60°,
∵AB与⊙O相切于点A,
∴∠OAB=90°,
∴∠B=180°-∠OAB-∠AOB=180°-90°-60°=30°.
故答案为:30.
先证明△OAC是等边三角形,再根据切线的性质与三角形内角和定理求得 ∠B .
14.
解:从5本著作中随机挑选一本来研读,恰好选择《九章算术》的概率是.
故答案为:.
根据概率公式直接求解.
15.(x+2)(x-2)
解:x2-4=(x+2)(x-2).
故答案为:(x+2)(x-2).
直接利用平方差公式法分解即可。
16.
解:过点D作DH⊥AC于点H,DG⊥BC交CB延长线于点G,设CH=x,
∴∠G=90°,∠DHC=90°,
∵∠ACB=90°,
∴四边形CHDG是矩形,
∵BC=1,AC=2,
∴AB=.
∴AH=2-r,GD=CH=r,
∴DH2=AD2-AH2=13-(2-r)2,
∴BG2=BD2-DG2=13-r2,
∵GB+BC=GC=DH,
∴,
∴r2-2r+=0,
,
解得r1=,r2=.
当r=时,CD=.
当r=时,CD=.
在△BCD中, ∠CBD>90°,
∴CD>BD=,
∴CD=不符合题意.
故答案为:.
过点D作DH⊥AC于点H,DG⊥BC交CB延长线于点G,设CH=x,可证明四边形CHDG是矩形,利用勾股定理可求得AB,接着用r表示出AH,DG,然后利用GB+BC=GC=DH,得到关于r的方程,求出r,再求出CD的值.
17.4
解:∵ A (3, 1), B (2, -2), 直线AB的解析式为,
∴,解得.
∵ B (2, -2), C (1, 0),直线BC的解析式为,
∴,解得.
∵ A (3, 1), C (1, 0),直线AC的解析式为,
∴,解得.
∴,,,
∴,,中最大值为4.
故答案为:4.
先分别求出三直线的解析式,再求出,的值,然后写了最大值.
18.24
解:连结OC,
∵ PC与⊙O相切于点C
∴OC⊥CP,
∴∠P+ ∠COP=90 ° ,
∵ ∠P=42°,
∴42°+ ∠COP=90 ° ,解得∠COP=48° ,
又∠COP是△ACO的一个外角,OC=OA,
∴∠COP=∠A+∠ACO=2∠A,
∴2∠A=48° ,解得∠A=24°.
故答案为:24.
先利用切线的意义,说明OC⊥CP,再利用直角三角形的两个锐角互余,求出∠COP,再利用三角形外角的性质求出∠A.
19.3
解:设袋子中有x个黑球,
根据题意,得,
解得:x=3,
经检验x=3是分数方程的解,
∴袋子中有3个黑球,
故答案为:3.
设袋子中有x个黑球,根据概率公式得关于x的分式方程,解方程即可求解.
20.
解:∵圆锥的底面半径为3cm,母线长为4cm,
∴这个圆锥的侧面积为,
故答案为:.
根据圆锥侧面积公式(r是圆锥底面圆半径,l是圆锥母线长)直接求解即可.
21.(a+3)(a﹣3)
解:a2-9=(a+3)(a-3)。
故答案为: (a+3)(a﹣3) 。
利用平方差公式分解即可。
22.
解:∵在Rt△ABC中,∠ABC=90°,
∴tan∠ACB=.
∵tan∠ACB=,BC=8,
∴=,解得AB=4.
∴AC=.
以BC为边在BC上方作等边△BCF,连接DF,AF,过点F作FG⊥BC于点G,
∵△BDE是等边三角形,
∴BD=BE,BC=BF=8, ∠DBE=∠FBC=60°,
∴∠DBE-∠FBE=∠FBC-∠FBE,
∴∠DBF=∠EBC,
∴△DBF≌△EBC(SAS),
∴CE=DF,
当DF⊥AC时,DF的值最小,CE的值就最小,
∵BG=BC=4,“
∴FG==4,
∴FG=AB,
∵FG//AB,
∴四边形ABGF是平行四边形,
∵∠ABC=90°,
∴四边形ABGF是矩形,
∴AF//BC,AF =BG=4,
∴∠FAC=∠ACB,
∵∠ADF=∠ABC=90°,
∴△ADF∽△CBA,
∴DF:AB=AF:AC,
∴DF:4=4:4,解得DF=.
∴CE的最小值为.
故答案为:.
先利用正切求出AB,再利用勾股定理求出AC,以BC为边在BC上方作等边△BCF,连接DF,AF,过点F作FG⊥BC于点G,利用SAS证明△DBF≌△EBC,根据全等三角形的性质可得CE=DF,当DF⊥AC时,DF的值最小,CE的值就最小,利用勾股定理求得FG,再证明四边形ABGF是矩形,根据矩形的性质,可证明△ADF∽△CBA,列出关于DF的比例式,求出DF,即为CE的最小值.
23.
解:∵AB=5,AE=AD=8,
∴BE=AE-AB=3,
∵AD//BC,∠ABC=90°,
∴∠DAE=∠FBE=90°,
∴DE=.
∴∠ADE=∠AED =(180°-∠DAE)=45°,
∴∠BFE=∠ADE=45°,
∴BF=BE=3,
∴EF=.
∴DG=EF=3.
∴FG=DE-DG-EF=2.
∵AD//BC,
∴△ADG∽△CFG.
∴CF:AD=FG:DG,
∴CF:8=2:3,解得CF=.
∴BC=BF+CF=3+=.
故答案为:.
先利用线段差求出BE,再利用勾股定理求得DE,EF,然后求出FG,再证明△ADG∽△CFG,列出关于CF的比例式,求出CF,再根据BC=BF+CF,求出BC.
24.
解:∵ 扇形OAB的半径为cm,且∠AOB=45°,
∴扇形AOB的面积为(cm2).
故答案为:.
直接利用扇形面积公式求解.
25.3
解:∵分式的值为0,
∴x-3=0且x-1≠0,解得x=3.
故答案为:3.
根据分式的值为0,列出方程求解.
26.x(x-1)
解:x2-x=x(x-1)
答案为:x(x-1)
观察此多项式含有公因式,提取公因式即可。
27.
解:由题意知,,∴(cm),
故答案为:.
此题主要考查了扇形的弧长公式。直接利用扇形的弧长公式,将公式列出之后代入相关数据计算即可得出结论.
28.3
解:根据题意可知:球的总个数为:,
∴n=9-6=3.
故答案为:3.
根据红球的个数以及任意摸出一个球是红球的概率为可以求得球的总个数,进而即可得到答案。
29.a(a+2)
解:a2+2a=a(a+2).
故答案为:a(a+2).
直接提取公因式a,进而得出答案.
30.31
解:连接,
∵恰好为的切线,
∴,
∵
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:31.
有切线,连半径是解决圆的计算与证明的常用策略,因此连接OD,则得到直角三角形ODB,利用内角和定理可知度数,再利用外角的性质可知度数,再利用外角的性质可知度数,最后利用直角三角形两锐角互余即可.
31.1
解:原式
,
故答案为:1.
由于分母是一对相反数,直接应用同分母分式的减法运算法则即可.
32.
解:如图,以AC为边向下作等边,过点E作EF⊥BC,交BC延长线于F,连接CE,BE,
∴AC=AE=CE,∠CAE=∠ACE=60°,∠F=90°,
∵是等边三角形,
∴AD=AB,∠BAD=60°,
∴∠BAD+∠BAC=∠BAC+∠CAE,
∴∠DAC=∠BAE,
在和中,
,
∴,
∴CD=BE,
∵∠ACB=90°,∠ACE=60°,
∴∠ECF=180°-90°-60°=30°,
∵,
∴,
∴,
∴,
∵BC=1,
∴BF=BC+CF=1+3=4,
∴,
故答案为:.
以AC为边向下作等边,过点E作EF⊥BC,交BC延长线于F,连接CE,BE,根据等边三角形的性质,利用“手拉手全等”模型证明,得CD=BE,然后求出∠ECF=30°,根据含30°的直角三角形的性质得,从而利用勾股定理求出CF=3,进而得BF=4,最后再利用勾股定理求出BE的值.
33.4
解:将A(3,1),B(2,-2)代入,得,
解得:,
∴,
将B(2,-2),C(1,0)代入,得,
解得:,
∴,
将A(3,1),C(1,0)代入,得,
解得:,
∴,
∴,中,最大值为4,
故答案为:4.
将A,B,C的坐标分别代入三个解析式中求出的值,再求出,的值进行比较即可.
34.24
解:如图,连接OC,
∵PC与相切于点C,
∴OC⊥PC,
∴∠PCO=90°,
∵∠P=42°,
∴∠COP=90°-∠P=90°-42°=48°,
∵OA=OC,
∴∠A=∠ACO,
∵∠COP=∠A+∠ACO,
∴∠A=24°,
故答案为:24.
连接OC,根据切线的性质得∠PCO=90°,从而得∠COP=48°,根据等腰三角形“等边对等角”性质得∠A=∠ACO,再根据三角形外角性质求解即可.
35.
解:如图, 连接MC, 延长AM交CD于点N,
∵点A落在CD的垂直平分线上,
由平移,得
故答案为:
连接MC,延长AM交CD于点N,根据垂直平分线的性质得到由平移的性质得到 求出 即可解答.
36.
解:设AB=a,则AC=ma,
∵△ABC≌△DAC,
∴AD=AB=a,
∴DC=AC-AD=ma-a,
又∵∠BAC=∠ADE=90°,
∴∠BAC+∠ADE=180°,
∴DE∥AB,
∴CG:BG=CD:AD=(ma-a):a=m-1,
故答案为:m-1.
设AB=a,则AC=ma,根据全等得到AD=AB=a,然后得到DE∥AB,即可得到CG:BG=CD:AD解题即可.
37.9
解:
则原式
故答案为:9.
原式利用完全平方公式,多项式乘多项式法则计算,去括号合并得到最简结果,把已知等式代入计算即可求出值.
38.
解:
;去掉数字7后,
,
.
故答案为:<.
先根据方差公式计算 和 的值,然后比较解题.
39.36
解:
故答案为:36.
根据多边形的外角和是360°解题即可.
40.
解:解:∵ 分式有意义,
∴,
解得,
故答案为:.
根据分式有意义的条件为分母不为零解题即可.
41.1.2
解:如图,过点G作GH垂直AB的延长线于点H,则∠GHB=90°,
∵四边形ABCD是菱形,且AB=4,
∴AD∥BC,BC=AB=4,
设BG=x,
由折叠性质可得EG=CG=4-x,
∵点E是AB的中点,
∴BE=,
∵AD∥BC,∠A=60°,
∴∠CBH=∠A=60°,
∴∠BGH=90°-∠CBH=30°,
∴BH=BG=x,HG=x,
∴EH=EB+BH=2+x,
在Rt△HGE中,∵EH2+HG2=EG2,
∴
解得x=1.2,即BG=1.2.
故答案为:1.2.
如图,过点G作GH垂直AB的延长线于点H,则∠GHB=90°,由菱形的性质得AD∥BC,BC=AB=4,设BG=x,由折叠性质可得EG=CG=4-x,由二直线平行,同位角相等得∠CBH=∠A=60°,根据三角形内角和定理求出∠BGH=30°,由含30°角直角三角形的性质可用含x的式子表示出BH、HG的长,在Rt△HGE中,利用勾股定理建立方程可求出x的值,从而得出答案.
42.
解:取BE的中点G,连接DG,如图,则BE=2GE,
∵AD是BC上的中线,
∴点D是BC的中点,
∴GD是△BCE的中位线,
∴GD∥AC,GD=CE=1,
∴∠EAF=∠FDG,∠AEF=∠DGF,
又AF=DF,
∴△AEF≌△DGF(AAS),
∴GF=EF=,AE=GD=1,
∴GE=EF+GF=,
∴BE=2GE=3,
∵BE⊥AC,
∴∠AEB=90°,
在Rt△AEB中,.
故答案为:.
取BE的中点G,连接DG,如图,则BE=2GE,由三角形的中位线定理得GD∥AC,GD=CE=1,由二直线平行,内错角相等,得∠EAF=∠FDG,∠AEF=∠DGF,从而由AAS判断出△AEF≌△DGF,根据全等三角形的对应边相等得GF=EF=,AE=GD=1,则可得BE=2GE=3,最后在Rt△AEB中,利用勾股定理可算出AB的长.
43.64°
解:∵直线AB与的相切于点,
∴∠ACO=90°,
又∵∠ACD=32°,
∴∠OCD=∠ACO-∠ACD=58°,
∵OC=OD,
∴∠OCD=∠ODC=58°,
∴∠COD=180°-∠OCD-∠ODC=64°.
故答案为:64°.
由圆的切线垂直于经过切点的半径可得∠ACO=90°,然后根据角的构成可算出∠OCD=∠ACO-∠ACD=58°,由等边对等角得∠OCD=∠ODC=58°,最后根据三角形的内角和定理可算出∠COD的度数.
44.9
解:由题意得,
去分母得1+x=2x-8,
移项、合并同类项,得x=9,
经检验,x=9是原分式方程的根.
故答案为:9.
由分式的值为2可列出关于字母x的分式方程,方程两边同时乘以x-4约去分母将分式方程转化为整式方程,解整式方程求出x的值,再检验即可得出答案.
45.
解:由题意可得: 随机从中摸一个球,恰好摸到黑球的概率是.
故答案为:.
根据概率公式,用袋中黑色小球的个数比上袋中小球的总个数即可得出随机从中摸一个球,恰好摸到黑球的概率.
46.
a2-9=(a+3)(a-3)。
故答案为:(a+3)(a-3)。
由平方差公式:a2-b2=(a+b)(a-b)可得。
47.
解:a2﹣3a=a(a﹣3).故答案为:a(a﹣3).
根据提取公因式法进行因式分解即可。
48.
解:列表如下:
1 2 3
1 — 3 4
2 3 — 5
3 4 5 —
由上表可知,共有6种等可能得结果,其中偶数有2种,
数字之和是偶数的概率是,
故答案为:.
本题考查列表法求概率.先列表求出从中随机抽取2张,数字之和的全部结果数,再数出偶数结果数,再利用简单概率公式进行计算可求出概率.
49.1
解:,
去分母得,,
移项、合并同类项得,
解得.
检验:把代入,
是原分式方程的解.
故答案为:.
本题考查分式方程的解法.先去分母化成一元一次方程,移项、合并同类项得,再将x的系数化为1可求出x的值,再进行检验可求出方程的解.
50.
解:,
故答案为:.
利用提公因式法因式分解即可.
同课章节目录
