专项4 解答题1 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项4 解答题1 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 837.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 00:00:00 | ||
图片预览




文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项4 应用题1 (浙江中考真题+中考模拟)
一、解答题
1.(2024·浙江)如图1,反比例函数的图象经过点,射线与反比例函数的图象交于另一点,射线与y轴交于点C,,轴于点D.
(1)填空:
①k的值为__________.
②_________;直线的函数解析式为__________.
(2)如图2,M是线段上方反比例函数图象上一动点,过点M作直线轴,与交于点N,连接.求面积的最大值.
2.(2024·浙江)图1是一把可折叠的哑铃椅,其侧面可抽象成图2,为支撑杆,M为靠背的中点,点N可在斜支柱上滑动,通过调节螺母可将点N固定在斜支柱上的六个孔位处,靠背随之绕点C转动,当点N位于第一个孔位处时,;当点N位于最后一个孔位处时,.已知,,,坐凳与水平地面l平行.
(1)在点N从第一个孔位滑动到最后一个孔位的过程中,求点M所运动的路径长(结果保留π)
(2)在转动的过程中,求点H到水平地面l的最大距离.
(结果精确到.参考数据:.)
3.(2024·浙江)已知关于x的方程有两个正整数根(m是整数).的三边a,b,c满足:.
(1)求m的值.
(2)求的面积(结果允许保留双重根号),
4.(2025九下·钱塘模拟)已知二次函数(t为常数)的图象经过的图象顶点.
(1)求的值.
(2)若二次函数的图象经过点,求的最小值.
(3)若二次函数在时,,求的取值范围.
5.(2025九下·钱塘模拟)已知线段满足,且.
(1)求线段的长.
(2)若线段是线段的比例中项,求线段的长.
6.(2025九下·浙江模拟)设二次函数(是常数),已知函数值和自变量的部分对应取值如表所示.
... 0 1 2 ...
... 1 1 ...
(1)若,求二次函数的表达式.
(2)若当时,有最小值,求的值.
(3)求证:.
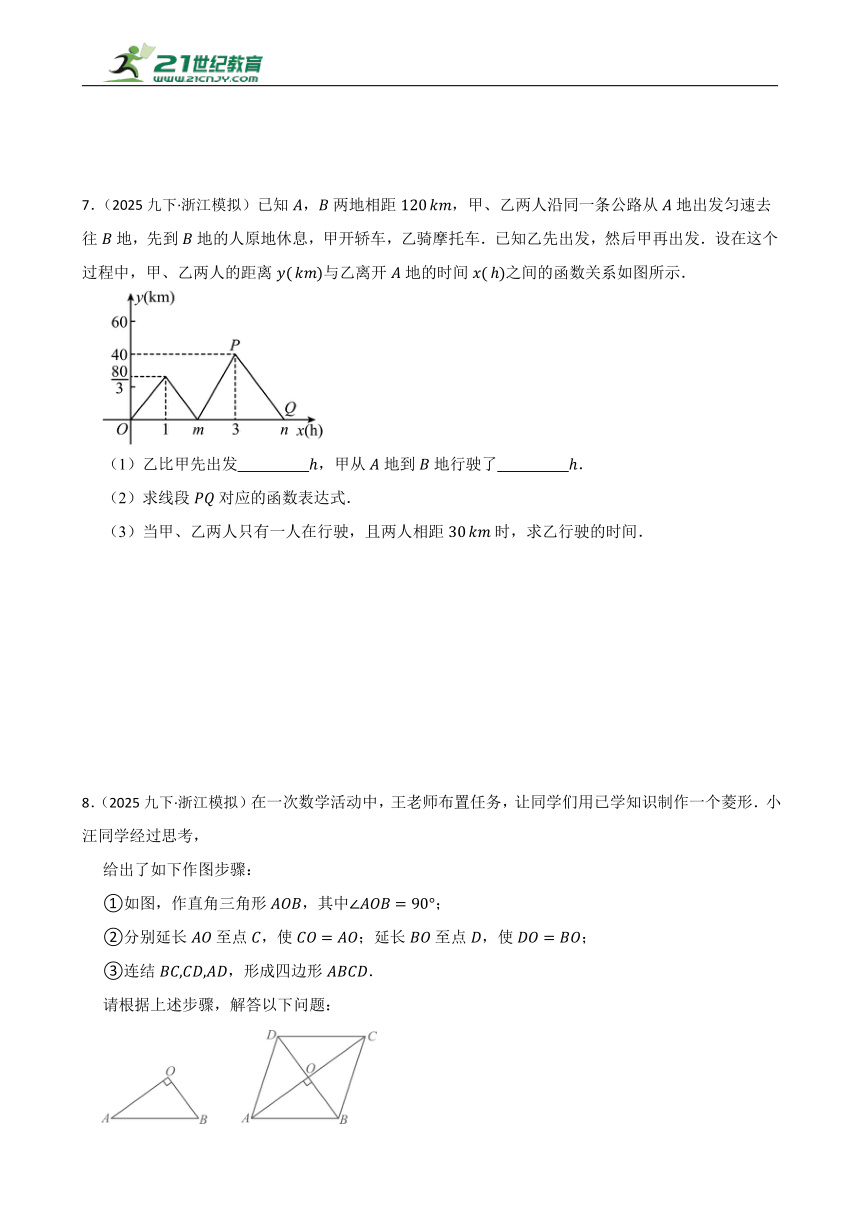
7.(2025九下·浙江模拟)已知,两地相距,甲、乙两人沿同一条公路从地出发匀速去往地,先到地的人原地休息,甲开轿车,乙骑摩托车.已知乙先出发,然后甲再出发.设在这个过程中,甲、乙两人的距离与乙离开地的时间之间的函数关系如图所示.
(1)乙比甲先出发 ,甲从地到地行驶了 .
(2)求线段对应的函数表达式.
(3)当甲、乙两人只有一人在行驶,且两人相距时,求乙行驶的时间.
8.(2025九下·浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,
给出了如下作图步骤:
①如图,作直角三角形,其中;
②分别延长至点,使;延长至点,使;
③连结,形成四边形.
请根据上述步骤,解答以下问题:
(1)判断四边形是否为菱形,并说明理由.
(2)若,求点到的距离.
9.(2025·鹿城模拟)已知二次函数的图象经过点.
(1)求二次函数解析式及其对称轴;
(2)将函数图象向上平移个单位长度,图象与轴相交于点(在原点左侧),当时,求的值;
(3)当时,二次函数的最小值为,求的值.
10.(2025九下·宁波模拟)“超速已成为马路主要安全隐患之一”.如图,一条公路建成通车,在某笔直路段MN限速100千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点,从观测点测得一小车从点行驶到点用了5秒钟,已知米,则此车超速了吗 请说明理由.(参考数据:)
11.(2025·衢江模拟)已知二次函数,
(1)若抛物线的对称轴为直线,
①当函数图象过点时,求该二次函数的关系式;
②当时,函数的最小值为,求的最大值.
(2)若当时,取值范围是,且该二次函数图象经过,两点,,求的取值的范围.
12.(2025九下·浙江模拟)在2024年巴黎奥运会上,我国体育健儿顽强拼搏、奋勇争先、不负使命,勇夺40枚金牌.为了致敬奥运健儿,弘扬体育精神,某校举办了一分钟跳绳比赛.学校随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了统计表和统计图(如图).
一分钟跳绳次数的频数表
等级 次数 频数
不合格 4
合格 10
良好
优秀 12
一分钟跳绳次数的频数直方图
请根据上述信息,解答下列问题:
(1)求的值,并把一分钟跳绳次数的频数直方图补充完整.
(2)若该校有800名学生,估计该校学生一分钟跳绳次数达到合格及以上的人数为 .
(3)在本次比赛结果为“优秀”等级的学生中,有4位同学一分钟跳绳的次数达190次以上,其中男生和女生各占一半,现准备从这四位同学中选2位参加比赛.请用列表或画树状图的方法,求选出的2位同学恰好性别不同的概率.
13.(2025·衢州模拟)如图,在中,是内一点,连结CD,将线段CD绕点逆时针旋转到CE,使,连结.
(1)求证:.
(2)当时,求与的度数和.
14.(2025·鹿城模拟)某校为了解学生的劳动教育情况,对九年级学生寒假期间“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(:;:;:;:,单位:分钟)进行统计,绘制了如下不完整的统计图.
(1)求出本次抽样的学生人数并补全条形统计图;
(2)已知该校九年级有名学生,请估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生有多少人?
(3)若组中有名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.
15.(2025九下·浙江模拟)如图,一次函数的图象与反比例函数的图象相交于点,
(1)求和的值.
(2)横坐标为的点是反比例函数图象上的一点.现将点向下平移.当点落在一次函数图象上时,求向下平移的距离.
16.(2025九下·宁波模拟)冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜,深受市民喜爱。上市时,王经理按市场价格6元/千克收购了2000千克苹果放入冷库中。据预测,苹果的市场价格每天每千克将上涨0.2元,但冷库存放这批苹果每天需要支出各种费用160元,而且苹果在冷库中最多可以保存50天,同时,每天有10千克的苹果损坏不能出售。
(1)若存放天后,将这批苹果一次性出售,设这批苹果的销售总金额为元,试写出与之间的函数解析式;
(2)王经理想获得3850元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
17.(2025九下·宁波模拟)如果二次函数的图像经过点(-1,0),那么称此二次函数为“定点抛物线”.
(1)试判断二次函数的图像是否为“定点抛物线”.
(2)若定点抛物线与轴只有一个公共点,求的值.
18.(2025·衢州模拟)对于二次函数.
(1)若二次函数的图象经过了三点中的某一个点.
①判定该二次函数的图象应经过上述三点中的哪一个点,并说明理由.
②当时,该函数的最小值是-3,求的值.
(2)若二次函数的图象经过点,求当时,的取值范围.
19.(2025·衢州模拟)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
20.(2025·衢州模拟)某校在新学期之初举办了一场以“环保”为主题的综合实践知识竞赛,并把随机抽取的若干八年级学生的竞赛成绩进行整理,绘制成如下不完整的统计表和统计图.
组别 成绩(分) 频数
2
14
10
(1)写出a,b的值,并补全频数直方图.
(2)求扇形统计图中,组所对应的圆心角度数.
(3)该校八年级共有480人,根据统计信息,估计该校八年级学生的竞赛成绩在组的人数.
21.(2025·鹿城模拟)解方程组.
22.(2025·衢江模拟)某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A篮球,B足球,C排球,D羽毛球,E乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
(1)本次随机抽取多少名学生进行调查?并补全条形统计图;
(2)求扇形统计图中C对应圆心角的度数;
(3)若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
23.(2025·镇海区模拟)杭州纸伞馆有制作精美的纸伞,如图,四条长度相等的伞骨围成菱形,伞骨连结点固定在伞柄顶端,伞圈能沿着伞柄滑动.小聪通过测量发现:当伞完全张开时,伞柄的中点到伞骨连结点的距离都等于的一半,若夹角,求的度数.
答案解析部分
1.(1)①;②;
(2)
2.(1)
(2)
3.(1)
(2)或
4.(1)
(2)的最小值为
(3)的取值范围是
5.(1)线段的长为12,线段的长为3
(2)线段的长为6
6.(1)解:由条件可知抛物线的对称轴直线为
即
若 即 时,
解得,
∴二次函数的表达式
(2)解:根据题意,
当 时,二次函数图象开口象限,对称轴直线 1处取得最小值
解得,
当 时,二次函数图象开口向下,对称轴直线为 ,离对称轴直线越远,函数值越小,
∴当 4时,取得最小值
解得,
综上所述:或;
(3)证明:由条件可知
,
∴关于a的二次函数图象开口向下,函数的最大值为
(1)根据表格信息得到对称轴直线为 , 即 时, 运用待定系数法即可求解;
(2)根据题意得到 分类讨论:当 时,二次函数图象开口象限,对称轴直线 =1处取得最小值 当a<0时,二次函数图象 开口向下,对称轴直线为 离对称轴直线越远, 函数值越小, 当 4时,取得最小值 代入求值即可;
(3)根据题意当 时, m, 当 时, 得,根据二次函数图象的性质即可求解.
7.(1)1;2
(2)解:根据题意,
∴Q(4.5,0),
设线段PQ对应的函数表达式为 将P,Q的坐标分别代入得:
解得
∴线段PQ对应的函数表达式为
(3)解:①甲没有出发时,得:
解得
不合题意;
②甲到达B地时,得: 解得
综上所述,当甲、乙两人只有一人在行驶,且两人相距30km时,乙行驶的时间为 小时.
(1)由图象可知,乙比甲先出发1小时;甲到达B地用了: (小时),
故答案为: 1; 2;
(1)根据题意列式计算即可求解;
(2)利用待定系数法求函数解析式即可;
(3)根据题意,当甲、乙两人只有一人在行驶时,实际上就是乙一个人在行驶,故分甲没有出发时和甲到达B地时两种情况,列方程求出x的值.
8.(1)解:四边形是菱形,理由为:
∵AO=CO,BO=OD,
∴ABCD是平行四边形,
又∵∠AOB=90°,
∴ABCD是菱形;
(2)解:∵AO=OC=,
∴,
∴BD=6,
设点C到AB的距离为h,
∴,即,
即.
(1)根据对角线互相垂直平分的四边形是菱形解答即可;
(2)先根据勾股定理求出OB长,然后求出BD长,再根据菱形的面积计算距离即可.
9.(1)解:将代入函数表达式得:,
解得,,
即抛物线的表达式为:,
则抛物线的对称轴为直线;
(2)解:当时,
设点、,
则平移后抛物线的对称轴仍然为直线,则,
则点、的坐标分别为:、,
则新抛物线的表达式为:,
即;
(3)解:由(1)知,抛物线的顶点为,
当,即时,
抛物线在顶点处取得最小值,即,则;
当时,即时,
则抛物线在时取得最小值,即,
解得:(舍去)或6(舍去),
综上,.
(1)由题意,将点(1,-4)代入二次函数的解析式可得关于b的方程,解方程求出b的值,再根据抛物线的对称轴为直线计算即可求解;
(2)根据AO:BO=1:4可设点、,则平移后抛物线的对称轴仍然为直线,通过对称轴不变求出t的值,再根据A、B两点的坐标结合二次函数的交点式可求解;
(3)由(1)的结论可先求出抛物线的顶点为,再分和两种情况来讨论函数的最小值即可求解.
(1)解:将代入函数表达式得:,则,
即抛物线的表达式为:,
则抛物线的对称轴为直线;
(2)解:当时,
设点、,
则平移后抛物线的对称轴仍然为直线,则,
则点、的坐标分别为:、,
则新抛物线的表达式为:,
即;
(3)解:由(1)知,抛物线的顶点为,
当,即时,
抛物线在顶点处取得最小值,即,则;
当时,即时,
则抛物线在时取得最小值,即,
解得:(舍去)或6(舍去),
综上,.
10.解:此车超速.
理由如下:过C作CH⊥MN,
∵∠CBN=60°,BC=400米,
∴CH=BC sin60°=400×=200(米),
BH=BC cos60°=200(米),
∵∠CAN=45°,
∴AH=CH=200米,
∴AB=200﹣200≈146.4(m),
∵100千米/小时=m/s,
∴(m)<146.4(m),
∴此车超速.
过C作 通过解直角三角形先分别计算出CH和BH,再根据速度等于路程除以时间即可求出小车的速速,最后比较即可得出答案,但需要注意单位的换算.
11.(1)解:①由题意,得:,
解得:,
∴;
②∵,
∴当时,有最小值为:;
∵时,函数的最小值为,
∴,
解得:,
∴的最大值为;
(2)解:∵当时,取值范围是,
∴当时,,
∴抛物线的对称轴为直线,
∵,
∴抛物线的开口向上,抛物线上的点离对称越远,函数值越大,
∵二次函数图象经过,两点,且,
∴,
解得:或;
故或.
(1)①由题意,用待定系数法即可求解;
②根据①中求得的解析式得:当时,有最小值为,根据当时,函数的最小值为,得到,解之即可求解;
(2)根据时,取值范围是,求出抛物线的对称轴,根据二次函数的增减性,求出的取值的范围即可.
(1)解:①由题意,得:,
解得:,
∴;
②∵,
∴当时,有最小值为:;
∵时,函数的最小值为,
∴,
解得:,
∴的最大值为;
(2)解:∵当时,取值范围是,
∴当时,,
∴抛物线的对称轴为直线,
∵,
∴抛物线的开口向上,抛物线上的点离对称越远,函数值越大,
∵二次函数图象经过,两点,且,
∴,
解得:或;
故或.
12.(1)解: 由题意得,
补充图如下:
一分钟跳绳次数的频数直方图
(2)720人
(3)解:列表如下:
男1 男2 女1 女2
男1 (男1, 男2) (男1, 女1) (男1, 女2)
男2 (男2, 男1) (男2, 女1) (男2, 女2
女1 (女1, 男1) (女1, 男2) (女1, 女2)
女2 (女2, 男1) (女2, 男2) (女2, 女1)
共有12种等可能的结果,其中选出的2位同学恰好性别不同的结果有84种,
∴选出的2位同学恰好性别相同的概率为
(2)∵40名学生中有4人不合格,∴估计该校学生一分钟跳绳次数达到合格的人数约 (人) ,
故答案为: 720;
(1)用总人数减去其他等级人数即可求解a值,然后补充统计图即可;
(2)用全校总人数乘以样本中一分钟跳绳次数达到合格所占的比例求解即可;
(3)列表求得所有等可能的结果,找出满足条件的可能结果数,然后利用概率公式求解即可
13.(1)解:∵∠DCE=∠ACB,
∴∠DCE-∠DCB=∠ACB-∠DCB,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵∠CBA=60°,CA=CB,
∴△CAB是等边三角形,
∴∠CAB=60°,
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
(1)先利用等式性质证得∠ACD=∠BCE,再利用SAS证明;
(2)先证明△CAB是等边三角形,求得∠CAB=60°,再根据全等三角形的性质证得∠CAD=∠CBE,然后利用两角之和求得∠CBE+∠BAD.
14.(1)解:本次抽样的学生人数为(人),
组的人数为(人),
补全条形统计图如下图所示;
(2)解:(人),
估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生约人;
(3)解:由题意得,有名女生,名男生,
列表如下:
男 男 女 女 女
男 (男,男) (男,女) (男,女) (男,女)
男 (男,男) (男,女) (男,女) (男,女)
女 (女,男) (女,男) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女)
共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,
抽取的两名同学中恰好是一名女生和一名男生的概率为.
由条形统计图可知组有人,由扇形统计图可知组人数占总人数的,然后根据样本容量=频数÷百分数可计算出抽查的学生的总人数;再根据样本容量等于各小组频数之和可求得组的人数,根据组的人数,于是可将条形统计图补充完整;
根据条形统计图可知被抽查到的学生中参加家务劳动的时间在到分钟的人数共有人,占被抽查的总人数的,然后用样本估计总体可求解;
由题意,用列表法把所有可能出现的情况表示出来,共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,然后用概率公式计算即可求解.
(1)解:本次抽样的学生人数为(人),
组的人数为(人),
补全条形统计图如下图所示;
(2)解:(人),
估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生约人;
(3)解:由题意得,有名女生,名男生,
列表如下:
男 男 女 女 女
男
(男,男) (男,女) (男,女) (男,女)
男 (男,男)
(男,女) (男,女) (男,女)
女 (女,男) (女,男)
(女,女) (女,女)
女 (女,男) (女,男) (女,女)
(女,女)
女 (女,男) (女,男) (女,女) (女,女)
共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,
抽取的两名同学中恰好是一名女生和一名男生的概率为.
15.(1)解:∵一次函数 的图象过点.
解得
∴一次函数解析式为
∵与反比例函数 的图象过点.
解得
(2)解:由 (1) 知,
∴反比例函数解析式为
∵点B的横坐标为3,且点B在反比例函数图象上,
即
设点B向下平移了m个单位,
解得
∴向下平移的距离为
(1)把. )代入一次函数,反比例函数解析式即可求解;
(2)根据题意得到 根据点的平移得到平移后 代入一次函数解析式即可求解
16.(1)
(2)解:
(不合题意,舍去)
答:需将这批苹果存放35天后出售。
(3)
$
所以当时,最大,即存放45天后出售可获得最大利润,最大利润为4050元。
(1)根据苹果的单价乘以苹果的数量,可得函数关系式;
(2)根据利润等于销售总金额减去收购成本、减去每天的费用,可得方程,根据解方程,可得答案;
(3)根据利润等于销售总金额减去收购成本、减去每天的费用,可得二次函数,根据二次函数的性质,可得答案.
17.(1)∵当x=-1时,y=2+5-7=0,
∴二次函数图象经过点(-1,0),
∴二次函数y=2x2-5x-7是定点抛物线.
(2)由题意得,
∴
∴
(1) 把 1代入抛物线解析式,判断y的值是否为0,即可解决问题.
(2) 因为 与x轴只有一个公共点,所以 是抛物线顶点,所以抛物线解析式为 由此即可解决问题.
18.(1)解:①当时,,不合题意,舍去;
当时,,所以,符合合题意,
这时二次函数的表达式是;
当时,,所以,不合题意,舍去;
②因为二次函数的图象开口向上,对称轴是直线,
与y轴交于点(0,-3),
所以当x>1时,y随x的增大而增大,点(0,-3)关于直线x=1的对称点为(2,-3),
又当x≥m时,该函数的最小值是-3,
所以m=2.
(2)解:当x=n时,p=an2-2an-3;
当x=n+3时,q=a(n+3)2-2a(n+3)-3;
∴q=an2+4an+3a-3,
∴p-q=-6an-3a=-3a(2n+1)<0
∵a>0,
∴2n+1>0,解得:n>-0.5.
(1)①分别用x=2、x=1、x=-1代入函数解析式中,求出函数值,与相应的纵坐标比较后得出结论;
② 先根据二次函数解析式,求出对称轴,与y轴的交点,再结合增减性求得m的值;
(2)分别求出当x=n与x=n+3时的函数值,再根据列出关于n的不等式求解.
19.(1)解:甲机器人速度:30÷6=5(米/秒),
乙机器人速度:(70-7)÷18=3.5(米/秒),
甲机器人表演的时长为18-70÷5=18-14=4秒.
(2)解:当甲,乙机器人同时到达终点时,相遇点距离展展台终点的终点的距离为0;
当甲,乙机器人相遇在甲表演点时,70-30=40;
当甲,乙机器人相遇在甲表演点之前时,
乙机器人的函数表达式:y=+7,
甲机器人的函数表达式:y=5x(0≤x≤6);
当时,得,当,,
∴,
答:当甲、乙机器人相遇时,距离终点,40米或0米.
(1)先根据图象得出甲、乙机器人的路程和时间,再计算速度,然后计算出甲机器人表演的时长;
(2)结合图象分为“甲机器人表演前”、“表演时”、“到达终点时”三种情况,分别计算.
20.(1)a=4,b=20.
补全条形统计图如下:
(2)解:.
∴组所对应的圆心角度数为14.4°.
(3)解:0.4×480=192(人),
∴ 估计该校八年级学生的竞赛成绩在组的人数为192人.
解:(1)班级总人数为10÷20%=30,
∴b=50×40%=20,
∴a=50-2-14-20-10=4.
补全条形统计图如下:
(1)根据这一组的人数与所占百分比,可求得班级总人数,再根据这一组所占的百分比求得这一组的人数,然后利用求得班级总人数减去其他各组人数求得这一组人数,再补全条形统计图;
(2)根据A组的频数除以总数乘360度即可;
(3)根据D组所占百分比乘以八年级总人数即可.
21.解:,
将②代入①中得
.
解得.
将代入②,
得,.
∴原方程组的解为:.
观察原方程组可知,方程②中的x用含y的代数式表示出来,于是可将方程②代入方程①可得关于y的一元一次方程,解这个方程求出y的值,把y的值代入方程②求出x的值,再写出结论即可.
22.(1)解:本次调查的样本容量为:;
最喜欢“B足球”的学生人数为:人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为:
;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
(1)根据样本容量=频数÷百分数可得,样本容量=用最喜欢“D羽毛球”的学生人数除以其所占的百分比;根据各小组的频数之和等于样本容量可求出最喜欢“B足球”的学生人数,然后可将条形图补充完整;
(2)根据圆心角=360°×最喜欢“C排球”的学生人数所占的百分比计算即可求解;
(3)用样本估计总体即可求解.
(1)解:本次调查的样本容量是;
最喜欢“B足球”的学生人数为人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
23.的度数为
专项4 应用题1 (浙江中考真题+中考模拟)
一、解答题
1.(2024·浙江)如图1,反比例函数的图象经过点,射线与反比例函数的图象交于另一点,射线与y轴交于点C,,轴于点D.
(1)填空:
①k的值为__________.
②_________;直线的函数解析式为__________.
(2)如图2,M是线段上方反比例函数图象上一动点,过点M作直线轴,与交于点N,连接.求面积的最大值.
2.(2024·浙江)图1是一把可折叠的哑铃椅,其侧面可抽象成图2,为支撑杆,M为靠背的中点,点N可在斜支柱上滑动,通过调节螺母可将点N固定在斜支柱上的六个孔位处,靠背随之绕点C转动,当点N位于第一个孔位处时,;当点N位于最后一个孔位处时,.已知,,,坐凳与水平地面l平行.
(1)在点N从第一个孔位滑动到最后一个孔位的过程中,求点M所运动的路径长(结果保留π)
(2)在转动的过程中,求点H到水平地面l的最大距离.
(结果精确到.参考数据:.)
3.(2024·浙江)已知关于x的方程有两个正整数根(m是整数).的三边a,b,c满足:.
(1)求m的值.
(2)求的面积(结果允许保留双重根号),
4.(2025九下·钱塘模拟)已知二次函数(t为常数)的图象经过的图象顶点.
(1)求的值.
(2)若二次函数的图象经过点,求的最小值.
(3)若二次函数在时,,求的取值范围.
5.(2025九下·钱塘模拟)已知线段满足,且.
(1)求线段的长.
(2)若线段是线段的比例中项,求线段的长.
6.(2025九下·浙江模拟)设二次函数(是常数),已知函数值和自变量的部分对应取值如表所示.
... 0 1 2 ...
... 1 1 ...
(1)若,求二次函数的表达式.
(2)若当时,有最小值,求的值.
(3)求证:.
7.(2025九下·浙江模拟)已知,两地相距,甲、乙两人沿同一条公路从地出发匀速去往地,先到地的人原地休息,甲开轿车,乙骑摩托车.已知乙先出发,然后甲再出发.设在这个过程中,甲、乙两人的距离与乙离开地的时间之间的函数关系如图所示.
(1)乙比甲先出发 ,甲从地到地行驶了 .
(2)求线段对应的函数表达式.
(3)当甲、乙两人只有一人在行驶,且两人相距时,求乙行驶的时间.
8.(2025九下·浙江模拟)在一次数学活动中,王老师布置任务,让同学们用已学知识制作一个菱形.小汪同学经过思考,
给出了如下作图步骤:
①如图,作直角三角形,其中;
②分别延长至点,使;延长至点,使;
③连结,形成四边形.
请根据上述步骤,解答以下问题:
(1)判断四边形是否为菱形,并说明理由.
(2)若,求点到的距离.
9.(2025·鹿城模拟)已知二次函数的图象经过点.
(1)求二次函数解析式及其对称轴;
(2)将函数图象向上平移个单位长度,图象与轴相交于点(在原点左侧),当时,求的值;
(3)当时,二次函数的最小值为,求的值.
10.(2025九下·宁波模拟)“超速已成为马路主要安全隐患之一”.如图,一条公路建成通车,在某笔直路段MN限速100千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点,从观测点测得一小车从点行驶到点用了5秒钟,已知米,则此车超速了吗 请说明理由.(参考数据:)
11.(2025·衢江模拟)已知二次函数,
(1)若抛物线的对称轴为直线,
①当函数图象过点时,求该二次函数的关系式;
②当时,函数的最小值为,求的最大值.
(2)若当时,取值范围是,且该二次函数图象经过,两点,,求的取值的范围.
12.(2025九下·浙江模拟)在2024年巴黎奥运会上,我国体育健儿顽强拼搏、奋勇争先、不负使命,勇夺40枚金牌.为了致敬奥运健儿,弘扬体育精神,某校举办了一分钟跳绳比赛.学校随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了统计表和统计图(如图).
一分钟跳绳次数的频数表
等级 次数 频数
不合格 4
合格 10
良好
优秀 12
一分钟跳绳次数的频数直方图
请根据上述信息,解答下列问题:
(1)求的值,并把一分钟跳绳次数的频数直方图补充完整.
(2)若该校有800名学生,估计该校学生一分钟跳绳次数达到合格及以上的人数为 .
(3)在本次比赛结果为“优秀”等级的学生中,有4位同学一分钟跳绳的次数达190次以上,其中男生和女生各占一半,现准备从这四位同学中选2位参加比赛.请用列表或画树状图的方法,求选出的2位同学恰好性别不同的概率.
13.(2025·衢州模拟)如图,在中,是内一点,连结CD,将线段CD绕点逆时针旋转到CE,使,连结.
(1)求证:.
(2)当时,求与的度数和.
14.(2025·鹿城模拟)某校为了解学生的劳动教育情况,对九年级学生寒假期间“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(:;:;:;:,单位:分钟)进行统计,绘制了如下不完整的统计图.
(1)求出本次抽样的学生人数并补全条形统计图;
(2)已知该校九年级有名学生,请估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生有多少人?
(3)若组中有名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.
15.(2025九下·浙江模拟)如图,一次函数的图象与反比例函数的图象相交于点,
(1)求和的值.
(2)横坐标为的点是反比例函数图象上的一点.现将点向下平移.当点落在一次函数图象上时,求向下平移的距离.
16.(2025九下·宁波模拟)冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜,深受市民喜爱。上市时,王经理按市场价格6元/千克收购了2000千克苹果放入冷库中。据预测,苹果的市场价格每天每千克将上涨0.2元,但冷库存放这批苹果每天需要支出各种费用160元,而且苹果在冷库中最多可以保存50天,同时,每天有10千克的苹果损坏不能出售。
(1)若存放天后,将这批苹果一次性出售,设这批苹果的销售总金额为元,试写出与之间的函数解析式;
(2)王经理想获得3850元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
17.(2025九下·宁波模拟)如果二次函数的图像经过点(-1,0),那么称此二次函数为“定点抛物线”.
(1)试判断二次函数的图像是否为“定点抛物线”.
(2)若定点抛物线与轴只有一个公共点,求的值.
18.(2025·衢州模拟)对于二次函数.
(1)若二次函数的图象经过了三点中的某一个点.
①判定该二次函数的图象应经过上述三点中的哪一个点,并说明理由.
②当时,该函数的最小值是-3,求的值.
(2)若二次函数的图象经过点,求当时,的取值范围.
19.(2025·衢州模拟)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
20.(2025·衢州模拟)某校在新学期之初举办了一场以“环保”为主题的综合实践知识竞赛,并把随机抽取的若干八年级学生的竞赛成绩进行整理,绘制成如下不完整的统计表和统计图.
组别 成绩(分) 频数
2
14
10
(1)写出a,b的值,并补全频数直方图.
(2)求扇形统计图中,组所对应的圆心角度数.
(3)该校八年级共有480人,根据统计信息,估计该校八年级学生的竞赛成绩在组的人数.
21.(2025·鹿城模拟)解方程组.
22.(2025·衢江模拟)某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A篮球,B足球,C排球,D羽毛球,E乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
(1)本次随机抽取多少名学生进行调查?并补全条形统计图;
(2)求扇形统计图中C对应圆心角的度数;
(3)若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
23.(2025·镇海区模拟)杭州纸伞馆有制作精美的纸伞,如图,四条长度相等的伞骨围成菱形,伞骨连结点固定在伞柄顶端,伞圈能沿着伞柄滑动.小聪通过测量发现:当伞完全张开时,伞柄的中点到伞骨连结点的距离都等于的一半,若夹角,求的度数.
答案解析部分
1.(1)①;②;
(2)
2.(1)
(2)
3.(1)
(2)或
4.(1)
(2)的最小值为
(3)的取值范围是
5.(1)线段的长为12,线段的长为3
(2)线段的长为6
6.(1)解:由条件可知抛物线的对称轴直线为
即
若 即 时,
解得,
∴二次函数的表达式
(2)解:根据题意,
当 时,二次函数图象开口象限,对称轴直线 1处取得最小值
解得,
当 时,二次函数图象开口向下,对称轴直线为 ,离对称轴直线越远,函数值越小,
∴当 4时,取得最小值
解得,
综上所述:或;
(3)证明:由条件可知
,
∴关于a的二次函数图象开口向下,函数的最大值为
(1)根据表格信息得到对称轴直线为 , 即 时, 运用待定系数法即可求解;
(2)根据题意得到 分类讨论:当 时,二次函数图象开口象限,对称轴直线 =1处取得最小值 当a<0时,二次函数图象 开口向下,对称轴直线为 离对称轴直线越远, 函数值越小, 当 4时,取得最小值 代入求值即可;
(3)根据题意当 时, m, 当 时, 得,根据二次函数图象的性质即可求解.
7.(1)1;2
(2)解:根据题意,
∴Q(4.5,0),
设线段PQ对应的函数表达式为 将P,Q的坐标分别代入得:
解得
∴线段PQ对应的函数表达式为
(3)解:①甲没有出发时,得:
解得
不合题意;
②甲到达B地时,得: 解得
综上所述,当甲、乙两人只有一人在行驶,且两人相距30km时,乙行驶的时间为 小时.
(1)由图象可知,乙比甲先出发1小时;甲到达B地用了: (小时),
故答案为: 1; 2;
(1)根据题意列式计算即可求解;
(2)利用待定系数法求函数解析式即可;
(3)根据题意,当甲、乙两人只有一人在行驶时,实际上就是乙一个人在行驶,故分甲没有出发时和甲到达B地时两种情况,列方程求出x的值.
8.(1)解:四边形是菱形,理由为:
∵AO=CO,BO=OD,
∴ABCD是平行四边形,
又∵∠AOB=90°,
∴ABCD是菱形;
(2)解:∵AO=OC=,
∴,
∴BD=6,
设点C到AB的距离为h,
∴,即,
即.
(1)根据对角线互相垂直平分的四边形是菱形解答即可;
(2)先根据勾股定理求出OB长,然后求出BD长,再根据菱形的面积计算距离即可.
9.(1)解:将代入函数表达式得:,
解得,,
即抛物线的表达式为:,
则抛物线的对称轴为直线;
(2)解:当时,
设点、,
则平移后抛物线的对称轴仍然为直线,则,
则点、的坐标分别为:、,
则新抛物线的表达式为:,
即;
(3)解:由(1)知,抛物线的顶点为,
当,即时,
抛物线在顶点处取得最小值,即,则;
当时,即时,
则抛物线在时取得最小值,即,
解得:(舍去)或6(舍去),
综上,.
(1)由题意,将点(1,-4)代入二次函数的解析式可得关于b的方程,解方程求出b的值,再根据抛物线的对称轴为直线计算即可求解;
(2)根据AO:BO=1:4可设点、,则平移后抛物线的对称轴仍然为直线,通过对称轴不变求出t的值,再根据A、B两点的坐标结合二次函数的交点式可求解;
(3)由(1)的结论可先求出抛物线的顶点为,再分和两种情况来讨论函数的最小值即可求解.
(1)解:将代入函数表达式得:,则,
即抛物线的表达式为:,
则抛物线的对称轴为直线;
(2)解:当时,
设点、,
则平移后抛物线的对称轴仍然为直线,则,
则点、的坐标分别为:、,
则新抛物线的表达式为:,
即;
(3)解:由(1)知,抛物线的顶点为,
当,即时,
抛物线在顶点处取得最小值,即,则;
当时,即时,
则抛物线在时取得最小值,即,
解得:(舍去)或6(舍去),
综上,.
10.解:此车超速.
理由如下:过C作CH⊥MN,
∵∠CBN=60°,BC=400米,
∴CH=BC sin60°=400×=200(米),
BH=BC cos60°=200(米),
∵∠CAN=45°,
∴AH=CH=200米,
∴AB=200﹣200≈146.4(m),
∵100千米/小时=m/s,
∴(m)<146.4(m),
∴此车超速.
过C作 通过解直角三角形先分别计算出CH和BH,再根据速度等于路程除以时间即可求出小车的速速,最后比较即可得出答案,但需要注意单位的换算.
11.(1)解:①由题意,得:,
解得:,
∴;
②∵,
∴当时,有最小值为:;
∵时,函数的最小值为,
∴,
解得:,
∴的最大值为;
(2)解:∵当时,取值范围是,
∴当时,,
∴抛物线的对称轴为直线,
∵,
∴抛物线的开口向上,抛物线上的点离对称越远,函数值越大,
∵二次函数图象经过,两点,且,
∴,
解得:或;
故或.
(1)①由题意,用待定系数法即可求解;
②根据①中求得的解析式得:当时,有最小值为,根据当时,函数的最小值为,得到,解之即可求解;
(2)根据时,取值范围是,求出抛物线的对称轴,根据二次函数的增减性,求出的取值的范围即可.
(1)解:①由题意,得:,
解得:,
∴;
②∵,
∴当时,有最小值为:;
∵时,函数的最小值为,
∴,
解得:,
∴的最大值为;
(2)解:∵当时,取值范围是,
∴当时,,
∴抛物线的对称轴为直线,
∵,
∴抛物线的开口向上,抛物线上的点离对称越远,函数值越大,
∵二次函数图象经过,两点,且,
∴,
解得:或;
故或.
12.(1)解: 由题意得,
补充图如下:
一分钟跳绳次数的频数直方图
(2)720人
(3)解:列表如下:
男1 男2 女1 女2
男1 (男1, 男2) (男1, 女1) (男1, 女2)
男2 (男2, 男1) (男2, 女1) (男2, 女2
女1 (女1, 男1) (女1, 男2) (女1, 女2)
女2 (女2, 男1) (女2, 男2) (女2, 女1)
共有12种等可能的结果,其中选出的2位同学恰好性别不同的结果有84种,
∴选出的2位同学恰好性别相同的概率为
(2)∵40名学生中有4人不合格,∴估计该校学生一分钟跳绳次数达到合格的人数约 (人) ,
故答案为: 720;
(1)用总人数减去其他等级人数即可求解a值,然后补充统计图即可;
(2)用全校总人数乘以样本中一分钟跳绳次数达到合格所占的比例求解即可;
(3)列表求得所有等可能的结果,找出满足条件的可能结果数,然后利用概率公式求解即可
13.(1)解:∵∠DCE=∠ACB,
∴∠DCE-∠DCB=∠ACB-∠DCB,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵∠CBA=60°,CA=CB,
∴△CAB是等边三角形,
∴∠CAB=60°,
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
(1)先利用等式性质证得∠ACD=∠BCE,再利用SAS证明;
(2)先证明△CAB是等边三角形,求得∠CAB=60°,再根据全等三角形的性质证得∠CAD=∠CBE,然后利用两角之和求得∠CBE+∠BAD.
14.(1)解:本次抽样的学生人数为(人),
组的人数为(人),
补全条形统计图如下图所示;
(2)解:(人),
估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生约人;
(3)解:由题意得,有名女生,名男生,
列表如下:
男 男 女 女 女
男 (男,男) (男,女) (男,女) (男,女)
男 (男,男) (男,女) (男,女) (男,女)
女 (女,男) (女,男) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女)
共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,
抽取的两名同学中恰好是一名女生和一名男生的概率为.
由条形统计图可知组有人,由扇形统计图可知组人数占总人数的,然后根据样本容量=频数÷百分数可计算出抽查的学生的总人数;再根据样本容量等于各小组频数之和可求得组的人数,根据组的人数,于是可将条形统计图补充完整;
根据条形统计图可知被抽查到的学生中参加家务劳动的时间在到分钟的人数共有人,占被抽查的总人数的,然后用样本估计总体可求解;
由题意,用列表法把所有可能出现的情况表示出来,共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,然后用概率公式计算即可求解.
(1)解:本次抽样的学生人数为(人),
组的人数为(人),
补全条形统计图如下图所示;
(2)解:(人),
估计该校九年级学生中参加家务劳动的时间在到分钟(含分钟)的学生约人;
(3)解:由题意得,有名女生,名男生,
列表如下:
男 男 女 女 女
男
(男,男) (男,女) (男,女) (男,女)
男 (男,男)
(男,女) (男,女) (男,女)
女 (女,男) (女,男)
(女,女) (女,女)
女 (女,男) (女,男) (女,女)
(女,女)
女 (女,男) (女,男) (女,女) (女,女)
共有种等可能的结果,其中抽取的两名同学中恰好是一名女生和一名男生的结果有种,
抽取的两名同学中恰好是一名女生和一名男生的概率为.
15.(1)解:∵一次函数 的图象过点.
解得
∴一次函数解析式为
∵与反比例函数 的图象过点.
解得
(2)解:由 (1) 知,
∴反比例函数解析式为
∵点B的横坐标为3,且点B在反比例函数图象上,
即
设点B向下平移了m个单位,
解得
∴向下平移的距离为
(1)把. )代入一次函数,反比例函数解析式即可求解;
(2)根据题意得到 根据点的平移得到平移后 代入一次函数解析式即可求解
16.(1)
(2)解:
(不合题意,舍去)
答:需将这批苹果存放35天后出售。
(3)
$
所以当时,最大,即存放45天后出售可获得最大利润,最大利润为4050元。
(1)根据苹果的单价乘以苹果的数量,可得函数关系式;
(2)根据利润等于销售总金额减去收购成本、减去每天的费用,可得方程,根据解方程,可得答案;
(3)根据利润等于销售总金额减去收购成本、减去每天的费用,可得二次函数,根据二次函数的性质,可得答案.
17.(1)∵当x=-1时,y=2+5-7=0,
∴二次函数图象经过点(-1,0),
∴二次函数y=2x2-5x-7是定点抛物线.
(2)由题意得,
∴
∴
(1) 把 1代入抛物线解析式,判断y的值是否为0,即可解决问题.
(2) 因为 与x轴只有一个公共点,所以 是抛物线顶点,所以抛物线解析式为 由此即可解决问题.
18.(1)解:①当时,,不合题意,舍去;
当时,,所以,符合合题意,
这时二次函数的表达式是;
当时,,所以,不合题意,舍去;
②因为二次函数的图象开口向上,对称轴是直线,
与y轴交于点(0,-3),
所以当x>1时,y随x的增大而增大,点(0,-3)关于直线x=1的对称点为(2,-3),
又当x≥m时,该函数的最小值是-3,
所以m=2.
(2)解:当x=n时,p=an2-2an-3;
当x=n+3时,q=a(n+3)2-2a(n+3)-3;
∴q=an2+4an+3a-3,
∴p-q=-6an-3a=-3a(2n+1)<0
∵a>0,
∴2n+1>0,解得:n>-0.5.
(1)①分别用x=2、x=1、x=-1代入函数解析式中,求出函数值,与相应的纵坐标比较后得出结论;
② 先根据二次函数解析式,求出对称轴,与y轴的交点,再结合增减性求得m的值;
(2)分别求出当x=n与x=n+3时的函数值,再根据列出关于n的不等式求解.
19.(1)解:甲机器人速度:30÷6=5(米/秒),
乙机器人速度:(70-7)÷18=3.5(米/秒),
甲机器人表演的时长为18-70÷5=18-14=4秒.
(2)解:当甲,乙机器人同时到达终点时,相遇点距离展展台终点的终点的距离为0;
当甲,乙机器人相遇在甲表演点时,70-30=40;
当甲,乙机器人相遇在甲表演点之前时,
乙机器人的函数表达式:y=+7,
甲机器人的函数表达式:y=5x(0≤x≤6);
当时,得,当,,
∴,
答:当甲、乙机器人相遇时,距离终点,40米或0米.
(1)先根据图象得出甲、乙机器人的路程和时间,再计算速度,然后计算出甲机器人表演的时长;
(2)结合图象分为“甲机器人表演前”、“表演时”、“到达终点时”三种情况,分别计算.
20.(1)a=4,b=20.
补全条形统计图如下:
(2)解:.
∴组所对应的圆心角度数为14.4°.
(3)解:0.4×480=192(人),
∴ 估计该校八年级学生的竞赛成绩在组的人数为192人.
解:(1)班级总人数为10÷20%=30,
∴b=50×40%=20,
∴a=50-2-14-20-10=4.
补全条形统计图如下:
(1)根据这一组的人数与所占百分比,可求得班级总人数,再根据这一组所占的百分比求得这一组的人数,然后利用求得班级总人数减去其他各组人数求得这一组人数,再补全条形统计图;
(2)根据A组的频数除以总数乘360度即可;
(3)根据D组所占百分比乘以八年级总人数即可.
21.解:,
将②代入①中得
.
解得.
将代入②,
得,.
∴原方程组的解为:.
观察原方程组可知,方程②中的x用含y的代数式表示出来,于是可将方程②代入方程①可得关于y的一元一次方程,解这个方程求出y的值,把y的值代入方程②求出x的值,再写出结论即可.
22.(1)解:本次调查的样本容量为:;
最喜欢“B足球”的学生人数为:人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为:
;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
(1)根据样本容量=频数÷百分数可得,样本容量=用最喜欢“D羽毛球”的学生人数除以其所占的百分比;根据各小组的频数之和等于样本容量可求出最喜欢“B足球”的学生人数,然后可将条形图补充完整;
(2)根据圆心角=360°×最喜欢“C排球”的学生人数所占的百分比计算即可求解;
(3)用样本估计总体即可求解.
(1)解:本次调查的样本容量是;
最喜欢“B足球”的学生人数为人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
23.的度数为
同课章节目录
