专项5 综合压轴题1 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用)
文档属性
| 名称 | 专项5 综合压轴题1 (浙江中考真题+中考模拟)【答案+解析】 ——2025年中考数学冲刺中考模拟真题速递(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 13:33:44 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)
专项5 综合压轴题1 (浙江中考真题+中考模拟)
一、综合题
1.(2024·金华真题)若干个工人装卸一批货物,每个工人的装卸速度相同。如果这些工人同时工作,则需10小时装卸完毕,现改变装卸方式,开始一个人干,以后每(整数)小时增加一个人干,每个参加装卸的人都一直干到装卸结束,且最后增加的一个人装卸的时间是第一个人装卸时间的.问:
(1)按改变后的装卸方式,自始至终需要多长时间
(2)参加装卸的有多少名工人
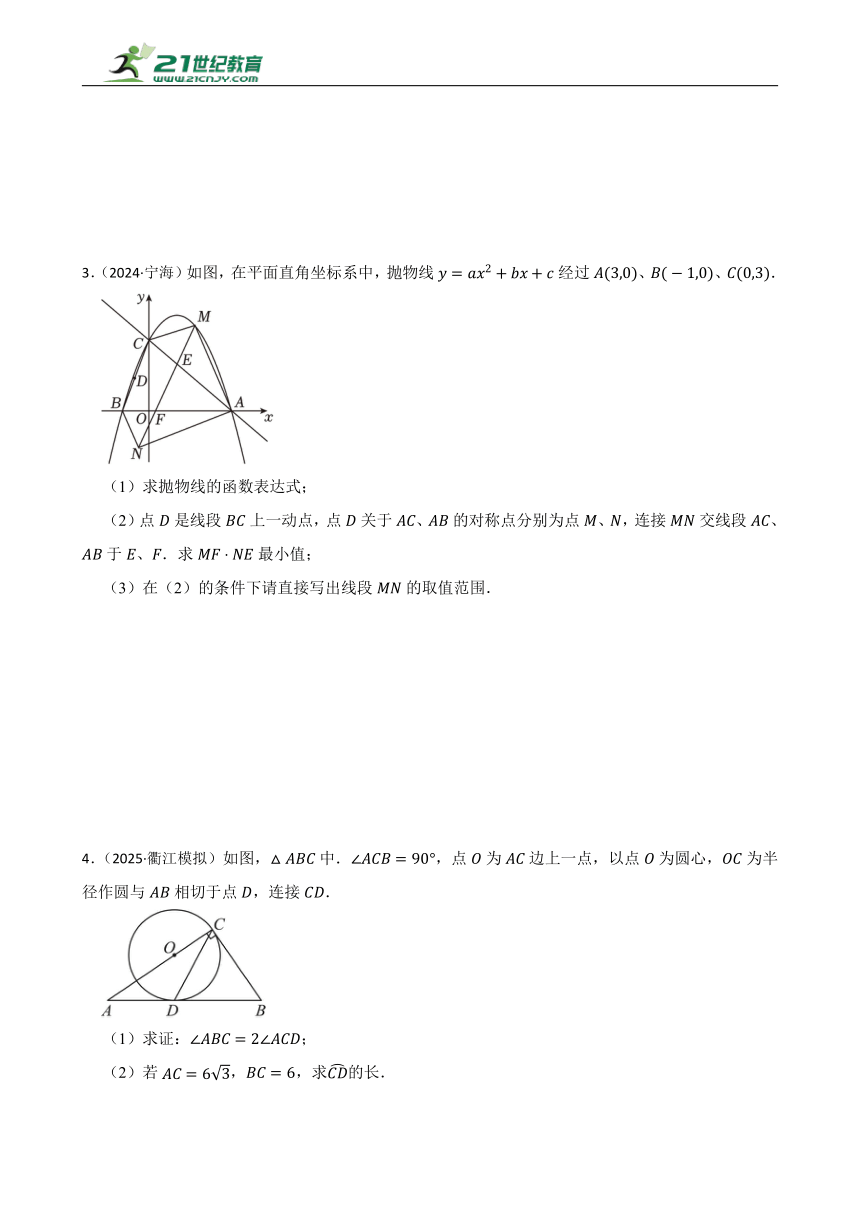
2.(2025·浙江模拟)已知AB为⊙O的直径,弦CD⊥AB于点E,连结BC.在AB上截取BF=BC,连结DF并延长,交⊙O于点G,连结CG.
(1)如图1,当点E与圆心O重合时,求∠D的度数.
(2)如图2,连结BG,交CD于点N,过点F作FM //BG,交CD于点M,连结GE.
①求证:BG平分∠ABC.
②若△EFG与△DFM的面积相等,BC=1,求BE的长.
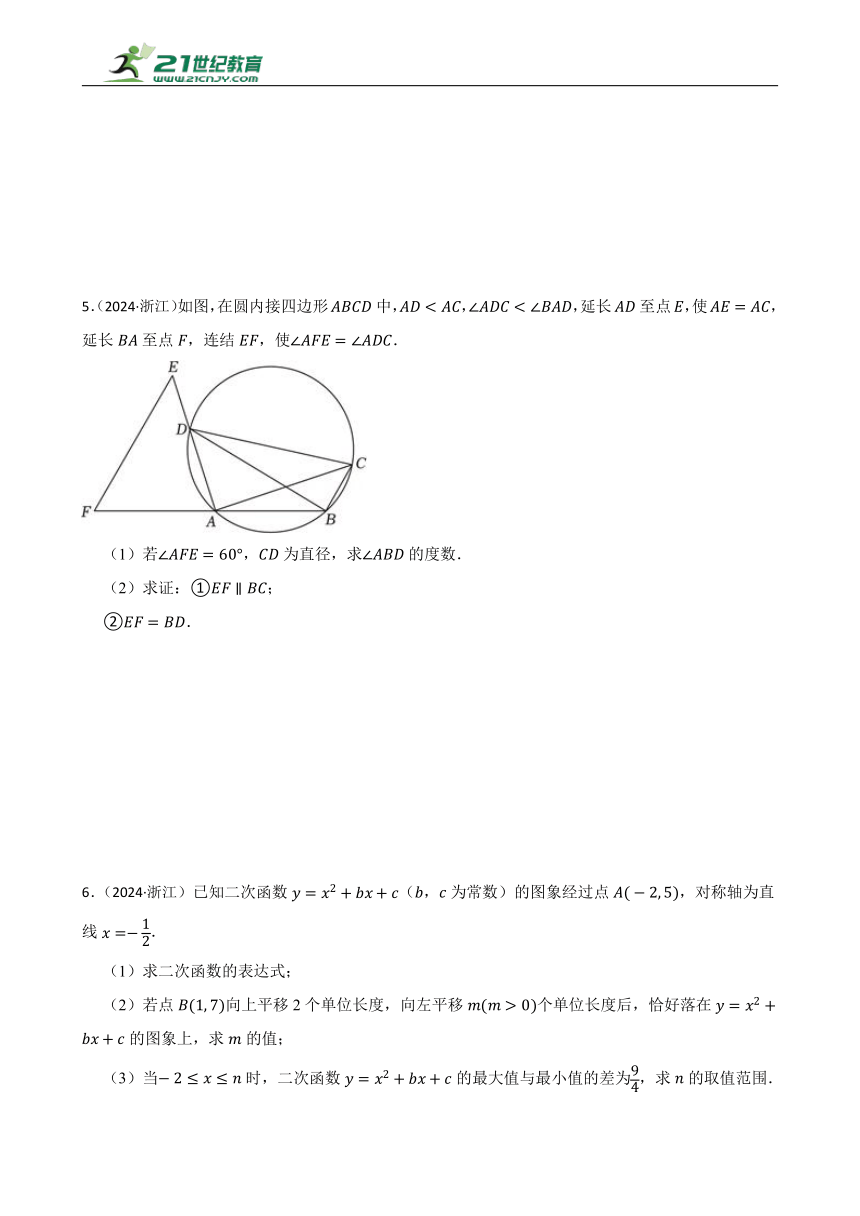
3.(2024·宁海)如图,在平面直角坐标系中,抛物线经过、、.
(1)求抛物线的函数表达式;
(2)点是线段上一动点,点关于、的对称点分别为点、,连接交线段、于、.求最小值;
(3)在(2)的条件下请直接写出线段的取值范围.
4.(2025·衢江模拟)如图,中.,点为边上一点,以点为圆心,为半径作圆与相切于点,连接.
(1)求证:;
(2)若,,求的长.
5.(2024·浙江)如图,在圆内接四边形中,,,延长至点,使,延长至点,连结,使.
(1)若,为直径,求的度数.
(2)求证:①;
②.
6.(2024·浙江)已知二次函数(,为常数)的图象经过点,对称轴为直线.
(1)求二次函数的表达式;
(2)若点向上平移2个单位长度,向左平移个单位长度后,恰好落在的图象上,求的值;
(3)当时,二次函数的最大值与最小值的差为,求的取值范围.
7.(2025九下·浙江模拟)如图1,是的直径,是圆上不同于的任意一点,延长到点,连结.过点作,交于点,连结.
(1)求证:.
(2)如图2,若,求的值.
(3)若,求的值(用含的代数式表示)
8.(2025九下·宁波模拟)如图1,四边形是的内接四边形,为对角线,且为的直径,,已知,.
(1)求的长;
(2)如图2,为上一点,过作,其反向延长线交于点,连结、、,若,
①求的值;
②试求的长.
9.(2025九下·浙江模拟)如图,在平面直角坐标系хOy中,一次函数y=x-1的图像与反比例函数y=的图像相交于点A(-1, a), B(b, 1)
(1)求反比例函数的表达式;
(2)连接OA、OB,求△OAB的面积.
10.(2025·浙江模拟)如图1,CD是⊙O的直径,弦AB⊥CD于点E,F是弧BC上一点,连结AC,CF,BF,AF,AF与CD交于点G。
(1)求证:∠AFC=∠CAB;
(2)如图2,连结CB交AF于点H。
①当AF⊥CB时,试判断△CGF的形状,并说明理由;
②在①的条件下,延长CF,AB相交于点Q,若CD=10,AB=8,求的值。
11.(2025·衢江模拟)无人机表演团队进行无人机表演训练,甲无人机从地面起飞,乙无人机从距离地面12米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,乙无人机继续匀速上升.当甲、乙无人机按照训练计划同时到达距离地面的高度为48米时,进行了时长为秒的联合表演,表演完成后以相同的速度同时返回地面.甲、乙两架无人机所在的位置距离地面的高度(米)与无人机飞行的时间(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)求联合表演时长;
(2)求线段所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们的高度差为8米?
12.(2025·温州模拟)如图,在圆内接四边形ABCD中,延长AB,DC交于点,在DE上方作,使点在线段DE上,且,连结DG.
(1)若为的中点,求的度数.
(2)连结BD,当时.
①求证:四边形BEGD是平行四边形.
②若,求证:.
13.(2025·衢州模拟)如图1,在Rt中,是的外接圆,点是的中点,连结CD交AB于点.
(1)求的度数.
(2)如图2,过点作,连结OD,若.
①若,求.
②连结OF,求OF的长.
14.(2025·衢江模拟)在矩形中,点,分别是,边上的动点,连接,交于点.
(1)如图(1),当点,分别是,的中点时,求证:;
(2)若,点是边上的点,连结交于点,点是的中点,
①如图(2),若,求的长;
②如图(3),连接,当,且时,求的值.
15.(2025·鹿城模拟)如图,内接于,连结交于点D,交于点E,已知.
(1)求证:;
(2)若,,求的长;
(3)若,设的半径为r,求的面积(用含r的代数式表示).
16.(2025·鹿城模拟)如图反映的是小温、小州两人从学校出发到瓯华站乘车的过程.两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留分钟后乘出租车赶往瓯华站,结果比小州早分钟到达瓯华站.
(1)求两人步行的速度.
(2)求出图中出租车行驶时路程与时间的函数解析式.
(3)求学校到瓯华站的路程.
17.(2025·钱塘模拟)在学习三角函数知识后,李老师布置了一项综合实践作业,要求利用所学知识测量建筑物的高度.如图,圆圆在自家楼顶处观测,测得对面一幢楼房顶部处的仰角为,测得这幢楼房底部处的俯角为.已知观测点处距地面的高度为24米(图中点均在同一平面内).
(1)求两幢楼房之间的水平距离(结果保留根号).
(2)求对面这幢楼房的高度(结果取整数).(参考数据:)
18.(2025·湖州模拟)已知甲、乙两地相距,小明、小红两人分别开车沿同一条公路从甲地出发到乙地,如图,线段,线段分别表示小明、小红离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)求小红离开甲地的路程与时间的函数表达式;
(2)当时间为何值时,都在行驶中的两人恰好相距.
19.(2025·浙江模拟)如图,⊙O是△ABC的外接圆,点D位于⊙O外一点,连接AD,BD,CD,BD交⊙O于点 E,连接CE.已知AB=AC=AD.
(1)如图1,求证:∠ACE=∠ADE.
(2)如图2,BD经过圆心O,AB=2CD.
①求 cos∠BAC 的值;
②若AB=3,求⊙O的半径,
20.(2025九下·浙江模拟)如图,为的直径,弦于,为弦上一点,且,射线与射线相交与点.
(1)求证:为的中点.
(2)①若,求的值.
②当为直角三角形时,求的正切值.
答案解析部分
1.(1)解:设装卸工作需要x小时完成,则第一人干了x小时,最后一个人干了小时,两人共干活小时,平均每人干活小时,根据题意可得:第二人与倒数第二人、第三人与倒数第三人,平均每人干活的时间也是小时,故可列方程为:,解得(小时)
(2)设共有y人参加装卸工作,又∵每(整数)小时增加一个人干,∴最后一人比第一人少干(y-1)t小时,根据题意可列方程:
,即,解此不定方程可得:,故参加人数y=2或3或4或5或7或13
2.(1)解:连接CF,
∵弦CD⊥AB于点E,
∴EC=ED
∴AB垂直平分CD,
∴FC=FD,
∵CD⊥AB,
∴∠CFE=∠DFE,
∵EC=EB,CD⊥AB,
∴∠B=∠ECB=45°,
∵BF=BC,
∴∠BFC=∠BCF =
=67.5°=∠BFD,
∴∠D=90°-67.5°= 22.5°;
(2)解:①证明:设∠1=α,连接CF,
∵CF=FD,
∴∠1=∠D.
∵∠4=∠D,
∴∠4=∠1=∠D=α.
∵CD⊥AB,
∴∠3=90°-∠1=90°-α.
∵BC=BF,
∴∠BCF=∠3=90°-α,
∴∠CBF=180°-∠BCF-∠3=180°-2(90°-α)=2α,
∴∠4=∠CBF,
∴BG平分∠ABC;
②连接CF与BG交于点H,连接AG,AC,作GP⊥AB,
∵BG平分∠ABC,
∴∠CBG=∠FBG,
∵BC=BF,BG=BG,
∴△ACBG≌△FBG(SAS),
∴GC=GF,∠CGB=∠FGB,
∵GH =GH
∴△HCG≌△HFG(SAS),
∴CH=FH,
∵FM//HN,
∴CH:CF=CN:CM,
∴CM=2CN,
∵OB⊥CD,
∴CD=2CE,
∴DM=CD-CM=2CE-2CN=2NE,
∵△EFG与△DFM的面积相等,
∴EF·GP=EF·DM,
∴GP=DM=2EN,
∵NE⊥AB,GP⊥AB,
∴NE//GP,
∴△BNE∽△BCP,
∴BE:BP=EN:GP=1:2,
设BE=PE=X,
∵BC=BF=1,
∴PF=2x-1,
∵∠GBC=GBA,
∴CG=AG=GF,
∵GP⊥AB,
∴AP=PF=2x-1,
∴AB=AF+BF=2PF+BF=4x-1,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴cos ∠ABC ==,
∴BC2=BE·AB,
∴4x2-x-1=0,
解得:x=(负值舍去),
∴BE=.
(1)连接CF,先证明AB垂直平分CD,根据垂直平分线的性质及在同一个三角形中等边对等角,可求得∠B=45°,再利用在同一个三角形中等边对等角,可求得∠BFC,然后根据直角三角形两个锐角互余,求得∠D;
(2)①设∠1=α,连接CF,先利用在同一个三角形中等边对等角,说明∠4=∠1=∠D=α,再利用在同一个三角形中等边对等角,说明∠BCF=∠3=90°-α,利用三角形内角和定理,可用α表示出∠CBF,从而可说明∠4=∠CBF,也就是BG平分∠ABC;
②设BE=PE=X,先利用SAS证明△ACBG≌△FBG,可用全等三角形的性质,得出GC=GF,∠CGB=∠FGB,再利用SAS证明SAS,可说明CH=FH,再根据FM//HN,列出比例式,说明CM=2CN,通过△EFG与△DFM的面积相等,说明GP=DM=2EN,再证明△BNE∽△BCP,列出比例式,得出PF=2x-1,然后借助余弦,说明BC2=BE·AB,可得出关于x的方程,求出x,正值即为BE的长.
3.(1)解:抛物线经过、、,
,
.
抛物线的函数表达式为;
(2)解:连接,,,如图,
点关于、的对称点分别为点、,
垂直平分,垂直平分,
,,
,.
,.
、、,
,.
.
,
为等腰直角三角形,
.
,,
,
,
,
,
点是线段上一动点,
当时,取得最小值,此时值最小.
当时,
,
.
,,
,
最小值为,
的最小值为
(3)解:(3)由(2)知:为等腰直角三角形,
,
,
.
点是线段上一动点,
点与点重合时,,点与点重合时,,
,
的最大值,
当时,取得最小值为,
的最大值,的最小值.
线段的取值范围为
(1)把三个点的坐标代入解析式得到三元一次方程组解题即可;
(2)连接AD, DM, DN, 可以得到 由 得到 则 为等腰直角三角形,再利用, 得到即可得到当时,取得最小值,此时值最小,然后利用面积法和勾股定理计算即可;
(3)利用 (2) 的结论得到根据AD的最小值与最大值解答即可得出结论.
4.(1)解:连接,则,
∵以点为圆心,为半径作圆与相切于点,
∴,
∴,
在Rt△OBD和Rt△OBC中
∴(HL),
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
由(1)知:,
∴,,
∴的长为:.
(1)连接,由题意,用HL定理可证,由全等三角形的对应边相等可得,∠OBC=∠OBD,于是可得垂直平分,根据同角的余角相等得即可求证;
(2)根据特殊角的三角函数值tan∠ABC=可求得,结合(1)的结论可得,根据锐角三角函数tan∠OBC=求出的长,然后用弧长公式L=计算即可求解.
(1)解:连接,则,
∵以点为圆心,为半径作圆与相切于点,
∴,
∴,
∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
由(1)知:,
∴,,
∴的长为:.
5.(1)解:∵CD是直径,
∴∠DBC=90°,
∵A四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=180°-60°=120°,
∴∠ABD=∠ABC-∠DBC=120°-90°=30°.
(2)①证明:①如图,延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC,
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF∥BC;
②过点D作DG∥BC交⊙O于点G,则DG∥BC∥EF,
∵DG∥BC,
∴,
∴BD=CG,
∵四边形BCGD是圆内接四边形,
∴∠GDE=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,
∴△AEF≌△ACG(AAS),
∴EF=CG,
∴EF=BD.
(1)利用直径所对的圆周角是直角,可证得∠DBC=90°,再利用圆内接四边形的对角互补,可求出∠ABC的度数;再根据∠ABD=∠ABC-∠DBC,代入计算可求出结果.
(2)①延长AB至M,利用圆内接四边形的性质可证得∠CBM=∠ADC=∠AFE,利用平行线的判定定理可证得结论;②②过点D作DG∥BC交⊙O于点G,连接CG,AG,则DG∥BC∥EF,可证得,利用圆心角、弧、弦的关系定理可证得BD=CG,利用圆内接四边形的对角互补及同弧所对的圆周角相等,可推出∠AFE=∠AGC,利用AAS证明△AEF≌△ACG,利用全等三角形的性质可证得EF=CG,据此可证得结论.
6.(1)解:由题意得
解之:
∴此二次函数解析式为y=x2+x+3
(2)解:∵ 点向上平移2个单位长度,向左平移个单位长度后,平移后的点的坐标为(1+m,9) ,
∵点(1-m,9)在二次函数图象上,
∴(1-m)2+(1-m)+3=9
解之:m1=4,m2=-1,
∵m>0,
∴m=4
(3)解:
∵抛物线的开口向上,
∴当时,y最小值=,
当时,y随x的增大而减小,
∴当x=-2时,y的最大值=4-2+3=5,
当x=n时,y的最小值为n2+n+3,
∵ 最大值与最小值的差为 ,
解之:(不符合题意);
当时,
当时,y最小值=,
当x=-2时,y的最大值=4-2+3=5,
∴最大值与最小值的差为5-=,符合题意;
若当x=n时,y的最大值为n2+n+3,
∵最大值与最小值的差为 ,
n2+n+3-=,
解之:n1=1,n2=-2(不符合题意),
综上所述n的值为1
(1)将点A的坐标代入,可得到关于b,c的方程,再利用抛物线的对称轴,可求出b的值,然后求出c的值,可得到二次函数解析式.
(2)利用点的坐标平移规律:上加下减,左减右加,可得到平移后的点的坐标,再将平移后的点的坐标代入函数解析式,可得到关于m的方程,解方程求出m的值,然后根据m>0,可得到m的值.
(3)将函数解析式转化为顶点式,利用二次函数的性质可知当时,y最小值=,当时,y随x的增大而减小;分情况讨论:当时,y随x的增大而减小,分别求出当x=-2时y的最大值和x=n时y的最小值,再根据最大值与最小值的差为 ,可得到关于n的方程,解方程求出n的值;当时,分别求出最大值和最小值,求出最大值与最小值的差;若当x=n时,y的最大值为n2+n+3,根据最大值与最小值的差为 ,可得到关于n的方程,解方程求出n的值;综上所述,可得到符合题意的n的值.
7.(1)证明: AB是⊙O的直径, C是圆上不同于A, B的任意一点, ,交BD于点E, 如图, 设CE, AB交点为G,
(2)解:
即
(3)解:过点E作 于点H,
设 则
在直角三角形ACG中,由勾股定理得:
即
即
(1)如图,设CE,AB交点为G,根据直径所对圆周角为 得到 由 得到 利用同角的余角相等即可证明结论;
(2)根据平行线的性质可证 证明 推出 求出BC,再证明 推出 求出CD,根据正切的定义即可求解;
(3)过点E作 于点H,根据 , 设 则 求出 证明 推出 即可得到求出 然后根据正切的定义解题即可.
8.(1)连结OD、OC,设OD与AC交于点P
∵AD=DC,∴,∴AC⊥OD,∴P为AC中点,
又O为圆心,AB为直径∴OP=BC=,
由S△ADC=S△ACB可知DP=BC=1,∴AB=3,从而AC=2
(2)①∵GF⊥AC,AG⊥BG,∠ACG=∠ABG
∴∠BAG=∠FGC,又∠CAB=∠CGB=∠AGF,
∴∠CAG=∠CGA,∴CG=AC=2.
设AF=a,由tan∠CAB=tan∠AGF=可知,
FG=2a,AG=3a,∴FC=2-a,
∴(2-a)2+(2a)2=(2)2,
解得a=,从而AG=,∴=.
②由△AFE∽△ACB,∴,
∴EF=,AE=,∴EG=FG-EF=,EB=
又由①得∠BCH=∠BAG=∠FGC,
∴△BCH∽△EGH,∴,解得BH=.
(1)连结OD、OC, 设OD与AC交于点P, 易得P为AC中点, 由 可知 进而利用勾股定理求解即可;
(2)①导角易求 设 易得 在 中利用勾股定理求解即可;
②易求 所以 证 即可得解.
9.(1)解:∵A(-1, a)在一次函数y=x-1的图象上,
∴a=-1-1=-2,
∴A(-1,-2)
又∵A(-1, -2)在反比例函数y=的图像,
∴m=-1×(-2)=2,
∴反比例函数的表达式为.
(2)解:∵点B (b, 1) 在一次函数y=x-1图象上,
∴b-1=1,解得b=2,
∴点B (2,1),
AB的直线表达式为y=x-1,
当y=0时,x-1=0,解得x=1,
∴AB与x轴交点(1,0),
∴ △OAB的面积 =.
(1)根据点A在一次函数图象上,求出a,再根据点A在反比例函数图象上,求出m,进而写出反比例函数表达式;
(2)
10.(1)证明:∵AB⊥CD,CD为⊙O的直径,
∴,
∴∠AFC=∠CAB.
(2)解: ①△CGF是等腰三角形.
∵AF⊥CB,CD⊥AB,
∴∠AEG=∠AHB=90°,
∴∠GAE+∠AGE=∠GAE+∠ABH=90°,
∴∠AGE=∠ABH,
∵∠AGE=∠CGF,∠AFC=∠ABH,
∴∠CGF=∠AFC,
∴CG=CF,
∴△CGF是等腰三角形.
②连结OA,AD,
∵AB⊥CD,CD为⊙O的直径,
∴AE=EB=4 , ,
∵CD=10,
∴OA=OC=OD=5,
在Rt△OAE中,OE==3,
∴DE=5-3=2,
在Rt△DAE中,AD== ,
∵△CGF是等腰三角形,CB⊥AF,
∴CH平分∠GCF,
∴∠FCH=∠GCH,
∵∠FCH=∠GAE,∠GCH=∠DAE,
∴∠DAE=∠GAE,
∵∠AEG=∠AED=90°,AE=AE,
∴△ADE≌△AGE(ASA),
∴DE=EG=2,
∴CG=10-2-2=6,
∴CF=6,
∵∠DAE=∠GAE
∴,
∴
∴BF=AD=,
∵∠BFQ=∠CAB,∠CAB=∠AFC,
∴∠BFQ=∠AFC,
∵∠FBQ=∠ACF,
∴△BFQ∽△CFA,
∴.
(1)先利用垂径定理证明=,再利用圆周角定理证明;
(2)①先判断△CGF是等腰三角形,再说理.先说明∠AGE=∠ABH,再∠CGF=∠AFC,然后根据等腰三角形判定得出结论;
②先利用勾股定理分别求得OE与AD,再利用等腰三角形三线合一,证得CH平分∠GCF,从而可得∠FCH=∠GCH,再利用ASA证明△ADE≌△AGE,分别求得CG、CF与BF,再证明△BFQ∽△CFA,列出比例式求得.
11.(1)解:由图可知:乙无人机的速度为:,
∴当乙无人机到达距离地面时,所用时间为:,
∴联合表演时长;
答:联合表演时长为;
(2)由(1)可知:,
联合表演前:甲无人机的速度为:,
设直线的解析式为:,
把代入,
得:,
解得:;
∴;
(3)由题意可分三种情况:
①当甲无人机单独表演之前:,解得:;
由(2)知:直线的解析式为:,
当时,,即:无人机甲从到,进而单独表演,
②当甲无人机单独表演时:时,;
③当甲无人机单独表演之后,时,;
综上可得:两架无人机表演训练到2秒,10秒和14秒时,它们的高度差为8米.
(1)求出乙无人机的速度,进而求出乙无人机到达距离地面的高度为48米时的时间,用表演完成时的时间减去开始表演的时间,求解即可;
(2)求出甲无人机的速度,结合点的坐标,待定系数法求出函数解析式即可;
(3)分甲单独表演之前和单独表演时和单独表演之后,三种情况进行讨论求解即可.
(1)解:由图可知:乙无人机的速度为:,
∴当乙无人机到达距离地面时,所用时间为:,
∴联合表演时长;
答:联合表演时长为;
(2)由(1)可知:,
联合表演前:甲无人机的速度为:,
设直线的解析式为:,把代入,得:,
解得:;
∴;
(3)①当甲无人机单独表演之前:,解得:;
由(2)知:直线的解析式为:,
当时,,即:无人机甲从到,进而单独表演,
②当甲无人机单独表演时:时,;
③当甲无人机单独表演之后,时,;
综上:两架无人机表演训练到2秒,10秒和14秒时,它们的高度差为8米.
12.(1)解:为的中点,.
,
.
,
.
(2)①,
,
.
,
,
四边形BEGD为平行四边形.
②如图2,过点作交圆于点,连结PD,
则,
.
四边形BEGD是平行四边形,
.
.
,
,
.
(1)由于圆内接四边形对角互补,因此求的度数,实质是求的度数;由于点平分劣弧,由圆周角定理知,等于等于,则由三角形内角和定理求出即可;
(2) ① 由圆周角定理知,等于等于,则由内错角相等两直线平行知,又因为,则由等角的补角相等可得到,则四边形BEGD是平行四边形;
② 可过点B作BP平行DE交圆于点P,此时由于夹在一组平行线间的圆弧相等,则BC等于PD;由圆周角定理结合平行线的性质可得等于,等于,由于平行四边形的对边相等即DB等于GE,则由“AAS”可证即可.
13.(1)解:∵AB是直径,
∴=180°,
∵点D是的中点,
∴=90°,
∴∠DCB=45°.
(2)①∵∠AOD=90°,tanD==,
∴设OE=a,
∴OD=2a,
∵AE=,OA=OD,
∴OE=OA-AE,
∴a=2a-,解得:a=.
∵AF⊥CD,
∴∠AFE=90°,
∵∠AEF=∠OED,
∴∠FAE=∠D,
∴tan∠FAE=,
∵tan∠FAE=,
∴,
∴EF=1,AF=2,
∵∠ACD=45°,
∴CF=AF=2,
∴CE=3,
∵DE2=OE2+OD2=25,
∴DE=5,
∴,
②当<时,
过点O作OG⊥CD,
∴,
∴EG=DE-DG=1,
∵EF=1∴GF=2,
∴△OEG~△OED,
∴,
∴OG=2,
∵OF2=OG2+GF2,
∴OF=
当>时
过点O作OG⊥CD,
∵∠BAF=∠D,
∴tanD=tan∠BAF,
∴设OE=b,OD=OA=2b,
∵AE=,
∴b=,
∴OE=,OD=OA=,
∴EF=1,AF=2,
∵∠OGB=∠AFE,∠OEG=∠AEF,
∴△OEG~△AEF,
∴,
∴OG=,
在Rt△ODG中,DG=,
在Rt△ODE中,DE=,
∴DF=,
∴GF=EF-(DE-DG)=
∴OF==.
综上所述,OF=或.
(1)先求得的度数,再求得的度数,然后求得;
(2)①先利用正切,设OE=a,可用a表示出OD,再利用线段差,得到关于a的方程求解,求得a,再求得tan∠FAE=,求得,从而求得EF与AF,再利用等腰直角三角形的性质求得CE,然后利用勾股定理求得DE,再求出CE与DE的比;
②分“<”、“>”两种情形,通过证明三角形相似,列出比例式,并用勾股定理分别求得OF.
14.(1)证明:连接交于点,
∵矩形,
∴,,,
∴,
∵点,分别是,的中点,
∴,则,
∴,
∴,
∴;
(2)解:①连接交于点,连接,
由(1)知,
∴,
∵,
∴,
∴,
∴,即,
∵点是的中点,点是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,即的长为2;
②设,则,
连接,,作于点,
则四边形是矩形,
∴,,
∴,
∴,
∵,,
∴,
∵点是的中点,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴.
(1)连接AC交BD于点O,根据矩形的性质可得,由三角形中位线的性质“三角形的中位线平行于第三边且等于第三边的一半”可得,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的性质“相似三角形的对应边的比相等”可得比例式即可求解;
(2)①连接交于点,连接,由三角形中位线定理求得,,再证明四边形是平行四边形,据此求解即可;
②设,则,连接,,作于点,求得,证明是线段的垂直平分线,求得,得到,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,根据相似三角形的性质“相似三角形的对应边的比相等”可得比例式求解.
(1)证明:连接交于点,
∵矩形,
∴,,,
∴,
∵点,分别是,的中点,
∴,则,
∴,
∴,
∴;
(2)解:①连接交于点,连接,
由(1)知,
∴,
∵,
∴,
∴,
∴,即,
∵点是的中点,点是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,即的长为2;
②设,则,连接,,作于点,
则四边形是矩形,
∴,,
∴,
∴,
∵,,
∴,
∵点是的中点,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴.
15.(1)证明:如图1,
∵是的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴;
(2)解:如图2,过点C作于M,
∵,,,
∴,
∴,
∴,
由勾股定理得:,
∵,,
∴,
∴,
∵,,,
∴,
∴;
(3)解:如图3,连接并延长交于F,连接,
∵,
∴,,
∴,
∴,,
由(2)知:,
∴,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
在中,,
∴,
设,则,
∵,
∴,
∴,
∵,
∴
.
答:三角形ABC的面积为.
(1)根据圆周角定理“同弧所对的圆周角等于它所对的圆心角的一半”可得,再由同角的余角可得,由等角对等边可得,最后由三角函数定义tan∠1=tan∠CAE=即可求证;
(2)如图2,过点C作于M,根据勾股定理可求得AE的值,由面积法可求得CM的值,在Rt△CDM中,用勾股定理求得EM的值,由等腰三角形的三线合一可得:,最后由圆周角定理和对顶角相等可得∠ADB=∠B,再根据等角对等边即可求解;
(3)如图3,连接并延长交于F,连接,先根据垂径定理得:,,根据三角形的内角和定理得:,则,是等腰直角三角形,设,则,由勾股定理和三角形的面积即可求解.
(1)证明:如图1,
∵是的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴;
(2)解:如图2,过点C作于M,
∵,,,
∴,
∴,
∴,
由勾股定理得:,
∵,,
∴,
∴,
∵,,,
∴,
∴;
(3)解:如图3,连接并延长交于F,连接,
∵,
∴,,
∴,
∴,,
由(2)知:,
∴,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
在中,,
∴,
设,则,
∵,
∴,
∴,
∵,
∴
.
16.(1)解:(米/分钟),
答:两人步行的速度是米/分钟;
(2)解:(分钟),
(米),
设与的函数解析式为(、为常数,且),
将坐标和分别代入,
得,
解得,
与的函数解析式为;
(3)解:设两人出发分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站.
,
解得,
当时,.
答:学校到瓯华站的路程是米.
(1)根据速度路程时间计算即可求解;
(2)由图中的信息可知图象经过点(12,0)和(16,1040),于是用待定系数法即可求解;
(3)设两人出发m分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站,根据两人分别到达终点时的路程相等列关于m的方程,解方程求出m的值,将m的值代入(1)中S与t的函数关系式计算即可求解.
(1)解:(米/分钟),
答:两人步行的速度是米/分钟;
(2)解:(分钟),
(米),
设与的函数解析式为(、为常数,且),
将坐标和分别代入,
得,
解得,
与的函数解析式为;
(3)解:设两人出发分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站.
,
解得,
当时,.
答:学校到瓯华站的路程是米.
17.(1)为米
(2)对面这幢楼房的高度约为米
18.(1)
(2)或
19.(1)证明:∵AB=AD,
∴∠ABD=∠ADB,
∵∠ACE=∠ABE,
∴∠ACE=∠ADE.
(2)解:①如图,连接AO,CO,
∵AO=BO=CO,
∴∠OBA=∠OAB=∠OAC=∠OCA,
∵AB=AC,
∴∠AOB=∠AOC.
∴∠OBA=∠OAB=∠BAC.
∵AC=AD,
∴∠ACD=∠ADC.
∵∠ACE=∠ADE,
∴∠ECD=∠EDC=∠BEC.
∵∠BAC=∠BEC,
∴∠OBA=∠OAB=∠ECD=∠EDC.
∴△ABO∽△CDE.
∵AB=2CD,
∴BO=2EC,
∴BE=4EC,
∵BD经过圆心O,
∴BD是⊙O的直径.
∴∠BCE=90°.
∴cos∠BAC=cos∠BEC=
(其他解法提示:如图3,连接AE并延长与CD相交于点G,
可证∠BAC=∠ACG,cos∠BAC=cos∠ACG=)
②如图,延长AO交BC于点F,
∵AB=AC,∠OAB=∠OAC,
∴AF⊥BC.
∴∠AFB=90°,BF=CF.
∵O为BE的中点,
∴FO=.
∵BO=AO=2CE,
∴BF2=BO2-FO2=CE2.
∴BF2=AB2-AF2=9-CE2.
∴CE2=.
∴CE=(舍去),CE=.
∴.
(1)先根据等边对等角,证明∠ABD=∠ADB, 再根据圆周角定理得出∠ACE=∠ABE,从而可得∠ACE=∠ADE.
(2)①先证明等边对等角,通过证明两对角分别相等,来证明△ABO∽△CDE,列出比例式,可证明BE=4EC, 再求出cos∠BAC;
②先证明AF⊥BC,利用中位线的定理可得FO=,再利用勾股定理可求得CE,从而可求得AO.
20.(1)证明:∵为的直径,,
∴,
∴,
∵,
∴,
∴,
∵为的直径,
∴,
,
,
∴,
∴,即为的中点;
(2)解:①,且,,
∴,
∴设,,
∴,
∵为的直径,,
∴,
∴,
∵,,
∴,
∴,
∴,
,
∴,
∴;
②∵射线与射线相交与点,
∴,
(i)如图,当时,,由(1)得,
,
设,
∴,
由(1)得,
∴,
;
(ii)如图,当时,,
,
∴四边形为平行四边形,
∵,
∴,
∴四边形为菱形,
∵,
∴四边形为正方形,
,
∴;
综上所述,的正切值为或1.
(1)根据垂径定理得,根据圆周角定理得,从而得,进而得,根据直径所对的圆周角是直角得,于是得,则有,即可得证结论;
(2)①根据,设,,利用勾股定理、垂径定理得,于是得,然后根据“母子”相似模型证出,从而得,进而求出,代入数据即可求;
②根据题意可知,然后两种情况讨论:(i)当时,先求出,设,得,从而得,进而得;(ii)当时,证出四边形为正方形,从而得,进而根据特殊角的三角函数值可知.
专项5 综合压轴题1 (浙江中考真题+中考模拟)
一、综合题
1.(2024·金华真题)若干个工人装卸一批货物,每个工人的装卸速度相同。如果这些工人同时工作,则需10小时装卸完毕,现改变装卸方式,开始一个人干,以后每(整数)小时增加一个人干,每个参加装卸的人都一直干到装卸结束,且最后增加的一个人装卸的时间是第一个人装卸时间的.问:
(1)按改变后的装卸方式,自始至终需要多长时间
(2)参加装卸的有多少名工人
2.(2025·浙江模拟)已知AB为⊙O的直径,弦CD⊥AB于点E,连结BC.在AB上截取BF=BC,连结DF并延长,交⊙O于点G,连结CG.
(1)如图1,当点E与圆心O重合时,求∠D的度数.
(2)如图2,连结BG,交CD于点N,过点F作FM //BG,交CD于点M,连结GE.
①求证:BG平分∠ABC.
②若△EFG与△DFM的面积相等,BC=1,求BE的长.
3.(2024·宁海)如图,在平面直角坐标系中,抛物线经过、、.
(1)求抛物线的函数表达式;
(2)点是线段上一动点,点关于、的对称点分别为点、,连接交线段、于、.求最小值;
(3)在(2)的条件下请直接写出线段的取值范围.
4.(2025·衢江模拟)如图,中.,点为边上一点,以点为圆心,为半径作圆与相切于点,连接.
(1)求证:;
(2)若,,求的长.
5.(2024·浙江)如图,在圆内接四边形中,,,延长至点,使,延长至点,连结,使.
(1)若,为直径,求的度数.
(2)求证:①;
②.
6.(2024·浙江)已知二次函数(,为常数)的图象经过点,对称轴为直线.
(1)求二次函数的表达式;
(2)若点向上平移2个单位长度,向左平移个单位长度后,恰好落在的图象上,求的值;
(3)当时,二次函数的最大值与最小值的差为,求的取值范围.
7.(2025九下·浙江模拟)如图1,是的直径,是圆上不同于的任意一点,延长到点,连结.过点作,交于点,连结.
(1)求证:.
(2)如图2,若,求的值.
(3)若,求的值(用含的代数式表示)
8.(2025九下·宁波模拟)如图1,四边形是的内接四边形,为对角线,且为的直径,,已知,.
(1)求的长;
(2)如图2,为上一点,过作,其反向延长线交于点,连结、、,若,
①求的值;
②试求的长.
9.(2025九下·浙江模拟)如图,在平面直角坐标系хOy中,一次函数y=x-1的图像与反比例函数y=的图像相交于点A(-1, a), B(b, 1)
(1)求反比例函数的表达式;
(2)连接OA、OB,求△OAB的面积.
10.(2025·浙江模拟)如图1,CD是⊙O的直径,弦AB⊥CD于点E,F是弧BC上一点,连结AC,CF,BF,AF,AF与CD交于点G。
(1)求证:∠AFC=∠CAB;
(2)如图2,连结CB交AF于点H。
①当AF⊥CB时,试判断△CGF的形状,并说明理由;
②在①的条件下,延长CF,AB相交于点Q,若CD=10,AB=8,求的值。
11.(2025·衢江模拟)无人机表演团队进行无人机表演训练,甲无人机从地面起飞,乙无人机从距离地面12米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,乙无人机继续匀速上升.当甲、乙无人机按照训练计划同时到达距离地面的高度为48米时,进行了时长为秒的联合表演,表演完成后以相同的速度同时返回地面.甲、乙两架无人机所在的位置距离地面的高度(米)与无人机飞行的时间(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)求联合表演时长;
(2)求线段所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们的高度差为8米?
12.(2025·温州模拟)如图,在圆内接四边形ABCD中,延长AB,DC交于点,在DE上方作,使点在线段DE上,且,连结DG.
(1)若为的中点,求的度数.
(2)连结BD,当时.
①求证:四边形BEGD是平行四边形.
②若,求证:.
13.(2025·衢州模拟)如图1,在Rt中,是的外接圆,点是的中点,连结CD交AB于点.
(1)求的度数.
(2)如图2,过点作,连结OD,若.
①若,求.
②连结OF,求OF的长.
14.(2025·衢江模拟)在矩形中,点,分别是,边上的动点,连接,交于点.
(1)如图(1),当点,分别是,的中点时,求证:;
(2)若,点是边上的点,连结交于点,点是的中点,
①如图(2),若,求的长;
②如图(3),连接,当,且时,求的值.
15.(2025·鹿城模拟)如图,内接于,连结交于点D,交于点E,已知.
(1)求证:;
(2)若,,求的长;
(3)若,设的半径为r,求的面积(用含r的代数式表示).
16.(2025·鹿城模拟)如图反映的是小温、小州两人从学校出发到瓯华站乘车的过程.两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留分钟后乘出租车赶往瓯华站,结果比小州早分钟到达瓯华站.
(1)求两人步行的速度.
(2)求出图中出租车行驶时路程与时间的函数解析式.
(3)求学校到瓯华站的路程.
17.(2025·钱塘模拟)在学习三角函数知识后,李老师布置了一项综合实践作业,要求利用所学知识测量建筑物的高度.如图,圆圆在自家楼顶处观测,测得对面一幢楼房顶部处的仰角为,测得这幢楼房底部处的俯角为.已知观测点处距地面的高度为24米(图中点均在同一平面内).
(1)求两幢楼房之间的水平距离(结果保留根号).
(2)求对面这幢楼房的高度(结果取整数).(参考数据:)
18.(2025·湖州模拟)已知甲、乙两地相距,小明、小红两人分别开车沿同一条公路从甲地出发到乙地,如图,线段,线段分别表示小明、小红离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)求小红离开甲地的路程与时间的函数表达式;
(2)当时间为何值时,都在行驶中的两人恰好相距.
19.(2025·浙江模拟)如图,⊙O是△ABC的外接圆,点D位于⊙O外一点,连接AD,BD,CD,BD交⊙O于点 E,连接CE.已知AB=AC=AD.
(1)如图1,求证:∠ACE=∠ADE.
(2)如图2,BD经过圆心O,AB=2CD.
①求 cos∠BAC 的值;
②若AB=3,求⊙O的半径,
20.(2025九下·浙江模拟)如图,为的直径,弦于,为弦上一点,且,射线与射线相交与点.
(1)求证:为的中点.
(2)①若,求的值.
②当为直角三角形时,求的正切值.
答案解析部分
1.(1)解:设装卸工作需要x小时完成,则第一人干了x小时,最后一个人干了小时,两人共干活小时,平均每人干活小时,根据题意可得:第二人与倒数第二人、第三人与倒数第三人,平均每人干活的时间也是小时,故可列方程为:,解得(小时)
(2)设共有y人参加装卸工作,又∵每(整数)小时增加一个人干,∴最后一人比第一人少干(y-1)t小时,根据题意可列方程:
,即,解此不定方程可得:,故参加人数y=2或3或4或5或7或13
2.(1)解:连接CF,
∵弦CD⊥AB于点E,
∴EC=ED
∴AB垂直平分CD,
∴FC=FD,
∵CD⊥AB,
∴∠CFE=∠DFE,
∵EC=EB,CD⊥AB,
∴∠B=∠ECB=45°,
∵BF=BC,
∴∠BFC=∠BCF =
=67.5°=∠BFD,
∴∠D=90°-67.5°= 22.5°;
(2)解:①证明:设∠1=α,连接CF,
∵CF=FD,
∴∠1=∠D.
∵∠4=∠D,
∴∠4=∠1=∠D=α.
∵CD⊥AB,
∴∠3=90°-∠1=90°-α.
∵BC=BF,
∴∠BCF=∠3=90°-α,
∴∠CBF=180°-∠BCF-∠3=180°-2(90°-α)=2α,
∴∠4=∠CBF,
∴BG平分∠ABC;
②连接CF与BG交于点H,连接AG,AC,作GP⊥AB,
∵BG平分∠ABC,
∴∠CBG=∠FBG,
∵BC=BF,BG=BG,
∴△ACBG≌△FBG(SAS),
∴GC=GF,∠CGB=∠FGB,
∵GH =GH
∴△HCG≌△HFG(SAS),
∴CH=FH,
∵FM//HN,
∴CH:CF=CN:CM,
∴CM=2CN,
∵OB⊥CD,
∴CD=2CE,
∴DM=CD-CM=2CE-2CN=2NE,
∵△EFG与△DFM的面积相等,
∴EF·GP=EF·DM,
∴GP=DM=2EN,
∵NE⊥AB,GP⊥AB,
∴NE//GP,
∴△BNE∽△BCP,
∴BE:BP=EN:GP=1:2,
设BE=PE=X,
∵BC=BF=1,
∴PF=2x-1,
∵∠GBC=GBA,
∴CG=AG=GF,
∵GP⊥AB,
∴AP=PF=2x-1,
∴AB=AF+BF=2PF+BF=4x-1,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴cos ∠ABC ==,
∴BC2=BE·AB,
∴4x2-x-1=0,
解得:x=(负值舍去),
∴BE=.
(1)连接CF,先证明AB垂直平分CD,根据垂直平分线的性质及在同一个三角形中等边对等角,可求得∠B=45°,再利用在同一个三角形中等边对等角,可求得∠BFC,然后根据直角三角形两个锐角互余,求得∠D;
(2)①设∠1=α,连接CF,先利用在同一个三角形中等边对等角,说明∠4=∠1=∠D=α,再利用在同一个三角形中等边对等角,说明∠BCF=∠3=90°-α,利用三角形内角和定理,可用α表示出∠CBF,从而可说明∠4=∠CBF,也就是BG平分∠ABC;
②设BE=PE=X,先利用SAS证明△ACBG≌△FBG,可用全等三角形的性质,得出GC=GF,∠CGB=∠FGB,再利用SAS证明SAS,可说明CH=FH,再根据FM//HN,列出比例式,说明CM=2CN,通过△EFG与△DFM的面积相等,说明GP=DM=2EN,再证明△BNE∽△BCP,列出比例式,得出PF=2x-1,然后借助余弦,说明BC2=BE·AB,可得出关于x的方程,求出x,正值即为BE的长.
3.(1)解:抛物线经过、、,
,
.
抛物线的函数表达式为;
(2)解:连接,,,如图,
点关于、的对称点分别为点、,
垂直平分,垂直平分,
,,
,.
,.
、、,
,.
.
,
为等腰直角三角形,
.
,,
,
,
,
,
点是线段上一动点,
当时,取得最小值,此时值最小.
当时,
,
.
,,
,
最小值为,
的最小值为
(3)解:(3)由(2)知:为等腰直角三角形,
,
,
.
点是线段上一动点,
点与点重合时,,点与点重合时,,
,
的最大值,
当时,取得最小值为,
的最大值,的最小值.
线段的取值范围为
(1)把三个点的坐标代入解析式得到三元一次方程组解题即可;
(2)连接AD, DM, DN, 可以得到 由 得到 则 为等腰直角三角形,再利用, 得到即可得到当时,取得最小值,此时值最小,然后利用面积法和勾股定理计算即可;
(3)利用 (2) 的结论得到根据AD的最小值与最大值解答即可得出结论.
4.(1)解:连接,则,
∵以点为圆心,为半径作圆与相切于点,
∴,
∴,
在Rt△OBD和Rt△OBC中
∴(HL),
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
由(1)知:,
∴,,
∴的长为:.
(1)连接,由题意,用HL定理可证,由全等三角形的对应边相等可得,∠OBC=∠OBD,于是可得垂直平分,根据同角的余角相等得即可求证;
(2)根据特殊角的三角函数值tan∠ABC=可求得,结合(1)的结论可得,根据锐角三角函数tan∠OBC=求出的长,然后用弧长公式L=计算即可求解.
(1)解:连接,则,
∵以点为圆心,为半径作圆与相切于点,
∴,
∴,
∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
由(1)知:,
∴,,
∴的长为:.
5.(1)解:∵CD是直径,
∴∠DBC=90°,
∵A四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=180°-60°=120°,
∴∠ABD=∠ABC-∠DBC=120°-90°=30°.
(2)①证明:①如图,延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC,
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF∥BC;
②过点D作DG∥BC交⊙O于点G,则DG∥BC∥EF,
∵DG∥BC,
∴,
∴BD=CG,
∵四边形BCGD是圆内接四边形,
∴∠GDE=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,
∴△AEF≌△ACG(AAS),
∴EF=CG,
∴EF=BD.
(1)利用直径所对的圆周角是直角,可证得∠DBC=90°,再利用圆内接四边形的对角互补,可求出∠ABC的度数;再根据∠ABD=∠ABC-∠DBC,代入计算可求出结果.
(2)①延长AB至M,利用圆内接四边形的性质可证得∠CBM=∠ADC=∠AFE,利用平行线的判定定理可证得结论;②②过点D作DG∥BC交⊙O于点G,连接CG,AG,则DG∥BC∥EF,可证得,利用圆心角、弧、弦的关系定理可证得BD=CG,利用圆内接四边形的对角互补及同弧所对的圆周角相等,可推出∠AFE=∠AGC,利用AAS证明△AEF≌△ACG,利用全等三角形的性质可证得EF=CG,据此可证得结论.
6.(1)解:由题意得
解之:
∴此二次函数解析式为y=x2+x+3
(2)解:∵ 点向上平移2个单位长度,向左平移个单位长度后,平移后的点的坐标为(1+m,9) ,
∵点(1-m,9)在二次函数图象上,
∴(1-m)2+(1-m)+3=9
解之:m1=4,m2=-1,
∵m>0,
∴m=4
(3)解:
∵抛物线的开口向上,
∴当时,y最小值=,
当时,y随x的增大而减小,
∴当x=-2时,y的最大值=4-2+3=5,
当x=n时,y的最小值为n2+n+3,
∵ 最大值与最小值的差为 ,
解之:(不符合题意);
当时,
当时,y最小值=,
当x=-2时,y的最大值=4-2+3=5,
∴最大值与最小值的差为5-=,符合题意;
若当x=n时,y的最大值为n2+n+3,
∵最大值与最小值的差为 ,
n2+n+3-=,
解之:n1=1,n2=-2(不符合题意),
综上所述n的值为1
(1)将点A的坐标代入,可得到关于b,c的方程,再利用抛物线的对称轴,可求出b的值,然后求出c的值,可得到二次函数解析式.
(2)利用点的坐标平移规律:上加下减,左减右加,可得到平移后的点的坐标,再将平移后的点的坐标代入函数解析式,可得到关于m的方程,解方程求出m的值,然后根据m>0,可得到m的值.
(3)将函数解析式转化为顶点式,利用二次函数的性质可知当时,y最小值=,当时,y随x的增大而减小;分情况讨论:当时,y随x的增大而减小,分别求出当x=-2时y的最大值和x=n时y的最小值,再根据最大值与最小值的差为 ,可得到关于n的方程,解方程求出n的值;当时,分别求出最大值和最小值,求出最大值与最小值的差;若当x=n时,y的最大值为n2+n+3,根据最大值与最小值的差为 ,可得到关于n的方程,解方程求出n的值;综上所述,可得到符合题意的n的值.
7.(1)证明: AB是⊙O的直径, C是圆上不同于A, B的任意一点, ,交BD于点E, 如图, 设CE, AB交点为G,
(2)解:
即
(3)解:过点E作 于点H,
设 则
在直角三角形ACG中,由勾股定理得:
即
即
(1)如图,设CE,AB交点为G,根据直径所对圆周角为 得到 由 得到 利用同角的余角相等即可证明结论;
(2)根据平行线的性质可证 证明 推出 求出BC,再证明 推出 求出CD,根据正切的定义即可求解;
(3)过点E作 于点H,根据 , 设 则 求出 证明 推出 即可得到求出 然后根据正切的定义解题即可.
8.(1)连结OD、OC,设OD与AC交于点P
∵AD=DC,∴,∴AC⊥OD,∴P为AC中点,
又O为圆心,AB为直径∴OP=BC=,
由S△ADC=S△ACB可知DP=BC=1,∴AB=3,从而AC=2
(2)①∵GF⊥AC,AG⊥BG,∠ACG=∠ABG
∴∠BAG=∠FGC,又∠CAB=∠CGB=∠AGF,
∴∠CAG=∠CGA,∴CG=AC=2.
设AF=a,由tan∠CAB=tan∠AGF=可知,
FG=2a,AG=3a,∴FC=2-a,
∴(2-a)2+(2a)2=(2)2,
解得a=,从而AG=,∴=.
②由△AFE∽△ACB,∴,
∴EF=,AE=,∴EG=FG-EF=,EB=
又由①得∠BCH=∠BAG=∠FGC,
∴△BCH∽△EGH,∴,解得BH=.
(1)连结OD、OC, 设OD与AC交于点P, 易得P为AC中点, 由 可知 进而利用勾股定理求解即可;
(2)①导角易求 设 易得 在 中利用勾股定理求解即可;
②易求 所以 证 即可得解.
9.(1)解:∵A(-1, a)在一次函数y=x-1的图象上,
∴a=-1-1=-2,
∴A(-1,-2)
又∵A(-1, -2)在反比例函数y=的图像,
∴m=-1×(-2)=2,
∴反比例函数的表达式为.
(2)解:∵点B (b, 1) 在一次函数y=x-1图象上,
∴b-1=1,解得b=2,
∴点B (2,1),
AB的直线表达式为y=x-1,
当y=0时,x-1=0,解得x=1,
∴AB与x轴交点(1,0),
∴ △OAB的面积 =.
(1)根据点A在一次函数图象上,求出a,再根据点A在反比例函数图象上,求出m,进而写出反比例函数表达式;
(2)
10.(1)证明:∵AB⊥CD,CD为⊙O的直径,
∴,
∴∠AFC=∠CAB.
(2)解: ①△CGF是等腰三角形.
∵AF⊥CB,CD⊥AB,
∴∠AEG=∠AHB=90°,
∴∠GAE+∠AGE=∠GAE+∠ABH=90°,
∴∠AGE=∠ABH,
∵∠AGE=∠CGF,∠AFC=∠ABH,
∴∠CGF=∠AFC,
∴CG=CF,
∴△CGF是等腰三角形.
②连结OA,AD,
∵AB⊥CD,CD为⊙O的直径,
∴AE=EB=4 , ,
∵CD=10,
∴OA=OC=OD=5,
在Rt△OAE中,OE==3,
∴DE=5-3=2,
在Rt△DAE中,AD== ,
∵△CGF是等腰三角形,CB⊥AF,
∴CH平分∠GCF,
∴∠FCH=∠GCH,
∵∠FCH=∠GAE,∠GCH=∠DAE,
∴∠DAE=∠GAE,
∵∠AEG=∠AED=90°,AE=AE,
∴△ADE≌△AGE(ASA),
∴DE=EG=2,
∴CG=10-2-2=6,
∴CF=6,
∵∠DAE=∠GAE
∴,
∴
∴BF=AD=,
∵∠BFQ=∠CAB,∠CAB=∠AFC,
∴∠BFQ=∠AFC,
∵∠FBQ=∠ACF,
∴△BFQ∽△CFA,
∴.
(1)先利用垂径定理证明=,再利用圆周角定理证明;
(2)①先判断△CGF是等腰三角形,再说理.先说明∠AGE=∠ABH,再∠CGF=∠AFC,然后根据等腰三角形判定得出结论;
②先利用勾股定理分别求得OE与AD,再利用等腰三角形三线合一,证得CH平分∠GCF,从而可得∠FCH=∠GCH,再利用ASA证明△ADE≌△AGE,分别求得CG、CF与BF,再证明△BFQ∽△CFA,列出比例式求得.
11.(1)解:由图可知:乙无人机的速度为:,
∴当乙无人机到达距离地面时,所用时间为:,
∴联合表演时长;
答:联合表演时长为;
(2)由(1)可知:,
联合表演前:甲无人机的速度为:,
设直线的解析式为:,
把代入,
得:,
解得:;
∴;
(3)由题意可分三种情况:
①当甲无人机单独表演之前:,解得:;
由(2)知:直线的解析式为:,
当时,,即:无人机甲从到,进而单独表演,
②当甲无人机单独表演时:时,;
③当甲无人机单独表演之后,时,;
综上可得:两架无人机表演训练到2秒,10秒和14秒时,它们的高度差为8米.
(1)求出乙无人机的速度,进而求出乙无人机到达距离地面的高度为48米时的时间,用表演完成时的时间减去开始表演的时间,求解即可;
(2)求出甲无人机的速度,结合点的坐标,待定系数法求出函数解析式即可;
(3)分甲单独表演之前和单独表演时和单独表演之后,三种情况进行讨论求解即可.
(1)解:由图可知:乙无人机的速度为:,
∴当乙无人机到达距离地面时,所用时间为:,
∴联合表演时长;
答:联合表演时长为;
(2)由(1)可知:,
联合表演前:甲无人机的速度为:,
设直线的解析式为:,把代入,得:,
解得:;
∴;
(3)①当甲无人机单独表演之前:,解得:;
由(2)知:直线的解析式为:,
当时,,即:无人机甲从到,进而单独表演,
②当甲无人机单独表演时:时,;
③当甲无人机单独表演之后,时,;
综上:两架无人机表演训练到2秒,10秒和14秒时,它们的高度差为8米.
12.(1)解:为的中点,.
,
.
,
.
(2)①,
,
.
,
,
四边形BEGD为平行四边形.
②如图2,过点作交圆于点,连结PD,
则,
.
四边形BEGD是平行四边形,
.
.
,
,
.
(1)由于圆内接四边形对角互补,因此求的度数,实质是求的度数;由于点平分劣弧,由圆周角定理知,等于等于,则由三角形内角和定理求出即可;
(2) ① 由圆周角定理知,等于等于,则由内错角相等两直线平行知,又因为,则由等角的补角相等可得到,则四边形BEGD是平行四边形;
② 可过点B作BP平行DE交圆于点P,此时由于夹在一组平行线间的圆弧相等,则BC等于PD;由圆周角定理结合平行线的性质可得等于,等于,由于平行四边形的对边相等即DB等于GE,则由“AAS”可证即可.
13.(1)解:∵AB是直径,
∴=180°,
∵点D是的中点,
∴=90°,
∴∠DCB=45°.
(2)①∵∠AOD=90°,tanD==,
∴设OE=a,
∴OD=2a,
∵AE=,OA=OD,
∴OE=OA-AE,
∴a=2a-,解得:a=.
∵AF⊥CD,
∴∠AFE=90°,
∵∠AEF=∠OED,
∴∠FAE=∠D,
∴tan∠FAE=,
∵tan∠FAE=,
∴,
∴EF=1,AF=2,
∵∠ACD=45°,
∴CF=AF=2,
∴CE=3,
∵DE2=OE2+OD2=25,
∴DE=5,
∴,
②当<时,
过点O作OG⊥CD,
∴,
∴EG=DE-DG=1,
∵EF=1∴GF=2,
∴△OEG~△OED,
∴,
∴OG=2,
∵OF2=OG2+GF2,
∴OF=
当>时
过点O作OG⊥CD,
∵∠BAF=∠D,
∴tanD=tan∠BAF,
∴设OE=b,OD=OA=2b,
∵AE=,
∴b=,
∴OE=,OD=OA=,
∴EF=1,AF=2,
∵∠OGB=∠AFE,∠OEG=∠AEF,
∴△OEG~△AEF,
∴,
∴OG=,
在Rt△ODG中,DG=,
在Rt△ODE中,DE=,
∴DF=,
∴GF=EF-(DE-DG)=
∴OF==.
综上所述,OF=或.
(1)先求得的度数,再求得的度数,然后求得;
(2)①先利用正切,设OE=a,可用a表示出OD,再利用线段差,得到关于a的方程求解,求得a,再求得tan∠FAE=,求得,从而求得EF与AF,再利用等腰直角三角形的性质求得CE,然后利用勾股定理求得DE,再求出CE与DE的比;
②分“<”、“>”两种情形,通过证明三角形相似,列出比例式,并用勾股定理分别求得OF.
14.(1)证明:连接交于点,
∵矩形,
∴,,,
∴,
∵点,分别是,的中点,
∴,则,
∴,
∴,
∴;
(2)解:①连接交于点,连接,
由(1)知,
∴,
∵,
∴,
∴,
∴,即,
∵点是的中点,点是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,即的长为2;
②设,则,
连接,,作于点,
则四边形是矩形,
∴,,
∴,
∴,
∵,,
∴,
∵点是的中点,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴.
(1)连接AC交BD于点O,根据矩形的性质可得,由三角形中位线的性质“三角形的中位线平行于第三边且等于第三边的一半”可得,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,由相似三角形的性质“相似三角形的对应边的比相等”可得比例式即可求解;
(2)①连接交于点,连接,由三角形中位线定理求得,,再证明四边形是平行四边形,据此求解即可;
②设,则,连接,,作于点,求得,证明是线段的垂直平分线,求得,得到,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得,根据相似三角形的性质“相似三角形的对应边的比相等”可得比例式求解.
(1)证明:连接交于点,
∵矩形,
∴,,,
∴,
∵点,分别是,的中点,
∴,则,
∴,
∴,
∴;
(2)解:①连接交于点,连接,
由(1)知,
∴,
∵,
∴,
∴,
∴,即,
∵点是的中点,点是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,即的长为2;
②设,则,连接,,作于点,
则四边形是矩形,
∴,,
∴,
∴,
∵,,
∴,
∵点是的中点,
∴是线段的垂直平分线,
∴,
∴,
∵,
∴,
∴,
∴.
15.(1)证明:如图1,
∵是的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴;
(2)解:如图2,过点C作于M,
∵,,,
∴,
∴,
∴,
由勾股定理得:,
∵,,
∴,
∴,
∵,,,
∴,
∴;
(3)解:如图3,连接并延长交于F,连接,
∵,
∴,,
∴,
∴,,
由(2)知:,
∴,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
在中,,
∴,
设,则,
∵,
∴,
∴,
∵,
∴
.
答:三角形ABC的面积为.
(1)根据圆周角定理“同弧所对的圆周角等于它所对的圆心角的一半”可得,再由同角的余角可得,由等角对等边可得,最后由三角函数定义tan∠1=tan∠CAE=即可求证;
(2)如图2,过点C作于M,根据勾股定理可求得AE的值,由面积法可求得CM的值,在Rt△CDM中,用勾股定理求得EM的值,由等腰三角形的三线合一可得:,最后由圆周角定理和对顶角相等可得∠ADB=∠B,再根据等角对等边即可求解;
(3)如图3,连接并延长交于F,连接,先根据垂径定理得:,,根据三角形的内角和定理得:,则,是等腰直角三角形,设,则,由勾股定理和三角形的面积即可求解.
(1)证明:如图1,
∵是的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴;
(2)解:如图2,过点C作于M,
∵,,,
∴,
∴,
∴,
由勾股定理得:,
∵,,
∴,
∴,
∵,,,
∴,
∴;
(3)解:如图3,连接并延长交于F,连接,
∵,
∴,,
∴,
∴,,
由(2)知:,
∴,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
在中,,
∴,
设,则,
∵,
∴,
∴,
∵,
∴
.
16.(1)解:(米/分钟),
答:两人步行的速度是米/分钟;
(2)解:(分钟),
(米),
设与的函数解析式为(、为常数,且),
将坐标和分别代入,
得,
解得,
与的函数解析式为;
(3)解:设两人出发分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站.
,
解得,
当时,.
答:学校到瓯华站的路程是米.
(1)根据速度路程时间计算即可求解;
(2)由图中的信息可知图象经过点(12,0)和(16,1040),于是用待定系数法即可求解;
(3)设两人出发m分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站,根据两人分别到达终点时的路程相等列关于m的方程,解方程求出m的值,将m的值代入(1)中S与t的函数关系式计算即可求解.
(1)解:(米/分钟),
答:两人步行的速度是米/分钟;
(2)解:(分钟),
(米),
设与的函数解析式为(、为常数,且),
将坐标和分别代入,
得,
解得,
与的函数解析式为;
(3)解:设两人出发分钟时小温到达瓯华站,则两人出发分钟时小州到达瓯华站.
,
解得,
当时,.
答:学校到瓯华站的路程是米.
17.(1)为米
(2)对面这幢楼房的高度约为米
18.(1)
(2)或
19.(1)证明:∵AB=AD,
∴∠ABD=∠ADB,
∵∠ACE=∠ABE,
∴∠ACE=∠ADE.
(2)解:①如图,连接AO,CO,
∵AO=BO=CO,
∴∠OBA=∠OAB=∠OAC=∠OCA,
∵AB=AC,
∴∠AOB=∠AOC.
∴∠OBA=∠OAB=∠BAC.
∵AC=AD,
∴∠ACD=∠ADC.
∵∠ACE=∠ADE,
∴∠ECD=∠EDC=∠BEC.
∵∠BAC=∠BEC,
∴∠OBA=∠OAB=∠ECD=∠EDC.
∴△ABO∽△CDE.
∵AB=2CD,
∴BO=2EC,
∴BE=4EC,
∵BD经过圆心O,
∴BD是⊙O的直径.
∴∠BCE=90°.
∴cos∠BAC=cos∠BEC=
(其他解法提示:如图3,连接AE并延长与CD相交于点G,
可证∠BAC=∠ACG,cos∠BAC=cos∠ACG=)
②如图,延长AO交BC于点F,
∵AB=AC,∠OAB=∠OAC,
∴AF⊥BC.
∴∠AFB=90°,BF=CF.
∵O为BE的中点,
∴FO=.
∵BO=AO=2CE,
∴BF2=BO2-FO2=CE2.
∴BF2=AB2-AF2=9-CE2.
∴CE2=.
∴CE=(舍去),CE=.
∴.
(1)先根据等边对等角,证明∠ABD=∠ADB, 再根据圆周角定理得出∠ACE=∠ABE,从而可得∠ACE=∠ADE.
(2)①先证明等边对等角,通过证明两对角分别相等,来证明△ABO∽△CDE,列出比例式,可证明BE=4EC, 再求出cos∠BAC;
②先证明AF⊥BC,利用中位线的定理可得FO=,再利用勾股定理可求得CE,从而可求得AO.
20.(1)证明:∵为的直径,,
∴,
∴,
∵,
∴,
∴,
∵为的直径,
∴,
,
,
∴,
∴,即为的中点;
(2)解:①,且,,
∴,
∴设,,
∴,
∵为的直径,,
∴,
∴,
∵,,
∴,
∴,
∴,
,
∴,
∴;
②∵射线与射线相交与点,
∴,
(i)如图,当时,,由(1)得,
,
设,
∴,
由(1)得,
∴,
;
(ii)如图,当时,,
,
∴四边形为平行四边形,
∵,
∴,
∴四边形为菱形,
∵,
∴四边形为正方形,
,
∴;
综上所述,的正切值为或1.
(1)根据垂径定理得,根据圆周角定理得,从而得,进而得,根据直径所对的圆周角是直角得,于是得,则有,即可得证结论;
(2)①根据,设,,利用勾股定理、垂径定理得,于是得,然后根据“母子”相似模型证出,从而得,进而求出,代入数据即可求;
②根据题意可知,然后两种情况讨论:(i)当时,先求出,设,得,从而得,进而得;(ii)当时,证出四边形为正方形,从而得,进而根据特殊角的三角函数值可知.
同课章节目录
