2025年中考数学二轮复习 专题10 与圆周角相关的计算 课件(共17张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习 专题10 与圆周角相关的计算 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 606.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 07:29:05 | ||
图片预览




文档简介
(共17张PPT)
专题十 与圆周角相关的计算
类型一 90°的圆周角
如图,“直径”或“半圆”→90°圆周角→直角三角形→关联
计算.
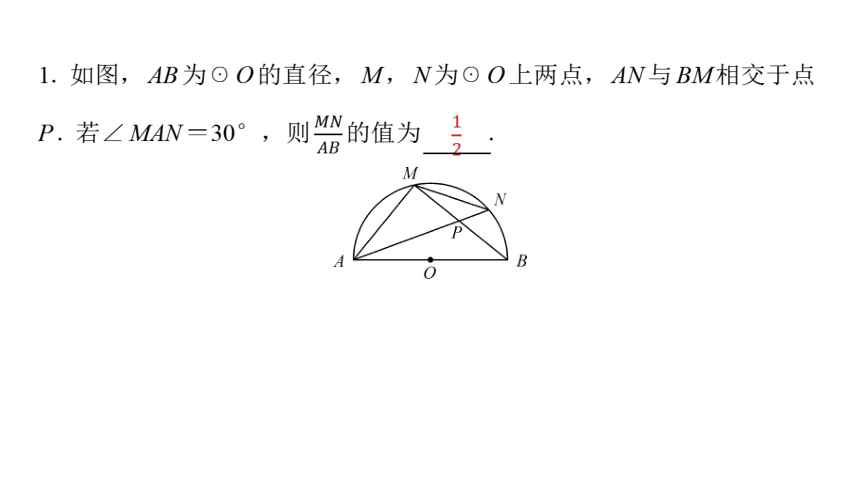
1. 如图,AB为☉O的直径,M,N为☉O上两点,AN与BM相交于点
P. 若∠MAN=30°,则 的值为 .
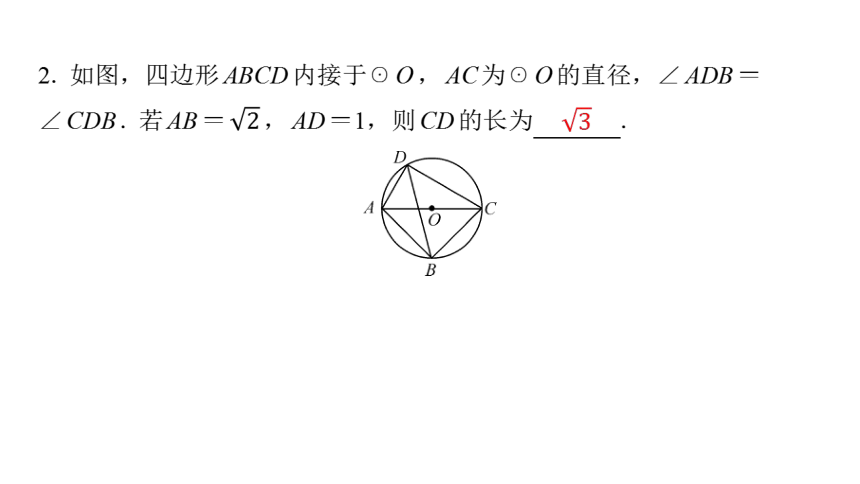
2. 如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=
∠CDB. 若AB= ,AD=1,则CD的长为 .
3. 如图,在边长为1的正方形网格中,☉O是△ABC的外接圆,点A,
B,O在格点上,则 cos ∠ACB的值是 .
4. 如图,在△ABC中,AB=AC,以AB为直径的☉O分别交BC,AC
于点D,E,连接DE. 若DE= ,AB=10,则AE的长为 .
8
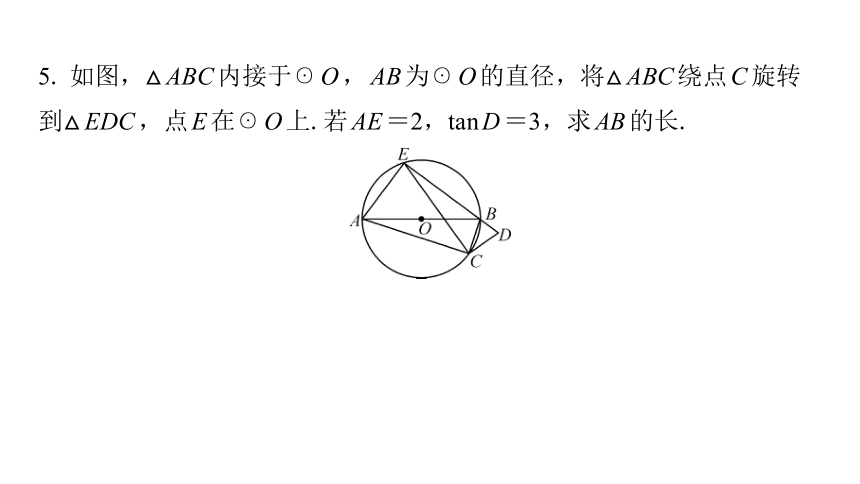
5. 如图,△ABC内接于☉O,AB为☉O的直径,将△ABC绕点C旋转
到△EDC,点E在☉O上.若AE=2,tanD=3,求AB的长.
解:∵AB为☉O的直径,∴∠AEB=∠ACB=∠ECD=90°.
∵tanD= =3,∴设CD=x,CE=3x,则AB=DE= x.
∵ = ,∠ACE=∠BCD,∴△ACE∽△BCD,
∴ = =3,∴ =3,BD= ,∴BE=DE-BD= x- .
∵AE2+BE2=AB2,∴22+ = ,解得x=
,∴AB= x= .
类型二 45°的圆周角
如图,“半圆中点”或“45°圆周角”→90°圆心角→等腰直角
三角形→关联计算.
1. 如图,正方形ABCD内接于☉O,在 上取一点E,连接AE,作
AG⊥AE,交☉O于点G,连接DG. 若AB=2,∠BAE=30°,求AG
的长.
解:如图,连接OA,OD,OG,过点D作DM⊥AG于点M.∵四边形ABCD为☉O的内接正方形,
∴∠AOD=90°,∠AGD= ∠AOD=45°,∴OD= AD= ×2
= .
∵∠EAG=∠BAD=90°,∴∠GAD=∠BAE=30°,∴∠GOD=
2∠GAD=60°,
∴△ODG是等边三角形,∴DG=OD= ,∴DM=GM= DG=
× =1,
∴AM= = = ,∴AG=AM+GM= +1.
2. 如图,在☉O中,AB,CD是互相垂直的两条直径,点E在
上,CF⊥AE于点F. 若F是弦AE的三等分点,☉O 的直径为12,求
CF的长.
解:如图,连接AC,CE. ∵CD⊥AB,∴∠AEC=∠AOC=45°,
∴△FCE是等腰直角三角形.设CF=EF=a,则AF=2a.
∵☉O 的直径为12,∴AC= OA=6 .
∵AC2=AF2+CF2,∴ =(2a)2+a2,
解得a1= ,a2=- (舍去),∴CF= .
3. 如图,AB为半圆O的直径,C为 的中点,点D在半圆上,BD=
6,AB=10,求CD的长.
解:如图,连接AD,OC,过点C作CE⊥AD于点E.
∵AB为半圆O的直径,
∴∠ADB=90°,∴AD= = =8.
∵C为 的中点,∴∠AOC=90°,∴AC= OA=5 ,
∴∠ADC= ∠AOC=45°,∴CE=DE.
设CE=DE=a,则AE=8-a.∵AC2=AE2+CE2,
∴ =(8-a)2+a2,解得a1=1,a2=7(舍去),
∴CE=DE=1,∴CD= CE= .
谢谢观看
专题十 与圆周角相关的计算
类型一 90°的圆周角
如图,“直径”或“半圆”→90°圆周角→直角三角形→关联
计算.
1. 如图,AB为☉O的直径,M,N为☉O上两点,AN与BM相交于点
P. 若∠MAN=30°,则 的值为 .
2. 如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=
∠CDB. 若AB= ,AD=1,则CD的长为 .
3. 如图,在边长为1的正方形网格中,☉O是△ABC的外接圆,点A,
B,O在格点上,则 cos ∠ACB的值是 .
4. 如图,在△ABC中,AB=AC,以AB为直径的☉O分别交BC,AC
于点D,E,连接DE. 若DE= ,AB=10,则AE的长为 .
8
5. 如图,△ABC内接于☉O,AB为☉O的直径,将△ABC绕点C旋转
到△EDC,点E在☉O上.若AE=2,tanD=3,求AB的长.
解:∵AB为☉O的直径,∴∠AEB=∠ACB=∠ECD=90°.
∵tanD= =3,∴设CD=x,CE=3x,则AB=DE= x.
∵ = ,∠ACE=∠BCD,∴△ACE∽△BCD,
∴ = =3,∴ =3,BD= ,∴BE=DE-BD= x- .
∵AE2+BE2=AB2,∴22+ = ,解得x=
,∴AB= x= .
类型二 45°的圆周角
如图,“半圆中点”或“45°圆周角”→90°圆心角→等腰直角
三角形→关联计算.
1. 如图,正方形ABCD内接于☉O,在 上取一点E,连接AE,作
AG⊥AE,交☉O于点G,连接DG. 若AB=2,∠BAE=30°,求AG
的长.
解:如图,连接OA,OD,OG,过点D作DM⊥AG于点M.∵四边形ABCD为☉O的内接正方形,
∴∠AOD=90°,∠AGD= ∠AOD=45°,∴OD= AD= ×2
= .
∵∠EAG=∠BAD=90°,∴∠GAD=∠BAE=30°,∴∠GOD=
2∠GAD=60°,
∴△ODG是等边三角形,∴DG=OD= ,∴DM=GM= DG=
× =1,
∴AM= = = ,∴AG=AM+GM= +1.
2. 如图,在☉O中,AB,CD是互相垂直的两条直径,点E在
上,CF⊥AE于点F. 若F是弦AE的三等分点,☉O 的直径为12,求
CF的长.
解:如图,连接AC,CE. ∵CD⊥AB,∴∠AEC=∠AOC=45°,
∴△FCE是等腰直角三角形.设CF=EF=a,则AF=2a.
∵☉O 的直径为12,∴AC= OA=6 .
∵AC2=AF2+CF2,∴ =(2a)2+a2,
解得a1= ,a2=- (舍去),∴CF= .
3. 如图,AB为半圆O的直径,C为 的中点,点D在半圆上,BD=
6,AB=10,求CD的长.
解:如图,连接AD,OC,过点C作CE⊥AD于点E.
∵AB为半圆O的直径,
∴∠ADB=90°,∴AD= = =8.
∵C为 的中点,∴∠AOC=90°,∴AC= OA=5 ,
∴∠ADC= ∠AOC=45°,∴CE=DE.
设CE=DE=a,则AE=8-a.∵AC2=AE2+CE2,
∴ =(8-a)2+a2,解得a1=1,a2=7(舍去),
∴CE=DE=1,∴CD= CE= .
谢谢观看
同课章节目录
