人教版八年级下册数学 第十七章 勾股定理 单元测试题(含答案)
文档属性
| 名称 | 人教版八年级下册数学 第十七章 勾股定理 单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1017.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 16:39:31 | ||
图片预览




文档简介
八年级数学新人教版下册第十七章《勾股定理》单元测试题
一、单选题
1.如图,在Rt ABC中,,点在的延长线上,且,则的长是( )
A. B. C. D.
2.满足下列条件的 ABC中,不是直角三角形的是( )
A. B.,,
C. D.
3.如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
A. B. C. D.
4.如图,某自动感应门的正上方装着一个感应器A,离地距离,当人体进入感应范围内时,感应门就会自动打开,一个身高的学生刚走到离门间距的地方时,感应门自动打开,则该感应器感应长度为( )
A. B. C. D.
5.如图,,以为直角边作,使,再以为直角边作,使,,依此法继续作下去,则的长为( )
A. B. C. D.
6.如图,在中,,,,点为边的中点,点E在边上,且,则的长为( )
A.2 B. C. D.3
7.在 ABC中,,为边上的中线,,平分外角,过作交于点,则的长为( )
A.6 B.7 C.8 D.9
8.如图,P是等边△ABC形内一点,连接PA、PB、PC,PA:PB:PC=3:4:5,以AC为边在形外作△AP′C≌△APB,连接PP′,则以下结论错误的是( )
A.△APP'是正三角形B.△PCP'是直角三角形C.∠APB=150° D.∠APC=135°
二、填空题
9.如图,为庆祝渝北中学艺术节,学校准备组建合唱团进行表演,欲在如图所示的阶梯形站台上铺设红色地毯,已知这种地毯每平方米售价为40元,站台宽为,则购买这种地毯至少需要 元.
10.如图,在 ABC中,,,,,将 ABC沿直线向右平移3个单位长度得到,连接,则下列结论:①,;②;③四边形的周长是27;④点A到直线的距离是.其中正确的是 .(填写所有正确的序号)
11.如图,在中,,,,M,E分别是边上两个动点,并满足,过点M作交于点F,点H在内,且,.点G在上运动,连接,,当的值最小时,的长为 .
12.如图,在 ABC中,,以为圆心,以的长为半径作弧交于点,再分别以,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点,若,,则 .
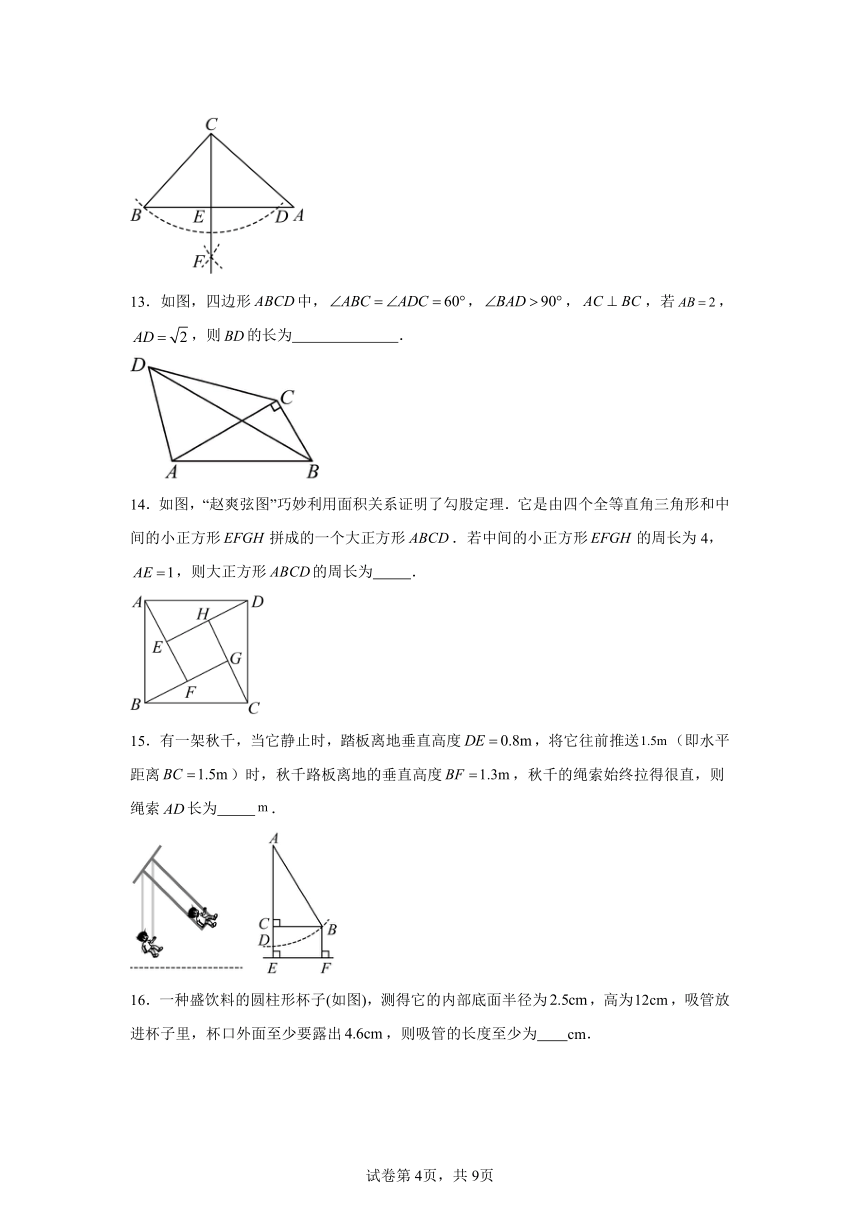
13.如图,四边形中,,,,若,,则的长为 .
14.如图,“赵爽弦图”巧妙利用面积关系证明了勾股定理.它是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.若中间的小正方形的周长为4,,则大正方形的周长为 .
15.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送(即水平距离)时,秋千路板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
16.一种盛饮料的圆柱形杯子(如图),测得它的内部底面半径为,高为,吸管放进杯子里,杯口外面至少要露出,则吸管的长度至少为 cm.
三、解答题
17.如图,在四边形中,∠B=90°,,,.
(1)求的度数;
(2)求四边形的面积.
18.如图,将长方形沿对角线翻折,点落在点处,交于.
(1)求证:是等腰三角形;
(2)若,,求图中的面积.
19.甲、乙两艘搜救艇接到消息,在海面上有遇险船只从A,B两地发出求救信号.甲搜救艇立即以15海里/时的速度离开港口O,沿北偏西50°的方向向A地出发,同时乙搜救艇也从港口O出发,以20海里/时的速度向B地出发,2小时后他们同时到达各自的目标位置,且相距50海里.
(1)求乙搜救艇的航行方向;
(2)成功救援后,甲、乙两艘搜救艇同时沿原路方向返回港口O,其速度分别是12海里/时、16海里/时,1小时后甲、乙两艘搜救艇分别在点E,F处,此时甲、乙两艘搜救艇相距多少海里?
20.周末,小斌在父母的陪伴下坐车外出游玩.在一段笔直的公路段外有一个景点C,由于视线遮挡原因.只有在离景点C250m以内的区域才能欣赏景点已知,,.
(1)请通过计算说明小斌一家在公路AB段行驶时能否欣赏到景点C?
(2)已知在公路AB段欣赏景点C的足够时间为18s,小斌家汽车在AB段以的速度匀速行驶.请你通过计算判断小斌家在公路AB段欣赏景点C的时间足够吗?
21.为了让学生更好地学会用勾股定理,某校八年级数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题,利用课余时间完成了实践调查,并利用皮尺等工具采集了如下的实验数据.
【采集数据】
如图,利用皮尺测量水平距离米,然后根据手中剩余风筝线的长度得出风筝线的长度米,最后测量放风筝的小康同学的身高米.
【数据应用】
当点均在同一平面内,已知图中各点均在同一平面内,点,,,在同一直线上.
(1)求此时风筝的垂直高度.
(2)若站在点不动,想把风筝沿着的方向从点的位置上升18米到点的位置,则还需要放出风筝线多少米?
22.在信息技术迅猛发展的今天,很多同学都能够借助网络平台进行学习,在学面直角坐标系后,小明同学在网上搜索到下面的文字材料:
如图1,在直角坐标系中任意两点,其坐标分别为和,分别过这两点作两坐标轴的平行线,构成一个直角三角形,其中直角边,利用勾股定理可得,线段的长为.
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知,则线段的长为__________;
(2)若点C在x轴上,点D的坐标是,且,求点C的坐标;
(3)如图2,在直角坐标系中,点A,B的坐标分别为和,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求周长的最小值.
23.阅读材料,并完成相应任务.
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际,所以很多人都探讨、研究它的证明,新的证法不断出现.
下面的图形是传说中毕达哥拉斯的证明图形:
证明:①在图1中,∵
4个直角三角形的面积+两个正方形的面积
=4× + + .
②在图2中,∵
4个直角三角形的面积+正方形的面积
=4× + .
∴4× + + =4× + .
整理得:
∴ .
任务:(1)将材料中的空缺部分补充完整;
(2)如图3,在△ABC中,∠A=60°,∠ACB=75°,CD⊥AB,AC=4,求BC的长.
24.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)如图1是由4个全等的直角三角形所拼成的大正方形,中间空白部分是边长为c的小正方形,请借助图1来验证勾股定理.证明:由等面积法知:
∴_____;
∴_____,得证.
(2)应用勾股定理
①应用一:在数轴上画出表示无理数的点
如图2,在数轴上找出表示2的点G,过点G作直线l垂直于数轴,在l上取点F,使,以原点O为圆心,为半径作弧,则弧与数轴的交点E表示的数是_____;
②应用二:最短路径问题
如图3,一只蚂蚁从点A沿圆柱侧面爬到相对一侧中点B处,如果圆柱的高为,圆柱的底面半径为,那么最短的路线长是_____;
③应用三:解决实际问题.
如图4,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至C处时,即水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学新人教版下册第十七章《勾股定理》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A B C C B C D
9.2800
10.①②
11.
12.//
13.
14.
15.
16.
17.(1)解:,,
,,
在 ABC中,,,
,,
,
是直角三角形,
;
(2)解:由题意得:四边形的面积 ABC的面积的面积
.
四边形的面积为.
18.(1)解:(1)∵四边形是长方形即矩形,
∴,,,
∵将长方形沿对角线翻折,点落在点处,
∴,,,
∴,,
在与中,
,
∴
∴,
∴是等腰三角形;
(2)∵,,
∴,,
∵,
∴,,
∴,
即,
∴,
∴
.
∴图中的面积为.
19.(1)解:由题意可得:海里,海里,
∵海里,
∴,,
∵,
∴,
即乙搜救艇的航行方向是北偏东方向;
(2)解:由题意,海里,海里,
∴海里,海里,
∵,
∴海里,
答:甲、乙两艘搜救艇相距30海里.
20.(1)解:由题意,,,,
根据面积法可得,C到的距离
如图.
以C为圆心,250m长为半径,交于点G、H,
小斌一家在公路段行驶时能欣赏到景点
(2)由题意,结合(1)图可得,,且关于对称,
,
故小斌家在公路段欣赏景点C的时间足够.
21.(1)解:由题意得,米,,
在中,由勾股定理得米,
∴米;
∴此时风筝的垂直高度为米;
(2)解:由题意得,米,
在中,由勾股定理得米,
∵米,
∴还需要放出风筝线14米.
22.(1)解:∵,
∴,
故答案为:6;
(2)解:设,
∵点的坐标是,且,
∴,
解得,
∴点的坐标是:或;
(3)解:作A点关于y轴的对称点为,则 ABC的周长最小值,
∴点的坐标为,
的周长最小值
23.(1)①在图1中,∵
4个直角三角形的面积+两个正方形的面积
=4×++.
②在图2中,∵
4个直角三角形的面积+正方形的面积
=4×+.
∴4×++ =4×+ .
整理得:
∴ .
故填:,,,
(2)∵CD⊥AB
∴∠ADC=∠BDC=90°
∵∠A=60°
∴∠ACD=30°
∵AC=4
∴AD=2
在Rt△ACD中
CD=
又∵∠ACB=75°
∴∠DCB=∠ACB-∠ACD=45°
∴∠B=45°
∴ BD=CD=
在Rt△BCD中
BC=
24.1)证明:由等面积法知:
∴,
∴,得证.
故答案为:,;
(2)解:①在中,
∵,
∴,
∴点E表示的数是,
故答案为:;
②连接,
∵圆柱的底面半径为,
∴,
在中,,
,
即蚂蚁爬行的最短路径长为.
故答案为:;
③∵,,
∴.
设秋千的绳索长为,根据题意可得,
利用勾股定理可得.
解得:.
答:绳索的长为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在Rt ABC中,,点在的延长线上,且,则的长是( )
A. B. C. D.
2.满足下列条件的 ABC中,不是直角三角形的是( )
A. B.,,
C. D.
3.如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
A. B. C. D.
4.如图,某自动感应门的正上方装着一个感应器A,离地距离,当人体进入感应范围内时,感应门就会自动打开,一个身高的学生刚走到离门间距的地方时,感应门自动打开,则该感应器感应长度为( )
A. B. C. D.
5.如图,,以为直角边作,使,再以为直角边作,使,,依此法继续作下去,则的长为( )
A. B. C. D.
6.如图,在中,,,,点为边的中点,点E在边上,且,则的长为( )
A.2 B. C. D.3
7.在 ABC中,,为边上的中线,,平分外角,过作交于点,则的长为( )
A.6 B.7 C.8 D.9
8.如图,P是等边△ABC形内一点,连接PA、PB、PC,PA:PB:PC=3:4:5,以AC为边在形外作△AP′C≌△APB,连接PP′,则以下结论错误的是( )
A.△APP'是正三角形B.△PCP'是直角三角形C.∠APB=150° D.∠APC=135°
二、填空题
9.如图,为庆祝渝北中学艺术节,学校准备组建合唱团进行表演,欲在如图所示的阶梯形站台上铺设红色地毯,已知这种地毯每平方米售价为40元,站台宽为,则购买这种地毯至少需要 元.
10.如图,在 ABC中,,,,,将 ABC沿直线向右平移3个单位长度得到,连接,则下列结论:①,;②;③四边形的周长是27;④点A到直线的距离是.其中正确的是 .(填写所有正确的序号)
11.如图,在中,,,,M,E分别是边上两个动点,并满足,过点M作交于点F,点H在内,且,.点G在上运动,连接,,当的值最小时,的长为 .
12.如图,在 ABC中,,以为圆心,以的长为半径作弧交于点,再分别以,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点,若,,则 .
13.如图,四边形中,,,,若,,则的长为 .
14.如图,“赵爽弦图”巧妙利用面积关系证明了勾股定理.它是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.若中间的小正方形的周长为4,,则大正方形的周长为 .
15.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送(即水平距离)时,秋千路板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
16.一种盛饮料的圆柱形杯子(如图),测得它的内部底面半径为,高为,吸管放进杯子里,杯口外面至少要露出,则吸管的长度至少为 cm.
三、解答题
17.如图,在四边形中,∠B=90°,,,.
(1)求的度数;
(2)求四边形的面积.
18.如图,将长方形沿对角线翻折,点落在点处,交于.
(1)求证:是等腰三角形;
(2)若,,求图中的面积.
19.甲、乙两艘搜救艇接到消息,在海面上有遇险船只从A,B两地发出求救信号.甲搜救艇立即以15海里/时的速度离开港口O,沿北偏西50°的方向向A地出发,同时乙搜救艇也从港口O出发,以20海里/时的速度向B地出发,2小时后他们同时到达各自的目标位置,且相距50海里.
(1)求乙搜救艇的航行方向;
(2)成功救援后,甲、乙两艘搜救艇同时沿原路方向返回港口O,其速度分别是12海里/时、16海里/时,1小时后甲、乙两艘搜救艇分别在点E,F处,此时甲、乙两艘搜救艇相距多少海里?
20.周末,小斌在父母的陪伴下坐车外出游玩.在一段笔直的公路段外有一个景点C,由于视线遮挡原因.只有在离景点C250m以内的区域才能欣赏景点已知,,.
(1)请通过计算说明小斌一家在公路AB段行驶时能否欣赏到景点C?
(2)已知在公路AB段欣赏景点C的足够时间为18s,小斌家汽车在AB段以的速度匀速行驶.请你通过计算判断小斌家在公路AB段欣赏景点C的时间足够吗?
21.为了让学生更好地学会用勾股定理,某校八年级数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题,利用课余时间完成了实践调查,并利用皮尺等工具采集了如下的实验数据.
【采集数据】
如图,利用皮尺测量水平距离米,然后根据手中剩余风筝线的长度得出风筝线的长度米,最后测量放风筝的小康同学的身高米.
【数据应用】
当点均在同一平面内,已知图中各点均在同一平面内,点,,,在同一直线上.
(1)求此时风筝的垂直高度.
(2)若站在点不动,想把风筝沿着的方向从点的位置上升18米到点的位置,则还需要放出风筝线多少米?
22.在信息技术迅猛发展的今天,很多同学都能够借助网络平台进行学习,在学面直角坐标系后,小明同学在网上搜索到下面的文字材料:
如图1,在直角坐标系中任意两点,其坐标分别为和,分别过这两点作两坐标轴的平行线,构成一个直角三角形,其中直角边,利用勾股定理可得,线段的长为.
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知,则线段的长为__________;
(2)若点C在x轴上,点D的坐标是,且,求点C的坐标;
(3)如图2,在直角坐标系中,点A,B的坐标分别为和,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求周长的最小值.
23.阅读材料,并完成相应任务.
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际,所以很多人都探讨、研究它的证明,新的证法不断出现.
下面的图形是传说中毕达哥拉斯的证明图形:
证明:①在图1中,∵
4个直角三角形的面积+两个正方形的面积
=4× + + .
②在图2中,∵
4个直角三角形的面积+正方形的面积
=4× + .
∴4× + + =4× + .
整理得:
∴ .
任务:(1)将材料中的空缺部分补充完整;
(2)如图3,在△ABC中,∠A=60°,∠ACB=75°,CD⊥AB,AC=4,求BC的长.
24.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)如图1是由4个全等的直角三角形所拼成的大正方形,中间空白部分是边长为c的小正方形,请借助图1来验证勾股定理.证明:由等面积法知:
∴_____;
∴_____,得证.
(2)应用勾股定理
①应用一:在数轴上画出表示无理数的点
如图2,在数轴上找出表示2的点G,过点G作直线l垂直于数轴,在l上取点F,使,以原点O为圆心,为半径作弧,则弧与数轴的交点E表示的数是_____;
②应用二:最短路径问题
如图3,一只蚂蚁从点A沿圆柱侧面爬到相对一侧中点B处,如果圆柱的高为,圆柱的底面半径为,那么最短的路线长是_____;
③应用三:解决实际问题.
如图4,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至C处时,即水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
试卷第1页,共3页
试卷第1页,共3页
《八年级数学新人教版下册第十七章《勾股定理》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A B C C B C D
9.2800
10.①②
11.
12.//
13.
14.
15.
16.
17.(1)解:,,
,,
在 ABC中,,,
,,
,
是直角三角形,
;
(2)解:由题意得:四边形的面积 ABC的面积的面积
.
四边形的面积为.
18.(1)解:(1)∵四边形是长方形即矩形,
∴,,,
∵将长方形沿对角线翻折,点落在点处,
∴,,,
∴,,
在与中,
,
∴
∴,
∴是等腰三角形;
(2)∵,,
∴,,
∵,
∴,,
∴,
即,
∴,
∴
.
∴图中的面积为.
19.(1)解:由题意可得:海里,海里,
∵海里,
∴,,
∵,
∴,
即乙搜救艇的航行方向是北偏东方向;
(2)解:由题意,海里,海里,
∴海里,海里,
∵,
∴海里,
答:甲、乙两艘搜救艇相距30海里.
20.(1)解:由题意,,,,
根据面积法可得,C到的距离
如图.
以C为圆心,250m长为半径,交于点G、H,
小斌一家在公路段行驶时能欣赏到景点
(2)由题意,结合(1)图可得,,且关于对称,
,
故小斌家在公路段欣赏景点C的时间足够.
21.(1)解:由题意得,米,,
在中,由勾股定理得米,
∴米;
∴此时风筝的垂直高度为米;
(2)解:由题意得,米,
在中,由勾股定理得米,
∵米,
∴还需要放出风筝线14米.
22.(1)解:∵,
∴,
故答案为:6;
(2)解:设,
∵点的坐标是,且,
∴,
解得,
∴点的坐标是:或;
(3)解:作A点关于y轴的对称点为,则 ABC的周长最小值,
∴点的坐标为,
的周长最小值
23.(1)①在图1中,∵
4个直角三角形的面积+两个正方形的面积
=4×++.
②在图2中,∵
4个直角三角形的面积+正方形的面积
=4×+.
∴4×++ =4×+ .
整理得:
∴ .
故填:,,,
(2)∵CD⊥AB
∴∠ADC=∠BDC=90°
∵∠A=60°
∴∠ACD=30°
∵AC=4
∴AD=2
在Rt△ACD中
CD=
又∵∠ACB=75°
∴∠DCB=∠ACB-∠ACD=45°
∴∠B=45°
∴ BD=CD=
在Rt△BCD中
BC=
24.1)证明:由等面积法知:
∴,
∴,得证.
故答案为:,;
(2)解:①在中,
∵,
∴,
∴点E表示的数是,
故答案为:;
②连接,
∵圆柱的底面半径为,
∴,
在中,,
,
即蚂蚁爬行的最短路径长为.
故答案为:;
③∵,,
∴.
设秋千的绳索长为,根据题意可得,
利用勾股定理可得.
解得:.
答:绳索的长为.
答案第1页,共2页
答案第1页,共2页
