4.1.2变量与函数 教案

中小学教育资源及组卷应用平台
分课时教学设计
第2课时《4.1.2变量与函数 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 让学生通过实际操作，体会函数的三种表示方法在实际生活中的应用价值，以激发学生对数学的学习兴趣.
学习者分析 使学生在探索、归纳求函数自变量取值范围的过程中，增强数学建模意识；联系求代数式的值的知识，探索求函数值的方法.
教学目标 1.会根据实际问题构建数学模型并列出函数解析式； 2.掌握函数的三种表示方法，根据函数值求对应自变量的值．
教学重点 求函数解析式．
教学难点 会在简单的情况下根据实际背景对自变量的限制求出自变量的取值范围.
学习活动设计
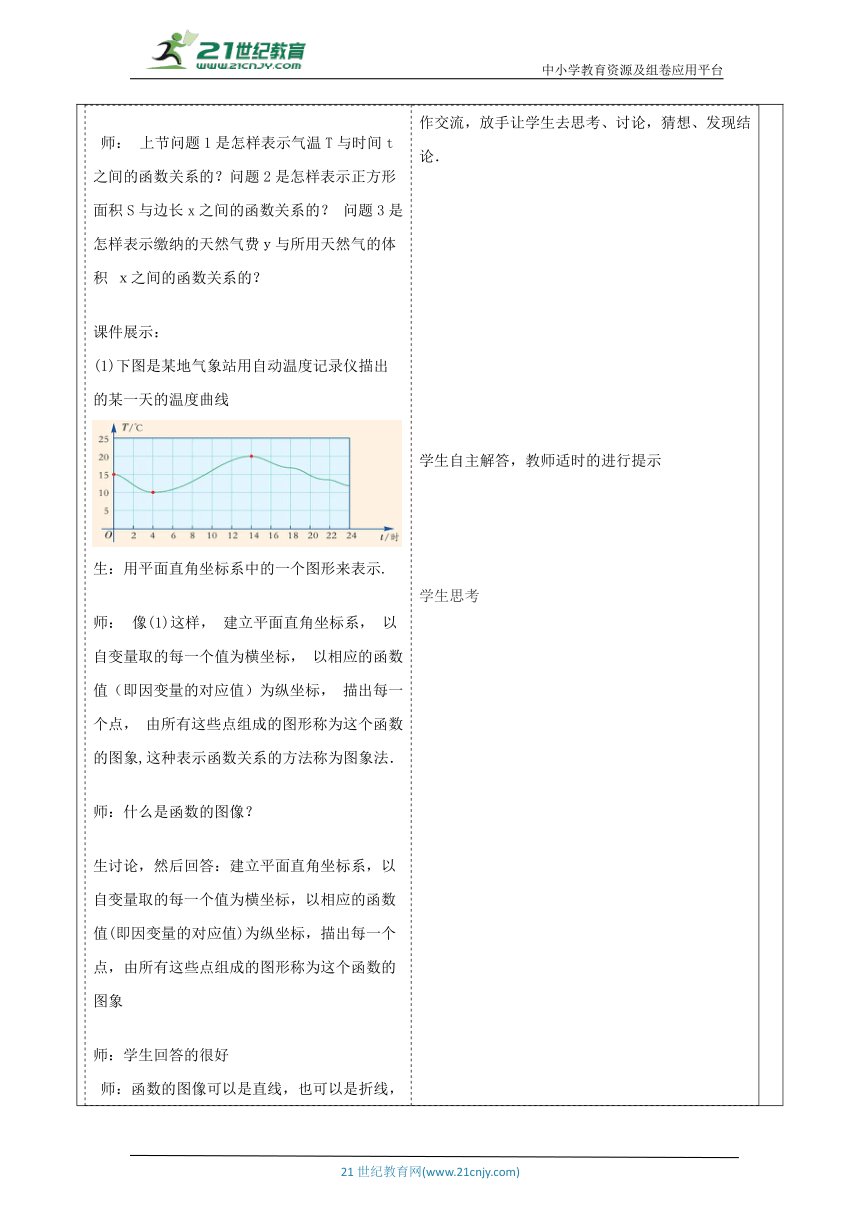
教师活动学生活动环节一：引入新课 师：上节课我们学习了函数的概念，你能说出什么叫做函数吗？ 生：一般地，如果变量y随着变量x而变化，并且对于x取的每一个值，y都有唯一的一个值与它对应，那么称y是x的函数．学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索.会根据实际问题构建数学模型并列出函数解析式． 环节二：新知探究教师活动2： 师： 上节问题1是怎样表示气温T与时间t之间的函数关系的？问题2是怎样表示正方形面积S与边长x之间的函数关系的？ 问题3是怎样表示缴纳的天然气费ｙ与所用天然气的体积 ｘ之间的函数关系的？ 课件展示： (1)下图是某地气象站用自动温度记录仪描出的某一天的温度曲线 生：用平面直角坐标系中的一个图形来表示. 师： 像(1)这样， 建立平面直角坐标系， 以自变量取的每一个值为横坐标， 以相应的函数值（即因变量的对应值）为纵坐标， 描出每一个点， 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法． 师：什么是函数的图像？ 生讨论，然后回答：建立平面直角坐标系，以自变量取的每一个值为横坐标，以相应的函数值(即因变量的对应值)为纵坐标，描出每一个点，由所有这些点组成的图形称为这个函数的图象 师：学生回答的很好 师：函数的图像可以是直线，也可以是折线，也可以是曲线 函数的图像是函数关系式的具体反映，因此在画函数图像时，一定要注意自变量的取值范围 师：再看第(2)个问题，课件展示： （2）正方形的面积S与边长x的取值如下表，S是不是x的函数？ 生：列一张表来表示. 师：这是函数的什么表示方法呢？ 生：像（2）这样，列一张表，第一行表示自变量取的各个值，第二行表示相应的函数值（即因变量的对应值），这种表示函数关系的方法称为列表法． 师：问题3，课件展示： (3)某城市居民用的天然气，１m3收费2.88元，使用x (m3） 天然气应缴纳的费用y(元)为y = 2.88x． y是不是x 的函数？ 生：我们可以用一个式子y=2.88x来表示 师：那么我们来总结一下这种表示方法吧 生：像（3）这样，用式子表示函数关系的方法称为公式法，这样的式子称为函数的表达式． 师：
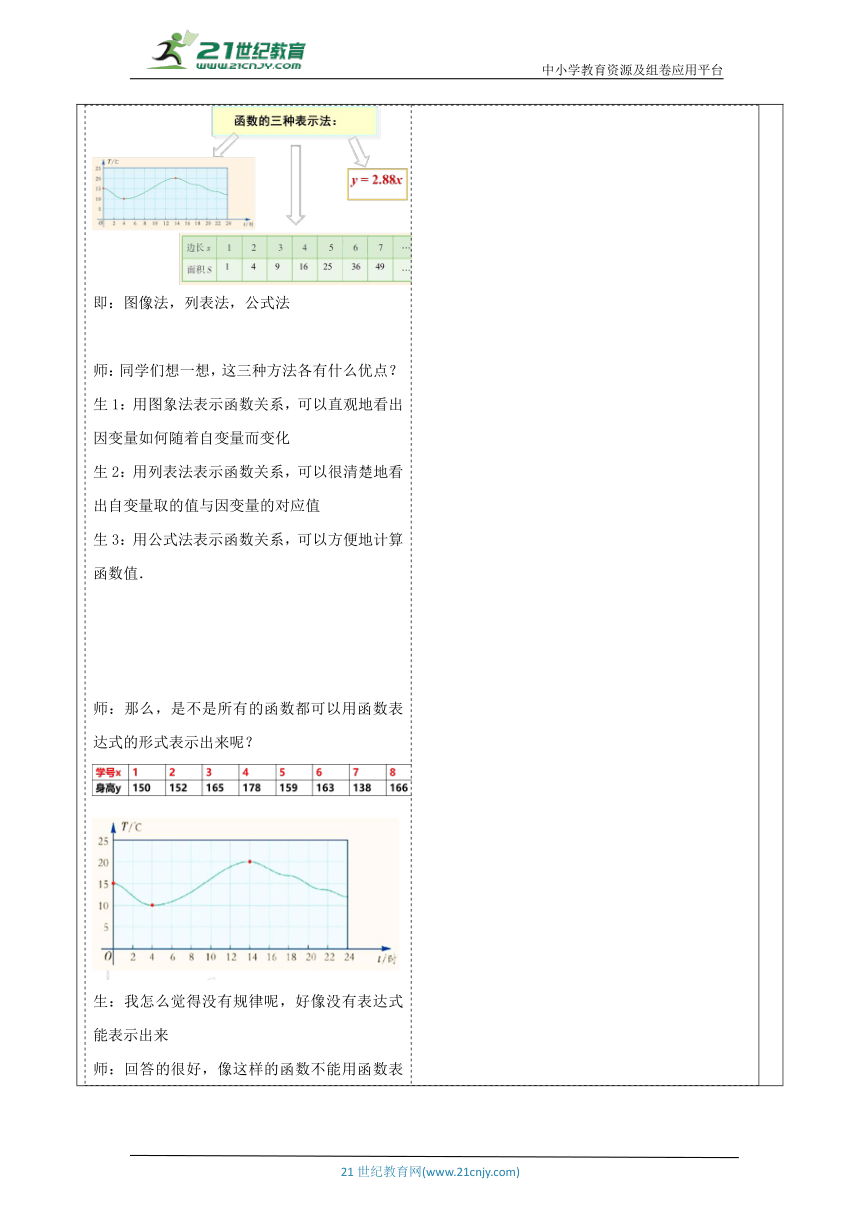
我们能总结出函数的表达方法吗？ 生：函数的三种表示法： 即：图像法，列表法，公式法 师：同学们想一想，这三种方法各有什么优点？ 生1：用图象法表示函数关系，可以直观地看出因变量如何随着自变量而变化 生2：用列表法表示函数关系，可以很清楚地看出自变量取的值与因变量的对应值 生3：用公式法表示函数关系，可以方便地计算函数值． 师：那么，是不是所有的函数都可以用函数表达式的形式表示出来呢？ 生：我怎么觉得没有规律呢，好像没有表达式能表示出来 师：回答的很好，像这样的函数不能用函数表达式的形式表示 师：我们来看一下这个问题，课件展示 用边长为1的等边三角形拼成如图所示的图形，用y 表示拼成的图形的周长，用n表示其中等边三角形的数目，显然拼成的图形的周长y是n的函数． （1）填写下表： 生：这是列表法 师：掌握的很好 （2）试用公式法表示这个函数关系. 周长y与三角形个数n之间的函数表达式是y=n+2 师：想一想，函数y=n+2中n可以取任意实数吗？ 生：因为n是图形的序号，所以只能为正整数. 故，此函数应表示为：y=n+2(n为正整数) 师：所以我们在写函数公式法时注意自变量的范围 注意：用解析式表示函数时，一般要加上自变量的取值范围 师生共同总结：一般地，对自变量的取值范围的确定，主要从两个方面去考虑 1、自变量的取值要使函数解析式有意义； 2、自变量的取值要使实际问题有意义； （3）试用图象法表示这个函数关系. 生：因为函数y=n+2中，自变量n的取值范围是正整数集，因此在平面直角坐标系中可以描出无数个点，这些点组成了y=n+2的函数图象，如图. 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．掌握函数的三种表示方法，根据函数值求对应自变量的值。 环节三：典例精析 例1、某天7时，小明从家骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校. 图反映了他骑车的整个过程，结合图象，回答下列问题： （1）自行车发生故障是在什么时间？此时离家有多远？ （2）修车花了多长时间？修好车后又花了多长时间到达学校？ （3）小明从家到学校的平均速度是多少？ 解:(1)从横坐标看出,自行车发生故障的时间是7：05；从纵坐标看出，此时离家1000 m. (2)从横坐标看出，小明修车花了15 min；小明修好车后又花了10min到达学校. (3)从纵坐标看出，小明家离学校2100 m；从横坐标看出，他在路上共花了30min，因此，他从家到学校的平均速度是 2100÷30=70（m/min）. 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，会在简单的情况下根据实际背景对自变量的限制求出自变量的取值范围．
板书设计
课堂练习 【知识技能类作业】 必做题： 1.升旗时，旗子的高度h(米)与时间t(分)的函数图象大致为( ) 选做题： 2.一辆汽车以60 km/h的速度在潭邵公路上行驶，它行驶的路程s(km)与时间t(h)的关系用公式表示为:__________. 【综合拓展类作业】 3．下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又原路返回，顺路到文具店去买笔，然后散步回家.其中x表示时间，y表示张强离家的距离.根据图象回答： (1)体育场离张强家__________千米，张强从家到体育场用了__________分钟； (2)体育场离文具店__________千米； (3)张强在文具店逗留了__________分钟； (4)请计算：张强从文具店回家的平均速度是多少？
课堂总结
作业设计 【知识技能类作业】 必做题： 1.如图，把一个小球垂直向上抛出，则下列描述该小球的运动速度v(单位：m/s)与运动时间t(单位：s)关系的函数图像中，正确的是( ) 选做题： 2.观察下表：则y与x的函数表达式为_________________. 【综合拓展类作业】 3. 李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天，李老师下班后，以45米/分的速度从学校往家走，走到离学校900米时，正好遇到一个朋友，停下来聊了半小时，之后以110米/分的速度走回了家.李老师回家过程中，离家的路程S（米）与所用时间t（分）之间的关系如图所示. （1）求a、b、c的值； （2）求李老师从学校到家的总时间.
教学反思
21世纪教育网(www.21cnjy.com)