4.1.2变量与函数 课件(共31张PPT)
文档属性
| 名称 | 4.1.2变量与函数 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第一章 直角三角形
4.1.2变量与函数
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.会根据实际问题构建数学模型并列出函数解析式;
2.掌握函数的三种表示方法,根据函数值求对应自变量的值
02
新知导入
什么叫做函数?
一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数.
03
新知探究
观察下列3题,它们都是怎么表示函数的?
问题1. 如图是某地气象站用自动温度记录仪描出的某一天的温度曲线.
问题2. 当正方形的边长 x 分别取1,2,3,4,5,...时,正方形的面积S分别是多少?试填写下表.
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知探究
问题3. 某城市居民用天然气收费标准为: 1(m3)收费2.88元,使用x(m3)天然气应缴纳的费用y(元)为 y = 2.88 x. 当x = 10时,缴纳的费用为多少?
说一说
(1)问题1是怎样表示气温T与时间t之间的函数关系的?
(2)问题2是怎样表示正方形面积S与边长x之间的函数关系的?
(3)问题3是怎样表示缴纳的天然气费y与所用天然气的体积 x之间的函数关系的?
03
新知讲解
(1)下图是某地气象站用自动温度记录仪描出的某一天的温度曲线
用平面直角坐标系中的一个图形来表示.
像(1)这样, 建立平面直角坐标系, 以自变量取的每一个值为横坐标, 以相应的函数值(即因变量的对应值)为纵坐标, 描出每一个点, 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法.
03
新知讲解
什么是函数的图像?
建立平面直角坐标系,以自变量取的每一个值为横坐标,以相应的函数值(即因变量的对应值)为纵坐标,描出每一个点,由所有这些点组成的图形称为这个函数的图象
函数的图像可以是直线,也可以是折线,也可以是曲线
函数的图像是函数关系式的具体反映,因此在画函数图像时,一定要注意自变量的取值范围
03
新知讲解
(2)正方形的面积S与边长x的取值如下表,S是不是x的函数?
列一张表来表示.
像(2)这样,列一张表,第一行表示自变量取的各个值,第二行表示相应的函数值(即因变量的对应值),这种表示函数关系的方法称为列表法.
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知讲解
(3)某城市居民用的天然气,1m3收费2.88元,使用x (m3) 天然气应缴纳的费用y(元)为y = 2.88x.y是不是x 的函数?
用一个式子y=2.88x来表示.
像(3)这样,用式子表示函数关系的方法称为公式法,这样的式子称为函数的表达式.
03
新知讲解
y = 2.88x
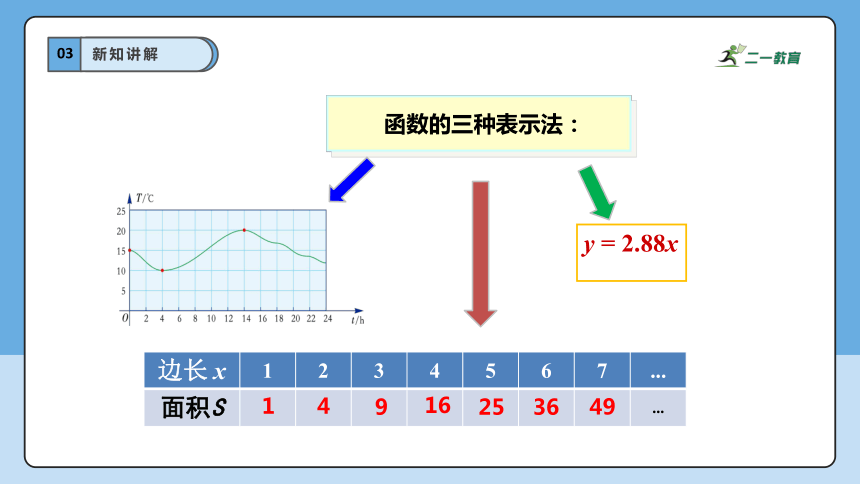
函数的三种表示法:
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知讲解
问题
用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化;
用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值;
用公式法表示函数关系,可以方便地计算函数值.
你能谈谈用图象法、列表法、公式法表示函数关系时各自的优点吗?
03
新知讲解
是不是所有的函数都可以用函数表达式的形式表示出来呢?
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
这样的函数不能用函数表达式的形式表示
03
新知讲解
动脑筋
用边长为1的等边三角形拼成如图所示的图形,用y 表示拼成的图形的周长,用n表示其中等边三角形的数目,显然拼成的图形的周长y是n的函数.
03
新知讲解
(1)填写下表:
n 1 2 3 4 5 6 7 8 …
y …
3
4
5
6
7
8
9
10
列表法
03
新知讲解
(2)试用公式法表示这个函数关系.
周长y与三角形个数n之间的函数表达式是y=n+2
公式法
思考:函数y=n+2中n可以取任意实数吗?
因为n是图形的序号,所以只能为正整数.
故,此函数应表示为:y=n+2(n为正整数)
注意:用解析式表示函数时,一般要加上自变量的取值范围
03
新知讲解
一般地,对自变量的取值范围的确定,主要从两个方面去考虑:
1、自变量的取值要使函数解析式有意义;
2、自变量的取值要使实际问题有意义;
03
新知讲解
(3)试用图象法表示这个函数关系.
因为函数y=n+2中,自变量n的取值范围是正整数集,因此在平面直角坐标系中可以描出无数个点,这些点组成了y=n+2的函数图象,如图.
通过图象可以数形结合地研究变量与变量之间的联系与变化.
图象法
新课探究
例
例1、某天7时,小明从家骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 图反映了他骑车的整个过程,结合图象,回答下列问题:
(1)自行车发生故障是在什么时间?此时离家有多远?
(2)修车花了多长时间?修好车后又花了多长时间到达学校?
(3)小明从家到学校的平均速度是多少?
03
新知讲解
解:(1)从横坐标看出,自行车发生故障的时间是7:05;从纵坐标看出,此时离家1000 m.
(2)从横坐标看出,小明修车花了15 min;小明修好车后又花了10min到达学校.
(3)从纵坐标看出,小明家离学校2100 m;从横坐标看出,他在路上共花了30min,因此,他从家到学校的平均速度是 2100÷30=70(m/min).
04
课堂练习
【知识技能类作业】必做题:
升旗时,旗子的高度h(米)与时间t(分)的函数图象大致为( )
B
04
课堂练习
【知识技能类作业】选做题:
3.一辆汽车以60 km/h的速度在潭邵公路上行驶,它行驶的路程s(km)与时间t(h)的关系用公式表示为:__________.
s=60t
04
课堂练习
【综合拓展类作业】
3.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家__________千米,张强从家到体育场用了__________分钟;
(2)体育场离文具店__________千米;
(3)张强在文具店逗留了__________分钟;
(4)请计算:张强从文具店回家的平均速度是多少?
2.5
15
1
20
04
课堂练习
【综合拓展类作业】
(4)从图象可知:文具店离张强家1.5千米,张强从文具店散步走回家花了100-65=35(分),
所以张强从文具店回家的平均速度是 (千米/分).
05
课堂小结
函数的表示方法
2. 列表法
1. 图象法
3. 公式法
可以直观地看出因变量如何随着自变量而变化;
可以很清楚地看出自变量取的值与因变量的对应值;
可以方便地计算函数值.
06
作业布置
【知识技能类作业】必做题:
1.如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位:s)关系的函数图像中,正确的是( )
C
06
作业布置
【知识技能类作业】选做题:
4.观察下表:则y与x的函数表达式为_________________.
y=x3+1
06
作业布置
【综合拓展类作业】
14. 李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.【来源:21·世纪·教育·网】
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
06
作业布置
【综合拓展类作业】
3. 由图象可得出:
(1)李老师停留地点离他家的路程为:2000-900=1100(米),
900÷45=20(分).
a=20,b=1100,c=20+30=50;
(2)20+30+1100/110=60(分)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
4.1.2变量与函数
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.会根据实际问题构建数学模型并列出函数解析式;
2.掌握函数的三种表示方法,根据函数值求对应自变量的值
02
新知导入
什么叫做函数?
一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数.
03
新知探究
观察下列3题,它们都是怎么表示函数的?
问题1. 如图是某地气象站用自动温度记录仪描出的某一天的温度曲线.
问题2. 当正方形的边长 x 分别取1,2,3,4,5,...时,正方形的面积S分别是多少?试填写下表.
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知探究
问题3. 某城市居民用天然气收费标准为: 1(m3)收费2.88元,使用x(m3)天然气应缴纳的费用y(元)为 y = 2.88 x. 当x = 10时,缴纳的费用为多少?
说一说
(1)问题1是怎样表示气温T与时间t之间的函数关系的?
(2)问题2是怎样表示正方形面积S与边长x之间的函数关系的?
(3)问题3是怎样表示缴纳的天然气费y与所用天然气的体积 x之间的函数关系的?
03
新知讲解
(1)下图是某地气象站用自动温度记录仪描出的某一天的温度曲线
用平面直角坐标系中的一个图形来表示.
像(1)这样, 建立平面直角坐标系, 以自变量取的每一个值为横坐标, 以相应的函数值(即因变量的对应值)为纵坐标, 描出每一个点, 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法.
03
新知讲解
什么是函数的图像?
建立平面直角坐标系,以自变量取的每一个值为横坐标,以相应的函数值(即因变量的对应值)为纵坐标,描出每一个点,由所有这些点组成的图形称为这个函数的图象
函数的图像可以是直线,也可以是折线,也可以是曲线
函数的图像是函数关系式的具体反映,因此在画函数图像时,一定要注意自变量的取值范围
03
新知讲解
(2)正方形的面积S与边长x的取值如下表,S是不是x的函数?
列一张表来表示.
像(2)这样,列一张表,第一行表示自变量取的各个值,第二行表示相应的函数值(即因变量的对应值),这种表示函数关系的方法称为列表法.
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知讲解
(3)某城市居民用的天然气,1m3收费2.88元,使用x (m3) 天然气应缴纳的费用y(元)为y = 2.88x.y是不是x 的函数?
用一个式子y=2.88x来表示.
像(3)这样,用式子表示函数关系的方法称为公式法,这样的式子称为函数的表达式.
03
新知讲解
y = 2.88x
函数的三种表示法:
边长 x 1 2 3 4 5 6 7 ...
面积S ...
1
4
9
16
25
36
49
03
新知讲解
问题
用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化;
用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值;
用公式法表示函数关系,可以方便地计算函数值.
你能谈谈用图象法、列表法、公式法表示函数关系时各自的优点吗?
03
新知讲解
是不是所有的函数都可以用函数表达式的形式表示出来呢?
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
这样的函数不能用函数表达式的形式表示
03
新知讲解
动脑筋
用边长为1的等边三角形拼成如图所示的图形,用y 表示拼成的图形的周长,用n表示其中等边三角形的数目,显然拼成的图形的周长y是n的函数.
03
新知讲解
(1)填写下表:
n 1 2 3 4 5 6 7 8 …
y …
3
4
5
6
7
8
9
10
列表法
03
新知讲解
(2)试用公式法表示这个函数关系.
周长y与三角形个数n之间的函数表达式是y=n+2
公式法
思考:函数y=n+2中n可以取任意实数吗?
因为n是图形的序号,所以只能为正整数.
故,此函数应表示为:y=n+2(n为正整数)
注意:用解析式表示函数时,一般要加上自变量的取值范围
03
新知讲解
一般地,对自变量的取值范围的确定,主要从两个方面去考虑:
1、自变量的取值要使函数解析式有意义;
2、自变量的取值要使实际问题有意义;
03
新知讲解
(3)试用图象法表示这个函数关系.
因为函数y=n+2中,自变量n的取值范围是正整数集,因此在平面直角坐标系中可以描出无数个点,这些点组成了y=n+2的函数图象,如图.
通过图象可以数形结合地研究变量与变量之间的联系与变化.
图象法
新课探究
例
例1、某天7时,小明从家骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 图反映了他骑车的整个过程,结合图象,回答下列问题:
(1)自行车发生故障是在什么时间?此时离家有多远?
(2)修车花了多长时间?修好车后又花了多长时间到达学校?
(3)小明从家到学校的平均速度是多少?
03
新知讲解
解:(1)从横坐标看出,自行车发生故障的时间是7:05;从纵坐标看出,此时离家1000 m.
(2)从横坐标看出,小明修车花了15 min;小明修好车后又花了10min到达学校.
(3)从纵坐标看出,小明家离学校2100 m;从横坐标看出,他在路上共花了30min,因此,他从家到学校的平均速度是 2100÷30=70(m/min).
04
课堂练习
【知识技能类作业】必做题:
升旗时,旗子的高度h(米)与时间t(分)的函数图象大致为( )
B
04
课堂练习
【知识技能类作业】选做题:
3.一辆汽车以60 km/h的速度在潭邵公路上行驶,它行驶的路程s(km)与时间t(h)的关系用公式表示为:__________.
s=60t
04
课堂练习
【综合拓展类作业】
3.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家__________千米,张强从家到体育场用了__________分钟;
(2)体育场离文具店__________千米;
(3)张强在文具店逗留了__________分钟;
(4)请计算:张强从文具店回家的平均速度是多少?
2.5
15
1
20
04
课堂练习
【综合拓展类作业】
(4)从图象可知:文具店离张强家1.5千米,张强从文具店散步走回家花了100-65=35(分),
所以张强从文具店回家的平均速度是 (千米/分).
05
课堂小结
函数的表示方法
2. 列表法
1. 图象法
3. 公式法
可以直观地看出因变量如何随着自变量而变化;
可以很清楚地看出自变量取的值与因变量的对应值;
可以方便地计算函数值.
06
作业布置
【知识技能类作业】必做题:
1.如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位:s)关系的函数图像中,正确的是( )
C
06
作业布置
【知识技能类作业】选做题:
4.观察下表:则y与x的函数表达式为_________________.
y=x3+1
06
作业布置
【综合拓展类作业】
14. 李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.【来源:21·世纪·教育·网】
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
06
作业布置
【综合拓展类作业】
3. 由图象可得出:
(1)李老师停留地点离他家的路程为:2000-900=1100(米),
900÷45=20(分).
a=20,b=1100,c=20+30=50;
(2)20+30+1100/110=60(分)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
