高中数学人教A版选修2-3 第一章:1.1.1 两个计数原理(一)(共11张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-3 第一章:1.1.1 两个计数原理(一)(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 630.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-29 00:00:00 | ||
图片预览




文档简介
课件11张PPT。1.1.1 两个计数原理(一)人教A版选修2-3 第一章问题1:. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以,从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
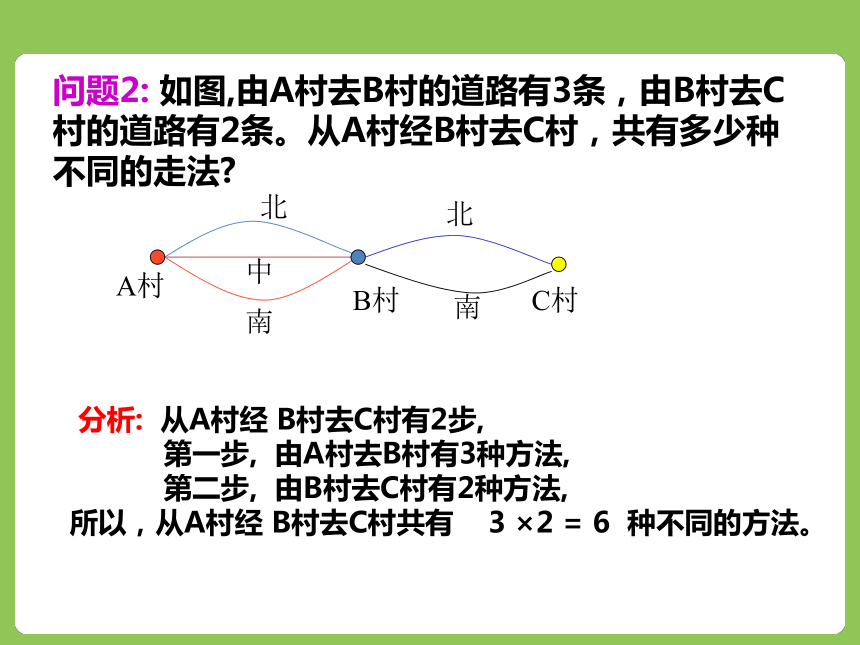
(一)新课引入:问题2: 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以,从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。
分类计数原理: 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
例 1. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
分析: (1)从书架上任取1本书,有三类办法:第一类办法, 从第1层中任取一本书, 共有 m1 = 4 种不同的方法; 第二类办法, 从第2层中任取一本书, 共有 m2 = 3 种不同的方法;第三类办法:从第3层中任取一本书,共有 m3 = 2 种不同的方法
所以, 根据分类记数原理, 得到不同选法种数共有
N = 4+3+2= 9 种。
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类记数原理”;“分步完成”用“分步记数原理”。
(三)例题讲解例 1. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类计数原理”;“分步完成”用“分步计数原理”。
(三)例题讲解分析:(2)从书架的第1,2,3层各取1本书,可以分成三个步骤例2(课后练习2改编题)
现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名,问:
(1)从中任选1人参加接待外宾的活动,有多少种不同的选 法?
(2)从3个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法?
(3)从3个年级中推行选2人,2人来自不同的年级,有多少中不同的选法?既有分类又有分步,先分类再分步两种计数原理的综合应用例3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?分析:三种方法:
(1)按个位数来分;
(2)按十位数来分;
(3)按个位数和十位数的大小关系来分例5 .从1,2,3,4,7,9这6个数中任取两个不相同的数,分别作为对数的底数与真数,能得到多少个不同的对数值?变式:用1,2,3,4,7,9编成5位数的电话号码,共有多少种编法?变式:用1,2,3,4,7,9组成5位数(各个数位均不相同),能组成多少个数?变式:用0,1,2,3,4,7,9组成5位数(各个数位均不相同),能组成多少个数?联系:分类加法计数原理和分步乘法计数原理,回答的都是关于完成一件事情的不同方法的种数问题;区别:
分类要做到“不重不漏”,各种方法是相互独立的,用任何一种方法都能完成这件事;
分步要做到“步骤完整”,各个步骤都完成才能完成这修的事情.小结:
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以,从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
(一)新课引入:问题2: 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以,从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。
分类计数原理: 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
例 1. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
分析: (1)从书架上任取1本书,有三类办法:第一类办法, 从第1层中任取一本书, 共有 m1 = 4 种不同的方法; 第二类办法, 从第2层中任取一本书, 共有 m2 = 3 种不同的方法;第三类办法:从第3层中任取一本书,共有 m3 = 2 种不同的方法
所以, 根据分类记数原理, 得到不同选法种数共有
N = 4+3+2= 9 种。
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类记数原理”;“分步完成”用“分步记数原理”。
(三)例题讲解例 1. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类计数原理”;“分步完成”用“分步计数原理”。
(三)例题讲解分析:(2)从书架的第1,2,3层各取1本书,可以分成三个步骤例2(课后练习2改编题)
现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名,问:
(1)从中任选1人参加接待外宾的活动,有多少种不同的选 法?
(2)从3个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法?
(3)从3个年级中推行选2人,2人来自不同的年级,有多少中不同的选法?既有分类又有分步,先分类再分步两种计数原理的综合应用例3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?分析:三种方法:
(1)按个位数来分;
(2)按十位数来分;
(3)按个位数和十位数的大小关系来分例5 .从1,2,3,4,7,9这6个数中任取两个不相同的数,分别作为对数的底数与真数,能得到多少个不同的对数值?变式:用1,2,3,4,7,9编成5位数的电话号码,共有多少种编法?变式:用1,2,3,4,7,9组成5位数(各个数位均不相同),能组成多少个数?变式:用0,1,2,3,4,7,9组成5位数(各个数位均不相同),能组成多少个数?联系:分类加法计数原理和分步乘法计数原理,回答的都是关于完成一件事情的不同方法的种数问题;区别:
分类要做到“不重不漏”,各种方法是相互独立的,用任何一种方法都能完成这件事;
分步要做到“步骤完整”,各个步骤都完成才能完成这修的事情.小结:
