安徽省芜湖市无为市2024-2025学年八年级下册数学期中试卷(图片版,含答案)
文档属性
| 名称 | 安徽省芜湖市无为市2024-2025学年八年级下册数学期中试卷(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 20:22:03 | ||
图片预览

文档简介
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
2024-2025学年第二学期八年级期中学情调研
数学参考答案及评分标准
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D A B C C B A
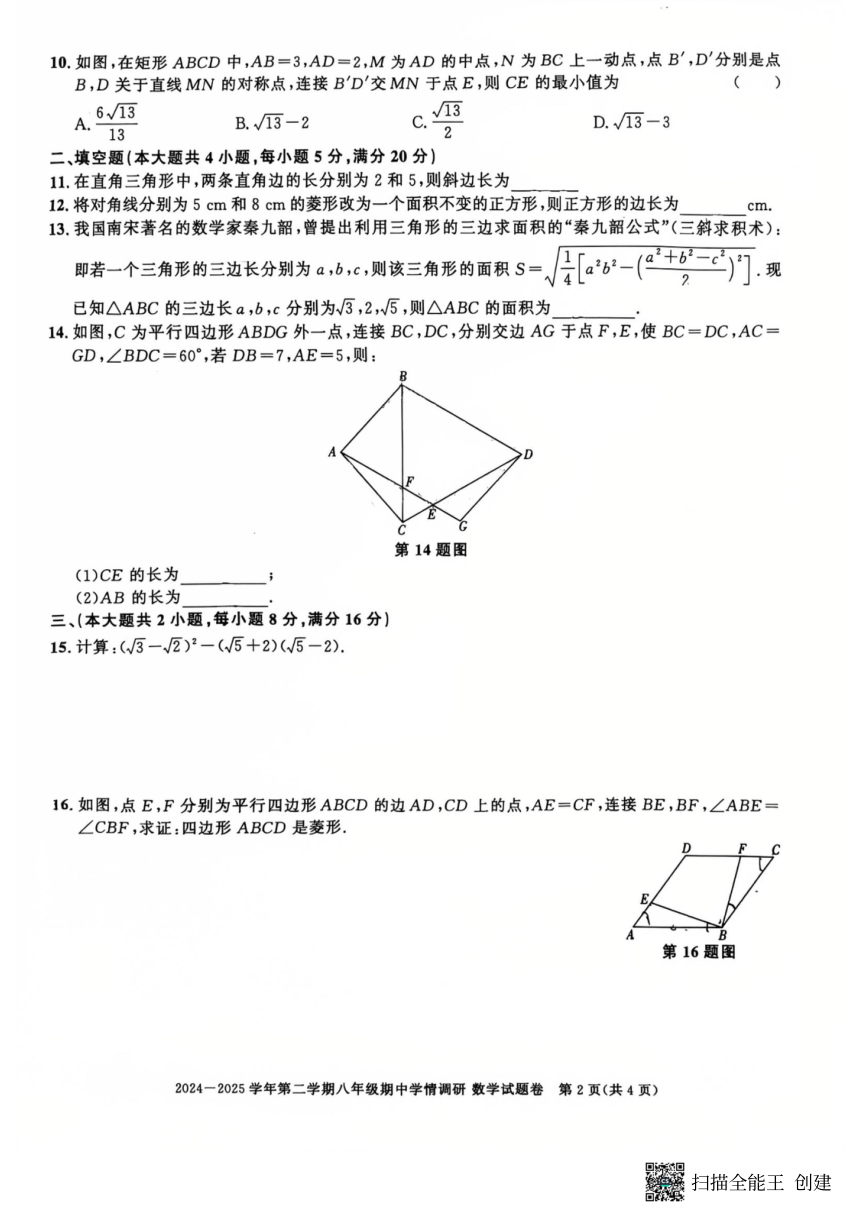
10.A
解析:如图,连接 BD,由对称性得∠DEM =∠D'EM =∠B'EN = A M D
∠BEN,∴点B,E,D 共线,即点E 在BD 上,∴当CE⊥BD 时, D′
CE 最小,∵四边形 ABCD 是矩形,∴∠BAD=90°,∴BD= E
2 1 1AB +AD2= 32+22= 13,又∵S△BCD=2BC×CD=2BD× B′
B C
, BC×CD 3×2 6 13 6 13
N
CE ∴CE= BD = =
,∴CE 的最小值为13 13 .13
故选A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11
11.29 12.25 13.2
14.(1)2;(2分)(2)19.(3分)
解析:(1)∵四边形ABDG 是平行四边形,∴AB=DG,BD=AG=7,∴AC=GD=
AB,EG=AG-AE=7-5=2,∵BC=DC,∠BDC=60°,∴△BCD 为等边三角
形,∴BC=DC=BD=7,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ABD=
60°+∠ABC,∵∠ACE=60°+∠ACB,∴∠AGD=∠ACE,在△DGE 和△ACE
∠DEG=∠AEC
中, ∠DGE=∠ACE,∴△DGE≌△ACE(AAS),∴EG=CE=2;
DG=AC
(2)如图,过点C 作CM⊥EF 于点M,∵AG//BD,∴∠CEF=∠CDB=60°,
∴∠ECM=30°,∵CE=2,∴EM=1,CM= 3,∴AM=AE-EM=5-1=4,
∴AC= AM2+CM2= 16+3= 19,∴AB=AC= 19.
B
A D
F M
E
C G
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 1页(共4页)
三、(本大题共2小题,每小题8分,满分16分)
15.解:原式=3-26+2-(5-4)
=5-26-1
=4-26. ……(8分)
16.证明:∵四边形ABCD 是平行四边形,∴∠A=∠C,
∠ABE=∠CBF
在△ABE 和△CBF 中, ∠A=∠C ,
AE=CF
∴△ABE≌△CBF(AAS),∴AB=CB,
∵四边形ABCD 是平行四边形,且AB=CB,
∴四边形ABCD 是菱形. ……(8分)
四、(本大题共2小题,每小题8分,满分16分)
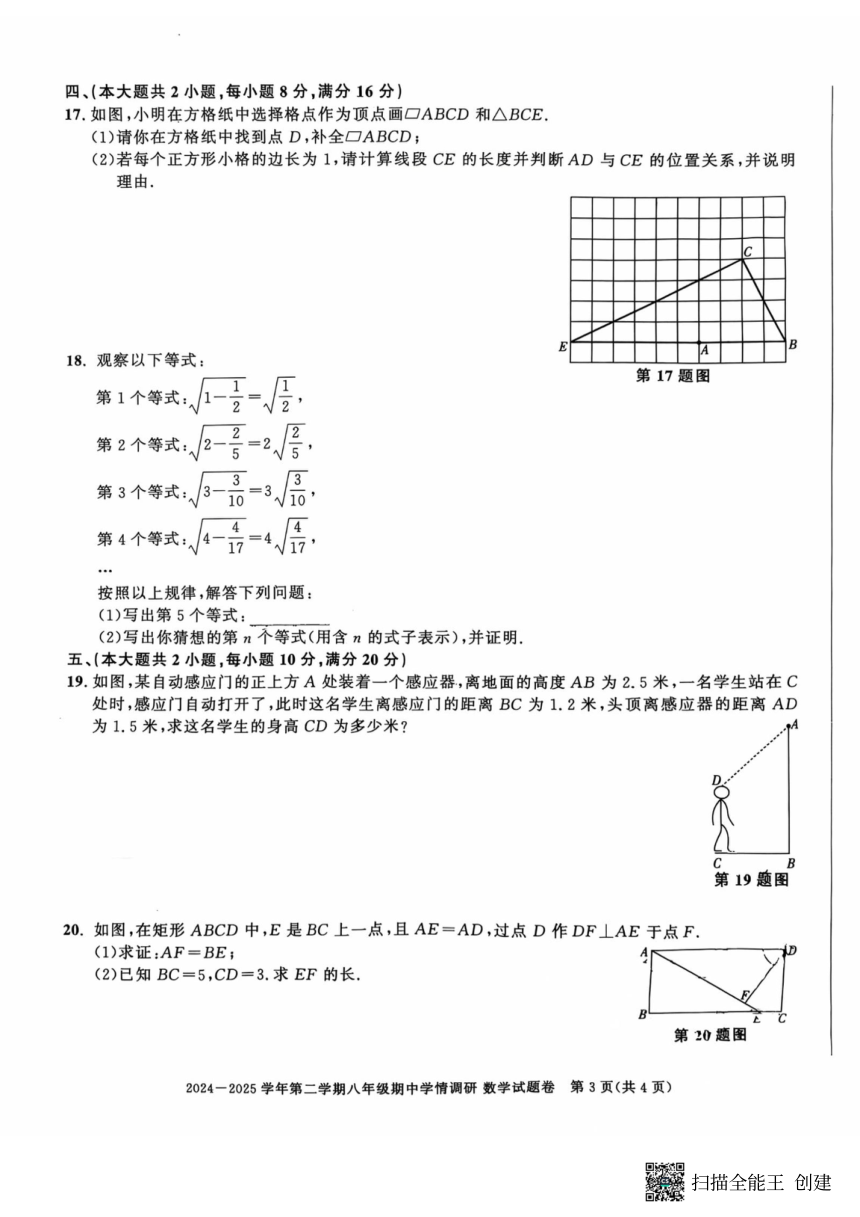
17.解:(1)如图, ABCD 即为所求; ……(3分)
D C
E A B
(2)由图可得BC= 22+42=25,CE= 42+82=45,BE=10,
∴BC2+CE2=BE2,
∴△BCE 是直角三角形,∴BC⊥CE,
∵四边形ABCD 是平行四边形,∴AD//BC,∴AD⊥CE. ……(8分)
18.解:(
5 5
1)5- =5 ; ……(2分)26 26
( n n2)猜想第n 个等式为 n- 2 =n 2 . ……(5分)n +1 n +1
3 3
证明:等式左边 n +n n n n=
n2
-
+1 n2
= 2 =n 2 =等式右边,+1 n +1 n +1
故等式成立. ……(8分)
五、(本大题共2小题,每小题10分,满分20分)
19.解:如图,过点D 作DE⊥AB 于E,
则CD=BE,DE=BC=1.2米,
在Rt△ADE 中,AD=1.5米,
由勾股定理得AE= AD2-DE2= 1.52-1.22=0.9(米),
∴BE=AB-AE=2.5-0.9=1.6(米),
∴CD=BE=1.6米,
答:这名学生的身高CD 为1.6米. ……(10分)
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 2页(共4页)
A
D E
C B
20.解:(1)证明:∵四边形ABCD 是矩形,∴AD∥BC,∠ABE=90°,∴∠DAF=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠ABE=∠DFA.
∠AFD=∠EBA
在△ADF 和△EAB 中, ∠DAF=∠AEB,
AD=AE
∴△ADF≌△EAB(AAS),∴AF=BE; ……(5分)
(2)∵四边形ABCD 是矩形,BC=5,CD=3,
∴AD=BC=5,AB=CD=3,∠B=90°,
∵AD=AE,∴AE=5,∴BE= AE2-AB2= 52-32=4,
由(1)知AF=BE,∴AF=4,
∴EF=AE-AF=5-4=1. ……(10分)
六、(本题满分12分)
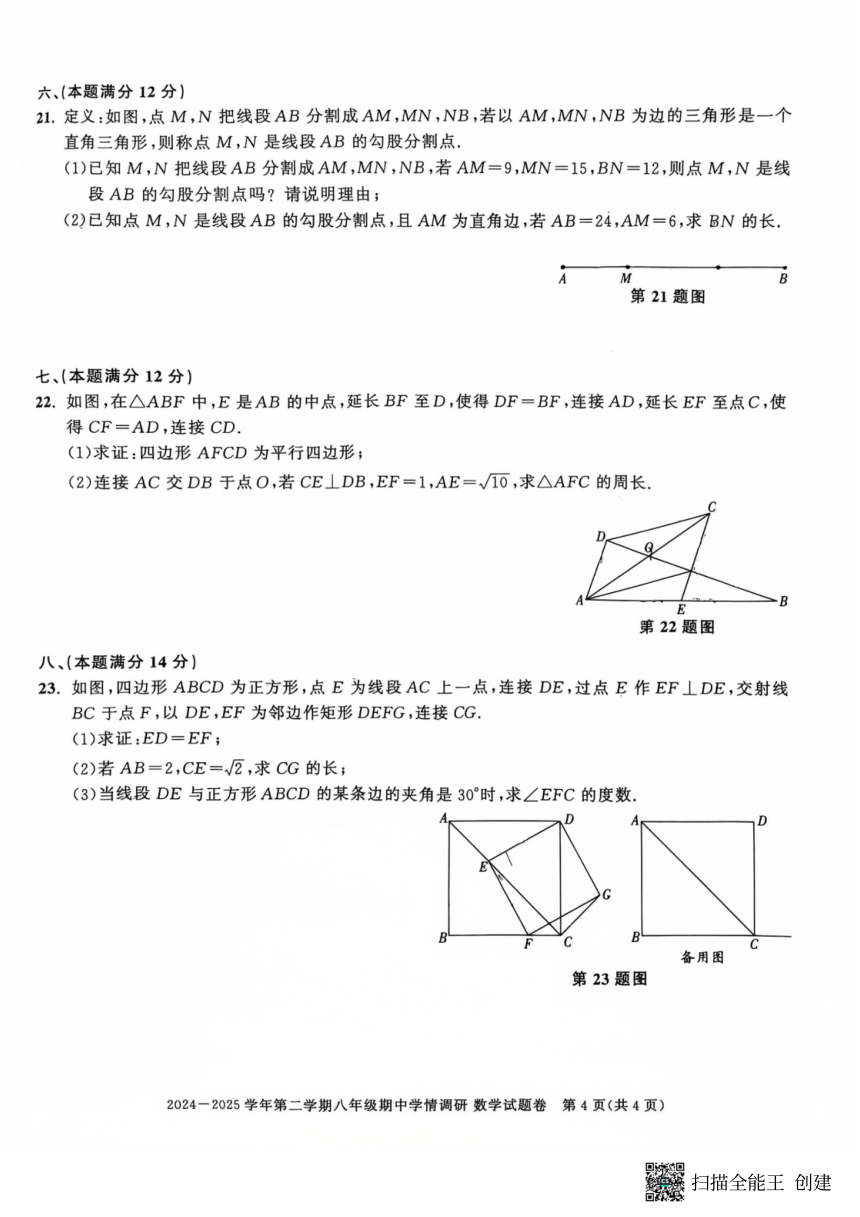
21.解:(1)是.理由如下:
∵AM2+BN2=92+122=225,MN2=152=225,∴AM2+NB2=MN2,
∴AM,MN,NB 为边的三角形是一个直角三角形,
∴点M,N 是线段AB 的勾股分割点. ……(5分)
(2)设BN=x,则MN=24-AM-BN=18-x,
①当MN 为最长线段时,由题意得MN2=AM2+BN2,
即(18-x)2=x2+36,解得x=8; ……(8分)
②当BN 为最长线段时,由题意得BN2=AM2+MN2,
即x2=36+(18-x)2,解得x=10,
综上所述,BN=8或10. ……(12分)
七、(本题满分12分)
22.解:(1)证明:∵DF=BF,∴F 是DB 的中点,
又∵E 是AB 的中点,∴EF∥AD,
∵点C 在EF 的延长线上,∴CF∥AD,
∵CF=AD,∴四边形AFCD 为平行四边形; ……(5分)
(2)∵DF=BF,AE=BE= 10,EF=1,
1
∴EF∥AD,且EF= AD,2 AB=2AE=2 10
,∴AD=2EF=2.
∵CE⊥DB 于点F,∴∠ADB=∠EFB=90°,
2
∴BD= AB2-AD2= (2 10)-22=6,
1
∴DF=BF= BD=3,∴AF= AD2+DF2= 22+322 = 13.
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 3页(共4页)
∵四边形AFCD 为平行四边形,
1 3
∴OD=OF=2DF=
,
2 OA=OC
,
3 2 5
∴OA= AD2+OD2= 22+ 2 = ,2 ∴AC=2OA=5,
∴△AFC 的周长为:AC+CF+AF=7+ 13. ……(12分)
八、(本题满分14分)
23.解:(1)证明:如图1,过点E 作EP⊥CD 于点P,EQ⊥BC 于点Q,
∵∠DCA=∠BCA,∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,
∠QEF=∠PED
在△EQF 和△EPD 中, EQ=EP ,
∠EQF=∠EPD
∴△EQF≌△EPD(ASA),∴EF=ED; ……(5分)
(2)如图2,在Rt△ABC 中,AC= 2AB=22,
∵EC= 2,∴AE=CE,
∴点F 与点C 重合,此时△DCG 是等腰直角三角形,易知CG= 2.……(8分)
(3)①当DE 与AD 的夹角为30°时,点F 在BC 边上,∠ADE=30°,
则∠CDE=90°-30°=60°,
在四边形CDEF 中,由四边形内角和定理得∠EFC=360°-90°-90°-60°=
120°; ……(11分)
②当DE 与DC 的夹角为30°时,点F 在BC 的延长线上,∠CDE=30°,如图3
所示.
∵∠HCF=∠DEF=90°,∠CHF=∠EHD,∴∠EFC=∠CDE=30°,
综上,∠EFC=120°或30°. ……(14分)
A D A D A D
G
E P
G
G E E H
B Q F C C B C FB (F)
!1 !2 !3
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 4页(共4页)
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
2024-2025学年第二学期八年级期中学情调研
数学参考答案及评分标准
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D A B C C B A
10.A
解析:如图,连接 BD,由对称性得∠DEM =∠D'EM =∠B'EN = A M D
∠BEN,∴点B,E,D 共线,即点E 在BD 上,∴当CE⊥BD 时, D′
CE 最小,∵四边形 ABCD 是矩形,∴∠BAD=90°,∴BD= E
2 1 1AB +AD2= 32+22= 13,又∵S△BCD=2BC×CD=2BD× B′
B C
, BC×CD 3×2 6 13 6 13
N
CE ∴CE= BD = =
,∴CE 的最小值为13 13 .13
故选A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11
11.29 12.25 13.2
14.(1)2;(2分)(2)19.(3分)
解析:(1)∵四边形ABDG 是平行四边形,∴AB=DG,BD=AG=7,∴AC=GD=
AB,EG=AG-AE=7-5=2,∵BC=DC,∠BDC=60°,∴△BCD 为等边三角
形,∴BC=DC=BD=7,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ABD=
60°+∠ABC,∵∠ACE=60°+∠ACB,∴∠AGD=∠ACE,在△DGE 和△ACE
∠DEG=∠AEC
中, ∠DGE=∠ACE,∴△DGE≌△ACE(AAS),∴EG=CE=2;
DG=AC
(2)如图,过点C 作CM⊥EF 于点M,∵AG//BD,∴∠CEF=∠CDB=60°,
∴∠ECM=30°,∵CE=2,∴EM=1,CM= 3,∴AM=AE-EM=5-1=4,
∴AC= AM2+CM2= 16+3= 19,∴AB=AC= 19.
B
A D
F M
E
C G
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 1页(共4页)
三、(本大题共2小题,每小题8分,满分16分)
15.解:原式=3-26+2-(5-4)
=5-26-1
=4-26. ……(8分)
16.证明:∵四边形ABCD 是平行四边形,∴∠A=∠C,
∠ABE=∠CBF
在△ABE 和△CBF 中, ∠A=∠C ,
AE=CF
∴△ABE≌△CBF(AAS),∴AB=CB,
∵四边形ABCD 是平行四边形,且AB=CB,
∴四边形ABCD 是菱形. ……(8分)
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)如图, ABCD 即为所求; ……(3分)
D C
E A B
(2)由图可得BC= 22+42=25,CE= 42+82=45,BE=10,
∴BC2+CE2=BE2,
∴△BCE 是直角三角形,∴BC⊥CE,
∵四边形ABCD 是平行四边形,∴AD//BC,∴AD⊥CE. ……(8分)
18.解:(
5 5
1)5- =5 ; ……(2分)26 26
( n n2)猜想第n 个等式为 n- 2 =n 2 . ……(5分)n +1 n +1
3 3
证明:等式左边 n +n n n n=
n2
-
+1 n2
= 2 =n 2 =等式右边,+1 n +1 n +1
故等式成立. ……(8分)
五、(本大题共2小题,每小题10分,满分20分)
19.解:如图,过点D 作DE⊥AB 于E,
则CD=BE,DE=BC=1.2米,
在Rt△ADE 中,AD=1.5米,
由勾股定理得AE= AD2-DE2= 1.52-1.22=0.9(米),
∴BE=AB-AE=2.5-0.9=1.6(米),
∴CD=BE=1.6米,
答:这名学生的身高CD 为1.6米. ……(10分)
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 2页(共4页)
A
D E
C B
20.解:(1)证明:∵四边形ABCD 是矩形,∴AD∥BC,∠ABE=90°,∴∠DAF=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠ABE=∠DFA.
∠AFD=∠EBA
在△ADF 和△EAB 中, ∠DAF=∠AEB,
AD=AE
∴△ADF≌△EAB(AAS),∴AF=BE; ……(5分)
(2)∵四边形ABCD 是矩形,BC=5,CD=3,
∴AD=BC=5,AB=CD=3,∠B=90°,
∵AD=AE,∴AE=5,∴BE= AE2-AB2= 52-32=4,
由(1)知AF=BE,∴AF=4,
∴EF=AE-AF=5-4=1. ……(10分)
六、(本题满分12分)
21.解:(1)是.理由如下:
∵AM2+BN2=92+122=225,MN2=152=225,∴AM2+NB2=MN2,
∴AM,MN,NB 为边的三角形是一个直角三角形,
∴点M,N 是线段AB 的勾股分割点. ……(5分)
(2)设BN=x,则MN=24-AM-BN=18-x,
①当MN 为最长线段时,由题意得MN2=AM2+BN2,
即(18-x)2=x2+36,解得x=8; ……(8分)
②当BN 为最长线段时,由题意得BN2=AM2+MN2,
即x2=36+(18-x)2,解得x=10,
综上所述,BN=8或10. ……(12分)
七、(本题满分12分)
22.解:(1)证明:∵DF=BF,∴F 是DB 的中点,
又∵E 是AB 的中点,∴EF∥AD,
∵点C 在EF 的延长线上,∴CF∥AD,
∵CF=AD,∴四边形AFCD 为平行四边形; ……(5分)
(2)∵DF=BF,AE=BE= 10,EF=1,
1
∴EF∥AD,且EF= AD,2 AB=2AE=2 10
,∴AD=2EF=2.
∵CE⊥DB 于点F,∴∠ADB=∠EFB=90°,
2
∴BD= AB2-AD2= (2 10)-22=6,
1
∴DF=BF= BD=3,∴AF= AD2+DF2= 22+322 = 13.
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 3页(共4页)
∵四边形AFCD 为平行四边形,
1 3
∴OD=OF=2DF=
,
2 OA=OC
,
3 2 5
∴OA= AD2+OD2= 22+ 2 = ,2 ∴AC=2OA=5,
∴△AFC 的周长为:AC+CF+AF=7+ 13. ……(12分)
八、(本题满分14分)
23.解:(1)证明:如图1,过点E 作EP⊥CD 于点P,EQ⊥BC 于点Q,
∵∠DCA=∠BCA,∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,
∠QEF=∠PED
在△EQF 和△EPD 中, EQ=EP ,
∠EQF=∠EPD
∴△EQF≌△EPD(ASA),∴EF=ED; ……(5分)
(2)如图2,在Rt△ABC 中,AC= 2AB=22,
∵EC= 2,∴AE=CE,
∴点F 与点C 重合,此时△DCG 是等腰直角三角形,易知CG= 2.……(8分)
(3)①当DE 与AD 的夹角为30°时,点F 在BC 边上,∠ADE=30°,
则∠CDE=90°-30°=60°,
在四边形CDEF 中,由四边形内角和定理得∠EFC=360°-90°-90°-60°=
120°; ……(11分)
②当DE 与DC 的夹角为30°时,点F 在BC 的延长线上,∠CDE=30°,如图3
所示.
∵∠HCF=∠DEF=90°,∠CHF=∠EHD,∴∠EFC=∠CDE=30°,
综上,∠EFC=120°或30°. ……(14分)
A D A D A D
G
E P
G
G E E H
B Q F C C B C FB (F)
!1 !2 !3
2024-2025学年第二学期八年级期中学情调研 数学参考答案及评分标准 第 4页(共4页)
同课章节目录
