湘科版(2024)七年级下册数学 5.1.2 轴对称 课件 (共27张PPT)
文档属性
| 名称 | 湘科版(2024)七年级下册数学 5.1.2 轴对称 课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 16:55:52 | ||
图片预览





文档简介
(共27张PPT)
第五章 轴对称与旋转 5.1
轴对称
湘科版(2024)七年级下册数学课件
第2课时 轴对称
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
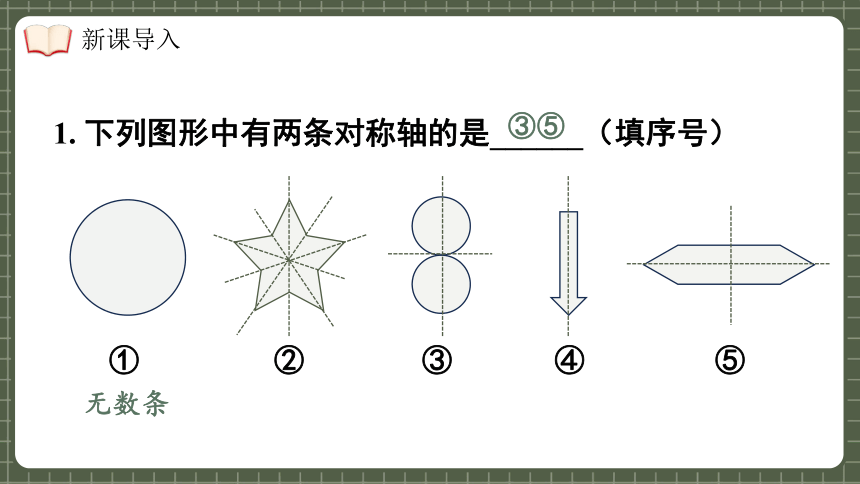
1. 下列图形中有两条对称轴的是______(填序号)
①
②
③
④
⑤
无数条
③⑤
新课导入
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个图形的特殊的位置关系
1. 都是沿着某条直线折叠后能重合
2. 可以互相转化
2. 区别与联系
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究 如图,△ABC 和△A′B′C′ 关于直线 l 对称,点 P 的对应点是 P′ ,线段 PP′ 交直线 l 于点 D. 线段 PP′ 与对称轴 l 之间有什么关系?
新课讲解
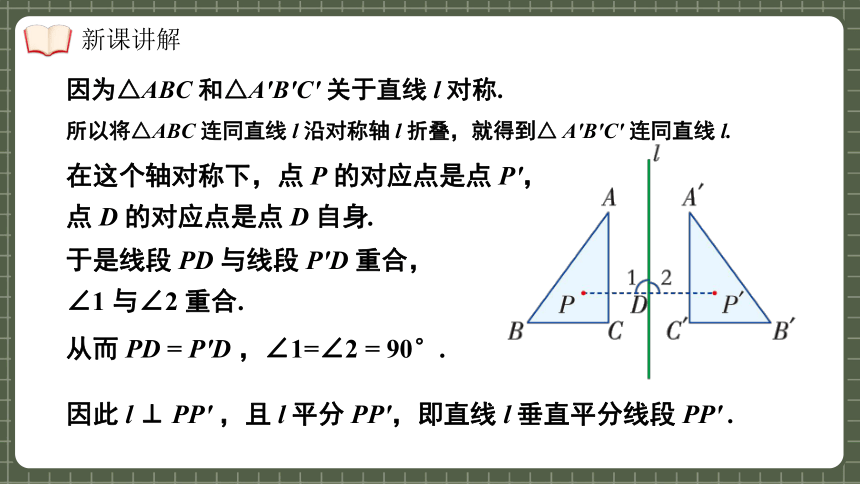
所以将△ABC 连同直线 l 沿对称轴 l 折叠,就得到△ A′B′C′ 连同直线 l.
因此 l ⊥ PP′ ,且 l 平分 PP′,即直线 l 垂直平分线段 PP′ .
因为△ABC 和△A′B′C′ 关于直线 l 对称.
在这个轴对称下,点 P 的对应点是点 P′,点 D 的对应点是点 D 自身.
于是线段 PD 与线段 P′D 重合,∠1 与∠2 重合.
从而 PD = P′D ,∠1=∠2 = 90°.
新课讲解
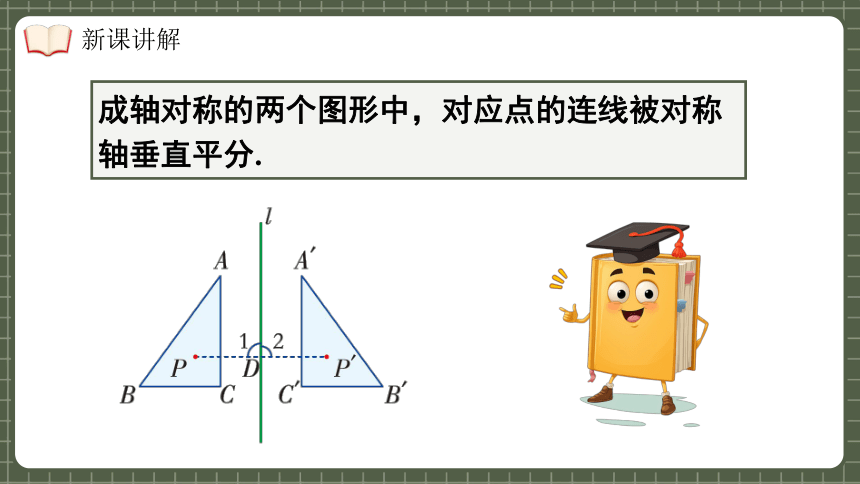
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
新课讲解
特别地,若点 P 与点 P′ 关于一条直线对称,则线段 PP′ 被这条直线垂直平分.
反过来,若线段 PP′ 被一条直线垂直平分,则点 P 与点 P′ 关于这条直线对称.
P
P′
l
新课讲解
A′B′
AB =_______,
BC =_______,
∠ABC =__________.
B′C′
∠A′B′C′
轴对称保持任意两点间距离不变,保持角的大小不变.
如图,将△ABC 沿直线 l 折叠,在这个轴对称下,点 A 的对应点是点 A′,点 B 的对应点是点 B′,点 C 的对应点是点 C′.
新课讲解
文字叙述 符号语言 图示
如图,△ABC和△A′B′C′
关于直线 MN 对称,点 A′,B′,C′分别是点 A,B,C 的对称点,AA′,BB′,CC′ 分别与 MN 交于点 E,F,G
成轴对称的两个图形中,对应
点的连线被对
称轴垂直平分
轴对称保持任意两点间距离不变,保持角的大小不变
AE =A′E,BF =B′F,
CG =C′G,MN⊥AA′,
MN⊥BB′,MN⊥CC′
AB=A′B′,BC=B′C′,
∠ABC =∠A′B′C′
新课讲解
已知直线 l 及直线外一点 P,画一点 P′, 使它与点 P 关于直线 l 对称.
作法:
1. 过点 P 作 PQ⊥l, 交 l 于点 O.
2. 在射线 OQ 上, 截取 OP′= OP.
则点 P′ 即为所求作的点.
新课讲解
已知线段 AB 和直线 l,画出线段 AB 关于直线 l 对称的图形.
作法:
1.过点 A 作直线 l 的垂线,垂足为点O,延长AO至点A′,使AO = A′O,点 A′ 就是点 A 关于直线 l 的对称点;
2.类似地,作出点 B 关于直线 l 的对称点 B′.
3.连接A′B′ .
新课讲解
已知△ABC 和直线 l,画出△ABC 关于直线 l 的对称图形.
分析 要画△ABC 关于直线 l 的对称图形,只要作出三角形的顶点 A,B,C 关于直线 l 的对称点 A′,B′ ,C′ ,
连接这些对称点即可.
新课讲解
解 (1)过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,点 A′ 就是点 A 关于直线 l 的对应点;
(2)类似地,分别作出点 B,C 关于直线 l 的对应点 B′,C′.
(3)连接 A′B′,B′C′,C′A′ 得到的△A′B′C′ 即为△ABC关于直线 l 的对称图形.
新课讲解
作已知图形关于已知直线对称的图形的一般步骤:
1. 找点(确定图形中的一些特殊点)
2. 画点(画出特殊点关于已知直线的对称点)
3. 连线(连接对称点)
新课讲解
画好△A′B′C′ 后,若将纸沿直线 l 折叠,两个三角形会重合吗?
折叠动画
成轴对称的两个图形的形状、大小完全相同,即两个图形的对应线段相等,对应角相等,面积相等,周长相等.
新课讲解
先过直线 l 外一点分别画直线 l 的垂线段与斜线段,再利用轴对称变换说明垂线段最短,并将结果与同学交流.
l
P
新课讲解
1. 已知直线 AB 和直线 l 相交于点 O,画出直线 AB
关于直线 l 的对称图形.
l
O
A
B
A′
B′
课堂练习
2. 如图,△ABC 与△A′B′C′ 关于直线 MN 成轴对称. 指出它们的对应顶点,并分别找出三对相等的边和相等的角.
A′
A
B′
C′
B
C
N
M
A 和 A′
B 和 B′
C 和 C′
AB =A′B′
BC =B′C′
AC =A′C′
∠ABC =∠A′B′C′
∠BCA =∠B′C′A′
∠BAC =∠B′A′C′
课堂练习
1. 如图,若△ABC 与△A′B′C′ 关于直线 MN 对称,线段 BB′
交直线 MN 于点 O,则下列说法不一定正确的是( )
A. AC =A′C′ B. BO =B′O
C. AA′⊥ MN D. AB∥B′C′
D
课堂练习
2. 下面是四位同学画△ABC 关于直线 MN 的对称图形的
方法,其中正确的是( )
B
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
对应点的连线被对称轴垂直平分
轴对称变换
轴对称的性质
作图方法
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
第五章 轴对称与旋转 5.1
轴对称
湘科版(2024)七年级下册数学课件
第2课时 轴对称
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 下列图形中有两条对称轴的是______(填序号)
①
②
③
④
⑤
无数条
③⑤
新课导入
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个图形的特殊的位置关系
1. 都是沿着某条直线折叠后能重合
2. 可以互相转化
2. 区别与联系
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究 如图,△ABC 和△A′B′C′ 关于直线 l 对称,点 P 的对应点是 P′ ,线段 PP′ 交直线 l 于点 D. 线段 PP′ 与对称轴 l 之间有什么关系?
新课讲解
所以将△ABC 连同直线 l 沿对称轴 l 折叠,就得到△ A′B′C′ 连同直线 l.
因此 l ⊥ PP′ ,且 l 平分 PP′,即直线 l 垂直平分线段 PP′ .
因为△ABC 和△A′B′C′ 关于直线 l 对称.
在这个轴对称下,点 P 的对应点是点 P′,点 D 的对应点是点 D 自身.
于是线段 PD 与线段 P′D 重合,∠1 与∠2 重合.
从而 PD = P′D ,∠1=∠2 = 90°.
新课讲解
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
新课讲解
特别地,若点 P 与点 P′ 关于一条直线对称,则线段 PP′ 被这条直线垂直平分.
反过来,若线段 PP′ 被一条直线垂直平分,则点 P 与点 P′ 关于这条直线对称.
P
P′
l
新课讲解
A′B′
AB =_______,
BC =_______,
∠ABC =__________.
B′C′
∠A′B′C′
轴对称保持任意两点间距离不变,保持角的大小不变.
如图,将△ABC 沿直线 l 折叠,在这个轴对称下,点 A 的对应点是点 A′,点 B 的对应点是点 B′,点 C 的对应点是点 C′.
新课讲解
文字叙述 符号语言 图示
如图,△ABC和△A′B′C′
关于直线 MN 对称,点 A′,B′,C′分别是点 A,B,C 的对称点,AA′,BB′,CC′ 分别与 MN 交于点 E,F,G
成轴对称的两个图形中,对应
点的连线被对
称轴垂直平分
轴对称保持任意两点间距离不变,保持角的大小不变
AE =A′E,BF =B′F,
CG =C′G,MN⊥AA′,
MN⊥BB′,MN⊥CC′
AB=A′B′,BC=B′C′,
∠ABC =∠A′B′C′
新课讲解
已知直线 l 及直线外一点 P,画一点 P′, 使它与点 P 关于直线 l 对称.
作法:
1. 过点 P 作 PQ⊥l, 交 l 于点 O.
2. 在射线 OQ 上, 截取 OP′= OP.
则点 P′ 即为所求作的点.
新课讲解
已知线段 AB 和直线 l,画出线段 AB 关于直线 l 对称的图形.
作法:
1.过点 A 作直线 l 的垂线,垂足为点O,延长AO至点A′,使AO = A′O,点 A′ 就是点 A 关于直线 l 的对称点;
2.类似地,作出点 B 关于直线 l 的对称点 B′.
3.连接A′B′ .
新课讲解
已知△ABC 和直线 l,画出△ABC 关于直线 l 的对称图形.
分析 要画△ABC 关于直线 l 的对称图形,只要作出三角形的顶点 A,B,C 关于直线 l 的对称点 A′,B′ ,C′ ,
连接这些对称点即可.
新课讲解
解 (1)过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,点 A′ 就是点 A 关于直线 l 的对应点;
(2)类似地,分别作出点 B,C 关于直线 l 的对应点 B′,C′.
(3)连接 A′B′,B′C′,C′A′ 得到的△A′B′C′ 即为△ABC关于直线 l 的对称图形.
新课讲解
作已知图形关于已知直线对称的图形的一般步骤:
1. 找点(确定图形中的一些特殊点)
2. 画点(画出特殊点关于已知直线的对称点)
3. 连线(连接对称点)
新课讲解
画好△A′B′C′ 后,若将纸沿直线 l 折叠,两个三角形会重合吗?
折叠动画
成轴对称的两个图形的形状、大小完全相同,即两个图形的对应线段相等,对应角相等,面积相等,周长相等.
新课讲解
先过直线 l 外一点分别画直线 l 的垂线段与斜线段,再利用轴对称变换说明垂线段最短,并将结果与同学交流.
l
P
新课讲解
1. 已知直线 AB 和直线 l 相交于点 O,画出直线 AB
关于直线 l 的对称图形.
l
O
A
B
A′
B′
课堂练习
2. 如图,△ABC 与△A′B′C′ 关于直线 MN 成轴对称. 指出它们的对应顶点,并分别找出三对相等的边和相等的角.
A′
A
B′
C′
B
C
N
M
A 和 A′
B 和 B′
C 和 C′
AB =A′B′
BC =B′C′
AC =A′C′
∠ABC =∠A′B′C′
∠BCA =∠B′C′A′
∠BAC =∠B′A′C′
课堂练习
1. 如图,若△ABC 与△A′B′C′ 关于直线 MN 对称,线段 BB′
交直线 MN 于点 O,则下列说法不一定正确的是( )
A. AC =A′C′ B. BO =B′O
C. AA′⊥ MN D. AB∥B′C′
D
课堂练习
2. 下面是四位同学画△ABC 关于直线 MN 的对称图形的
方法,其中正确的是( )
B
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
对应点的连线被对称轴垂直平分
轴对称变换
轴对称的性质
作图方法
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
