2.2导数的几何意义课件(共25张PPT)-高二下学期数学北师大版选择性必修二册
文档属性
| 名称 | 2.2导数的几何意义课件(共25张PPT)-高二下学期数学北师大版选择性必修二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 860.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 18:25:59 | ||
图片预览







文档简介
(共25张PPT)
2.2导数的几何意义
北师大版选择性必修二第二章第二节
适用地区:河南省南阳市高二年级
通过图像理解导数的几何意义
会利用导数求曲线上某点处的切线方程.
通过图象理解导数的几何意义,培养直观想象能力
通过导数几何意义的应用,提升数学运算、数形结合及逻
辑推理素养.
学 习
01.
02.
03.
04.
知识点一
导数的几何意义
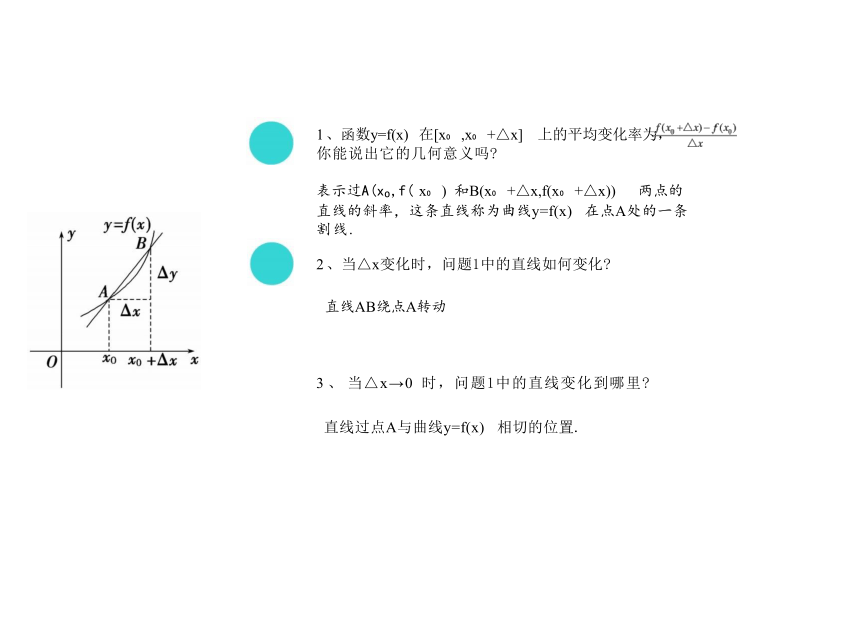
1 、函数y=f(x) 在[x ,x +△x] 上的平均变化率为, 你能说出它的几何意义吗
表示过A(x ,f( x ) 和B(x +△x,f(x +△x)) 两点的
直线的斜率,这条直线称为曲线y=f(x) 在点A处的一条 割线.
2 、当△x变化时,问题1中的直线如何变化
直线AB绕点A转动
3 、 当△x→0 时,问题1中的直线变化到哪里
直线过点A与曲线y=f(x) 相切的位置.
知识框架构建
割线的定义 切线的定义 导数的定义
1. 割线的定义
设函数y=f(x) 的图象是一条光滑的曲线,且函数y=f(x) 在 区间[x ,x +△x] 的平均变化率为 ,
它是经过A(x ,f(x )) 和B(x +△x,f(x +△x)) 两点的直线的 _,这条直线称为曲线y=f(x) 在点A处的一条割线。
斜率
点A
2 . 切线的定义
如图,当△x 趋于0时,点B将沿着曲线y=f(x) 趋于
制线AB将绕点A转动趋于直线l, 称直线为曲线y=f(x) 在_
点 A 的切线,或称直线和曲线y=f(x) 在点A处相切.
B B
A
y 个
O
Xo x
y=f(x)
l
函数y=f(x) 在x, 处的导数f(x ), 是曲
线y=f(x) 在 点(x ,f(x ) 处 的 切线的斜率 , 函 数y=f(x) 在 x 处
切线的斜率 反映了导数的几何意
义 .
3、导数的定义
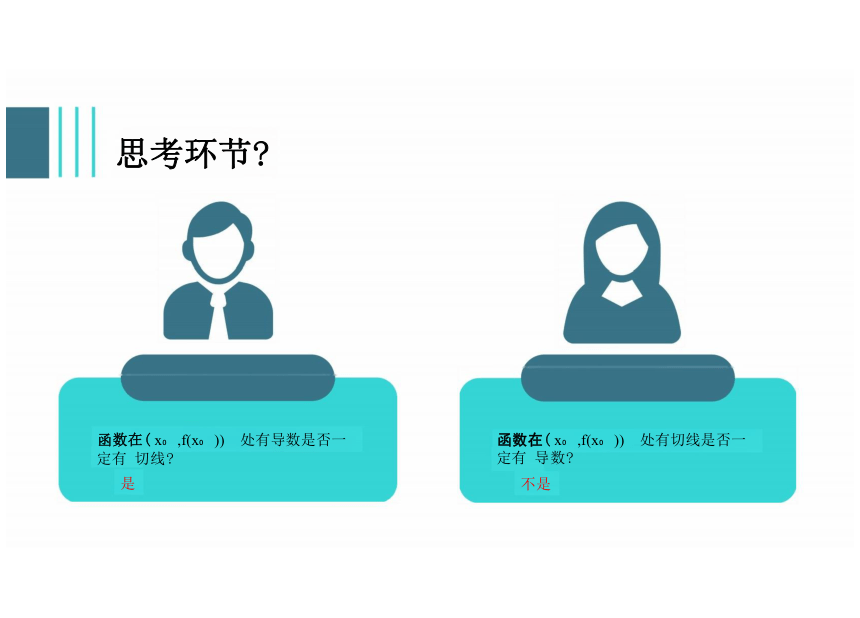
函数在( x ,f(x )) 处有切线是否一定有 导数
不是
函数在( x ,f(x )) 处有导数是否一定有 切线
是
思考环节
典例试炼
例1、已知函数f(x) 的图象如图所示,则下列选项正确的是
C.f(2)>f(3)-f(2)
D.f(2)>0
(C)
方法归纳
X
导数的几何意义就是切线的斜率,所以比较在_处导数大小的问题可以用数形结合思想 )点的切线,通过观察倾斜角的大小来解决.
y
1 、已知函数y=f(x) 的部分图象如图所示,其中A(1,f(1)),B(2,f(2))
A.f(1)>f(2)>f(4)
B.f(4)>f(2)>f(1)
C.f(4)>f(1)>f(2)
D.f(1)>f(4)>f(2)
A
0
B
吉论正确的是( )
C
x
变式训练
B
变式训练
A、〔 〕 B 、〔 〕 C、〔0,1〕 D 、〔
A
1 ( ) 〕
切线倾斜角的取值范围为(0,),则!
坐标的取
上的
点,且曲线C在 1 , 0
2 、设p是曲
知识点二
求切线方程
例2、已知曲线 9 求曲线在点P(2,4) 处的切线方程.
解:因为点P(2,4) 在曲线
所以曲线在点P(2,4) 处切线的斜率为
所以曲线在点P(2,4) 处的切线方程为y-4=4(x-2), 即4x-y-4=0.
变式训练
1、设1为曲线C: 在点(1,0)处的切线,求l的方程。
解 :
f'(x)=1, 直 线l的 方 程 为y= x-1
变式训练
2 、 求过点(2,0)且与曲线 y=x 相切的直线方程。
变式训练
2、求过点(2,0)且与曲线 y=x 相切的直线方程。
解:点(2,0)不在曲线 y=x 上,可设切点坐标为(x ,x ),则所求直线的斜率
得 -x =3x 。 (2-x ), 解得 x =0 或x =3. 所求的直线方程为 y=0
或 者 2 7x-y-54=0
,切线方程为 y-x 。 =3x 。 (x-x ), 点(2,0)在切线上,
巩固练习
1、曲线 处的切线的倾斜角是 ( D 丁 丁 丁 3π
A、 B、 C、 D、
6 4 3 4
2 、设 f(x)=xln x, 若 f'(x )=2, 则 xo= ( B)
A、e B、e c 、In2 D、In 2 2
巩固练习
3、过点( - 1,0)做抛物线 y=x +x+1 的切线,其则中一条切线 的方程为 ( D )
A 、2x+y+2=0 B 、3x-y+3=0
C 、x+y+1=0 D、 x-y+1=0
4 、在抛物线 y=x 上依次取两点,它们的横坐标分别为
x =1,x =3, 若抛物线上过点P的切线与过这两点的割线平行,
则点P的坐标为 ( 2,4 )
巩固练习
课后作业
5 、 若直线 y=kx
与曲线 y=x -3x +2x
相切, 求 k 的 值
5、解:设直线与曲线相切于点 (x ,yo),∵y'=3x -6x+2
∴切点 (x ,yo) 处的切线的斜率是 f(x )=3x, -6x,+2, 又
∵y =kx 过原点,故切线的斜率为
又∵点 (x ,y。)在曲线 y=x -3x +2x 上,
, ∴ xo=0 或
6 、已知函数 f(x)=ax +2In(2-x),a∈R, 设曲线 y=f(x)
在点(1,f(1)) 处的切线为 l, 若 l 与圆C: 相切,求 a
的值
6、解:由题意知: f(1)=a, (x<2)
∴ k=f'(1)=2a-2,∴ 直线 的 斜 率 为 2a-2 且过点(1,a)
∴l 的 方 程 为 2(a-1)x-y+2-a=0
∵l 与圆相切,
解得
2.2导数的几何意义
北师大版选择性必修二第二章第二节
适用地区:河南省南阳市高二年级
通过图像理解导数的几何意义
会利用导数求曲线上某点处的切线方程.
通过图象理解导数的几何意义,培养直观想象能力
通过导数几何意义的应用,提升数学运算、数形结合及逻
辑推理素养.
学 习
01.
02.
03.
04.
知识点一
导数的几何意义
1 、函数y=f(x) 在[x ,x +△x] 上的平均变化率为, 你能说出它的几何意义吗
表示过A(x ,f( x ) 和B(x +△x,f(x +△x)) 两点的
直线的斜率,这条直线称为曲线y=f(x) 在点A处的一条 割线.
2 、当△x变化时,问题1中的直线如何变化
直线AB绕点A转动
3 、 当△x→0 时,问题1中的直线变化到哪里
直线过点A与曲线y=f(x) 相切的位置.
知识框架构建
割线的定义 切线的定义 导数的定义
1. 割线的定义
设函数y=f(x) 的图象是一条光滑的曲线,且函数y=f(x) 在 区间[x ,x +△x] 的平均变化率为 ,
它是经过A(x ,f(x )) 和B(x +△x,f(x +△x)) 两点的直线的 _,这条直线称为曲线y=f(x) 在点A处的一条割线。
斜率
点A
2 . 切线的定义
如图,当△x 趋于0时,点B将沿着曲线y=f(x) 趋于
制线AB将绕点A转动趋于直线l, 称直线为曲线y=f(x) 在_
点 A 的切线,或称直线和曲线y=f(x) 在点A处相切.
B B
A
y 个
O
Xo x
y=f(x)
l
函数y=f(x) 在x, 处的导数f(x ), 是曲
线y=f(x) 在 点(x ,f(x ) 处 的 切线的斜率 , 函 数y=f(x) 在 x 处
切线的斜率 反映了导数的几何意
义 .
3、导数的定义
函数在( x ,f(x )) 处有切线是否一定有 导数
不是
函数在( x ,f(x )) 处有导数是否一定有 切线
是
思考环节
典例试炼
例1、已知函数f(x) 的图象如图所示,则下列选项正确的是
C.f(2)>f(3)-f(2)
D.f(2)>0
(C)
方法归纳
X
导数的几何意义就是切线的斜率,所以比较在_处导数大小的问题可以用数形结合思想 )点的切线,通过观察倾斜角的大小来解决.
y
1 、已知函数y=f(x) 的部分图象如图所示,其中A(1,f(1)),B(2,f(2))
A.f(1)>f(2)>f(4)
B.f(4)>f(2)>f(1)
C.f(4)>f(1)>f(2)
D.f(1)>f(4)>f(2)
A
0
B
吉论正确的是( )
C
x
变式训练
B
变式训练
A、〔 〕 B 、〔 〕 C、〔0,1〕 D 、〔
A
1 ( ) 〕
切线倾斜角的取值范围为(0,),则!
坐标的取
上的
点,且曲线C在 1 , 0
2 、设p是曲
知识点二
求切线方程
例2、已知曲线 9 求曲线在点P(2,4) 处的切线方程.
解:因为点P(2,4) 在曲线
所以曲线在点P(2,4) 处切线的斜率为
所以曲线在点P(2,4) 处的切线方程为y-4=4(x-2), 即4x-y-4=0.
变式训练
1、设1为曲线C: 在点(1,0)处的切线,求l的方程。
解 :
f'(x)=1, 直 线l的 方 程 为y= x-1
变式训练
2 、 求过点(2,0)且与曲线 y=x 相切的直线方程。
变式训练
2、求过点(2,0)且与曲线 y=x 相切的直线方程。
解:点(2,0)不在曲线 y=x 上,可设切点坐标为(x ,x ),则所求直线的斜率
得 -x =3x 。 (2-x ), 解得 x =0 或x =3. 所求的直线方程为 y=0
或 者 2 7x-y-54=0
,切线方程为 y-x 。 =3x 。 (x-x ), 点(2,0)在切线上,
巩固练习
1、曲线 处的切线的倾斜角是 ( D 丁 丁 丁 3π
A、 B、 C、 D、
6 4 3 4
2 、设 f(x)=xln x, 若 f'(x )=2, 则 xo= ( B)
A、e B、e c 、In2 D、In 2 2
巩固练习
3、过点( - 1,0)做抛物线 y=x +x+1 的切线,其则中一条切线 的方程为 ( D )
A 、2x+y+2=0 B 、3x-y+3=0
C 、x+y+1=0 D、 x-y+1=0
4 、在抛物线 y=x 上依次取两点,它们的横坐标分别为
x =1,x =3, 若抛物线上过点P的切线与过这两点的割线平行,
则点P的坐标为 ( 2,4 )
巩固练习
课后作业
5 、 若直线 y=kx
与曲线 y=x -3x +2x
相切, 求 k 的 值
5、解:设直线与曲线相切于点 (x ,yo),∵y'=3x -6x+2
∴切点 (x ,yo) 处的切线的斜率是 f(x )=3x, -6x,+2, 又
∵y =kx 过原点,故切线的斜率为
又∵点 (x ,y。)在曲线 y=x -3x +2x 上,
, ∴ xo=0 或
6 、已知函数 f(x)=ax +2In(2-x),a∈R, 设曲线 y=f(x)
在点(1,f(1)) 处的切线为 l, 若 l 与圆C: 相切,求 a
的值
6、解:由题意知: f(1)=a, (x<2)
∴ k=f'(1)=2a-2,∴ 直线 的 斜 率 为 2a-2 且过点(1,a)
∴l 的 方 程 为 2(a-1)x-y+2-a=0
∵l 与圆相切,
解得
同课章节目录
