6.3.1二项式定理 课件(共24张PPT)-高二下学期数学人教A版选择性必修第三册
文档属性
| 名称 | 6.3.1二项式定理 课件(共24张PPT)-高二下学期数学人教A版选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:02:01 | ||
图片预览




文档简介
(共24张PPT)
6.3.1二项式定理
一、情境引入
7.07365≈37.8 0.99365≈0.03
7.02365≈7377.4 0.98365≈0.0006
2
· 牛顿在1664-1665年
间发现了二项式定理
(a+b)"=
二、探究归纳
(a+b) =a +2ab+b
(a+b) =a +3a b+3ab +b
(a+b) =
(a+b)"=
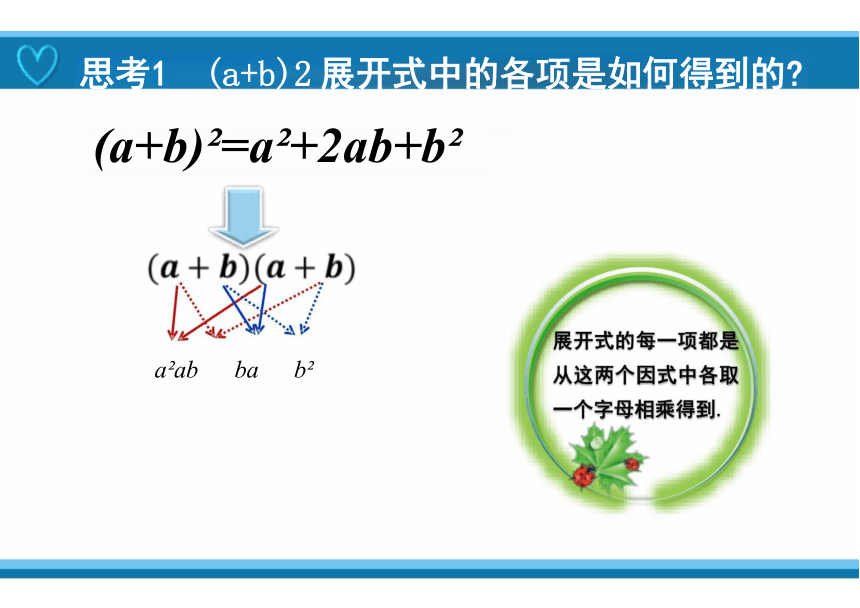
思考1 (a+b)2 展开式中的各项是如何得到的
(a+b) =a +2ab+b
a ab ba b
C2 a
C ab
C b
=a +2ab+b
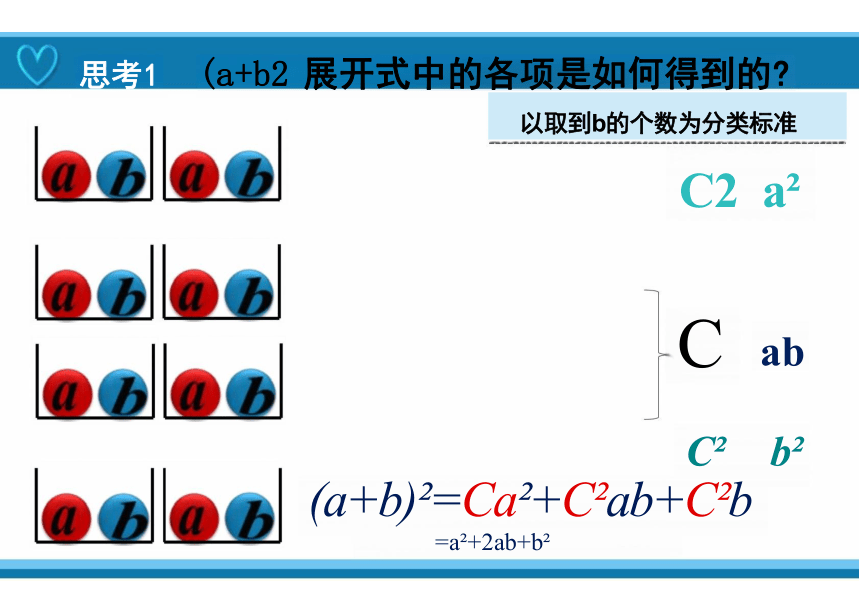
思考1 (a+b2 展开式中的各项是如何得到的
(a+b) =Ca +C ab+C b
以取到b的个数为分类标准
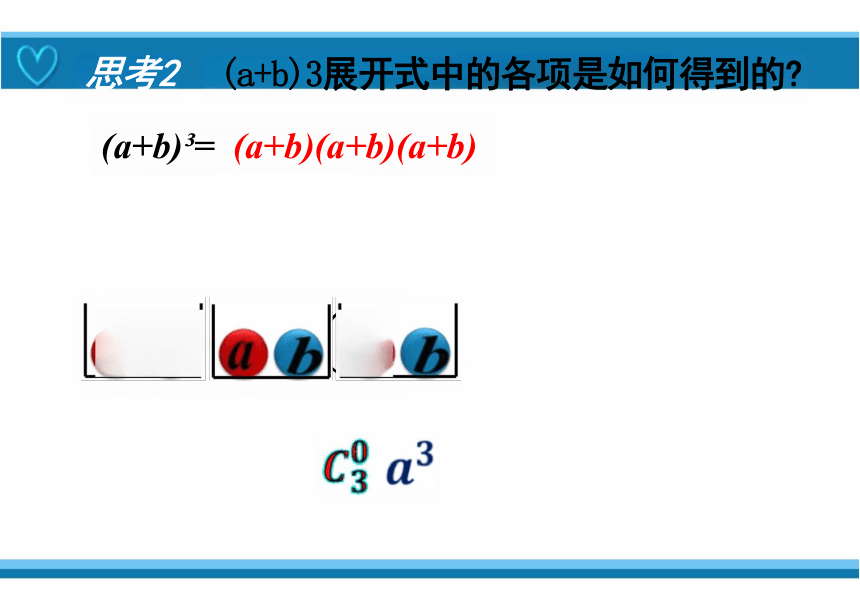
思考2 (a+b)3展开式中的各项是如何得到的
(a+b) = (a+b)(a+b)(a+b)
@b@b@
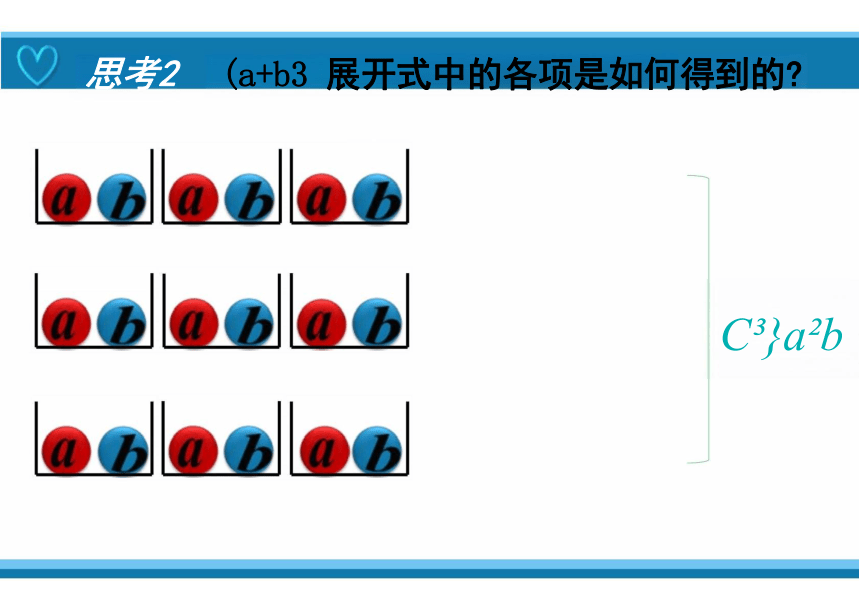
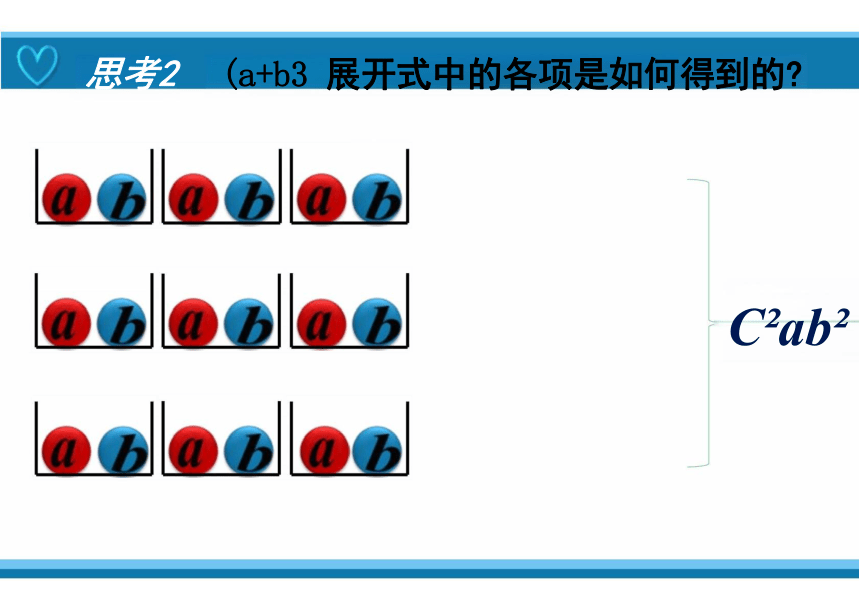
思考2 (a+b3 展开式中的各项是如何得到的
C }a b
思考2 (a+b3 展开式中的各项是如何得到的
C ab
思考2 (a+b)3展开式中的各项是如何得到的
a
a a a C3 a
C3a b(a+b)=c a +C a b+C ab +C b
@ C ab =a +3a b+3ab +b
b C b
L
1
思考2 (a+b3 展开式中的各项是如何得到的
(a+b) =(a+b)(a+b)(a+b)(a+b)
探 究 :
(1)(a+b) 展开后各项形式分别是什么
a a b a b ab b
(2)你能分析说明各项前的系数吗
(a+b) =Ca +C+a b+C a b +Ciab +b
思考3 (a+b)4 展开式中的各项是如何得到的
思考4 (a+bn(n∈N*) 展开式中的各项是如何
(a+b) =
猜 想 :
(a+b)"= n 十 … +C"b"(n∈N)
三 、建构 数学
(a+b)"=(a+b)(a+b)…(a+b
n
a a
a n个 Cn an
C1 an-1
a a ch an-
bb k个 b Cbn
(a+b)"=Cd"+Ca-b+…+Ca"kb +…+Cb"(n∈N)
二项式定理
三 、建构数学
次数规律
· 各项的次数
均为n;
· 各项里a的 次数由n减 小到0,b的 次数由0增 大到n.
项数规律
· 两项和的n
次幂的展
开式共有
n+1个项 .
三、认识二项式定理
通项公式
TI=C"a b".
(k=0120n)
系数规律
C,CC 。
oo C”.
例 已知(1+2x)
(1)求它的展开式; (2)求它的展开式中第4项;
(1+2x) =C(2x)°+C (2x) +C (2x) +C (2x)
+C (2x) +C,(2x) +C (2x) +C (2x)
3)+求它的展开式皮含 项的系数及二项式系数i8x7
四应用体验
例2 (1)求(1+2x) 的展开式的第4项的系数; 一个二项展 开式的某一项
(2)求 的展开式中x 的系数 . 的二项式系数 与这一系数是
解:(1)由通项公式,可得 两个不同的概
T =T3+1=C (2x) =280x . 念
∴(1+2x) 的展开式的第4项的系数是280.
(2)由通项公式,可得
设3-k=2, 解得k=1.
∴x 的系数是(- 1)×2 ×C =-192.
例题讲解
例2. (1) 的展开式中,常数项是() .
B C. 口
答案:D.
解:(1) 展开式的通项
令 1 2 - 3r=0, 解 得r=4.
所以常数项
,
解:(2) 的展开式的通项
(r=0,1,2, …,8), 使Tr+1为有理项,r 必须是4的倍数,
所以r=0,4,8, 故共有3个有理项,分别
例2. (2). 的展开式中的有理项.
巩固训练
5.在(x -1)(x-2)(x-3)(x-4) (x-5) 的展开式中,含x 的项的系数是 ●
解:含x 的项是由5个括号中任意4个括号各取出1个x, 剩余1个括号取出常 数相乘得到的,故含x 的项的系数是
(-1)+(-2)+ (-3)+ (-4)+(-5)=-15.
1、 (1)化简(x-1) +4(x-1) +6(x-1) +4(x-1)+1 得(A )
A.x4 B.(x-1)
C.(x+1) D.x
(2)3Cn+9C +27C + …+3"Cn= 4"-1 (n∈N).
解析:3Cn+9C +27C +…+3"Cn
=Cn+3Cn+9C +27C +…+3"Cn-1
=(1+3)"-1=4"-1.
拓展练习
二项式定理(项和系数)
运用计数原理推导二项式定理(从特殊到一般,归纳推理)
运用二项式定理解决数学问题(化归思想)
在具体情境中运用二项式定理(数学服务生活)
五、课堂小结
发现问题-探索规律- 总结规律-应用规律
数学抽象
逻辑推理
数学运算
数学建模
核心素养
6.3.1二项式定理
一、情境引入
7.07365≈37.8 0.99365≈0.03
7.02365≈7377.4 0.98365≈0.0006
2
· 牛顿在1664-1665年
间发现了二项式定理
(a+b)"=
二、探究归纳
(a+b) =a +2ab+b
(a+b) =a +3a b+3ab +b
(a+b) =
(a+b)"=
思考1 (a+b)2 展开式中的各项是如何得到的
(a+b) =a +2ab+b
a ab ba b
C2 a
C ab
C b
=a +2ab+b
思考1 (a+b2 展开式中的各项是如何得到的
(a+b) =Ca +C ab+C b
以取到b的个数为分类标准
思考2 (a+b)3展开式中的各项是如何得到的
(a+b) = (a+b)(a+b)(a+b)
@b@b@
思考2 (a+b3 展开式中的各项是如何得到的
C }a b
思考2 (a+b3 展开式中的各项是如何得到的
C ab
思考2 (a+b)3展开式中的各项是如何得到的
a
a a a C3 a
C3a b(a+b)=c a +C a b+C ab +C b
@ C ab =a +3a b+3ab +b
b C b
L
1
思考2 (a+b3 展开式中的各项是如何得到的
(a+b) =(a+b)(a+b)(a+b)(a+b)
探 究 :
(1)(a+b) 展开后各项形式分别是什么
a a b a b ab b
(2)你能分析说明各项前的系数吗
(a+b) =Ca +C+a b+C a b +Ciab +b
思考3 (a+b)4 展开式中的各项是如何得到的
思考4 (a+bn(n∈N*) 展开式中的各项是如何
(a+b) =
猜 想 :
(a+b)"= n 十 … +C"b"(n∈N)
三 、建构 数学
(a+b)"=(a+b)(a+b)…(a+b
n
a a
a n个 Cn an
C1 an-1
a a ch an-
bb k个 b Cbn
(a+b)"=Cd"+Ca-b+…+Ca"kb +…+Cb"(n∈N)
二项式定理
三 、建构数学
次数规律
· 各项的次数
均为n;
· 各项里a的 次数由n减 小到0,b的 次数由0增 大到n.
项数规律
· 两项和的n
次幂的展
开式共有
n+1个项 .
三、认识二项式定理
通项公式
TI=C"a b".
(k=0120n)
系数规律
C,CC 。
oo C”.
例 已知(1+2x)
(1)求它的展开式; (2)求它的展开式中第4项;
(1+2x) =C(2x)°+C (2x) +C (2x) +C (2x)
+C (2x) +C,(2x) +C (2x) +C (2x)
3)+求它的展开式皮含 项的系数及二项式系数i8x7
四应用体验
例2 (1)求(1+2x) 的展开式的第4项的系数; 一个二项展 开式的某一项
(2)求 的展开式中x 的系数 . 的二项式系数 与这一系数是
解:(1)由通项公式,可得 两个不同的概
T =T3+1=C (2x) =280x . 念
∴(1+2x) 的展开式的第4项的系数是280.
(2)由通项公式,可得
设3-k=2, 解得k=1.
∴x 的系数是(- 1)×2 ×C =-192.
例题讲解
例2. (1) 的展开式中,常数项是() .
B C. 口
答案:D.
解:(1) 展开式的通项
令 1 2 - 3r=0, 解 得r=4.
所以常数项
,
解:(2) 的展开式的通项
(r=0,1,2, …,8), 使Tr+1为有理项,r 必须是4的倍数,
所以r=0,4,8, 故共有3个有理项,分别
例2. (2). 的展开式中的有理项.
巩固训练
5.在(x -1)(x-2)(x-3)(x-4) (x-5) 的展开式中,含x 的项的系数是 ●
解:含x 的项是由5个括号中任意4个括号各取出1个x, 剩余1个括号取出常 数相乘得到的,故含x 的项的系数是
(-1)+(-2)+ (-3)+ (-4)+(-5)=-15.
1、 (1)化简(x-1) +4(x-1) +6(x-1) +4(x-1)+1 得(A )
A.x4 B.(x-1)
C.(x+1) D.x
(2)3Cn+9C +27C + …+3"Cn= 4"-1 (n∈N).
解析:3Cn+9C +27C +…+3"Cn
=Cn+3Cn+9C +27C +…+3"Cn-1
=(1+3)"-1=4"-1.
拓展练习
二项式定理(项和系数)
运用计数原理推导二项式定理(从特殊到一般,归纳推理)
运用二项式定理解决数学问题(化归思想)
在具体情境中运用二项式定理(数学服务生活)
五、课堂小结
发现问题-探索规律- 总结规律-应用规律
数学抽象
逻辑推理
数学运算
数学建模
核心素养
