5.3.2 函数的极值与最大(小)值(第一课时)课件(共17张PPT)-高二下学期数学人教A版选择性必修第二册
文档属性
| 名称 | 5.3.2 函数的极值与最大(小)值(第一课时)课件(共17张PPT)-高二下学期数学人教A版选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:06:44 | ||
图片预览





文档简介
(共17张PPT)
5.3.2 函数的极值与最大 (小)值(第一课时)
学习目标
1.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.
2.能利用导数求某些函数的极大值、极小值。
3.过理解函数的极值及其应用导数的求解过程,发展直观想象与数学运算素养。 教学重难点
教学重点:理解函数极小值点、极大值点和极大值、极小值。
教学难点:理解函数极小值点、极大值点和极大值、极小值概念。
复习回顾
函数单调性与导数的关系:
设函数y=f(x) 在区间(a,b) 内的导数为f'(x).
如果f'(x)>0, 则f(x)在(a,b)内为单调递增;
如果f'(x)<0,f(x) 在(a,b)内为单调递减;
如果f'(x)=0, 则f(x)在(a,b)内为常数函数;
反 之 ,
如果f(x)在(a,b)内为增函数,则f'(x)≥0 在(a,b)内恒成立;
如果f(x)在(a,b)内为减函数,则f'(x)≤0 在(a,b)内恒成立.
在用导数研究函数的单调性时,我们发现利用导数的正负可以 判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函 数有什么性质呢
这是江西庐山群山叠嶂的景象。
苏轼在《题西林壁》中这样写道:
“横看成岭侧成峰,远近高低各不
同”,描述的就是庐山的高低起伏, 错落有致。在群山之中,各个山峰的 顶端,虽然不是群山的最高处,但它 却是其附近的最高点。
在数学上,这种现象如何来刻画呢
即当t在a的附近从小到大经过a时 ,h'(t)先正后 负,且h'(t) 连续变化,于是有h'(a)=0.
(1) 对于一般的函数y=f(x), 是否也有同样的性质
观察下图,我们发现,当 t=a 时,高台跳水运动员距水面的高度最大.
函 数h(t) 在此点的导数是多少呢 此点附近的图象有什么特点 相应地, 导数的符号有什么变化规律
当tk0;
当t>a时,函数h(t)单调递减, h'(t)<0.
这就是说,在t=a 附近,函数值先增后减,
由图可以看出,h'(a)=0;
在t=a的附近,
放大t=a附近的图象,如图0(2)所示.
单调性递减,
这些点附近,y=f(x) 的导数的符号有什么规律
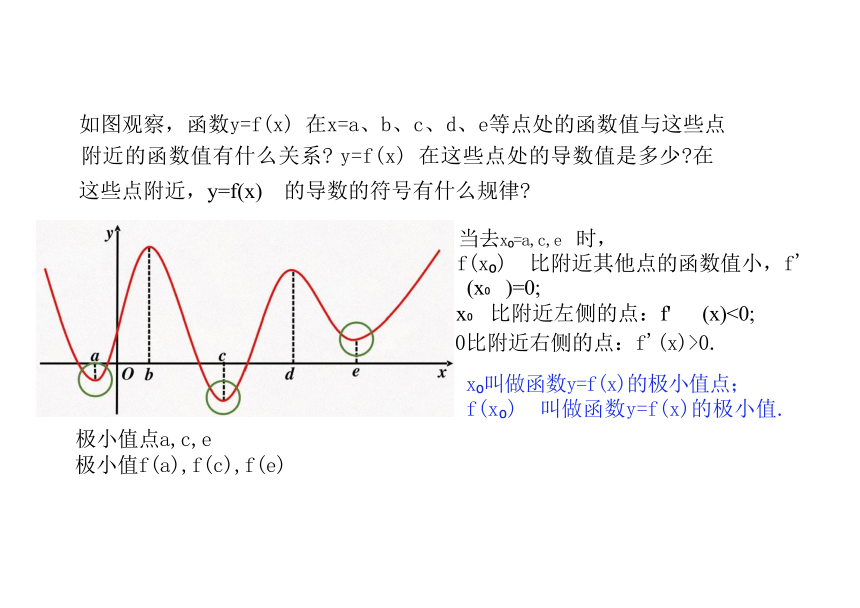
当去x =a,c,e 时,
f(x ) 比附近其他点的函数值小,f' (x )=0;
x 比附近左侧的点:f' (x)<0;
0比附近右侧的点:f'(x)>0.
x 叫做函数y=f(x)的极小值点;
f(x ) 叫做函数y=f(x)的极小值.
极小值点a,c,e
极小值f(a),f(c),f(e)
如图观察,函数y=f(x) 在x=a、b、c、d、e等点处的函数值与这些点
附近的函数值有什么关系 y=f(x) 在这些点处的导数值是多少 在
如图观察,函数y=f(x) 在x=a 、b 、c 、d 、e 等点处的函数值与这些点
附近的函数值有什么关系 y=f(x) 在这些点处的导数值是多少 在 这些点附近, y=f(x) 的导数的符号有什么规律
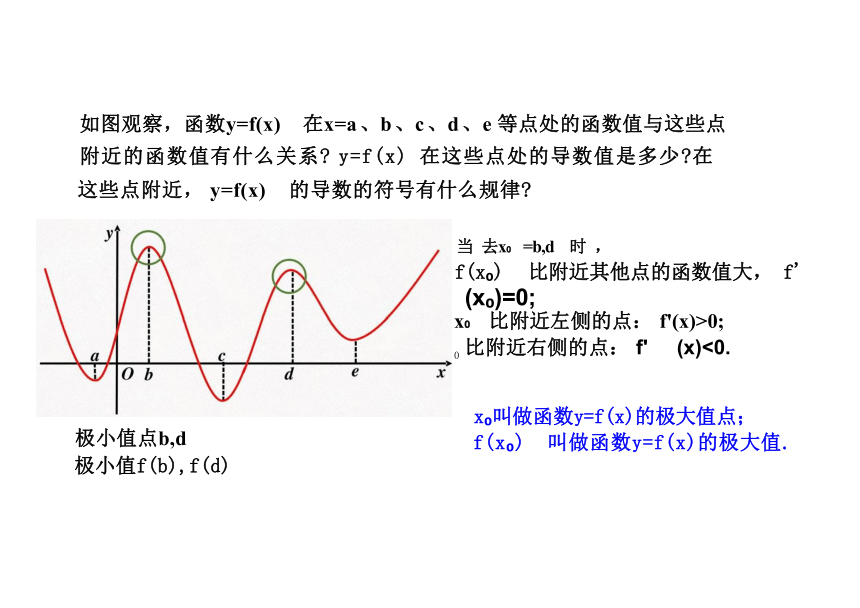
当 去x =b,d 时 ,
f(x ) 比附近其他点的函数值大, f' (x )=0;
x 比附近左侧的点: f'(x)>0;
0 比附近右侧的点: f' (x)<0.
x 叫做函数y=f(x)的极大值点;
f(x ) 叫做函数y=f(x)的极大值.
极小值点b,d
极小值f(b),f(d)
极值点 x 为极大值点
x 为极小值点
极值 f(x )为极大值
f(x )为极小值
条件 f'(x )=0 x 附近左侧f'(x )>0 x 附近右侧f'(x )<0
x 附近左侧f'(x )<0
x 附近右侧f'(x )>0
x 附近f(x)x 附近f(x)>f(x )
图像
注:
极大点,小值点统称极值点;极大/小值统称极值. 极值点左右两侧的导数值异号
极值反映了函数在某点附近的大小,刻画了函数的局部性 质.
问题1:一个函数的极大值或极小值是唯一的吗 不一定
如函数y=sinx 在R上有无数个极值。
问题2:任何一个函数一定有极大值或极小值吗 不一定
如函数y=x 在R上有无极值。
问题3:一个函数的极小值一定小于极大值吗 不一定
如函 极小值2大于极大值-
2
问题4:极值点可能是区间端点吗 不可能
问题5:若f'(x )=0, 则x 一定是极值点吗 不一定
如函数y=x 在满足f'(0)=0, 但x=0不是极值点。
结论: 若 f'(x )=0, 但 x 不一定是极值点。
结论:f′(x )=0 是可导函数在x 处取得极值的必要而不充分条件.
注:①若f'(x )=0, 且x 两侧导数异号,则x,是极值点。
②若x 是极值点,则f'(x )=0。
x, 是极值点是f'(x )=0 的充分不必要条件.
若f'(x)在 点x 的 左 右 两 侧 符 号 相 同 , 则fx ) 不 是 极 值 .
极大值和极小值的大小没有必然关系.
极值点必在区间内部, 区间端点不能作为极值点.
1( 课 本P92). 下图是导函数y=f(x)的图象,试找出函数y=f(x)的极值点,并指出哪些是
极大值点,哪些是极小值点.
解析:极值点有
X ,x . 其中极大值
点是x , 极小值点是
X4 ·
2.函数f(x) 的定义域为 (a,b), 其导函数f'(x) 在 (a,b) 内
的图像如图所示,则函数f(x)在 (a,b) 内 有 个极小值点。
例5(教材93)求函数f 的极值
求解函数极值的一般步骤:
(1)求函数的定义域;
(2)求函数的导函数f'(x);
(3)求方程f'(x)=0 的根;
(4)列表判断符号;
(5)求出极值。
左正右负极大值;
左负右正极小值.
练习:求函数f(x)=x -3x -9x+5 的极值。
f(x)的极大值为f(-1)=10,极小值为f(3)=-22.
课堂小结
本节课你学到了哪些知识
1.极小值、极大值的概念;
2.判断函数f(x) 极值的方法;
3.求可导函数f(x) 极值的步骤。
作业:P书92练习2(1),(2)题;
小书P147A.
选做题:1.求函数f(x)=x -x 的极值。
2.求函数f 的极值。
5.3.2 函数的极值与最大 (小)值(第一课时)
学习目标
1.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.
2.能利用导数求某些函数的极大值、极小值。
3.过理解函数的极值及其应用导数的求解过程,发展直观想象与数学运算素养。 教学重难点
教学重点:理解函数极小值点、极大值点和极大值、极小值。
教学难点:理解函数极小值点、极大值点和极大值、极小值概念。
复习回顾
函数单调性与导数的关系:
设函数y=f(x) 在区间(a,b) 内的导数为f'(x).
如果f'(x)>0, 则f(x)在(a,b)内为单调递增;
如果f'(x)<0,f(x) 在(a,b)内为单调递减;
如果f'(x)=0, 则f(x)在(a,b)内为常数函数;
反 之 ,
如果f(x)在(a,b)内为增函数,则f'(x)≥0 在(a,b)内恒成立;
如果f(x)在(a,b)内为减函数,则f'(x)≤0 在(a,b)内恒成立.
在用导数研究函数的单调性时,我们发现利用导数的正负可以 判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函 数有什么性质呢
这是江西庐山群山叠嶂的景象。
苏轼在《题西林壁》中这样写道:
“横看成岭侧成峰,远近高低各不
同”,描述的就是庐山的高低起伏, 错落有致。在群山之中,各个山峰的 顶端,虽然不是群山的最高处,但它 却是其附近的最高点。
在数学上,这种现象如何来刻画呢
即当t在a的附近从小到大经过a时 ,h'(t)先正后 负,且h'(t) 连续变化,于是有h'(a)=0.
(1) 对于一般的函数y=f(x), 是否也有同样的性质
观察下图,我们发现,当 t=a 时,高台跳水运动员距水面的高度最大.
函 数h(t) 在此点的导数是多少呢 此点附近的图象有什么特点 相应地, 导数的符号有什么变化规律
当tk
当t>a时,函数h(t)单调递减, h'(t)<0.
这就是说,在t=a 附近,函数值先增后减,
由图可以看出,h'(a)=0;
在t=a的附近,
放大t=a附近的图象,如图0(2)所示.
单调性递减,
这些点附近,y=f(x) 的导数的符号有什么规律
当去x =a,c,e 时,
f(x ) 比附近其他点的函数值小,f' (x )=0;
x 比附近左侧的点:f' (x)<0;
0比附近右侧的点:f'(x)>0.
x 叫做函数y=f(x)的极小值点;
f(x ) 叫做函数y=f(x)的极小值.
极小值点a,c,e
极小值f(a),f(c),f(e)
如图观察,函数y=f(x) 在x=a、b、c、d、e等点处的函数值与这些点
附近的函数值有什么关系 y=f(x) 在这些点处的导数值是多少 在
如图观察,函数y=f(x) 在x=a 、b 、c 、d 、e 等点处的函数值与这些点
附近的函数值有什么关系 y=f(x) 在这些点处的导数值是多少 在 这些点附近, y=f(x) 的导数的符号有什么规律
当 去x =b,d 时 ,
f(x ) 比附近其他点的函数值大, f' (x )=0;
x 比附近左侧的点: f'(x)>0;
0 比附近右侧的点: f' (x)<0.
x 叫做函数y=f(x)的极大值点;
f(x ) 叫做函数y=f(x)的极大值.
极小值点b,d
极小值f(b),f(d)
极值点 x 为极大值点
x 为极小值点
极值 f(x )为极大值
f(x )为极小值
条件 f'(x )=0 x 附近左侧f'(x )>0 x 附近右侧f'(x )<0
x 附近左侧f'(x )<0
x 附近右侧f'(x )>0
x 附近f(x)
图像
注:
极大点,小值点统称极值点;极大/小值统称极值. 极值点左右两侧的导数值异号
极值反映了函数在某点附近的大小,刻画了函数的局部性 质.
问题1:一个函数的极大值或极小值是唯一的吗 不一定
如函数y=sinx 在R上有无数个极值。
问题2:任何一个函数一定有极大值或极小值吗 不一定
如函数y=x 在R上有无极值。
问题3:一个函数的极小值一定小于极大值吗 不一定
如函 极小值2大于极大值-
2
问题4:极值点可能是区间端点吗 不可能
问题5:若f'(x )=0, 则x 一定是极值点吗 不一定
如函数y=x 在满足f'(0)=0, 但x=0不是极值点。
结论: 若 f'(x )=0, 但 x 不一定是极值点。
结论:f′(x )=0 是可导函数在x 处取得极值的必要而不充分条件.
注:①若f'(x )=0, 且x 两侧导数异号,则x,是极值点。
②若x 是极值点,则f'(x )=0。
x, 是极值点是f'(x )=0 的充分不必要条件.
若f'(x)在 点x 的 左 右 两 侧 符 号 相 同 , 则fx ) 不 是 极 值 .
极大值和极小值的大小没有必然关系.
极值点必在区间内部, 区间端点不能作为极值点.
1( 课 本P92). 下图是导函数y=f(x)的图象,试找出函数y=f(x)的极值点,并指出哪些是
极大值点,哪些是极小值点.
解析:极值点有
X ,x . 其中极大值
点是x , 极小值点是
X4 ·
2.函数f(x) 的定义域为 (a,b), 其导函数f'(x) 在 (a,b) 内
的图像如图所示,则函数f(x)在 (a,b) 内 有 个极小值点。
例5(教材93)求函数f 的极值
求解函数极值的一般步骤:
(1)求函数的定义域;
(2)求函数的导函数f'(x);
(3)求方程f'(x)=0 的根;
(4)列表判断符号;
(5)求出极值。
左正右负极大值;
左负右正极小值.
练习:求函数f(x)=x -3x -9x+5 的极值。
f(x)的极大值为f(-1)=10,极小值为f(3)=-22.
课堂小结
本节课你学到了哪些知识
1.极小值、极大值的概念;
2.判断函数f(x) 极值的方法;
3.求可导函数f(x) 极值的步骤。
作业:P书92练习2(1),(2)题;
小书P147A.
选做题:1.求函数f(x)=x -x 的极值。
2.求函数f 的极值。
