6.2.4 组合数 课件(共22张PPT)-高二下学期数学人教A版选择性必修第三册
文档属性
| 名称 | 6.2.4 组合数 课件(共22张PPT)-高二下学期数学人教A版选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
第六单元
6.2.4 组合数
预 习
预习课本P23— —P25的内容
② 学习目标
1: 理解组合数的概念,掌握组合数公式及其推导过程。 能正确区分排列与组合,灵活运用组合数公式解决实际问 题(如分组、抽样问题)。
2: 通过对比排列与组合的联系与区别,体会从具体到抽象 的数学思维,通过组合数性质的探究,培养逻辑推理能力。
3: 感受组合数在概率统计、计算机科学等领域的应用价值。
学习重难点
重点:组合数公式的推导与应用。
难点:组合与排列的区分;实际问题中组合模
型的构建。
4 复 习 导 入
1.排列的定义是什么 如何计算A
2:排列的关键点:元素互异、顺序影响结果(举例:ab与ba不同)
3: 排列数公式一:A"=n(m-1)(n-2) … … -m+1)
4: 排列数公式二:
⑤ 概念引入
上节课我们已经学习过组合,类比排列数,那么组合
数的概念
“一般地, 从n 个不同元素中取出m(m≤n) 个元素的所有不同
组合的个数, 叫 做从n 个不同元素中取出m 个元素的组合数,用
符号Cm 表示。
符号C" C 是英文combination (组合)的第 一个字母,组合数还可以用 n
符号(
组合数定义:
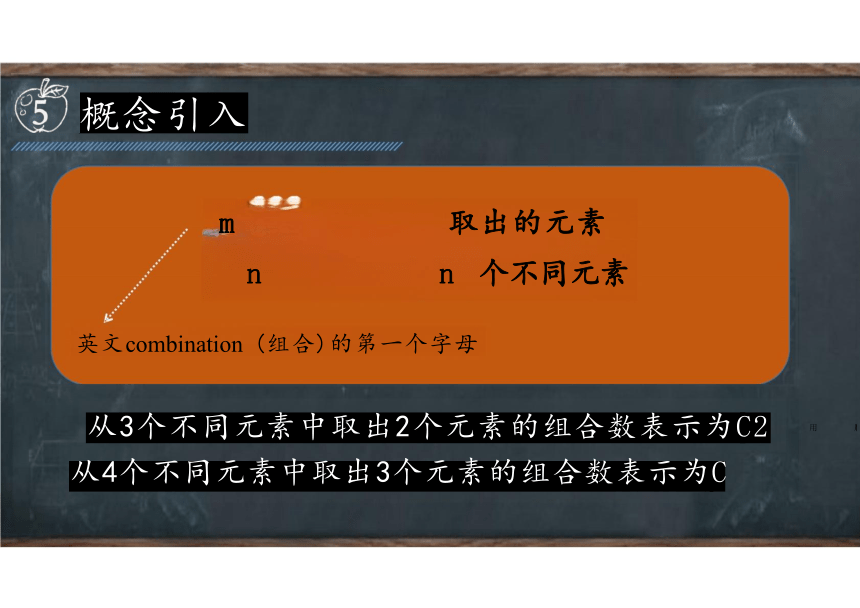
概念引入
m 取出的元素 n n 个不同元素 英文combination (组合)的第一个字母 从3个不同元素中取出2个元素的组合数表示为C2 从4个不同元素中取出3个元素的组合数表示为C
用雕丽王强周五
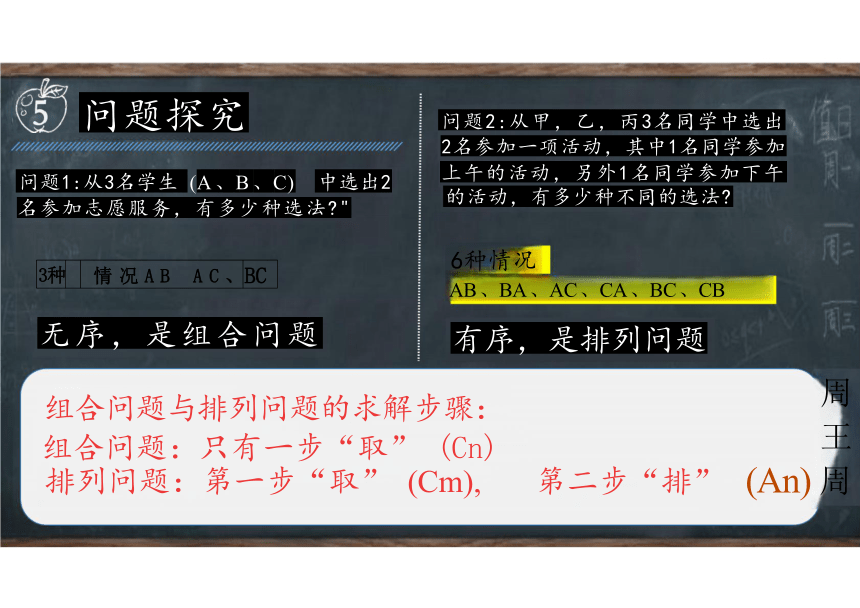
组合问题与排列问题的求解步骤:
组合问题:只有一步“取” (Cn)
排列问题:第一步“取” (Cm), 第二步“排”
问题探究
问题1:从3名学生 (A 、B 、C) 中选出2 名参加志愿服务,有多少种选法 "
6种情况
AB 、BA 、AC 、CA 、BC 、CB
有序,是排列问题
问题2:从甲,乙,丙3名同学中选出 2名参加一项活动,其中1名同学参加
上午的活动,另外1名同学参加下午 的活动,有多少种不同的选法
无序,是组合问题
3种 情 况 A B A C 、
BC
(An) 周
周 王
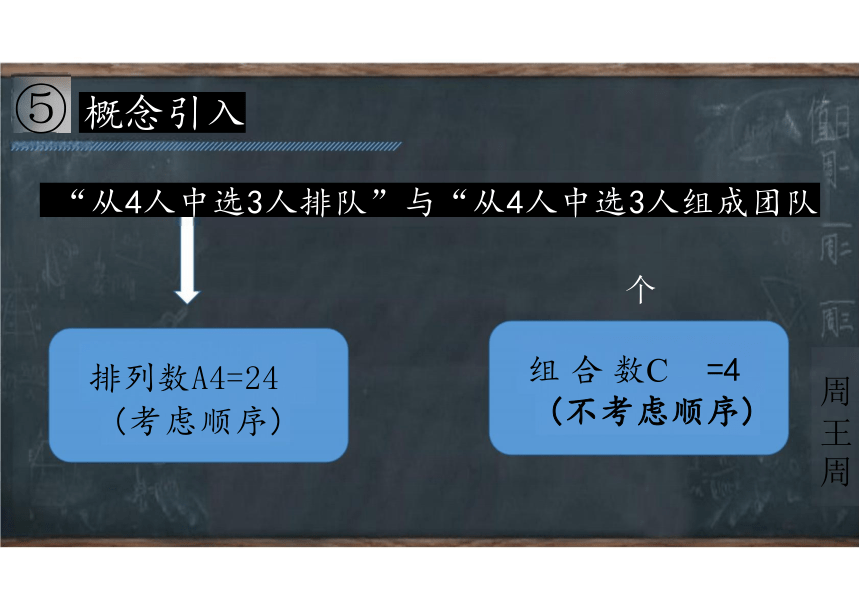
⑤ 概念引入
“从4人中选3人排队”与“从4人中选3人组成团队
个
组 合 数C =4
(不考虑顺序)
排列数A4=24
(考虑顺序)
周王周
公式推导
问题2:从4个不同的元素中取出3个元素进行排列
abc ,bac,cab,acb,bca,cb
a,abd,bad,dab,abd,bda,
排列 dba,acd,cad,dac,adc,cda ,dca,bsd,cbd,bdc,dbc,cd b,dcb
A = C4A
c-
第一步:从4个元素中取出三个元素作为 一 组,共有C 种不同
第二步:将取出的3个元素作为金排列,共有A 种不同的排法。
a,b,c
a,b,d a,c,d b,c,d
值 周
的取法 。
组合
公式推导
问题2:从m 个不同的元素中取出m 个元素进行排列
第一步:从n个元素中取出m 个元素作为一组,共有Cm种不同的取法。
第二步:将取出的m个元素作为全排列,共有种A黑不同的排法。
An=CmAm
这里n,m ∈N*, 并且m≤n, 这个公式叫做组合数公式
n l
当An=( n-m)! —→
规定CO=1 Ch=1 Cn=n
公式推导
组合数公式:
值 周
组合数性质
性质1: (称对性)
验 证 :
性质2: (递推关系)
验 证 :
公式性质
几何解释:杨辉三角的生成规律。
常用组合数恒等式
(1)
(2)Cm=”Cm-1
(5)CmCn+Cn Ch+…….CmCh=Cm+n
公式性质
(2) C10 (3)C18 (4)C10
例6计算
(1)Ci0
课堂练习
例7在100件产品中,有98件合格品,2件次品,从100件产品中任意抽 出3件
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
课堂练习
例8(易错题):从5男3女中选3人,要求至少有1名女生,有
课堂练习
多少种选法
1.计 算
(1)C -c 哈
随堂练习
1)3C -2C
2. 某班有30人,需选派5人参加活动,甲乙至少1人参加,有
随堂练习
多少种选法
3.性 质及应用场景。
归纳小结
1.组合数的定义、
2.公式、
小 结 :
作业布置
基础题:教材P25 习题6.2第1、3题。
-探究题:证明组合数性质
周
五
每次归程
都是为了更好出发
每次停歇
都是为了积攒力量
第六单元
6.2.4 组合数
预 习
预习课本P23— —P25的内容
② 学习目标
1: 理解组合数的概念,掌握组合数公式及其推导过程。 能正确区分排列与组合,灵活运用组合数公式解决实际问 题(如分组、抽样问题)。
2: 通过对比排列与组合的联系与区别,体会从具体到抽象 的数学思维,通过组合数性质的探究,培养逻辑推理能力。
3: 感受组合数在概率统计、计算机科学等领域的应用价值。
学习重难点
重点:组合数公式的推导与应用。
难点:组合与排列的区分;实际问题中组合模
型的构建。
4 复 习 导 入
1.排列的定义是什么 如何计算A
2:排列的关键点:元素互异、顺序影响结果(举例:ab与ba不同)
3: 排列数公式一:A"=n(m-1)(n-2) … … -m+1)
4: 排列数公式二:
⑤ 概念引入
上节课我们已经学习过组合,类比排列数,那么组合
数的概念
“一般地, 从n 个不同元素中取出m(m≤n) 个元素的所有不同
组合的个数, 叫 做从n 个不同元素中取出m 个元素的组合数,用
符号Cm 表示。
符号C" C 是英文combination (组合)的第 一个字母,组合数还可以用 n
符号(
组合数定义:
概念引入
m 取出的元素 n n 个不同元素 英文combination (组合)的第一个字母 从3个不同元素中取出2个元素的组合数表示为C2 从4个不同元素中取出3个元素的组合数表示为C
用雕丽王强周五
组合问题与排列问题的求解步骤:
组合问题:只有一步“取” (Cn)
排列问题:第一步“取” (Cm), 第二步“排”
问题探究
问题1:从3名学生 (A 、B 、C) 中选出2 名参加志愿服务,有多少种选法 "
6种情况
AB 、BA 、AC 、CA 、BC 、CB
有序,是排列问题
问题2:从甲,乙,丙3名同学中选出 2名参加一项活动,其中1名同学参加
上午的活动,另外1名同学参加下午 的活动,有多少种不同的选法
无序,是组合问题
3种 情 况 A B A C 、
BC
(An) 周
周 王
⑤ 概念引入
“从4人中选3人排队”与“从4人中选3人组成团队
个
组 合 数C =4
(不考虑顺序)
排列数A4=24
(考虑顺序)
周王周
公式推导
问题2:从4个不同的元素中取出3个元素进行排列
abc ,bac,cab,acb,bca,cb
a,abd,bad,dab,abd,bda,
排列 dba,acd,cad,dac,adc,cda ,dca,bsd,cbd,bdc,dbc,cd b,dcb
A = C4A
c-
第一步:从4个元素中取出三个元素作为 一 组,共有C 种不同
第二步:将取出的3个元素作为金排列,共有A 种不同的排法。
a,b,c
a,b,d a,c,d b,c,d
值 周
的取法 。
组合
公式推导
问题2:从m 个不同的元素中取出m 个元素进行排列
第一步:从n个元素中取出m 个元素作为一组,共有Cm种不同的取法。
第二步:将取出的m个元素作为全排列,共有种A黑不同的排法。
An=CmAm
这里n,m ∈N*, 并且m≤n, 这个公式叫做组合数公式
n l
当An=( n-m)! —→
规定CO=1 Ch=1 Cn=n
公式推导
组合数公式:
值 周
组合数性质
性质1: (称对性)
验 证 :
性质2: (递推关系)
验 证 :
公式性质
几何解释:杨辉三角的生成规律。
常用组合数恒等式
(1)
(2)Cm=”Cm-1
(5)CmCn+Cn Ch+…….CmCh=Cm+n
公式性质
(2) C10 (3)C18 (4)C10
例6计算
(1)Ci0
课堂练习
例7在100件产品中,有98件合格品,2件次品,从100件产品中任意抽 出3件
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
课堂练习
例8(易错题):从5男3女中选3人,要求至少有1名女生,有
课堂练习
多少种选法
1.计 算
(1)C -c 哈
随堂练习
1)3C -2C
2. 某班有30人,需选派5人参加活动,甲乙至少1人参加,有
随堂练习
多少种选法
3.性 质及应用场景。
归纳小结
1.组合数的定义、
2.公式、
小 结 :
作业布置
基础题:教材P25 习题6.2第1、3题。
-探究题:证明组合数性质
周
五
每次归程
都是为了更好出发
每次停歇
都是为了积攒力量
