北师大版(2024)七年级数学下册 1.1 第5课时 零指数幂和负指数幂 课件(共15张PPT)
文档属性
| 名称 | 北师大版(2024)七年级数学下册 1.1 第5课时 零指数幂和负指数幂 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 38.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-20 20:03:05 | ||
图片预览






文档简介
(共15张PPT)
第一章 整式的乘除
1 幂的乘除
第5课时 零指数幂和负指数幂
幂的意义:
a·a· … ·a
n个a
=
同底幂的除法运算法则:
同底数幂的乘法运算法则:
第5课时
零指数幂和负指数幂
讨论下列问题:(1)同底数幂相除法则中各字母必须满足什么条件?
(a≠0,m,n都是正整数,且m>n)
同底数幂相除,底数_____,指数______.
不变
相减
(2)要使 也能成立,你认为应当规定 等于多少?
(3)要使 和 也成立,应当规定 和 分别等于多少呢?
第5课时
零指数幂和负指数幂
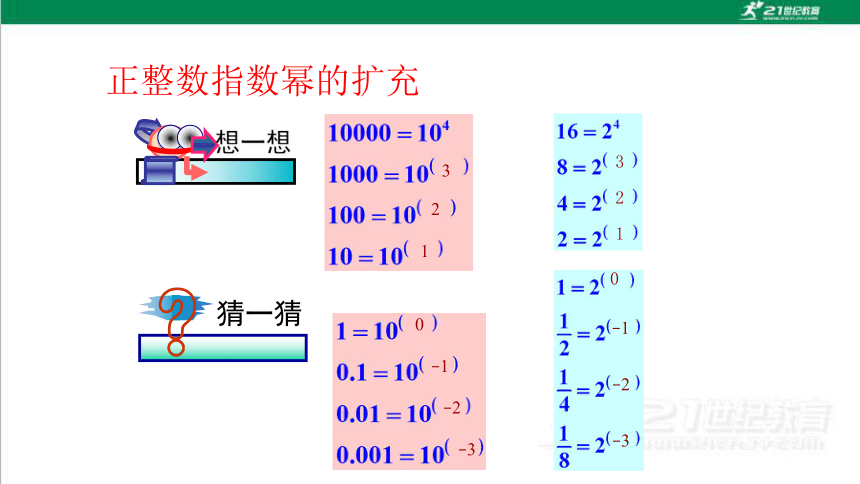
正整数指数幂的扩充
想一想
3
2
1
猜一猜
?
0
–1
–2
–3
3
2
1
0
–1
–2
–3
规定: a = 1 , (a≠0)
0
(a≠0 ,p是正整数)
任何不等于零的数,它的零次幂等于1.
任何不等于零的数的 -p ( p 是正整数)次幂,等于这个数的 p 次幂的倒数.
零指数幂、负指数幂的理解
为使“同底数幂的运算法则am÷an=am–n通行无阻:
所以规定 a0 =1;
am÷am=am–m
(a≠0, m,n都是正整数)
=
a0,
1=
当p是正整数时,
=a0÷ap
=a0-p
=a-p
所以规定 :
某种细胞分裂时,1个细胞分裂1次变为2个,分裂2次变为4个,分裂3次变为8个……
你能由此说明20=1的合理性吗?
例1 用小数或分数表示下列各数:
(1) ; (2) ; (3)
(1)
(2)
(3)
解:
计算下列各式,你有什么发现?与同伴交流.
发现:引入零指数幂和负整数指数幂后,正整数指数幂的运算性质在指数是整数时仍然适用.
例2 计算:
解:
例3 计算:
①x12÷x-4 ②(-y)3÷(-y)-2
③-(k6÷k-6) ④(-y)-5÷y4
⑤m÷m0 ⑥(mn)5÷(mn)6
原式=x16
原式=-y5
原式=-k12
原式=-y-9
原式=m
原式=(mn)-1
1.计算:
2.计算:
① (x-1)2·x-2÷x0 ②-2-1×20250-(-1)-8
=x-2 ·x-2÷x0
=x-4
规定 :
第5课时
零指数幂和负指数幂
第一章 整式的乘除
1 幂的乘除
第5课时 零指数幂和负指数幂
幂的意义:
a·a· … ·a
n个a
=
同底幂的除法运算法则:
同底数幂的乘法运算法则:
第5课时
零指数幂和负指数幂
讨论下列问题:(1)同底数幂相除法则中各字母必须满足什么条件?
(a≠0,m,n都是正整数,且m>n)
同底数幂相除,底数_____,指数______.
不变
相减
(2)要使 也能成立,你认为应当规定 等于多少?
(3)要使 和 也成立,应当规定 和 分别等于多少呢?
第5课时
零指数幂和负指数幂
正整数指数幂的扩充
想一想
3
2
1
猜一猜
?
0
–1
–2
–3
3
2
1
0
–1
–2
–3
规定: a = 1 , (a≠0)
0
(a≠0 ,p是正整数)
任何不等于零的数,它的零次幂等于1.
任何不等于零的数的 -p ( p 是正整数)次幂,等于这个数的 p 次幂的倒数.
零指数幂、负指数幂的理解
为使“同底数幂的运算法则am÷an=am–n通行无阻:
所以规定 a0 =1;
am÷am=am–m
(a≠0, m,n都是正整数)
=
a0,
1=
当p是正整数时,
=a0÷ap
=a0-p
=a-p
所以规定 :
某种细胞分裂时,1个细胞分裂1次变为2个,分裂2次变为4个,分裂3次变为8个……
你能由此说明20=1的合理性吗?
例1 用小数或分数表示下列各数:
(1) ; (2) ; (3)
(1)
(2)
(3)
解:
计算下列各式,你有什么发现?与同伴交流.
发现:引入零指数幂和负整数指数幂后,正整数指数幂的运算性质在指数是整数时仍然适用.
例2 计算:
解:
例3 计算:
①x12÷x-4 ②(-y)3÷(-y)-2
③-(k6÷k-6) ④(-y)-5÷y4
⑤m÷m0 ⑥(mn)5÷(mn)6
原式=x16
原式=-y5
原式=-k12
原式=-y-9
原式=m
原式=(mn)-1
1.计算:
2.计算:
① (x-1)2·x-2÷x0 ②-2-1×20250-(-1)-8
=x-2 ·x-2÷x0
=x-4
规定 :
第5课时
零指数幂和负指数幂
同课章节目录
