4.3.2等比数列的前n项和公式(第1课时) 课件(共19张PPT)-高二上学期数学人教A版选择性必修第二册
文档属性
| 名称 | 4.3.2等比数列的前n项和公式(第1课时) 课件(共19张PPT)-高二上学期数学人教A版选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:15:37 | ||
图片预览





文档简介
(共19张PPT)
4.3.2等比数列的前n 项和公式
(第1课时)
第四章 数列
相传古印度的舍罕王打算重赏国际象棋的发明者——
宰相西萨 ·班 ·达依尔,于是,这位国王对宰相说:
问题引入
情境 一
177
数学小故事
:说吧,想要什么赏赐
陛下,请您在这张棋盘的第1个小格内,赏给我1
粒麦子;在第二个小格内给2粒;第三格内给4粒, 照这样下去,每1小格都是前1小格的2倍.
:就只这点要求吗 就算摆满棋盘应该也用不了多少小麦.
陛下啊,就这样摆满棋盘上所有64格,把所有这
些麦粒赏给我吧!
:好吧,来人从仓库里运出给宰相的小麦.
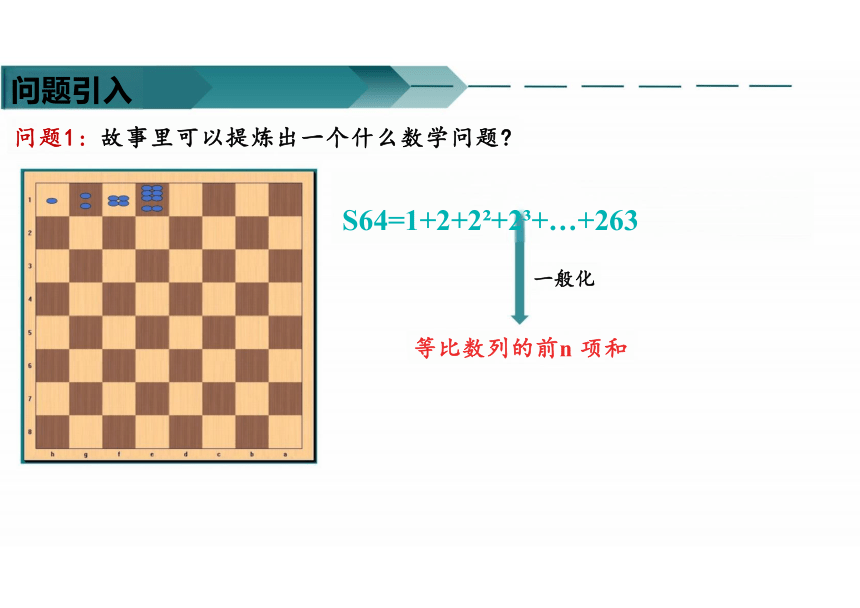
S64=1+2+2 +2 +…+263
一般化
等比数列的前n 项和
问题1: 故事里可以提炼出一个什么数学问题
问题引入
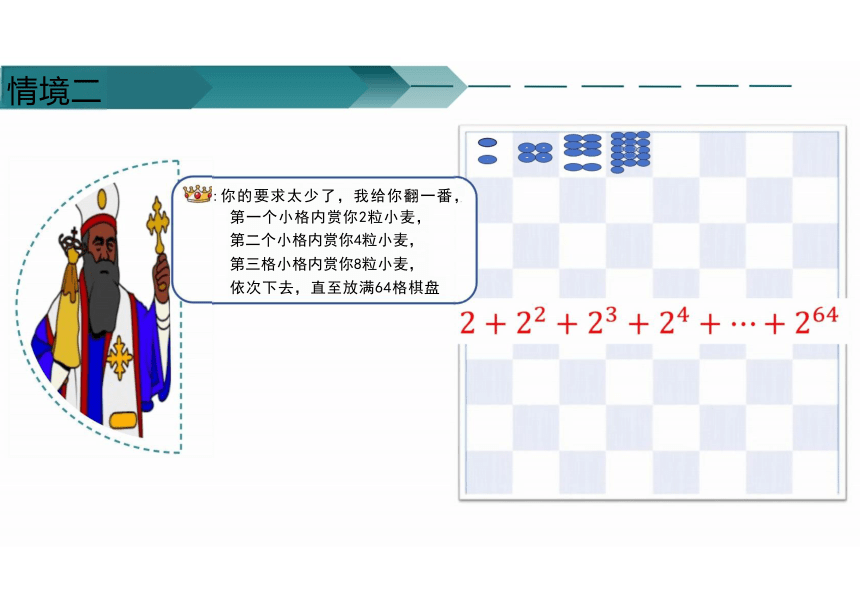
:你的要求太少了,我给你翻一番, 第一个小格内赏你2粒小麦,
第二个小格内赏你4粒小麦,
第三格小格内赏你8粒小麦,
依次下去,直至放满64格棋盘
情境二
探究:更一般地,首项为a , 公比为q的等比数列如何求和
Sn=a1+a2+a3+…+an
Sn=a +a q+a q +…+a qn-1=
问题2:如何推导证明等比数列的前n 项和公式呢
理解公式推导的过程:
任务1:请同学们试着自主独立完成等比数列前n 项和公式的推导.
结合教材第34页至第35页“如何求一个等比数列前n 项和”相关内容.
新知探究
证明:错位相减法
Sn=a + a 1q+a q +a q + … +a qn -1
qSn=a q + a q +a q +…+a qn-1+a qn
两式作差得: Sn-qSn=a -a qn
☆证明等比数列求和公式 ,q≠1
新知探究
欧拉(Euler)
所以
任务2:请同学们小组合作探究:除了乘以q, 还可以乘以其它数吗
新 知 探 究
同乘
作 差 消 项
向前错位
向前错位
同乘 q :Sn=a +a1q+a1q +…+a1qn-2+a1qn-1 作 差 消 项
向后错 q Sn=a1q +a1qβ+…+a1qn-1+a1qn+a1qn+1
两位
任务2:请同学们小组合作探究:除了乘以q, 还可以乘以其它数吗
新知探究
归纳总结
☆等比数列求和公式 注 意:使用公式前,先判断公比q 是否为1
,(q≠ 1) 已知a ,q,n, 则
末项
项数
公比
首 项
前 n 项 和
已 知a ,q,an,
则
特殊情况:当q=1 时 ,Sn=na .
知三求二
指数爆炸式增长的“威力”!
国王做不到
回归情境
问题3: 回归故事情境,宰相到底要多少粒麦粒
1+2+2 +2 +…+263
1000粒麦子的质量约为40g 发明者要求的麦粒的总质量超过了7000亿吨
是2023~2024年世界小麦年产量(7亿多吨)的981倍,按每年7亿吨计算
Sn=ai+ail+aZ +..+agn-I
二 a1+9(ai+a12+- 十 ai2n-2)
=a1+2Sn-1(n≥2).
∵Sn-1=Sn-an .
六 Sn= ar+9CSn-an)
即(1-2)Sn=ar-2an
问题4: 你还有没有其它方法来证明等比数列的前n项和公式
提取/公因式法:
古埃及
新知探究
(L≠1)
新知探究
问题4: 你还有没有其它方法来证明等比数列的前n 项和公式
∵a,+astayt…tun=Sn-a
由等比数列得 a,ta2+a3+ ..an1-an
n-a=qsn-an
(1-a)S=,-a
S:
==
由等比定理得
a=
欧几里德(Euclid)
问题4: 你还有没有其它方法来证明等比数列的前n项和公式
李作
Sn=a1+qSn
拉克洛瓦(Lacroix)
新知探究
例1: 我国明代数学家程大位所著的《算法统宗》记载:
远 望 巍 巍 塔 七 层 , 红 光 点 点 倍 加 增 ,
共 灯 三 百 八 十 一 , 请 问 尖 头 几 盏 灯
翻译:已知等比数列{an}中,
n=7,q=2,S =381, 求a .
解:由等比数列的前n项和公式
解得: a =3
(3)若a =8, ,求n.
(2)由已知可得2' (3)由等比数列的前n项和公式,可得
变式1-1:
(1)若 9 ,求Sg; 解:(1)
(2)若a =27, ,q<0, 求!
练 习 巩 固
解得
解得n=5.
Tn=b +b +b +…+bn-2+bn-1+bn 结合等差数列的性质
Sn=a1+a +a +…+an-2+an -1+an 结合等比数列的定义
等差数列求和 高斯用首尾相加法来“消项”
倒序相加法
等比数列求和 欧拉用错位相减法来“消项”
错位相减法
一个承诺,
国王没有做到;
一个问题,
数学家们没有止步 .
我相信,
你会像数学家们 一样,
站在巨人的肩膀上 .
当你用好发现美的第三只眼睛——数学,
你会做得更好!
今日作业
1 、大 册P26探究一和探究二
2、作业本作业:
课本P37练习1、3、4、5.
4.3.2等比数列的前n 项和公式
(第1课时)
第四章 数列
相传古印度的舍罕王打算重赏国际象棋的发明者——
宰相西萨 ·班 ·达依尔,于是,这位国王对宰相说:
问题引入
情境 一
177
数学小故事
:说吧,想要什么赏赐
陛下,请您在这张棋盘的第1个小格内,赏给我1
粒麦子;在第二个小格内给2粒;第三格内给4粒, 照这样下去,每1小格都是前1小格的2倍.
:就只这点要求吗 就算摆满棋盘应该也用不了多少小麦.
陛下啊,就这样摆满棋盘上所有64格,把所有这
些麦粒赏给我吧!
:好吧,来人从仓库里运出给宰相的小麦.
S64=1+2+2 +2 +…+263
一般化
等比数列的前n 项和
问题1: 故事里可以提炼出一个什么数学问题
问题引入
:你的要求太少了,我给你翻一番, 第一个小格内赏你2粒小麦,
第二个小格内赏你4粒小麦,
第三格小格内赏你8粒小麦,
依次下去,直至放满64格棋盘
情境二
探究:更一般地,首项为a , 公比为q的等比数列如何求和
Sn=a1+a2+a3+…+an
Sn=a +a q+a q +…+a qn-1=
问题2:如何推导证明等比数列的前n 项和公式呢
理解公式推导的过程:
任务1:请同学们试着自主独立完成等比数列前n 项和公式的推导.
结合教材第34页至第35页“如何求一个等比数列前n 项和”相关内容.
新知探究
证明:错位相减法
Sn=a + a 1q+a q +a q + … +a qn -1
qSn=a q + a q +a q +…+a qn-1+a qn
两式作差得: Sn-qSn=a -a qn
☆证明等比数列求和公式 ,q≠1
新知探究
欧拉(Euler)
所以
任务2:请同学们小组合作探究:除了乘以q, 还可以乘以其它数吗
新 知 探 究
同乘
作 差 消 项
向前错位
向前错位
同乘 q :Sn=a +a1q+a1q +…+a1qn-2+a1qn-1 作 差 消 项
向后错 q Sn=a1q +a1qβ+…+a1qn-1+a1qn+a1qn+1
两位
任务2:请同学们小组合作探究:除了乘以q, 还可以乘以其它数吗
新知探究
归纳总结
☆等比数列求和公式 注 意:使用公式前,先判断公比q 是否为1
,(q≠ 1) 已知a ,q,n, 则
末项
项数
公比
首 项
前 n 项 和
已 知a ,q,an,
则
特殊情况:当q=1 时 ,Sn=na .
知三求二
指数爆炸式增长的“威力”!
国王做不到
回归情境
问题3: 回归故事情境,宰相到底要多少粒麦粒
1+2+2 +2 +…+263
1000粒麦子的质量约为40g 发明者要求的麦粒的总质量超过了7000亿吨
是2023~2024年世界小麦年产量(7亿多吨)的981倍,按每年7亿吨计算
Sn=ai+ail+aZ +..+agn-I
二 a1+9(ai+a12+- 十 ai2n-2)
=a1+2Sn-1(n≥2).
∵Sn-1=Sn-an .
六 Sn= ar+9CSn-an)
即(1-2)Sn=ar-2an
问题4: 你还有没有其它方法来证明等比数列的前n项和公式
提取/公因式法:
古埃及
新知探究
(L≠1)
新知探究
问题4: 你还有没有其它方法来证明等比数列的前n 项和公式
∵a,+astayt…tun=Sn-a
由等比数列得 a,ta2+a3+ ..an1-an
n-a=qsn-an
(1-a)S=,-a
S:
==
由等比定理得
a=
欧几里德(Euclid)
问题4: 你还有没有其它方法来证明等比数列的前n项和公式
李作
Sn=a1+qSn
拉克洛瓦(Lacroix)
新知探究
例1: 我国明代数学家程大位所著的《算法统宗》记载:
远 望 巍 巍 塔 七 层 , 红 光 点 点 倍 加 增 ,
共 灯 三 百 八 十 一 , 请 问 尖 头 几 盏 灯
翻译:已知等比数列{an}中,
n=7,q=2,S =381, 求a .
解:由等比数列的前n项和公式
解得: a =3
(3)若a =8, ,求n.
(2)由已知可得2' (3)由等比数列的前n项和公式,可得
变式1-1:
(1)若 9 ,求Sg; 解:(1)
(2)若a =27, ,q<0, 求!
练 习 巩 固
解得
解得n=5.
Tn=b +b +b +…+bn-2+bn-1+bn 结合等差数列的性质
Sn=a1+a +a +…+an-2+an -1+an 结合等比数列的定义
等差数列求和 高斯用首尾相加法来“消项”
倒序相加法
等比数列求和 欧拉用错位相减法来“消项”
错位相减法
一个承诺,
国王没有做到;
一个问题,
数学家们没有止步 .
我相信,
你会像数学家们 一样,
站在巨人的肩膀上 .
当你用好发现美的第三只眼睛——数学,
你会做得更好!
今日作业
1 、大 册P26探究一和探究二
2、作业本作业:
课本P37练习1、3、4、5.
