〖数学〗平面与平面垂直 课件(共26张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 〖数学〗平面与平面垂直 课件(共26张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:22:18 | ||
图片预览






文档简介
(共26张PPT)
普通高中数学 人教版(2019)必修第二册
第八章立体几何初步
8.6.3平面与平面垂直
情景引入
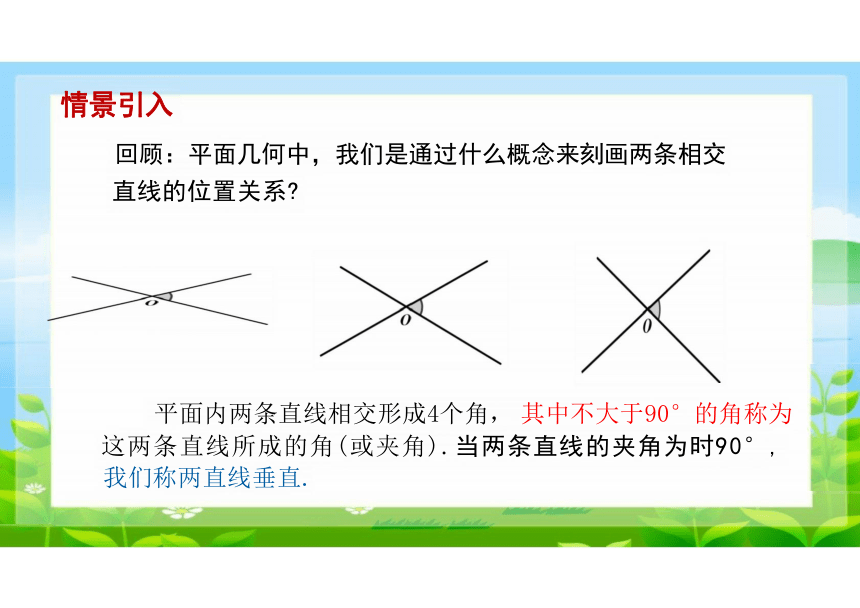
回顾:平面几何中,我们是通过什么概念来刻画两条相交
直线的位置关系
平面内两条直线相交形成4个角, 其中不大于90°的角称为
这两条直线所成的角(或夹角).当两条直线的夹角为时90°,
我们称两直线垂直.
情景引入
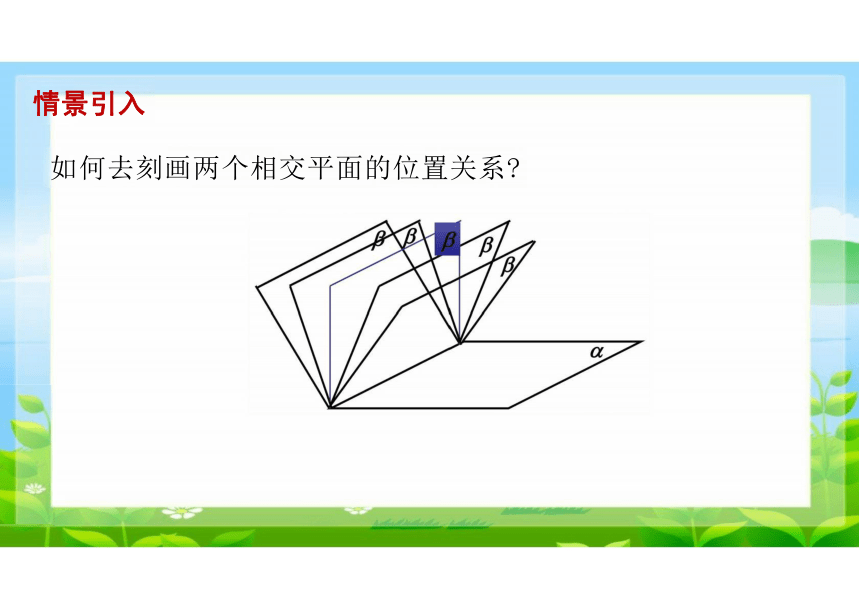
如何去刻画两个相交平面的位置关系
探究新知——二面角
类比直线间的夹角,引入二面角的概念:
如图,从一条直线出发的两个半平面所组成的图形叫做二面角.
这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
半平面 半平面
直线将平面分成两
部分,每一部分叫
半平面 .
平面角由射线--点--射线构成 二面角由半平面--棱--半平面构成。
记作:
记作:∠AOB AB-
P Q
-
P
-A
0
-
二面角的记法:
. Q B
l .P 印
C
A
探究新知
角的记法:
o<
二面角
A
B
探究新知——二面角
你能举出生活中常见的二面角吗
O
如何去度量二面角大小
O
观察探究
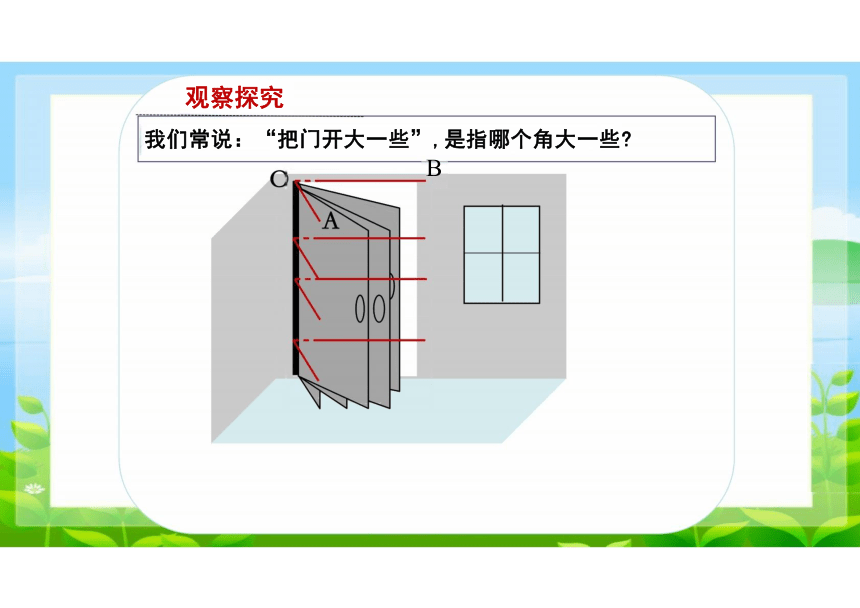
我们常说:“把门开大一些”,是指哪个角大一些
B
探究新知——二面角的平面角
二面角的平面角的定义
在二面角α-l-β 的棱上任取一
点O,以点O 为垂足,在半平面α和β内
分别作垂直于棱l 的射线OA和OB, 则
射线OA和OB构成的∠AOB叫做二面
角的平面角. 0 ∈l 空间角平面化
OA⊥1
OB⊥1=∠AOB 为二面角α-I- 的平面角
OBcp
符号语言
在棱上选多个点,画出多个所折二面角
的一个平面角,这些角相等吗
你能用某个定理解释为什么
这些角都是相等的吗
A
课后实验:同学们可以自己动手画 出若干个折纸所形成二面角的平面 角,比较它们的大小.
探究新知——二面角的平面角
B C
D
Q
P
二面角的大小可以用其平面角来度量,
二面角的平面角是多少度,
就说这个二面角是多少度.
探究新知——二面角的平面角
想一想:二面角平面角的取值范围是
[0,π]
10
平面角是直角的二面角叫做直二面角.
探究新知——直二面角
探究新知——面面垂直定义
两平面垂直的定义:
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这
如下图,画两个互相垂直的平面时,通常把表示平面的两个平行
两个平面互相垂直.平面α与β垂直,记作α⊥β.
四边形的一组边画成垂直.
探究新知——面面垂直判定定理
实例1 发现:线面垂直,则面面垂直
建筑工人砌墙时,如何
使所砌的墙和水平面垂
直
探索定理
实例2
一扇门在打开的过程中,门所在平 面和水平地面是否始终垂直
你能根据这些实例归纳总结出判定
面面垂直所需的条件吗
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
符号表示: aLβ,aca=aLβ
探究新知——面面垂直判定定理
简记:线面垂直,则面面垂直
探究新知—— 面面垂直判定定理
A
想一想 :
怎么证明面面垂直 的判定定理
C
β
α
B
文字语言 图形语言
符号语言
一个平面过 另一个平面的 垂线,则这两 个平面垂直.
c=aL
探究新知—— 面面垂直判定定理
平面与平面垂直的判定定理
例题讲解——新知应用
例7 如图,在正方体ABCD-A'B'C'D 中,求证平面A'BD⊥ 平面ACC'A'.
例题讲解——新知应用
例7 如图,在正方体ABCD-A'B'C'D 中,求证平面A'BD⊥ 平 面ACC'A'.
证明:∵ABCD-A'B'C'D '是正方体,
∴AA'⊥ 平面ABCD
∴AA'⊥BD,
又BDIAC, 且AA'∩AC=A,
∴BD⊥ 平 面ACC'A',
又BDc 平面A'BD,
∴平面A'BD⊥平面ACC'A'.
C
例题讲解——新知应用
例8 如图,AB 是圆O 的直径,PA 垂直于⊙O 所在的平面,
B
A ∈ 0
本质:线⊥面 面⊥面
关键:在一个平面内找另一个平面的垂线
图中还有哪些平
面是互相垂直的
呢
o 面PAC⊥ 面ABC 面PAB⊥ 面ABC
C是圆周上不同于A,B 的任意一点,
求证:平面PAC⊥平 面PBC. P
BC⊥ 面PAC
业
平面PAC⊥平面PBC
业
BC⊥AC BCLPA
PA⊥面ABC
BCc 面ABC
AB 是 圆O 直径
该题中还有哪些面互相垂直
拓展1: 本题中的模型称为鳖膈 (bie nao) 模型,即四个面都是直角三角形的
四面体
C
拓展2: 长方体中的组合体
分析题意,根据题目条件选择 证明哪个面的垂线
恰当的选择方法证明线面垂直 常用方法是线线垂直,则线面 垂直
根据面面垂直的判定定理证明
深化领悟——总结解题步骤
应用判定定理证明平面与平面垂直的基本步骤
定思路
证线面
证面面
转化的思想方法
线线垂直
线面垂直
面面垂直
类比
二面角
特 殊
直二面角
二面角的 平面角
定义面面垂直
归纳小结 — — 构建知识结构
面面垂直的判定定理
数学思想:
符号 语言
图形 语言
文字 语言
平面角
— →
度量
作业1:教科书第159 页练习第4题;
第163页习题8.6第6、7、8题.
作业2:选做1.结合学习过的空间平行关系的判定定理、
性质定理,空间垂直的判定定理,尝试发现其它判定面 面垂直的命题,给出你的结论和证明.
作业布置
作业布置
选做2.“平行关系图谱”已经完成,任意二者间都可以转化,你能 尝试完成“垂直关系图谱”剩余的部分吗
线线平行 线线垂直
面面平行 线面垂直
一个平面经过另一个平
平面内两相交直线分
别平行于另 一个平面
面面垂直
线面平行
普通高中数学 人教版(2019)必修第二册
第八章立体几何初步
8.6.3平面与平面垂直
情景引入
回顾:平面几何中,我们是通过什么概念来刻画两条相交
直线的位置关系
平面内两条直线相交形成4个角, 其中不大于90°的角称为
这两条直线所成的角(或夹角).当两条直线的夹角为时90°,
我们称两直线垂直.
情景引入
如何去刻画两个相交平面的位置关系
探究新知——二面角
类比直线间的夹角,引入二面角的概念:
如图,从一条直线出发的两个半平面所组成的图形叫做二面角.
这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
半平面 半平面
直线将平面分成两
部分,每一部分叫
半平面 .
平面角由射线--点--射线构成 二面角由半平面--棱--半平面构成。
记作:
记作:∠AOB AB-
P Q
-
P
-A
0
-
二面角的记法:
. Q B
l .P 印
C
A
探究新知
角的记法:
o<
二面角
A
B
探究新知——二面角
你能举出生活中常见的二面角吗
O
如何去度量二面角大小
O
观察探究
我们常说:“把门开大一些”,是指哪个角大一些
B
探究新知——二面角的平面角
二面角的平面角的定义
在二面角α-l-β 的棱上任取一
点O,以点O 为垂足,在半平面α和β内
分别作垂直于棱l 的射线OA和OB, 则
射线OA和OB构成的∠AOB叫做二面
角的平面角. 0 ∈l 空间角平面化
OA⊥1
OB⊥1=∠AOB 为二面角α-I- 的平面角
OBcp
符号语言
在棱上选多个点,画出多个所折二面角
的一个平面角,这些角相等吗
你能用某个定理解释为什么
这些角都是相等的吗
A
课后实验:同学们可以自己动手画 出若干个折纸所形成二面角的平面 角,比较它们的大小.
探究新知——二面角的平面角
B C
D
Q
P
二面角的大小可以用其平面角来度量,
二面角的平面角是多少度,
就说这个二面角是多少度.
探究新知——二面角的平面角
想一想:二面角平面角的取值范围是
[0,π]
10
平面角是直角的二面角叫做直二面角.
探究新知——直二面角
探究新知——面面垂直定义
两平面垂直的定义:
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这
如下图,画两个互相垂直的平面时,通常把表示平面的两个平行
两个平面互相垂直.平面α与β垂直,记作α⊥β.
四边形的一组边画成垂直.
探究新知——面面垂直判定定理
实例1 发现:线面垂直,则面面垂直
建筑工人砌墙时,如何
使所砌的墙和水平面垂
直
探索定理
实例2
一扇门在打开的过程中,门所在平 面和水平地面是否始终垂直
你能根据这些实例归纳总结出判定
面面垂直所需的条件吗
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
符号表示: aLβ,aca=aLβ
探究新知——面面垂直判定定理
简记:线面垂直,则面面垂直
探究新知—— 面面垂直判定定理
A
想一想 :
怎么证明面面垂直 的判定定理
C
β
α
B
文字语言 图形语言
符号语言
一个平面过 另一个平面的 垂线,则这两 个平面垂直.
c=aL
探究新知—— 面面垂直判定定理
平面与平面垂直的判定定理
例题讲解——新知应用
例7 如图,在正方体ABCD-A'B'C'D 中,求证平面A'BD⊥ 平面ACC'A'.
例题讲解——新知应用
例7 如图,在正方体ABCD-A'B'C'D 中,求证平面A'BD⊥ 平 面ACC'A'.
证明:∵ABCD-A'B'C'D '是正方体,
∴AA'⊥ 平面ABCD
∴AA'⊥BD,
又BDIAC, 且AA'∩AC=A,
∴BD⊥ 平 面ACC'A',
又BDc 平面A'BD,
∴平面A'BD⊥平面ACC'A'.
C
例题讲解——新知应用
例8 如图,AB 是圆O 的直径,PA 垂直于⊙O 所在的平面,
B
A ∈ 0
本质:线⊥面 面⊥面
关键:在一个平面内找另一个平面的垂线
图中还有哪些平
面是互相垂直的
呢
o 面PAC⊥ 面ABC 面PAB⊥ 面ABC
C是圆周上不同于A,B 的任意一点,
求证:平面PAC⊥平 面PBC. P
BC⊥ 面PAC
业
平面PAC⊥平面PBC
业
BC⊥AC BCLPA
PA⊥面ABC
BCc 面ABC
AB 是 圆O 直径
该题中还有哪些面互相垂直
拓展1: 本题中的模型称为鳖膈 (bie nao) 模型,即四个面都是直角三角形的
四面体
C
拓展2: 长方体中的组合体
分析题意,根据题目条件选择 证明哪个面的垂线
恰当的选择方法证明线面垂直 常用方法是线线垂直,则线面 垂直
根据面面垂直的判定定理证明
深化领悟——总结解题步骤
应用判定定理证明平面与平面垂直的基本步骤
定思路
证线面
证面面
转化的思想方法
线线垂直
线面垂直
面面垂直
类比
二面角
特 殊
直二面角
二面角的 平面角
定义面面垂直
归纳小结 — — 构建知识结构
面面垂直的判定定理
数学思想:
符号 语言
图形 语言
文字 语言
平面角
— →
度量
作业1:教科书第159 页练习第4题;
第163页习题8.6第6、7、8题.
作业2:选做1.结合学习过的空间平行关系的判定定理、
性质定理,空间垂直的判定定理,尝试发现其它判定面 面垂直的命题,给出你的结论和证明.
作业布置
作业布置
选做2.“平行关系图谱”已经完成,任意二者间都可以转化,你能 尝试完成“垂直关系图谱”剩余的部分吗
线线平行 线线垂直
面面平行 线面垂直
一个平面经过另一个平
平面内两相交直线分
别平行于另 一个平面
面面垂直
线面平行
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
