〖数学〗8.4.1平面 教学课件(共29张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修二
文档属性
| 名称 | 〖数学〗8.4.1平面 教学课件(共29张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修二 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:24:36 | ||
图片预览







文档简介
(共29张PPT)
第八章立体几何初步
8.4.1平面
课本第124页~127页
教学目标
01 借助实物了解平面的概念,理解平面的特点和基本性质(重点)
02 了解3个基本事实和3个推论;(重点)
03 运会用符号表示图形中点、直线、平面之间的位置关系;(重点)
04 能运用平面基本性质证明与判断共线、共面、共点问题. (重点、难点)
2
学科素养
了解平面的概念,理解平面的特点和基本性质
能运用平面基本性质证明与判断共线、共面、共点问题
了解3个基本事实和3个推论
数学抽象
逻辑推理
3
前面我们学习了基本几何体,学习了它们的结构特征、平面表示、
面积和体积的计算.在学习棱柱、棱锥、棱台等多面体的过程中,我 们知道顶点、棱、平面多边形等是构成这些多面体的基本元素,这些 元素之间的相互关系,反映了这些多面体的结构特征.实际上,立体 图形都是由点、直线、平面等基本元素组成的,要研究立体图形的结 构特征,就要研究这些基本元素之间的位置关系,我们先从认识点、
直线、平面这些基本元素开始.
4
立体图形都是由点、直线、平面等基本元素组
成的,要研究立体图形的结构特征,就要研究 这些基本元素之间的位置关系,我们先从认识 点、直线、平面这些基本元素开始.
5
S
上底面
D' C' 侧面
A' 入 B
D C
A B 顶点
S 顶点
侧面
侧棱
D
底面 ·
B
E
面
棱
A D
C
B
顶点
F
E D
C
A B
C'
A ' B
顶点二 -F
下底面
侧 棱
底 面
侧面
E' D'
F'
C
现实事物抽象得到的
点A 直线l 不加定义的几何概念
对于本节要学习的“平面”,可以从生活中哪些物体抽象得到呢 平面有什么特点和性质呢
12分钟时间阅读教材P124--127, 完成导纲一、二部分并找到以下问题答案:
(1)生活中哪些物体给你以平面的感觉 平面有什么特点 如何表示平面
(2)点、直线、平面之间有哪些基本位置关系 如何用数学符号表示
(3)平面的性质(3个基本事实及推论)是什么
6分钟时间讨论导纲一、二部分自己未解决的问题
6
们以平面的直观感觉.几何里所说的“平面(plane)” 就是从这样的
一些物体中抽象出来的.
“平 面”与点和直线一样, 都是现实事物抽象得到 的,是不加定义的几何 概念
(1)生活中哪些物体给你以平面的感觉 平面有什么特点 如何表示平面
生活中有一些物体:如课桌面、黑板面、平静的水面等都给我
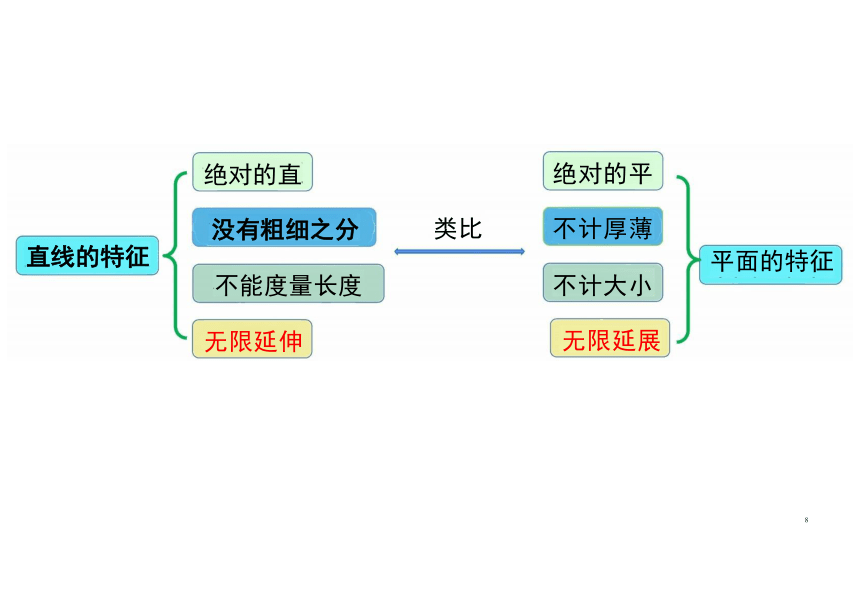
平面的描述与特征
7
绝对的直
没有粗细之分
平面的特征
不能度量长度
无限延伸
绝对的平
不计厚薄
不计大小
无限延展
直线的特征
类比
8
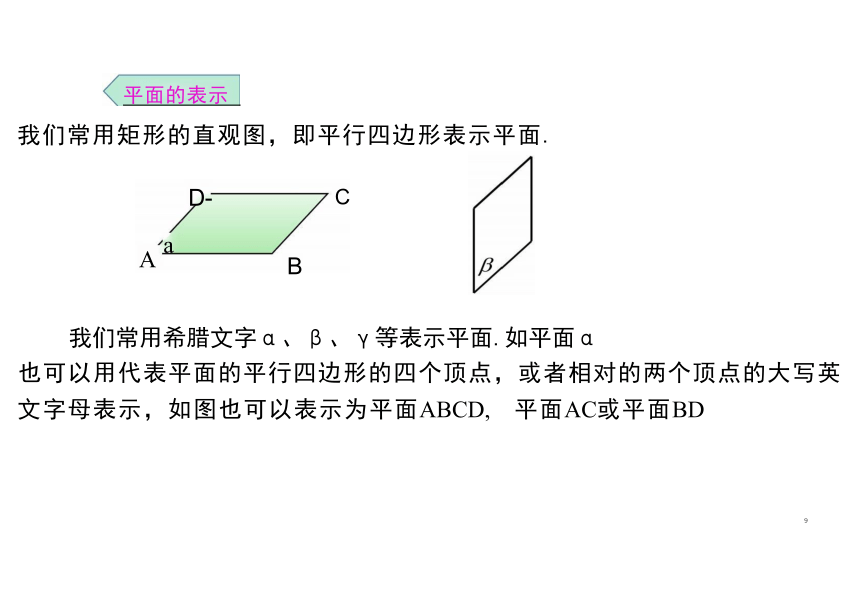
我们常用希腊文字α、β、γ等表示平面.如平面α
也可以用代表平面的平行四边形的四个顶点,或者相对的两个顶点的大写英
文字母表示,如图也可以表示为平面ABCD, 平面AC或平面BD
我们常用矩形的直观图,即平行四边形表示平面.
D-
A a
C
B
平面的表示
9
在画两个平面相交时,一定要画出交线,如果其中一个平面的一部分
被另一个平面挡住,通常把被挡住的部分画成虚线或不画,这样可使画出 的图形立体感更强一些,如图.
两相交平面的画法
α α
A A
β B
B
β
10
【练习】判断下列各题的说法正确与否 1.一个平面长4米,宽2米;
(X)
2.平面上一条直线可以把这个平面分成两部分;
( √)
3.10个平面叠在一起要比一个平面厚;
(×)
4.菱形的面积可以等于4cm ;
( √)
5.一个平面可以把空间分成两部分.
( √)
11
直线上有无数个点,平面内有无数个点,直线、平面都可以看出是点的
集合.接下来我们通过元素与集合、集合与集合之间的关系,分别用文字语 言、符号语音、图形语言来描述,点A, 直线l,m、 平面α的位置关系.
文字语言
A 在1上
A在1外
A 在α内
A在α外
符号语言
AEl
A∈l
AEα
AEα
图形语言
A
A .
点、直线、平面之间的位置关系
A
α
α
L
L
A.
2
3
4
14
—
点、直线、平面之间的位置关系
文字语言 符号语言
5 l,m平行 l//m
6 l,m 相交于A ln m=A
7 l在α内 lcα
8 l不在α内 ldα
9 α平行β a//β
10 a,β 相交于直线l aNβ=l
图形语言
T
m
m
α
l
α
α
β
β
α
l
l
α
A
L
l
基本 事实 基 本 事 实 1 基 本 事 实 2 基 本 事 实 3 文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内 如果两个不重合的平面有一个 公共点,那么它们有且只有一 条过该点的公共直线 图形 语言 ●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, β∈ α,C∈a A∈l,B∈l,且A∈ B∈α→lcα α, P∈α,且P∈ β→ α 且P∈l
∩β=l,
实是人们经过长期观察 也是我们进一步研究立 与实践总结出来的,是几何 体图形的基础。
这三个基本事
推理的基本依据,
平面的基本性质
点 评
平面的基本性质 基本事实1 过不在一条直线上的三点,有且只有一个平面. “不共线三点确定一个平面” a A●
●B
●C
符号表示为CfAB → 有且只有一个平面α, A∈a,B∈a,C∈a.
17
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个
平面内.
符号表示为 A∈l,B∈l, 且A∈α,B∈α → lca.
如果一根直尺边缘上的任意两点在桌面上,
那么直尺的整个边缘就落在了桌面上. A
刻画 a
直线的“直” 平面的“平”
直线的“无限延伸” 刻画 平面的“无限延展”
平面的的基本性质
藻
B
18
点评
符号表示为 P∈a, 且P∈β= a∩β=l, 且P∈1.
如果两个平面有一个公
共点,那么这两个平面一定
相交于过这个公共点的一条
直线.两个平面相交成一条
直线的事实,可以让我们进
一步认识了平面的“平”和
“无限延展”.
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条 过该点的公共直线.
平面的的基本性质
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内 ②判定点是否在面内
①判定两平面相交
②判断点是否在直线上
平面的基本性质
a
推论二 经过两条相交直线,有且只有一个平面.
推论三 经过两条平行直线,有且只有一个平面.
b
C
a
利用基本事实1和2再结合“两点确定一条直线”,可得到下面三个关于确定
一个平面的推论:
推论一 经过一条直线和直线外一点,有且只有一个平面./ A.
B a C
22
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内
①判定两平面相交
②判定点线共面 ②判定点是否在面内
②判断点是否在直线上
平面的基本性质
下列命题正确的是( )
A. 经过三点确定一个平面; B. 经过一条直线和一个点确定一个平面;
C. 两两相交且不共点的三条直线确定一个平面; D. 四边形确定一个平面 .
【解析】A, 当三点共线时不能确定一个平面,故A错误;
B, 点在直线上时不能确定一个平面,故B错误;
C, 由右图可知, C正确: (详解见下页) l A l l
D, 空间四边形不能确定一个平面,故D错误; a
综上知选C
24
1.判断正误. (在题后括号内打“ √ ”或“×”)
(1)一条直线和一个点可以确定一个平面. (
(2)四边形是平面图形. (
(3)两条相交直线可以确定一个平面.(y)
(4)4个平面重叠起来要比一个平面厚.
25
2. 下列结论中不正确的是(D)
A. 若两个平面有一个公共点,则它们有无数个公共点
B. 梯形可确定一个平面
C. 若点A 既在平面α内,又在平面β内,则α与β相交于b, 且点A 在b上
D. 任意两条直线不能确定一个平面
26
3.不重合的三条直线,若相交于一点,最多能确定 3 个平面.
4.四点可以确定 个平面.
1或4或无数
P
A
B
C
27
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内
①判定两平面相交
②判定点线共面 ②判定点是否在面内
②判断点是否在直线上
平面的基本性质
α
证 明 : 因 为I Nl =A, 所 以l 和 l 确定 一 个平面α . (推论1)
因 为L Nl =B, 所 以B∈l .
又 因 为l Ca, 所 以B∈a. (点在线上,线在面内,则点在面内)
同 理 可 证C∈a
又 因 为B∈l ,C∈l , 所 以l Ca. (基本事实2)
所 以 直 线l 、l 、l 在 同 一 平 面 内 .
已 知 : 如 图 所 示 ,l Nl =A,L Nl =B,l Nl =C.
求 证 : 直 线l 、l 、l 在同 一 平面内 .
【练习】证明两两相交且不共点的三条直线在同 一 平面内 .
l Ali
l
29
基本事实1 过不在一条直线上的三点,有且只有一个平面.
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实2用符号表示为 A∈l,B∈l, 且A∈a,B∈a→lca.
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的
公共直线.
基本事实3用符号表示为 P∈α, 且P∈β→a∩β=l, 且P∈1.
基本事实1和2的三个推论:
推论一 经过一条直线和直线外一点,有且只有一个平面.
推论二 经过两条相交直线,有且只有一个平面.
推论三 经过两条平行直线,有且只有一个平面.
30
1.用符号表示下列语句,并画出相应的图形:
( 1 ) 点A在平面α内,点B在平面α外;
(2)直线a经过平面α外的一点M;
(3)直线a既在平面α内,又在平面β内.
2.已知直线b//c, 且直线a与b,c 都相交,求证:直线a,b,c 共面.
31
第八章立体几何初步
8.4.1平面
课本第124页~127页
教学目标
01 借助实物了解平面的概念,理解平面的特点和基本性质(重点)
02 了解3个基本事实和3个推论;(重点)
03 运会用符号表示图形中点、直线、平面之间的位置关系;(重点)
04 能运用平面基本性质证明与判断共线、共面、共点问题. (重点、难点)
2
学科素养
了解平面的概念,理解平面的特点和基本性质
能运用平面基本性质证明与判断共线、共面、共点问题
了解3个基本事实和3个推论
数学抽象
逻辑推理
3
前面我们学习了基本几何体,学习了它们的结构特征、平面表示、
面积和体积的计算.在学习棱柱、棱锥、棱台等多面体的过程中,我 们知道顶点、棱、平面多边形等是构成这些多面体的基本元素,这些 元素之间的相互关系,反映了这些多面体的结构特征.实际上,立体 图形都是由点、直线、平面等基本元素组成的,要研究立体图形的结 构特征,就要研究这些基本元素之间的位置关系,我们先从认识点、
直线、平面这些基本元素开始.
4
立体图形都是由点、直线、平面等基本元素组
成的,要研究立体图形的结构特征,就要研究 这些基本元素之间的位置关系,我们先从认识 点、直线、平面这些基本元素开始.
5
S
上底面
D' C' 侧面
A' 入 B
D C
A B 顶点
S 顶点
侧面
侧棱
D
底面 ·
B
E
面
棱
A D
C
B
顶点
F
E D
C
A B
C'
A ' B
顶点二 -F
下底面
侧 棱
底 面
侧面
E' D'
F'
C
现实事物抽象得到的
点A 直线l 不加定义的几何概念
对于本节要学习的“平面”,可以从生活中哪些物体抽象得到呢 平面有什么特点和性质呢
12分钟时间阅读教材P124--127, 完成导纲一、二部分并找到以下问题答案:
(1)生活中哪些物体给你以平面的感觉 平面有什么特点 如何表示平面
(2)点、直线、平面之间有哪些基本位置关系 如何用数学符号表示
(3)平面的性质(3个基本事实及推论)是什么
6分钟时间讨论导纲一、二部分自己未解决的问题
6
们以平面的直观感觉.几何里所说的“平面(plane)” 就是从这样的
一些物体中抽象出来的.
“平 面”与点和直线一样, 都是现实事物抽象得到 的,是不加定义的几何 概念
(1)生活中哪些物体给你以平面的感觉 平面有什么特点 如何表示平面
生活中有一些物体:如课桌面、黑板面、平静的水面等都给我
平面的描述与特征
7
绝对的直
没有粗细之分
平面的特征
不能度量长度
无限延伸
绝对的平
不计厚薄
不计大小
无限延展
直线的特征
类比
8
我们常用希腊文字α、β、γ等表示平面.如平面α
也可以用代表平面的平行四边形的四个顶点,或者相对的两个顶点的大写英
文字母表示,如图也可以表示为平面ABCD, 平面AC或平面BD
我们常用矩形的直观图,即平行四边形表示平面.
D-
A a
C
B
平面的表示
9
在画两个平面相交时,一定要画出交线,如果其中一个平面的一部分
被另一个平面挡住,通常把被挡住的部分画成虚线或不画,这样可使画出 的图形立体感更强一些,如图.
两相交平面的画法
α α
A A
β B
B
β
10
【练习】判断下列各题的说法正确与否 1.一个平面长4米,宽2米;
(X)
2.平面上一条直线可以把这个平面分成两部分;
( √)
3.10个平面叠在一起要比一个平面厚;
(×)
4.菱形的面积可以等于4cm ;
( √)
5.一个平面可以把空间分成两部分.
( √)
11
直线上有无数个点,平面内有无数个点,直线、平面都可以看出是点的
集合.接下来我们通过元素与集合、集合与集合之间的关系,分别用文字语 言、符号语音、图形语言来描述,点A, 直线l,m、 平面α的位置关系.
文字语言
A 在1上
A在1外
A 在α内
A在α外
符号语言
AEl
A∈l
AEα
AEα
图形语言
A
A .
点、直线、平面之间的位置关系
A
α
α
L
L
A.
2
3
4
14
—
点、直线、平面之间的位置关系
文字语言 符号语言
5 l,m平行 l//m
6 l,m 相交于A ln m=A
7 l在α内 lcα
8 l不在α内 ldα
9 α平行β a//β
10 a,β 相交于直线l aNβ=l
图形语言
T
m
m
α
l
α
α
β
β
α
l
l
α
A
L
l
基本 事实 基 本 事 实 1 基 本 事 实 2 基 本 事 实 3 文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内 如果两个不重合的平面有一个 公共点,那么它们有且只有一 条过该点的公共直线 图形 语言 ●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, β∈ α,C∈a A∈l,B∈l,且A∈ B∈α→lcα α, P∈α,且P∈ β→ α 且P∈l
∩β=l,
实是人们经过长期观察 也是我们进一步研究立 与实践总结出来的,是几何 体图形的基础。
这三个基本事
推理的基本依据,
平面的基本性质
点 评
平面的基本性质 基本事实1 过不在一条直线上的三点,有且只有一个平面. “不共线三点确定一个平面” a A●
●B
●C
符号表示为CfAB → 有且只有一个平面α, A∈a,B∈a,C∈a.
17
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个
平面内.
符号表示为 A∈l,B∈l, 且A∈α,B∈α → lca.
如果一根直尺边缘上的任意两点在桌面上,
那么直尺的整个边缘就落在了桌面上. A
刻画 a
直线的“直” 平面的“平”
直线的“无限延伸” 刻画 平面的“无限延展”
平面的的基本性质
藻
B
18
点评
符号表示为 P∈a, 且P∈β= a∩β=l, 且P∈1.
如果两个平面有一个公
共点,那么这两个平面一定
相交于过这个公共点的一条
直线.两个平面相交成一条
直线的事实,可以让我们进
一步认识了平面的“平”和
“无限延展”.
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条 过该点的公共直线.
平面的的基本性质
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内 ②判定点是否在面内
①判定两平面相交
②判断点是否在直线上
平面的基本性质
a
推论二 经过两条相交直线,有且只有一个平面.
推论三 经过两条平行直线,有且只有一个平面.
b
C
a
利用基本事实1和2再结合“两点确定一条直线”,可得到下面三个关于确定
一个平面的推论:
推论一 经过一条直线和直线外一点,有且只有一个平面./ A.
B a C
22
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内
①判定两平面相交
②判定点线共面 ②判定点是否在面内
②判断点是否在直线上
平面的基本性质
下列命题正确的是( )
A. 经过三点确定一个平面; B. 经过一条直线和一个点确定一个平面;
C. 两两相交且不共点的三条直线确定一个平面; D. 四边形确定一个平面 .
【解析】A, 当三点共线时不能确定一个平面,故A错误;
B, 点在直线上时不能确定一个平面,故B错误;
C, 由右图可知, C正确: (详解见下页) l A l l
D, 空间四边形不能确定一个平面,故D错误; a
综上知选C
24
1.判断正误. (在题后括号内打“ √ ”或“×”)
(1)一条直线和一个点可以确定一个平面. (
(2)四边形是平面图形. (
(3)两条相交直线可以确定一个平面.(y)
(4)4个平面重叠起来要比一个平面厚.
25
2. 下列结论中不正确的是(D)
A. 若两个平面有一个公共点,则它们有无数个公共点
B. 梯形可确定一个平面
C. 若点A 既在平面α内,又在平面β内,则α与β相交于b, 且点A 在b上
D. 任意两条直线不能确定一个平面
26
3.不重合的三条直线,若相交于一点,最多能确定 3 个平面.
4.四点可以确定 个平面.
1或4或无数
P
A
B
C
27
基本 事实 基 本 事 实 1 基 本 事 实 2
基 本 事 实 3
文字 语言 过不在一条直线上的 三点,有且只有一个 平面 如果一条直线上的两个 点在一个平面内,那么 这条直线在这个平面内
如果两个不重合的平面有一个
公共点,那么它们有且只有一 条过该点的公共直线
图形 语言
●B a A° C 符号 语言 CfAB→有且只有一 个平面α,A∈α, B∈α,C∈α A∈l,B∈l,且A∈α, B∈α→lcα
P∈α,且P∈ β→ α∩β=l, 且P∈l
作用 ①确定一个平面的依据 ①判断直线是否在面内
①判定两平面相交
②判定点线共面 ②判定点是否在面内
②判断点是否在直线上
平面的基本性质
α
证 明 : 因 为I Nl =A, 所 以l 和 l 确定 一 个平面α . (推论1)
因 为L Nl =B, 所 以B∈l .
又 因 为l Ca, 所 以B∈a. (点在线上,线在面内,则点在面内)
同 理 可 证C∈a
又 因 为B∈l ,C∈l , 所 以l Ca. (基本事实2)
所 以 直 线l 、l 、l 在 同 一 平 面 内 .
已 知 : 如 图 所 示 ,l Nl =A,L Nl =B,l Nl =C.
求 证 : 直 线l 、l 、l 在同 一 平面内 .
【练习】证明两两相交且不共点的三条直线在同 一 平面内 .
l Ali
l
29
基本事实1 过不在一条直线上的三点,有且只有一个平面.
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实2用符号表示为 A∈l,B∈l, 且A∈a,B∈a→lca.
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的
公共直线.
基本事实3用符号表示为 P∈α, 且P∈β→a∩β=l, 且P∈1.
基本事实1和2的三个推论:
推论一 经过一条直线和直线外一点,有且只有一个平面.
推论二 经过两条相交直线,有且只有一个平面.
推论三 经过两条平行直线,有且只有一个平面.
30
1.用符号表示下列语句,并画出相应的图形:
( 1 ) 点A在平面α内,点B在平面α外;
(2)直线a经过平面α外的一点M;
(3)直线a既在平面α内,又在平面β内.
2.已知直线b//c, 且直线a与b,c 都相交,求证:直线a,b,c 共面.
31
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
